粒子群优化 (Particle Swarm Optimization, PSO) 算法是由Eberhart和Kennedy于1995年提出的一种通过模拟鸟群觅食行为而发展起来的随机搜索算法[1-2]。PSO算法没有过多需要调节的参数,因而简单易行,目前已广泛应用于各类约束优化[3-4]、数据挖掘[5],以及工程应用[6-8]等领域。
在标准粒子群优化算法中,粒子的更新仅仅与种群的最优粒子和自身的历史最优值有关,这种粒子更新机制导致大量的种群进化信息被浪费,Chen等[9]提出生命周期和领导年龄的概念,当一个粒子已经长时间领导群体的进化方向时,允许其他粒子取代其领导地位。Shi等[10]提出惯性权重的概念,有效调节了上一时刻粒子速度对进化过程的影响程度。惯性权重是一种调节群的全局探索和局部挖掘能力的机制, 惯性权重ω通过控制之前的速度来调节粒子的冲力。文献[11]提出了一种负反馈系统,该系统由多样性控制器 (Diversity Controller)、微粒群优化器 (PSO Optimizer) 和微粒群体 (Swarm) 三部分组成,根据种群的多样性来调整惯性权重。汤可宗等[12]从几何角度提出中心概念,文献[13]将扰动策略和变异运算引入PSO,一定程度上增加了群体多样性,从而减小算法陷入局部最优的可能。刘朝华等[14]提出了一种双态免疫微粒群算法,将微粒群分为捕食和探索两种状态,同时引入免疫克隆选择和受体编辑机制,增强了群体逃离局部最优的能力。邱飞岳等[15]引入了随即变量分解策略,将合作协同进化框架融合于多目标粒子群优化算法,最后用加法二进制ε指标、超体积指标 (HyperVolume, HV) 和算法运行时间对算法性能进行分析,实验结果表明该算法可以有效解决多目标粒子群算法在大规模变量方面的缺陷,并在求解精度和运行效率上有显著提升,但是依然存在陷入局部最优的缺陷。
以上的改进策略一定程度上提高了粒子群算法的性能, 但是如果单纯地用质心去替换种群最优粒子,会大大降低种群多样性; 改变惯性权重和施加扰动操作的确是会对增加种群多样性有一定帮助, 但同时也会降低种群的收敛速度。
本文通过对柯西变异算法和基于质心的粒子群算法的研究和改进,提出了一种结合质心思想和柯西变异策略的粒子群优化算法 (Centroid and Cauchy Mutation Particle Swarm Optimization, CCMPSO)。该算法在初始化阶段采用Logistic混沌初始化策略,惯性权重根据种群多样性进行自适应调整,引入质心的思想,计算个体极值质心和种群质心,将其添加到粒子的速度更新公式中,使用柯西变异策略,对全局最优施加变异操作。仿真实验结果表明该算法的收敛速度和寻优能力要优于PSO和许多改进PSO。
1 粒子群算法标准粒子群算法是一种群体智能算法,群体中的每个成员被称为粒子,在搜索空间中以一定的速度寻找最优值。每个粒子根据个体极值pbest和全局极值gbest来更新自己的位置和速度。设在D维搜索空间中,一个大小为N的种群,其中第i个粒子的速度矢量可以表示为Vi={Vi1, Vi2, …,ViD},位置矢量可以表示为Xi={Xi1, Xi2, …,XiD},第i个粒子到目前为止所找到的最优位置计为pbesti={pbesti1, pbesti2, …,pbestiD},整个种群找到的最优位置计为gbest={gbest1, gbest2, …,gbestD},粒子xi的位置和速度更新公式如下:
| $ {\boldsymbol{V}}_{ij}^{t + 1} = {\boldsymbol{V}}_{ij}^t + {c_1}{r_1}({\boldsymbol{pbest}}_{ij}^t-{\boldsymbol{X}}_{ij}^t) + {c_2}{r_2}({\boldsymbol{gbest}}_j^t-{\boldsymbol{X}}_{ij}^t) $ | (1) |
| $ {\boldsymbol{X}}_{ij}^{t + 1} = {\boldsymbol{X}}_{ij}^t + {\boldsymbol{V}}_{ij}^{t + 1} $ | (2) |
其中:i=1, 2, …, N,j=1, 2, …,D,N 为种群规模,D为搜索空间的维数;c1、c2为学习因子; t为当前迭代次数;r1、r2是[0, 1]的随机数;为了避免粒子飞出搜索空间,速度Vij通常被限制在某个搜索区域内[-Vmax, Vmax]。
从式 (1) 可以看出,粒子群具有自我总结和向全局最优个体学习的能力,粒子的速度更新公式主要受三方面因素的影响:第一部分为上一时刻的速度,作为之前搜索方向的记忆;第二部分为认知分量,它模拟了该粒子最好位置的记忆;第三部分称为社会分量,它刻画了个体试图达到的标准,对粒子的速度更新具有重要影响。即在迭代过程中逐步向自己的历史最优pbest和种群的全局最优gbest靠近。c1调节粒子飞向pbest的步长,c2调节粒子飞向gbest的步长,共同引导粒子飞向粒子群中的最好位置。
在粒子群优化算法中,由于粒子的速度和方向受到gbest的极大影响,如果当前种群所找到的最优解只是整个搜索空间中的局部极值,那算法将会陷入局部最优,寻优效果大大降低;并且粒子仅依赖于个体最优和全局最优将导致粒子无法从其他的较优粒子那里获得搜索信息,大量的种群搜索信息被浪费。
2 相关研究 2.1 Logistic映射粒子群优化算法文献[16]在PSO粒子初始化的阶段引入了混沌序列来提高初始种群的质量,并对陷入局部最优的粒子实行差分变异操作。混沌状态类似于随机运动,混沌具有遍历性、随机性和规律性等特点。依靠混沌映射序列对粒子的速度和位置进行初始化,不仅保证了粒子的随机性,而且使得初始粒子因为混沌的遍历性而具有多样性的特点,达到在搜索空间中均匀分布的效果。Logistic映射粒子群优化 (Logistic Map Particle Swarm Optimization, LMPSO) 算法根据Logistic映射形式得到混沌序列yn+1, j,然后映射到搜索区间[aj, bj]:
| $ x_{n, j} = {a_j} + ({b_j}-{a_j}) \times {y_{n, j}} $ | (3) |
其中:j=1, 2, …,D,xn即为种群的一个可行解,粒子速度的初始化方法和位置的初始化方法一样,只是将变量的取值范围改为速度的限定范围。
2.2 质心粒子群优化算法汪永生等[17]从物理角度提出质心概念,根据所有粒子的个体最优记录计算出质心,将其与全局最优记录进行比较和替换,更新全局最优;同时还提出了质心粒子群优化 (Centroid Particle Swarm Optimization, CPSO) 算法,通过计算出的质心,引导粒子更快地飞向最优位置,有效提高了算法的收敛速度,但是种群的多样性会下降较快,算法容易陷入局部最优。
2.3 柯西变异粒子群优化算法文献[18]将柯西变异操作加入到粒子群算法当中,康岚兰等提出,在基本PSO算法收敛之前,全局极值gbest的搜索空间具有局限性,总是徘徊于几个候选解之间,如果加大gbest的搜素范围,将有效降低陷入局部最优和过早收敛的可能。其柯西变异策略为:
| $ gbes{t^*}(i) = gbest(i) + u(i) \cdot F(xm) $ | (4) |
式中:u(i) 是各维变异权重的平均值,F(xm) 是标准柯西分布函数。
2.4 CCMPSO本文提出的CCMPSO算法是结合了质心思想、柯西变异和混沌初始化的综合优化算法,并对惯性权重实施动态调整策略。在算法的初始化阶段,使用Logistic混沌映射产生初始种群,按照如下方程进行反复迭代:
| $ x(t + 1) = \mu x(t)(1-x(t)) $ | (5) |
其中:t为时间步,又称迭代次数;x代表一个粒子及搜索空间中的一个可行解;μ为调节参数。首先在 (0, 1) 随机产生一个D维的基准粒子y0,y0=(y01, y02, …,y0D), 将此粒子作为Logistic映射的初始迭代粒子,根据Logistic映射的形式,得到混沌序列xn+1, j,即:
| $ {y_{n + 1, j}} = \mu {y_{n, j}}(1-{y_{n, j}});n = 0, 1, 2, \cdots, N, j = 1, 2, \cdots, D $ | (6) |
然后,将粒子根据式 (5) 映射到搜索空间[-R, R]中:
| $ x_{n + 1, j} = R \times (2 \times {y_{n + 1, j}}-1) $ | (7) |
其中:n=0, 1, 2, …, N, j=1, 2, …, D,这样就产生了N个D 维的粒子,对应搜索空间中的 N 个可行解,即构成算法的初始种群。同样,粒子的速度初始化类似于位置初始化,只不过将搜索空间改为粒子的速度限定值[Vmin, Vmax]。
惯性权重方面采用依据种群多样性动态改变的策略,首先计算群体多样性:
| $ dis = \frac{1}{{N \cdot L}}\sum\limits_{i = 1}^N {\sqrt {\sum\limits_{j = 1}^D {{{({x_{ij}}-{p_j})}^2}} } } $ | (8) |
其中: N为种群规模,D为粒子维数,pj为种群的质心,L 是搜索空间最大对角距离。阈值为:
| $ dis' = a(1-\frac{t}{{b \cdot T}}) $ | (9) |
其中:T为最大迭代次数;t 是当前迭代次数;a和b是调节参数,取值 (0, 1)。
在算法的运行初期,群体多样性较高,粒子搜索到的位置一般较差,种群需要较强的全局寻优能力让粒子去探索更多的位置;在算法运行的后期,种群多样性降低,粒子一般聚集在全局最优的附近,因此种群需要更高的局部挖掘能力来找出最优值。本文使用文献[19]中提出的公式作为调节系数的参考标准:
| $ jd = F(gbest(t))/{F_{{\rm{avg}}}} $ | (10) |
其中:F(gbest(t)) 是全局最优的适应度函数, Favg是平均适应度函数。从式 (10) 中可以看出jd的取值范围是 (0, 1]。
如果dis≤dis′,说明此时的种群多样性较低,需要较高的惯性权重增加粒子全局寻优的能力,所以令:
| $ \omega = {\omega _{\max }}-(\frac{{{\omega _{\max }}-{\omega _{\min }}}}{T}) \cdot t + jd \cdot {\omega _2} $ | (11) |
如果dis > dis′,说明此时的种群多样性较高,需要较低的惯性权重增加粒子局部挖掘能力,所以令:
| $ \omega = {\omega _{\max }}-(\frac{{{\omega _{\max }}-{\omega _{\min }}}}{T}) \cdot t-jd \cdot {\omega _2} $ | (12) |
式中:ωmax是惯性权重的最大值,一般取0.9;ωmin是惯性权重的最小值,一般取0.4;ω2为调节部分,动态改变惯性权重。
本文引入了个体极值质心和种群质心两个抽象粒子,将二者加入到粒子的速度更新公式中,使得粒子在调整自己的飞行方向时,不仅要向个体极值和全局极值学习,还要依赖种群质心和个体极值质心,其中包含了其他粒子提供的信息。此方法在不影响算法精英学习能力的基础上,提高了粒子间相互交流的能力,使得有用的信息得以利用,有效保证了种群的寻优质量。设pbest是粒子xi的历史最优解,N是种群规模,xct是种群的质心,pct是粒子第t次迭代产生的个体最优质心。定义如下:
| $ x_c^t = \frac{1}{N}\sum\limits_{i = 1}^N {x_i^t} $ | (13) |
| $ p_c^t = \frac{1}{N}\sum\limits_{i = 1}^N {p_i^t} $ | (14) |
将式 (13)、(14) 和惯性权重ω引入式 (1) 得到式 (15):
| $ \begin{array}{l} {\boldsymbol{V}}_{ij}^{t + 1} = \omega {\boldsymbol{V}}_{ij}^t + {c_1}{r_1}({\boldsymbol{pbest}}_{ij}^t-{\boldsymbol{X}}_{ij}^t) + {c_2}{r_2}({\boldsymbol{gbest}}_j^t-{\boldsymbol{X}}_{ij}^t) + \\ \;\;\;\;\;\;\;\;\;{c_3}{r_3}(\partial x_{ci}^t + (1-\partial )p_{ci}^t - x_{ij}^t) \end{array} $ | (15) |
其中: ∂是[0, 1]的一个常数,称为权重调节因子;c1、c2、c3是学习因子;r是[0, 1]的随机数。基于式 (14) 和式 (2) 对粒子进行速度更新和位置更新,使得粒子在运动过程中不仅依靠个体最优和全局最优,还要依靠其他粒子的个体最优解和全局最优解,增强了群体内部的信息交流能力, 有效提高了PSO算法的收敛性能。
变异算子包括高斯变异 (Gaussian mutation) 和柯西变异 (Cauchy mutation)[20]。相对于高斯变异算子,柯西分布最大的特点是具有较长的两翼,即产生的随机数的范围更大,使得粒子有更大的几率跳出局部极值[21],同时较低的峰值使得柯西变异操作将花费更少的时间代价来搜索邻近区域。本文的算法采用标准的柯西分布对gbest进行变异操作:
| $ gbest_j^* = gbes{t_j} + \eta \times C(0, 1) $ | (16) |
| $ \eta = {e^{-\lambda \cdot \frac{t}{T}}} $ | (17) |
其中:gbestj是全局最优的第j维分量;η为变异权重,随着迭代次数的增加而减小;λ是常数,本文中取10;C(0, 1) 是比例参数t=1的柯西概率分布产生的一个随机数,该方法使得算法在前期发生较大程度的变异,在后期发生较小程度的变异,使得算法既具有收敛能力,又可以避免陷入局部最优。
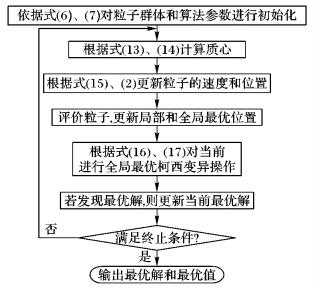
2.5 算法的执行过程算法的流程如图 1所示。图中评价粒子的操作主要是判断粒子在更新过速度和位置之后,是否位于更好的位置,如果是,则将其设置为粒子的个体最优;同样判断种群中的全局最优是否发生了改变,如果是,则更新全局最优。
|
图 1 算法流程 Figure 1 Flow of the algorithm |
本文使用表 1中的7个基准测试函数来测试本文提出的CCMPSO算法性能,其中:f1、f2是单峰函数,f3~f7是多峰函数,对每个函数独立运行20次,对运行后的最优结果求出平均值、标准差和最小值。PSO是基本的PSO算法;CPSO是在PSO的基础上增加了群体质心,用来引导粒子的速度进行更新;CMPSO是在PSO的基础上增加了柯西变异的策略,为了增加群体的多样性,使粒子跳出局部最优;LMPSO是引入了混沌初始化的粒子群优化算法,一定程度上提高了初始种群的质量。为了增强可比性,本次实验各算法的种群规模都相同N=30,c1=c2=2,维数D=150。实验的运行环境为Microsoft Windows 7操作系统,Intel CORE i5处理器,4 GB内存,在Matlab R2014b语言环境下编写测试程序。
| 表 1 基准测试函数 Table 1 Benchmark functions |
为了能够更真实地比较各种算法的寻优效果,每个测试函数均在上述条件下运行多次,计算统计结果进行比较 (均值、标准差和最小值),结果如表 2所示。从表 2的实验结果可以看出:本文所提出的综合算法在7个测试函数中得到20个最优值; CPSO和CMPSO各取得2个最优结果; 综合算法CCMPSO在大部分的测试函数上的表现都明显优于PSO和其他几种优化算法,且在函数f2和f5上相比PSO体现出较大优势,特别在f4和f5测试函数上收敛到最小值0。就收敛均值单项而言,CCMPSO均优于本文所列的PSO等其他算法,可见收敛性能较优。就算法运行时间而言,由于CCMPSO算法引入了柯西变异操作和求取质心的操作,所以运行时间相对有所增加,但时间差距一般保持在5 s左右,特别地对于f6和f7函数,因为以上五种算法均迭代2 400次,所以运行时间较长。
| 表 2 各算法仿真结果 Table 2 Simulation results of the algorithms |
表 3是10维和30维运行结果,维数较低时CCMPSO算法的优越性不是特别明显,特别是在f6和f7测试函数的寻优过程中,其收敛结果并不理想。算法的稳定性采用李雅普诺夫稳定性理论进行分析,把全局最优位置Pg、个体最优位置Pi、种群质心Xc、个体极值质心Pc假设为随时间不变的变量,即时不变;而惯性权重ω、认知系数c1、社会系数c2、质心系数c3是线性变化的变量。首先根据式 (15) 和式 (2) 得到CCMPSO的进化方程,如下所示:
| $ \begin{array}{l} {{\boldsymbol{v}}_i}(t + 1) = \omega {{\boldsymbol{v}}_i}(t) + {c_1}{r_1}[{{\boldsymbol{P}}_i}-x_i(t)] + \\ \;\;\;\;\;\;\;{c_2}{r_2}[{\boldsymbol{P}}_g-{\boldsymbol{x}}_i(t)] + {c_3}{r_3}[\partial {\boldsymbol{X}}_c + (1-\partial ){{\boldsymbol{P}}_c}-{{\boldsymbol{x}}_i}(t)] \end{array} $ | (18) |
| $ {{\boldsymbol{x}}_i}(t + 1) = {\boldsymbol{x}}_i(t) + {\boldsymbol{v}}_i(t + 1) $ | (19) |
| 表 3 各算法仿真结果 Table 3 Simulation results of algorithms |
从式 (19) 可以得到:
vi(t+1)=xi(t+1)-xi(t)
将其代入速度进化方程可得:
| $ \begin{array}{l} {{\boldsymbol{x}}_i}(t + 1)- {{\boldsymbol{x}}_i}(t) = \omega [{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)] + \\ \;\;\;\;\;\;{c_1}{r_1}[{{\boldsymbol{P}}_i}-{\boldsymbol{x}}_i(t)] + {c_2}{r_2}[{\boldsymbol{P}}_g-{\boldsymbol{x}}_i(t)] + \\ \;\;\;\;\;\;{c_3}{r_3}[\partial {\boldsymbol{X}}_c + (1-\partial ){{\boldsymbol{P}}_c}-{{\boldsymbol{x}}_i}(t)] \end{array} $ |
将xi(t+1) 作一阶近似,即将xi(t+1)=xi(t)+
| $ \begin{array}{l} \mathop {{{{\boldsymbol{\dot x}}}_i}(t)}\limits = \omega [{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)] + {c_1}{r_1}[{{\boldsymbol{P}}_i}-{\boldsymbol{x}}_i(t)] + \\ \;\;\;\;\;\;\;\;\;\;{c_2}{r_2}[{\boldsymbol{P}}_g-{\boldsymbol{x}}_i(t)] + {c_3}{r_3}[\partial {\boldsymbol{X}}_c + (1-\partial ){{\boldsymbol{P}}_c}-{{\boldsymbol{x}}_i}(t)] \end{array} $ |
设φ1=c1r1, φ2=c2r2, φ3=c3r3, φ=φ1+φ2+φ3,PQ={φ1Pi+φ2Pg+φ3[∂Xc+(1-∂)Pc]}/φ,则:
| $ \begin{array}{l} \mathop {{{{\boldsymbol{\dot x}}}_i}(t)}\limits = \omega [{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)] + \\ \;\;\;\;\;\;\varphi [\frac{{{\varphi _1}{{\boldsymbol{P}}_i} + {\varphi _2}{{\boldsymbol{P}}_g} + {\varphi _3}[\partial {{\boldsymbol{X}}_c} + (1-\partial ){{\boldsymbol{P}}_c}]}}{\varphi } -{{\boldsymbol{x}}_i}(t)] \end{array} $ | (20) |
式 (20) 是CCMPSO算法的控制方程,接下来使用李雅普诺夫第二方法推导算法的稳定性。
取误差变量[22]ei(t)=xi(t)-PQ,并假设PQ保持不变,也就是PQ保持时不变,即
| $ \begin{array}{l} \mathop {{{{\boldsymbol{\dot v}}}_i}(t)}\limits = {[{\boldsymbol{e}}_i(t)]^{\rm{T}}}{{\boldsymbol{e}}_i}(t)\\ \;\;\;\;\;\;\; = {[\mathop {{{{\boldsymbol{\dot x}}}_i}(t)}\limits-\mathop {{{{\boldsymbol{\dot P}}}_Q}}\limits]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}]\\ \;\;\;\;\;\;\; = {[\mathop {{{{\boldsymbol{\dot x}}}_i}(t)}\limits]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}]\\ \;\;\;\;\;\;\; = {\{ \omega [{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)] + \varphi [{{\boldsymbol{P}}_Q}-{{\boldsymbol{x}}_i}(t)]\} ^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}]\\ \;\;\;\;\;\;\; = \omega {[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}] + \varphi {[{{\boldsymbol{P}}_Q}-{{\boldsymbol{x}}_i}(t)]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}]\\ \;\;\;\;\;\;\; = \omega {[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}] - \varphi {[{{\boldsymbol{P}}_Q}-{{\boldsymbol{x}}_i}(t)]^{\rm{T}}}[{{\boldsymbol{P}}_Q}-{{\boldsymbol{x}}_i}(t)]\\ \;\;\;\;\;\;\; = \omega {[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)]^{\rm{T}}}[{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{P}}_Q}] -\varphi ||{{\boldsymbol{P}}_Q} -{{\boldsymbol{x}}_i}(t)|{|^2} \end{array} $ |
因为有任意两个n维向量x=(x1, x2, …,xn)、y=(y1, y2, …,yn),有
| $ {(||{\boldsymbol{x}}||\;\;\;||{\boldsymbol{y}}||)^2}- ({{\boldsymbol{x}}^{\rm{T}}}{\boldsymbol{y}}) = \sum\limits_{i = 1}^n {{x_i}^2} \sum\limits_{i = 1}^n {{y_i}^2}- {[\sum\limits_{i = 1}^n {{x_i}{y_i}}]^2} = \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {({x_i}{y_j} -{x_j}{y_i}) \ge 0} } $ |
可得xTy≤‖x‖‖y‖,因此有:
[xi(t)-xi(t-1)]Tei(t)≤‖xi(t)-xi(t-1)‖T‖ei(t)‖
所以:
| $ \begin{array}{l} \mathop {{{{\boldsymbol{\dot x}}}_i}(t)}\limits \le \omega ||{{\boldsymbol{x}}_i}(t)- {{\boldsymbol{x}}_i}(t- 1)||\;\;||{\boldsymbol{x}}(t)- {{\boldsymbol{P}}_Q}|| - \varphi ||{{\boldsymbol{P}}_Q} - {{\boldsymbol{x}}_i}(t)|{|^2}\\ \; = [\omega ||{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)||-\varphi ||{{\boldsymbol{P}}_Q} - {\boldsymbol{x}}(t)||]||{{\boldsymbol{P}}_Q} -{{\boldsymbol{x}}_i}(t)|| \end{array} $ |
因为‖PQ-xI(t)‖≥0,所以要使
ω‖xi(t)-xi(t-1)‖-φ‖PQ-x(t)‖≤0
即
| $ \left\{ \begin{array}{l} \omega \le \frac{{\varphi ||{{\boldsymbol{P}}_Q}-{{\boldsymbol{x}}_i}(t)||}}{{||{{\boldsymbol{x}}_i}(t)-{{\boldsymbol{x}}_i}(t-1)||}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {{{\boldsymbol{x}}_i}(t) - {{\boldsymbol{x}}_i}(t - 1)} \right\| > 0\\ \omega \in \left\lceil {0, 1} \right\rceil, \;\;\;\;\;\;其他 \end{array} \right. $ |
|
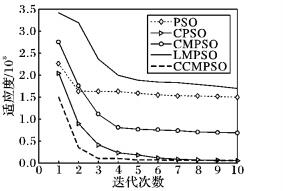
图 2 f1的收敛曲线 Figure 2 Convergence curve of f1 |
|
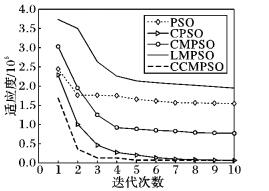
图 3 f2的收敛曲线 Figure 3 Convergence curve of f2 |
|
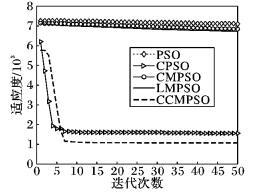
图 4 f3的收敛曲线 Figure 4 Convergence curve of f3 |
|
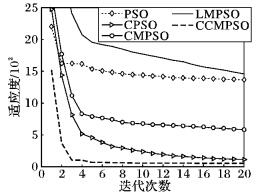
图 5 f4的收敛曲线 Figure 5 Convergence curve of f4 |
|
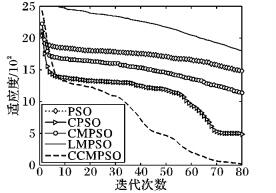
图 6 f5的收敛曲线 Figure 6 Convergence curve of f5 |
|
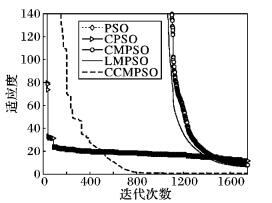
图 7 f6的收敛曲线 Figure 7 Convergence curve of f6 |
|
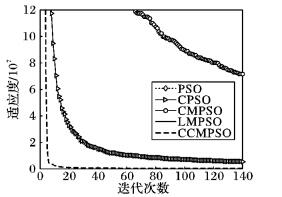
图 8 f7的收敛曲线 Figure 8 Convergence curve of f7 |
从图 2,3,5中可以看出,CCMPSO和CPSO具有较好的寻优能力,可以在规定的迭代次数内收敛到最优值,而且尽管最后收敛精度相差无几,但是CCMPSO的收敛速度要更快于CMPSO。从图 4,7可以看出,对于f3、f6函数,在算法迭代初期,CCMPSO比CPSO稍微逊色,但是CCMPSO的收敛效果在短时间内可以迅速赶上和反超CPSO,最终的收敛精度也要优于后者,具有较好的寻优能力;而PSO、CMPSO和LMPSO则陷入局部最优,导致算法停滞。在图 8中,对于函数f7,CCMPSO算法可以迅速收敛到最优值。通过图 6可以看出,在测试f5函数时CPSO可以在算法前期快速收敛到1 400附近,但是随后会在5~60左右的迭代次数内陷入局部极值,使得算法耗费了大量的时间;而CCMPSO尽管在初期0~20左右的迭代次数内收敛较慢,但是随后可以迅速跳出局部极值,且可以持续保持较快的收敛速度直到寻找到全局最优,最终的收敛精度也优于CPSO;而PSO、CMPSO和LMPSO尽管可以始终保持收敛状态,但是收敛速度和收敛精度相比CCMPSO要逊色很多。
综合实验结果和分析过程,本文提出的CCMPSO算法是一种有效、快速和稳定的PSO改进算法。
从f1~f7的收敛图像中可以明显看出,CCMPSO算法的收敛效果呈现相对较好的态势。除此之外,结合了质心思想的CPSO算法的收敛曲线,始终最靠近CCMPSO的收敛曲线,其次是引入柯西变异策略的CMPSO算法。因此可以得出结论,在结合了质心思想和柯西变异策略的CCMPSO算法中,质心算子对CCMPSO算法的贡献度最高,柯西变异算子次之,混沌初始化算子的贡献度最低。
4 结语本文为解决传统粒子群算法收敛精度不高的问题,提出了一种混合的粒子群优化算法,该算法在融合了质心策略和柯西变异算法的基础上, 引进了Logistic混沌初始化策略,提高了初始种群的质量,并根据种群多样性对惯性权重进行了动态调整,有效平衡了种群的在不同阶段的全局寻优能力和局部挖掘能力。最后在对比测试和实验分析阶段,通过与标准PSO和其他几种改进PSO算法的比较,本算法呈现出较好的仿真结果,算法的收敛精度有了明显提升,通过标准差参数可以说明算法同样具有较高的稳定性,但是依然存在陷入局部最优的可能。进一步的研究工作将主要围绕如何降低算法的时间复杂度以及进一步提高算法的收敛精度方面展开。
| [1] | KENNEDY J, EBERHART R C.Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks. Washington, DC:IEEE Computer Society, 1995:1942-1948. |
| [2] | SHIYH.EBERHART R C.A modified particle swarm optimizer[C]//Proceedings of the 1998 IEEE International Conference on Evolutionary Computation. Piscataway, NJ:IEEE, 1998:67-73. |
| [3] | CAMPOS M, KROHLING R A. Hierarchical bare bones particle swarm for solving constrained optimizationproblems[C]//Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Piscataway, NJ:IEEE, 2013:805-812. |
| [4] | CAMPOS M, KROHLING R A. Bare bones particle swarm with scale mixture of Gaussians for dynamic constrained optimization[C]//Proceedings of the 2014 IEEE Congress on Evolutionary Computation. Piscataway, NJ:IEEE, 2014:202-209. |
| [5] | ZHANG Y, GONG D, HU Y, et al. Feature selection algorithm based on bare bones particle swarm optimization[J]. Neurocomputing, 2015, 148: 150-157. doi: 10.1016/j.neucom.2012.09.049 |
| [6] | 曹春红, 王利民, 赵大哲, 等. 基于小生境改进粒子群算法的几何约束求解[J]. 仪器仪表学报, 2012, 33(9): 2125-2129. ( CAO C H, WANG L M, ZHAO D Z, et al. Geometric constraint solving based on niche improved particle swarm optimization[J]. Chinese Journal of Scientific Instrument, 2012, 33(9): 2125-2129. ) |
| [7] | 唐贤伦, 张衡, 李进, 等. 基于多Agent粒子群优化算法的电力系统经济负荷分配[J]. 电力系统保护与控制, 2012, 40(10): 42-47. ( TANG X L, ZHANG H, LI J, et al. Multiple Agent particle swarm algorithm based economic load distribution in power system[J]. Power System Protection and Control, 2012, 40(10): 42-47. doi: 10.3969/j.issn.1674-3415.2012.10.008 ) |
| [8] | KOSHTI A, ARYA L D, CHOUBE S C. Voltage stability constrained distributed generation planning using modified bare bones particle swarm optimization[J]. Journal of the Institution of Engineers (India) Series B (Electrical, Electronics & Telecommunication and Computer Engineering), 2013, 94(2): 123-133. |
| [9] | CHEN W N, ZHANG J, LIN Y, et al. Particle swarm optimization with an aging leader and challengers[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(2): 241-258. doi: 10.1109/TEVC.2011.2173577 |
| [10] | SHI Y, EBERHART R. A modified particle swarm optimizer[C]//Proceedings of the1998 IEEE Conference on Evolutionary Computation. Piscataway, NJ:IEEE, 1998:69-73. |
| [11] | 介婧, 曾建潮, 韩崇昭. 基于群体多样性反馈控制的自组织微粒群算法[J]. 计算机研究与发展, 2008, 45(3): 464-471. ( JIE J, ZENG J C, HAN C Z. Self-organized particle swarm optimization based on feedback control of diversity[J]. Journal of Computer Research and Development, 2008, 45(3): 464-471. ) |
| [12] | 汤可宗, 柳炳祥, 杨静宇, 等. 双中心粒子群优化算法[J]. 计算机研究与发展, 2012, 49(5): 1086-1094. ( TANG K Z, LIU B X, YANG J Y, et al. Double center particle swarm optimization algorithm[J]. Journal of Computer Research and Development, 2012, 49(5): 1086-1094. ) |
| [13] | 赵新超, 刘国莅, 刘虎球, 等. 基于非均匀变异和多阶段扰动的粒子群优化算法[J]. 计算机学报, 2014, 37(9): 2058-2068. ( ZHAO X C, LIU G L, LIU H Q, et al. Particle swarm optimization algorithm based on non-uniform mutation and multiple stages perturbation[J]. Chinese Journal of Computers, 2014, 37(9): 2058-2068. ) |
| [14] | 刘朝华, 张英杰, 章兢, 等. 一种双态免疫微粒群算法[J]. 控制理论与应用, 2011, 28(1): 65-72. ( LIU C H, ZHANG Y J, ZHANG J, et al. A novel binary-state immune particle swarm optimization algorithm[J]. Control Theory and Applications, 2011, 28(1): 65-72. ) |
| [15] | 邱飞岳, 莫雷平, 江波, 等. 基于大规模变量分解的多目标粒子群优化算法研究[J]. 计算机学报, 2015, 38(12): 2598-2613. ( QIU F Y, MO L P, JIANG B, et al. Multi-objective particle swarm optimization algorithm using large scale variable decomposition[J]. Chinese Journal of Computers, 2015, 38(12): 2598-2613. ) |
| [16] | 刘建平. 基于混沌和差分进化的混合粒子群优化算法[J]. 计算机仿真, 2012, 29(2): 208-212. ( LIU J P. Hybrid particle swarm optimization algorithm based on chaos and differential evolution[J]. Journal of Computer Simulation, 2012, 29(2): 208-212. ) |
| [17] | 汪永生, 李均利. 质心粒子群优化算法[J]. 计算机工程与应用, 2011, 47(3): 34-37. ( WANG Y S, LI J L. Centroid particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2011, 47(3): 34-37. ) |
| [18] | 康岚兰, 董文永, 田降森. 一种自适应柯西变异的反向学习粒子群优化算法[J]. 计算机科学, 2015, 42(10): 226-231. ( KANG L L, DONG W Y, TIAN J S. A novel particle swarm optimization algorithm with adaptive Cauchy mutation[J]. Computer Science, 2015, 42(10): 226-231. ) |
| [19] | 黄泽霞, 俞攸红, 黄德才. 惯性权重自适应调整的量子粒子群优化算法[J]. 上海交通大学学报, 2012, 46(2): 228-232. ( HUANG Z X, YU Y H, HUANG D C. Quantum behaved particle swarm algorithm withself adapting adjustment of inertia weight[J]. Journal of Shanghai Jiao Tong University, 2012, 46(2): 228-232. ) |
| [20] | KROHLING R A, MENDEL E. Bare bones particle swarm optimization with Gaussian or Cauchy jumps[C]//Proceedings of the 11th IEEE Congress on Evolutionary Computation. Piscataway, NJ:IEEE, 2009:3285-3291. |
| [21] | 相荣荣. 协同量子粒子群优化及其应用研究[D]. 西安: 西安电子科技大学, 2012: 17-30. ( XIANG R R. Cooperative quantum-behaved particle swarm optimization and its applications[D]. Xi'an:Xidian University, 2012:17-30. ) |
| [22] | 陈世明, 方华京. 大规模智能群体的建模与稳定性分析[J]. 控制与决策, 2005, 20(5): 490-494. ( CHEN S M, FANG H J. Modeling and stability analysis of large-cale intelligent swarm[J]. Control and Decision, 2005, 20(5): 490-494. ) |




