折扣{0-1}背包问题 (Discounted {0-1}Knapsack Problem, D{0-1}KP) 是经典0-1背包问题的一个扩展形式[1-4],其思想源于商业领域的打折,在项目决策、投资和预算控制等方面具有广阔的应用背景[2]。基于动态规划求解D{0-1}KP的确定性算法是伪多项式时间的[1-2, 4],当问题规模较大并且各项的价值系数与重量系数在较大范围内取值时,耗费大量的求解时间,缺乏实用性。因此,探讨利用进化算法快速求解D{0-1}KP的可行方法是一个值得研究的问题。
目前,D{0-1}KP的研究成果还相对较少,其中Guldan[1]首先提出了D{0-1}KP问题,给出了D{0-1}KP的一个数学模型,并基于动态规划给出了一个精确算法;Rong等[2]研究了D{0-1}KP的核 (Core) 问题,并将动态规划与核相结合求解D{0-1}KP;贺毅朝等[3]给出了D{0-1}KP的两个新的数学模型,并基于精英保留策略遗传算法 (Elitist Genetic Algorithm, EGA) 提出了求解D{0-1}KP两个算法:第一遗传算法 (First Genetic Algorithm, FirEGA) 和第二遗传算法 (Second Genetic Algorithm, SecEGA);随后,又在文献[4]中给出了一系列的求解算法。
本文基于新型启发式算法——蝙蝠算法 (Bat Alogrithm, BA)[5]求解D{0-1}KP,首先提出利用双重编码的二进制蝙蝠算法 (Double codes Binary Bat Algorithm,DBBA)[6]求解D{0-1}KP;为了消除求解过程中产生的不可行解,利用文献[3]中贪心修复与优化算法 (Greedy Repair and Optimization Algorithm, GROA) 对蝙蝠个体进行修复和优化处理并计算适应度。然后,为进一步提高算法的求解精度和收敛速度提出了变异蝙蝠算法 (Mutated Double Codes Binary Bat Algorithm,MDBBA)。在DBBA基础上,加入差分演化的变异策略来提高种群的多样性,以增强算法的全局寻优能力;同时,让每只蝙蝠按照50%的概率进行Lévy飞行,以避免算法陷入局部最优。最后,对四类大规模D{0-1}KP实例的计算结果表明:对于大规模的D{0-1}KP实例,MDBBA能够快速求得一个近似比接近于1的近似解,其效果优于FirEGA[3]和DBBA。
1 D{0-1}KP定义定义[1] 给定n个均含有3个项 (或物品) 的项集,项集i(0≤i≤n-1) 中含有的3个项分别记为3i, 3i+1, 3i+2,其中前两项具有的价值系数分别为v3i和v3i+1,具有的重量系数分别为w3i和w3i+1;前两项合并到一起构成第三项3i+2,它具有的价值系数为v3i+2=v3i+v3i+1,具有的折扣重量系数为w3i+2,满足w3i+2 < w3i+w3i+1且w3i+2 > w3i,w3i+2 > w3i+1。对于每个项集i(0≤i≤n-1),项3i, 3i+1, 3i+2最多有一个被选中装入背包中。如何选择各项装入背包,使得被装入背包的所有项的重量系数之和在不超过背包载重C的前提下价值系数和最大?
Guldan给出了D{0-1}KP的第一个数学模型,描述如下:
| $ \max f(X) = \max \sum\limits_{i = 0}^{n - 1} {({x_{3i}}{v_{3i}} + {x_{3i + 1}}{v_{3i + 1}} + {x_{3i + 2}}{v_{3i + 2}})} $ | (1) |
| $ {\rm{s}}.{\rm{t}}.\;{x_{3i}} + {x_{3i + 1}} + {x_{3i + 2}} \le 1,i = 0,1, \ldots ,n - 1 $ | (2) |
| $ \sum\limits_{i = 0}^{n - 1} {({x_{3i}}{w_{3i}} + {x_{3i + 1}}{w_{3i + 1}} + {x_{3i + 2}}{w_{3i + 2}}) \le C} $ | (3) |
| $ {x_{3i}},{x_{3i + 1}},{x_{3i + 2}} \in \{ 0,1\} ,i = 0,1, \ldots ,n - 1 $ | (4) |
其中:二元变量xj(0≤i≤3n-1) 表示项j是否被装入背包中,即xj=1表示第j项被装入了背包中,xj=0表示第j项未被装入背包。显然,任意向量X =[x0, x1, x2, …, x3n-1]∈{0, 1}3n仅仅表示D{0-1}KP的一个潜在解,只有当它同时满足了约束条件 (2) 和 (3) 时才是一个可行解。
2 双重编码的蝙蝠算法蝙蝠算法 (BA) 是Yang[5]于2010年提出的一种新型启发式算法,其思想源于蝙蝠寻找猎物过程中回声定位原理。目前,该算法已引起国内外学者的广泛关注,成为计算智能研究领域的一个新的研究热点,学者们不但对算法的性能进行各种改进[7-10],并将其成功地应用到工程设计[11-13]、分类[14]、神经网络[15]和模糊聚类[16]等领域。
蝙蝠算法是解决连续变量的函数优化问题,它将种群数量为N的蝙蝠飞行的位置映射成d维问题空间中的N个解向量,通过蝙蝠种群飞行的过程来进行问题的优化求解,用求解问题的适应度函数值来衡量每个蝙蝠的位置Xi=[xi1, xi2, …, xid]的好坏,每只蝙蝠在种群最优解影响下飞行,直至达到全局最优解。为了将蝙蝠算法应用于折扣背包问题求解,这里为每只蝙蝠设置了双重编码[6, 17],即针对每只蝙蝠的实数位置Xi引入一个的二进制位置Bi=[bi1, bi2, …, bid],映射关系如式 (5)[6]:
| $ {b_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{x_{ij \ge 0}}}\\ {0,}&{{x_{ij}} < 0} \end{array}} \right. $ | (5) |
其中xij∈[-1, 1]是第i只蝙蝠在第j维的实数值。这样每只蝙蝠可表示成一个二元组 (Xi(t), Bi(t)),其中Xi(t)=[xi1(t), xi2(t), …, xid(t)] ∈[-1, 1]d是第t代第i个蝙蝠的实数位置;Bi(t)=[bi1(t), bi2(t), …, bid(t)]∈{0, 1}d是该蝙蝠的二进制位置。蝙蝠的适应度函数按它的二进制位置计算f(Bi(t)),蝙蝠的实数位置Xi(t) 按式 (6)~(8) 更新:
| $ {f_i}(t) = {f_{\min }} + ({f_{{\rm{max}}}} - {f_{\min }})*\beta $ | (6) |
| $ {\mathit{\boldsymbol{V}}_i}(t + 1) = {\mathit{\boldsymbol{V}}_i}(t) + ({\mathit{\boldsymbol{X}}_i}(t) - \mathit{\boldsymbol{Y}})*{f_i}(t) $ | (7) |
| $ {\boldsymbol{X}_i}(t + 1) = {\boldsymbol{X}_i}(t) + {\boldsymbol{V}_i}(t) $ | (8) |
其中:fi(t)∈[fmin, fmax]是第t代第i个蝙蝠的频度; β∈[0, 1]是随机数; Vi(t) 是第t代第i个蝙蝠的飞行速度; Y是第t代蝙蝠群体最优实数位置。
设 (hXi(t), hBi(t)) 为第t代第i个蝙蝠的历史最优个体;(Y, P) 为蝙蝠群最优个体。下面以求解最大约束优化问题max f(X) 为例给出具有双重编码的二进制蝙蝠算法 (DBBA)[6]的描述。
算法1 DBBA[6]。
输入 max f(X),最大迭代次数MaxIt;
输出 最优解P,适应度函数值f(P)。
步骤1 随机产生初始蝙蝠群实数位置,用式 (3) 计算得到蝙蝠的二进制位置,令迭代次数t=0。
步骤2 设置每只蝙蝠的初始速度Vi,脉冲发射速率fi、脉冲响度ai和脉冲频率ri的初始值。
步骤3 计算每只蝙蝠适应度,令其历史最好个体等于该蝙蝠个体,根据各个蝙蝠适应值找出最好的蝙蝠Xk,令全局最优等于该蝙蝠。
步骤4
While (t < MaxIt)
t + +;
For (i=1;i < d; i + +)
利用式 (3)、(4)~(6),(10) 更新蝙蝠的速度和实数位置和二进制位置,并计算适应度值
If (f(Bi(t)) > f(hBi(t))
更新该蝙蝠的历史最优个体
EndIf
If (rand1 > ri)
利用式 (9) 将蝙蝠更新到某较好蝙蝠的附近
EndIf
随机产生一个新蝙蝠 (Xnew, Bnew)
if (rand2 < ai & & > f(Bnew) > f(P))
P=Bnew, Y=Xnew;
用式 (10) 和 (11) 减小ai和增大ri
EndIf
EndFor
找到种群中历史适应度最好的蝙蝠,如果该历史最优个体好于全局最优,则替代全局最优个体 (Y, P)
EndWhile
步骤5 输出P和f(P)。
下面是算法中用到的公式。
| $ {\boldsymbol{X}_{\rm{n}}}_{{\rm{ew}}} = {\boldsymbol{X}_k}(t) + \varepsilon a;\varepsilon \in \left[ {0,1} \right]是随机数 $ | (9) |
| $ {a_i} = \partial {a_i} $ | (10) |
| $ {r_i} = {r_i}[1 - \exp ( - \gamma t)] $ | (11) |
式 (9) 中的a是所有蝙蝠响度ai的平均值;式 (10)、(11) 中0 < ∂ < 1和γ > 0都是常数因子[5],本文实验中∂=γ=0.9。关于蝙蝠算法中各公式详细介绍请参考文献[5], 限于篇幅不再赘述。
3 变异蝙蝠算法求解折扣背包问题 3.1 编码的处理根据Guldan给出的数学模型,在利用双重编码的蝙蝠算法求解D{0-1}KP时,个体蝙蝠的十进制编码X=[x0, x1, x2, …, x3n-1]∈[0, 1]3n,对应的二进制编码为B=[b0, b1, b2, …, b3n-1] ∈{0, 1}3n,当bj=1(0≤j≤3n-1) 时,表示项j被装入背包,bj=0表示项j没有被装入。这种编码方法虽然简单易行,但也存在一个明显的缺点,就是不可行解会非常多[3]。本文将GROA[3]应用到对蝙蝠个体适应度值的计算中,消除不可行解并对可行解进行优化。设V={{v3i, v3i+1, v3i+2}|0≤i≤n-1}为D{0-1}KP的各项的价值集,W={{w3i, w3i+1, w3i+2}|0≤i≤n-1}为各项的重量集,C为背包载重。将3n个项根据价值密度vj/wj(0≤j≤3n-1) 由大到小排序,并按照排序后的顺序将各项的下标存入数组sort[0…3n-1]中。设置数组flag[0…n-1]∈{0, 1}n标识各项集的状态,flag[i]=0表示项集i中没有项被装入背包,flag[i]=1表示项集i中恰有一项被装入背包,
算法2 GETFIT。
输入 原蝙蝠个体 (X, B) 和sort[0…3n-1];
输出 修正后的蝙蝠个体 (G, E) 及适应度值f(E)。
weight=0, value=0
For (j=0; j < 3n-1; j+ +)
ej=0
For (i=0; i < n-1; i+ +)
flag[i]=0
For (j=0; j < 3n-1; j+ +)
If (bsort[j]=1 & weight+wsort[j]≤C & flag[
esort[j]=1,gsort[j]=xsort[j],value=value+vsort[j]
weight=weight+wsort[j],flag[
EndIf
EndFor
For (j=0; j < 3n-1; j+ +)
If ((weight+wsort[j]≤C) & flag[
esort[j]=1,gsort[j]=rand(), rand()∈[0, 1]
weight=weight+wsort[j],flag[
value=value+vsort[j]
EndIf
EndFor
f(E)=value
return (G, E, f(E))
将GETFIT算法应用于算法DBBA求解适应度值,即可求解D{0-1}KP,第4章对比实验中算法DBBA就是使用GETFIT后的DBBA。
3.2 基于差分的变异策略差分演化的变异算子存在多种形式, 其一般表示为DE/x/y/z[18],x表示变异算子中差异向量进行重组的基准个体是随机选取的还是当前群体的最优个体;y表示参与重组的差异向量个数;z表示重组所采用的方式,主要有指数重组方式和二项式重组方式,这里使用二项式重组。文献[19]把二项式重组变异算子分为3类:第1类为DE/rand/1/bin和DE/rand/2/bin;第2类为DE/best/1/bin和DE/best/2/bin;第3类是DE/rand-to-best/1/bin模式。为了提高蝙蝠算法种群的多样性,本文从每类模式中选择一种分别应用于蝙蝠算法中,测试其有效性。测试数据将在第4章给出。变异策略用算法DEM (Different Evolution Mutation) 实现:
算法3 DEM。
输入 原蝙蝠个体,原适应度值;
输出 经过变异策略后的蝙蝠个体,新适应度值。
1) 应用差分变异算子产生子蝙蝠个体十进制位置;
2) 根据式 (3) 计算子蝙蝠的二进制位置;
3) 用GETFIT得到子蝙蝠的适应值;
4) 如果子蝙蝠的适应度好于原蝙蝠;
5) 用子蝙蝠替换原蝙蝠。
变异操作使得蝙蝠个体之间可以相互交流,增加了蝙蝠群体探索和寻优能力,另外精英个体保留机制提高了算法的收敛速度。
3.3 Lévy飞行启发式算法在寻优过程中往往容易陷入局部极值,这里通过蝙蝠个体的Lévy飞行来降低算法陷入局部极值的可能性。Lévy飞行是一种随机游走过程,它的步长是一种连续的重尾分布[20]。从数学角度看,Lévy飞行行为体现出的是一类非高斯随机过程,其平稳增量服从Lévy稳定分布,Lévy飞行过程中会发生大的跳跃且方向多变,其典型轨迹表现为由较小跳跃组成的聚集被较大的跳跃分隔开的现象,可以借助大的跳跃逃离局部极值[21]。为了避免算法过早地陷入局部极值中,在算法中,每次迭代后个体蝙蝠按照一定概率 (本文定为0.5) 进行Lévy飞行,按式 (12) 产生飞行后的十进制位置[20]:
| $ {X'_i} = {X_i} + a \oplus {\rm{L\acute{e}vy}}\left( \lambda \right) $ | (12) |
其中:Xi为原蝙蝠实数位置,Xi′为飞行后的实数位置, 其中Lévy (λ) 来自于Lévy分布[20]。用式 (5) 确定其二进制位置后通过GETFIT算法计算飞行后的适应度值,如果适应度优于原蝙蝠则用新位置替代原蝙蝠的位置。
3.4 变异蝙蝠算法求解折扣背包问题流程用算法MDBBA求解D{0-1}问题的蝙蝠算法流程如图 1所示。每只蝙蝠的适应度均由算法GETFIT求得;用式 (6)~(8)、(5) 更新蝙蝠的速度Vi(t) 和实数位置Xi(t) 和二进制位置Bi(t)。MP是蝙蝠进行变异操作的概率,本文设为0.8;rand1,rand2,rand3,rand4均为在[0, 1]上产生的随机数。

|
图 1 变异蝙蝠算法求解折扣背包算法流程 Figure 1 Flowchart of mutated bat algorithm for solving D{0-1}KP |
使用文献[3]给出的4类D{0-1}KP实例:不相关D{0-1}KP实例 (Uncorrelated instances of D{0-1}KP,UDKP)、弱相关D{0-1}KP实例 (Weakly correlated instances of D{0-1}KP,WDKP)、强相关D{0-1}KP实例 (Strongly correlated instances of D{0-1}KP, SDKP) 和逆向强相关D{0-1}KP实例 (Inverse strongly correlated instances of D{0-1}KP,IDKP),其中每类有10个不同规模的实例。关于实例详细介绍请参考文献[3]。本文针对4类D{0-1}KP实例进行了两组实验:实验1是将三种差分的变异算子分别与蝙蝠算法结合,通过对实例运行结果的箱图 (BOXPLOT) 分析确定使用的变异算子; 实验2是通过四类大规模D{0-1}KP实例的各种计算结果, 对MDBBA与DBBA和文献[3]的FirEGA算法进行比较。仿真计算所使用微机的硬件环境为,操作系统Windows 10,编程环境VC+ +2010。MDBBA与DBBA各个参数的设置:Xmax=1.0;Xmin=-1.0;Vmax=1.0;fmin=0.01;fmax =0.071;蝙蝠个体初始脉冲频率r0=0.05;初始化脉冲响度a0=1.0;脉冲音强衰减系数和脉冲频率增强系数=0.9;变异概率MP=0.8,Lévy飞行概率为0.5;种群规模是40;迭代次数均等于实例的规模 (即3n)。FirEGA算法数据来自文献[3]。
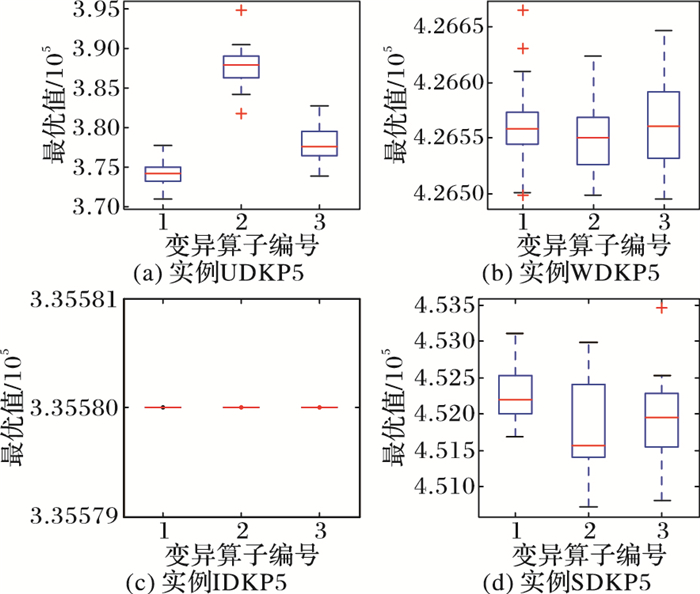
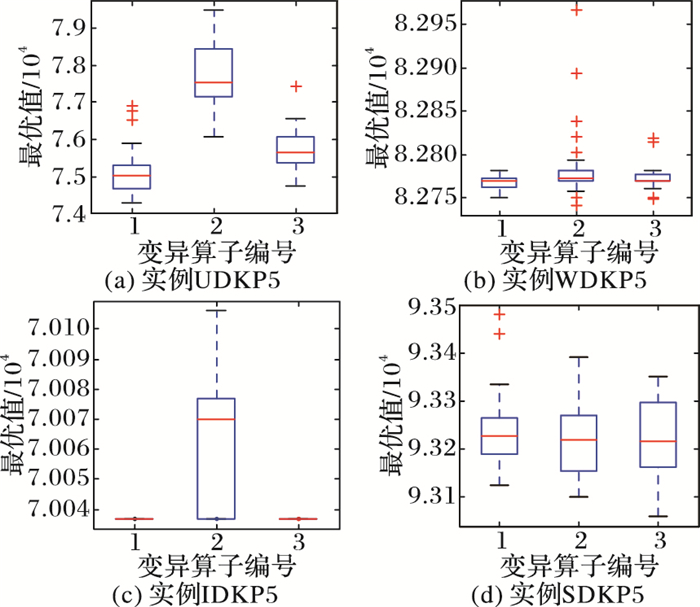
4.1 变异算子性能比较这里将DE/rand/1/bin、DE/best/1/bin、DE/rand-to-best/1/bin (编号为1、2、3) 三种变异算子分别应用于蝙蝠算法中,测试其有效性。抽取维数为100和500的8组实例进行测试。图 2、3是30次独立运行各组合形式得到的最优值的统计结果形成的箱图。根据八个箱图比较, 第2类模式的变异算子 (编号2) 使得算法有较高的稳定性,产生的最优值也基本都高于另外两类模式,所以本文确定使用DE/best/1/bin作为变异算子。实验2中算法MDBBA变异部分使用该变异算子。
|
图 2 三种不同算子在100维四类实例下的比较 Figure 2 Comparison of 3 different operators in 4 types of 100 dimensions |
|
图 3 三种不同算子在500维四类实例下的比较 Figure 3 Comparison of 3 different operators in 4 types of 500 dimensions |
利用FirEGA、DBBA与MDBBA求解四类D{0-1}KP实例的计算结果见表 1~4,其中Opt为由动态规划法 (记为DPDKP) 计算出的实例最优值;Best、Worst和Mean分别为FirEGA,DBBA与MDBBA在30次独立计算中得到的所有结果的最好值、最差值以及所有结果的数学期望;Opt/Best、Opt/Worst和Opt/Mean分别表示以上各值的近似比[22-23]。
| 表 1 对实例UDKP1~UDKP10的实验结果比较 Table 1 Comparison of experimental results of examples UDKP1 ~ UDKP10 |
| 表 2 对实例WDKP1~WDKP10的实验结果对比 Table 2 Comparison of Experimental Results of Examples WDKP1 ~ WDKP10 |
| 表 3 对实例IDKP1~IDKP10的实验结果对比 Table 3 Comparison of Experimental Results of Examples IDKP1 ~ IDKP10 |
| 表 4 对实例SDKP1~SDKP10的实验结果对比 Table 4 Comparison of experimental results of examples SDKP1 ~ SDKP10 |
为更直观地比较实验结果,将FirEGA、DBBA与MDBBA求解四类D{0-1}KP实例的最好值近似比和平均值近似比以曲线图的形式展现出来,如图 4~11。
|
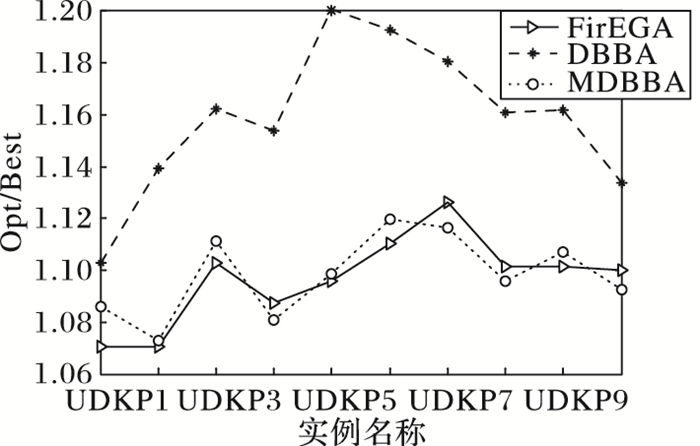
图 4 UDKP类实例最好值的近似比 Figure 4 Approximate ratio of the best value of UDKP |
|
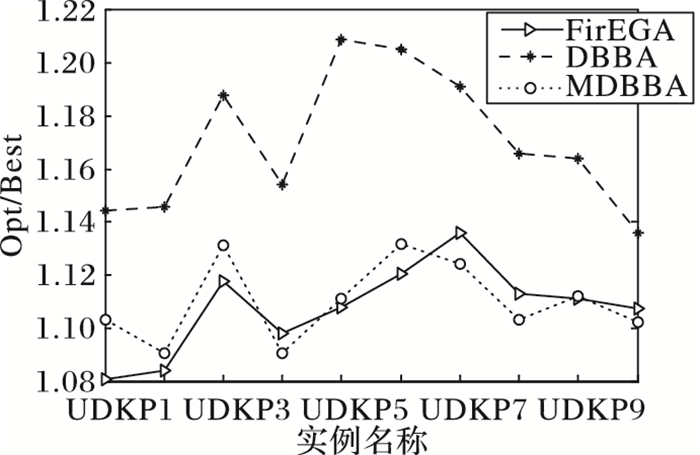
图 5 UDKP类实例平均值的近似比 Figure 5 Approximate ratio of the average of UDKP |
|
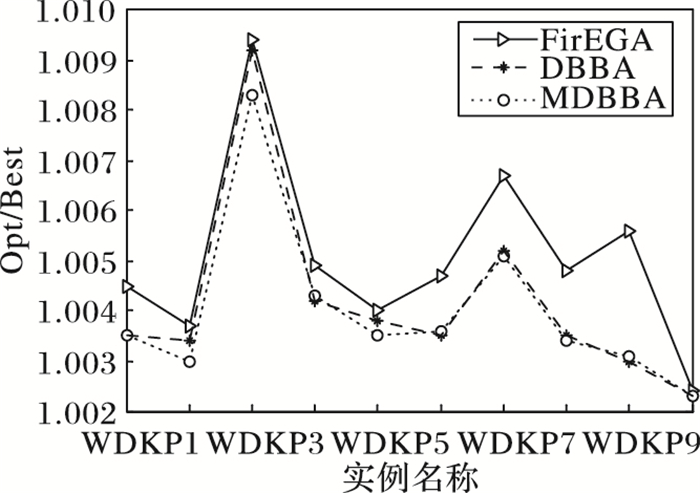
图 6 WDKP类实例最好值的近似比 Figure 6 Approximate ratio of the best value of WDKP |
|
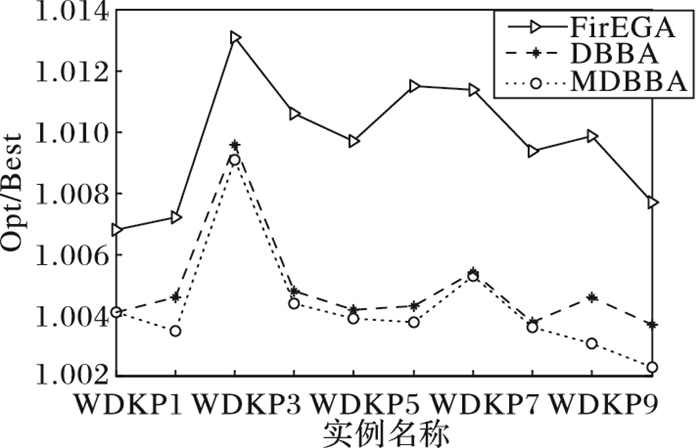
图 7 WDKP类实例平均值的近似比 Figure 7 Approximate ratio of the average of WDKP |
|
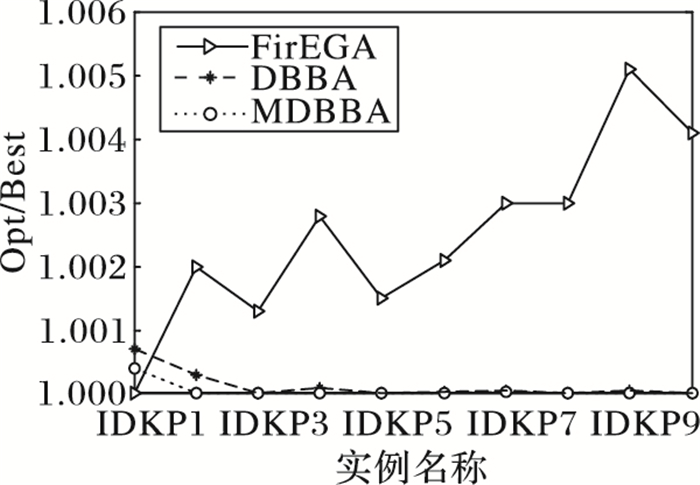
图 8 IDKP类实例最好值的近似比 Figure 8 Approximate ratio of the best value of IDKP |
|
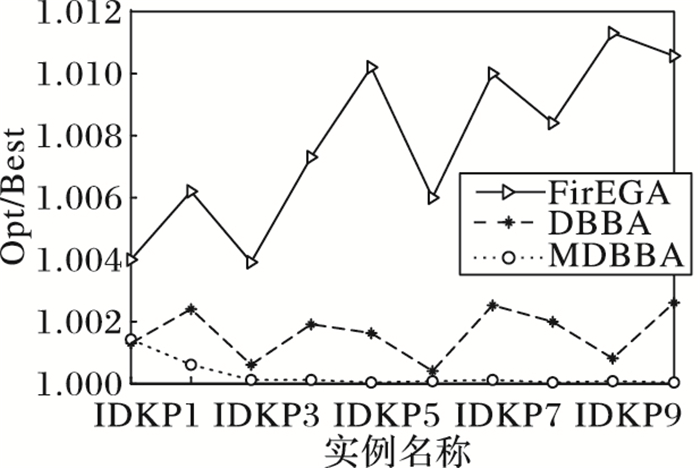
图 9 IDKP类实例平均值的近似比 Figure 9 Approximate ratio of the average of IDKP |
|
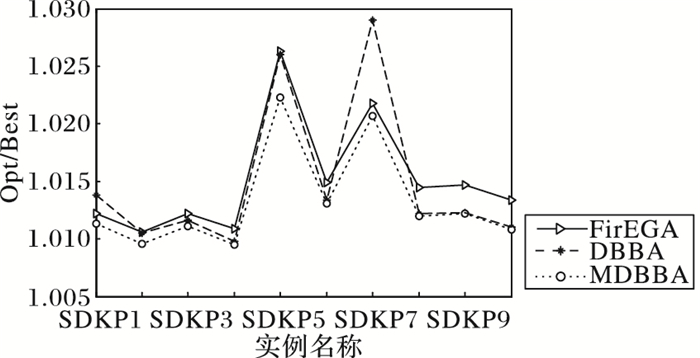
图 10 SDKP类实例最好值的近似比 Figure 10 Approximate ratio of the best value of SDKP |
|
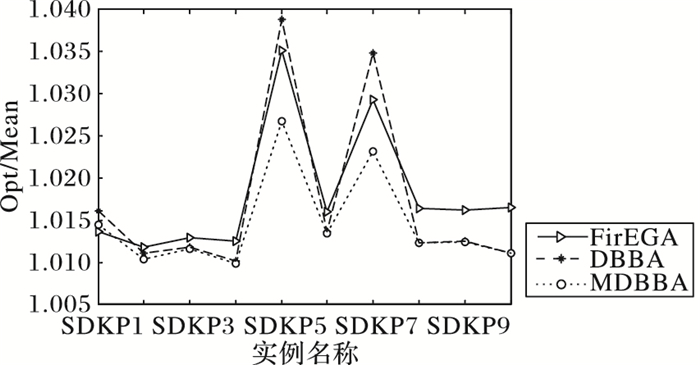
图 11 SDKP类实例平均值的近似比 Figure 11 Approximate ratio of the average of SDKP |
从表 1中可以看出:FirEGA求解UDKP实例所得最好值的近似比基本在1.10左右,平均值和最差值的近似比均不超过1.144 1;DBBA所得最好值的近似比在1.16左右,平均值和最差值的近似比都在1.213 6以下;MDBBA求解UDKP实例所得最好值的近似比在1.09左右,平均值和最差值的近似比均不超过1.148 3。图 4是三种算法求解UDKP1~UDKP10实例的最好值的近似比比较,图 5是三种算法求解UDKP1~UDKP10实例平均值的近似比比较图。从两图中可以看出,DBBA求解能力最差,经过加入变异和Lévy飞行后的MDBBA求解能力有很大的提高,最好值近似比和平均值近似比基本和FirEGA相当,有4个实例超出FirEGA。
从表 2中可以看出FirEGA求解WDKP实例所得到的最好值的近似比不超过1.009 4,平均值的近似比不超过1.013 1,最差值的近似比不超过1.028 2;DBBA求解WDKP实例所得到的最好值的近似比不超过1.009 2,平均值的近似比不超过1.009 6,最差值的近似比不超过1.034 0;MDBBA求解WDKP实例所得到的最好值的近似比不超过1.008 3,平均值的近似比不超过1.009 1,最差值的近似比不超过1.009 2。图 6是三种算法求解WDKP1~WDKP10实例的最好值的近似比比较,图 7是平均值的近似比比较。DBBA在求解WDKP实例中求得最优值近似比,平均值近似比都好于FirEGA;而MDBBA的最好值近似比、平均值近似比在每个实例上都优与DBBA。
从表 3中可以看出:FirEGA求解IDKP实例所得最好值的近似比不超过1.005 1,平均值的近似比不超过1.011 3,最差值的近似比不超过1.053 4;DBBA求解IDKP实例所得到的最好值的近似比不超过1.000 7,平均值的近似比不超过1.002 5,最差值的近似比不超过1.026 4;MDBBA求解IDKP实例所得到的最好值的近似比不超过1.000 4,平均值的近似比不超过1.001 4,最差值的近似比不超过1.003 7。图 8是三种算法求解IDKP1~IDKP10实例的最好值的近似比,图 9是平均值的近似比。从两图中明显看出DBBA和MDBBA求解效果明显优于FirEGA;DBBA和MDBBA比较,MDBBA求解效果和平均求解能力都更好。
从表 4中可以看出:FirEGA求解SDKP实例所得到的最好值的近似比均不超过1.026 3,平均值的近似比不超过1.035 1,最差值的近似比也均不超过1.042 3;DBBA求解SDKP实例所得到的最好值的近似比不超过1.026 0,平均值的近似比不超过1.038 8,最差值的近似比不超过1.048 0;MDBBA求解SDKP实例所得到的最好值的近似比不超过1.022 3,平均值的近似比不超过1.026 7,最差值的近似比不超过1.033 3。图 10是三种算法求解SDKP1~SDKP10实例的最好值的近似比比较,图 11是平均值的近似比比较图,从两图中看出:双重编码蝙蝠算法DBBA求解SDKP实例能力比FirEGA略弱,MDBBA在求解能力上优于FirEGA。
为了进一步比较双重编码蝙蝠算法DBBA和变异双重编码蝙蝠算法MDBBA的平均求解性能,图 12给出它们30次独立运行实例UDKP5、WDKP5、SDKP5和IDKP5的平均收敛曲线。由图可以看出:MDBBA的平均收敛速度非常快,基本上在不超过0.2*MaxIt的迭代次数内即可获得极好的结果;DBBA的平均收敛速度相对慢,并且它的平均求解结果也明显比MDBBA的差。
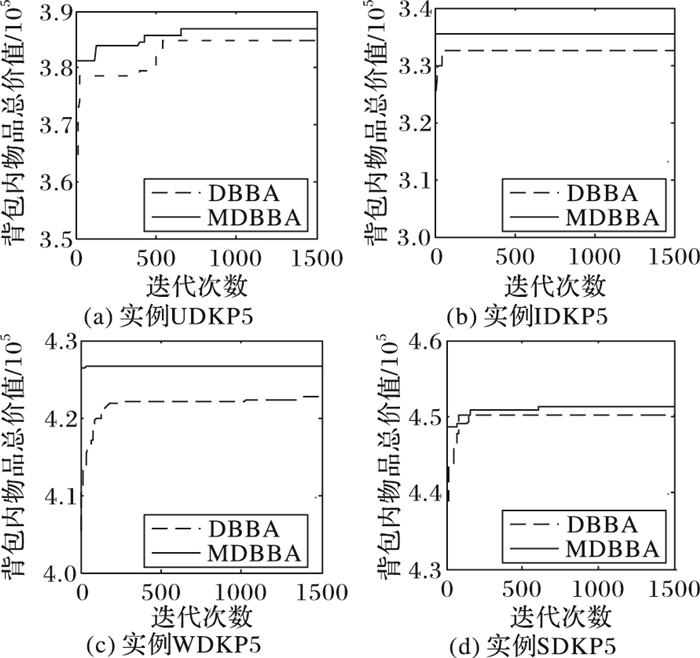
|
图 12 对DBBA和MDBBA平均收敛曲线比较 Figure 12 Comparison of average convergence curve of DBBA and MDBBA |
基于对四类D{0-1}KP实例的计算、比较和分析可以知,对于项的价值系数和重量系数均在大范围内随机取值的D{0-1}KP实例,MDBBA均能够求得一个近似比接近于1的近似解,是求解大规模难D{0-1}KP实例的有效且实用的进化算法。从算法求得的最好结果来看,DBBA、MDBBA和FirEGA的求解能力基本相当,DBBA在求解UDKP实例中效果明显不如MDBBA和FirEGA;从算法的平均求解性能来看,MDBBA的求解效果优于FirEGA和DBBA。
5 结语本文研究了如何利用变异蝙蝠算法求解D{0-1}KP,提出利用双重编码方式求解D{0-1}KP,将贪心和优化策略应用于个体适应度求解中;针对蝙蝠算法易早熟、求解精度不高的缺陷,在蝙蝠群更新位置后利用差分变异增加种群多样性,提高全局搜索能力;通过蝙蝠个体的Lévy飞行避免群体过早的陷入局部极值。对四类大规模D{0-1}KP实例的计算结果比较与分析,MDBBA不受实例中各项的价值系数、重量系数和背包载重的大小影响,对于大规模的难D{0-1}KP实例,能够快速求得一个近似比接近于1的近似解。比基本双重编码的蝙蝠算法无论在收敛速度还是在寻优能力上都有极大提高,是求解大规模难D{0-1}KP实例的实用进化算法。
| [1] | GULDAN B. Heuristic and exact algorithms for discounted knapsack problems[D]. Nuremberg:University of Erlangen-Nuremberg, 2007. |
| [2] | RONG A, FIGUEIRA J R, KLAMROTH K. Dynamic programming based algorithms for the discounted {0-1} knapsack problem[J]. Applied Mathematics and Computation, 2012, 218(12): 6921-6933. doi: 10.1016/j.amc.2011.12.068 |
| [3] | 贺毅朝, 王熙照, 李文斌, 等. 基于遗传算法求解折扣{0-1}背包问题的研究[J]. 计算机学报, 2016, 39(12): 2614-2630. ( HE Y C, WANG X Z, LI W B, et al. Research on genetic algorithms for the discounted {0-1} knapsack problem[J]. Chinese Journal of Computers, 2016, 39(12): 2614-2630. doi: 10.11897/SP.J.1016.2016.02614 ) |
| [4] | HE Y, WANG X, HE Y, et al. Exact and approximate algorithms for discounted {0-1} knapsack problem[J]. Information Sciences, 2016, 369(10): 634-647. |
| [5] | YANG X. A new metaheuristic bat-inspired algorithm[C]//NICSO 2010:Nature Inspired Cooperative Strategies for Optimization. Berlin:Springer, 2010, 284:65-74. |
| [6] | 吴聪聪, 贺毅朝, 陈嶷瑛, 等. 求解0-1背包问题的二进制蝙蝠算法[J]. 计算机工程与应用, 2015, 51(19): 71-74. ( WU C C, HE Y C, CHEN Y Y, et al. Binary bat algorithm for solving 0-1 knapsack problem[J]. Computer Engineering and Applications, 2015, 51(19): 71-74. doi: 10.3778/j.issn.1002-8331.1501-0096 ) |
| [7] | 贺兴时, 丁文静, 杨新社. 基于模拟退火高斯扰动的蝙蝠优化算法[J]. 计算机应用研究, 2013, 31(2): 392-397. ( HE X S, DING W J, YANG X S. Bat algorithm based on simulated annealing and Gaussian perturbations[J]. Application Research of Computers, 2013, 31(2): 392-397. ) |
| [8] | 谢健, 周永权, 陈欢. 一种基于Lévy飞行轨迹的蝙蝠算法[J]. 模拟识别与人工智能, 2013, 26(9): 829-837. ( XIE J, ZHOU Y Q, CHEN H. A bat algorithm based on Lévy flights trajectory[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(9): 829-837. ) |
| [9] | 刘长平, 叶春明. 具有混沌搜索策略的蝙蝠优化算法及性能仿真[J]. 系统仿真学报, 2013, 25(6): 1183-1188. ( LIU C P, YE C M. Bat algorithm with chaotic search strategy and analysis of its property[J]. Journal of System Simulation, 2013, 25(6): 1183-1188. ) |
| [10] | YANG X. Bat algorithm for multiobjective optimization[J]. International Journal of Bio-Inspired Computation, 2011, 3(5): 267-274. doi: 10.1504/IJBIC.2011.042259 |
| [11] | YANG X, GANDOMI A H. Bat algorithm:a novel approach for global engineering optimization[J]. Engineering Computations, 2012, 29(5): 464-483. doi: 10.1108/02644401211235834 |
| [12] | LEMMA T A, BIN M H F. Use of fuzzy systems and bat algorithm for energy modeling in a gas turbine generator[C]//Proceedings of the 2011 IEEE Colloquium on Humanities, Science and Engineering. Piscataway, NJ:IEEE, 2011:305-310. |
| [13] | 盛晓华, 叶春明. 基于蝙蝠算法的PFSP调度干扰管理研究[J]. 计算机工程与应用, 2014, 50(8): 241-246. ( SHENG X H, YE C M. Research of bat algorithm for disruption management on PFSP scheduling[J]. Computer Engineering and Applications, 2014, 50(8): 241-246. ) |
| [14] | MISHRA S, SHAW K, MISHRA D. A new meta-heuristic bat inspired classification approach for microarray data[J]. Procedia Technology, 2012, 4(1): 802-806. |
| [15] | KHAN K, SAHAI A. A comparison of BA, GA, PSO, BP and LM for training feed forward neural networks in e-learning context[J]. International Journal of Intelligent Systems and Applications, 2012, 4(7): 23-29. doi: 10.5815/ijisa |
| [16] | KHAN K, NIKOV A, SAHAI A. A fuzzy bat clustering method forergonomic screening of office workplaces[C]//Proceedings of the 3rd International Conference on Software, Services and Semantic Technologies. Berlin:Springer, 2011:59-66. |
| [17] | 贺毅朝, 王彦祺, 刘建芹. 一种适于求解离散问题的二进制粒子群优化算法[J]. 计算机应用与软件, 2007, 24(1): 157-159. ( HE Y C, WANG Y Q, LIU J Q. A new binary particle swarm optimization for solving discrete problems[J]. Computer Applications and Software, 2007, 24(1): 157-159. ) |
| [18] | NOMAN N, IBA H. Enhancing differential evolution performance with local search for high dimensional function optimization[C]//Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York:ACM, 2005:967-974. |
| [19] | 贺毅朝, 王熙照, 刘坤起, 等. 差分演化的收敛性分析与算法改进[J]. 软件学报, 2010, 21(5): 875-885. ( HE Y C, WANG X Z, LIU K Q, et al. Convergent analysis and algorithmic improvement of differential evolution[J]. Journal of Software, 2010, 21(5): 875-885. ) |
| [20] | YANG X, DEB S. Cuckoo search via Lévy flights[C]//Proceedings of World Congress on Nature & Biologically Inspired Computing. Piscataway, NJ:IEEE, 2009:210-214. |
| [21] | 刘长平, 叶春明. 具有Lévy飞行特征的蝙蝠算法[J]. 智能系统学报, 2013, 8(3): 240-246. ( LIU C P, YE C M. Bat algorithm with the characteristics of Lévy flights[J]. CAAI Transactions on Intelligent Systems, 2013, 8(3): 240-246. ) |
| [22] | CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to Algorithms[M]. Cambridge: MIT Press, 2001 : 1117 -1119. |
| [23] | ALSUWAIYEL M H. Algorithms Design Techniques and Analysis[M]. Singapore: World Scientific Publishing Company, 1999 : 410 -418. |




