2. 武警部队 密码与信息安全保密重点实验室 (武警工程大学), 西安 710086
2. Key Laboratory of Chinese Armed Police Force for Cryptology and Information Security (Engineering College of Chinese Armed Police Force), Xi'an Shaanxi 710086, China
安全多方计算 (Secure Multi-party Computation, SMC)[1]主要研究在网络环境中互不信任的多用户之间的协作计算问题。它可以概括成以下数学模型:在一个分布式网络中, 有n个互不信任的参与者P1, P2, …, Pn, 每个参与者Pi(本文i取值均为i=1, 2, …, n) 秘密输入xi, 他们共同执行函数F:(x1, x2, …, xn)→y, 在计算过程中, 任意参与者Pi不能得到其他参与者Pj(j≠i) 的任何输入信息。
安全多方计算是由姚期智教授提出的百万富翁问题 (Millionaires' problem)[1]延伸而来。安全多方计算的参与者利用各自私密数据协同完成某种计算, 但是并不泄露各自私密数据, 因而使人们在最大限度利用私密数据的同时又不破坏数据的隐私性。目前, 安全多方计算的相关应用十分广泛[2-6]。Goldwasser[7]曾说:“安全多方计算是密码学领域里一个极其重要的工具, 丰富的理论将使它成为计算科学必不可少的组成部分。”
在传统的安全多方计算加密方案中, 计算的参与方都能得到最终结果, 比如保密电子拍卖[6], 所有竞拍者均能获知最高出价是多少。然而, 这种粗粒度的访问控制可能不适用于一些应用, 现实中往往要求某些特定用户才可得到最终结果。考虑这样一个场景:一家大公司, n个员工将私密消息以密文形式存储在公司云服务器上, 现在调用某种安全多方算法对密文进行计算, 计算结果要求只能由公司董事会成员联合解密。针对此场景, 现行解决方案一般是由公司董事会成员生成联合密钥 (PK, SK), 员工使用公钥PK加密明文, 云服务器再将多方计算结果反馈给董事会, 董事会成员利用私钥SK解密。但是, 董事会成员只要有一人将私钥SK泄露出去, 非法用户就能破解密文。因此, 现行方案是不安全的。
谓词加密 (Predicate Encryption, PE) 由Katz等[8]提出。谓词加密是一种新的加密方式, 可以提供更加精细、灵活的功能, 如对加密数据的细粒度访问控制、带细粒度关键字搜索的公钥加密等。在谓词加密系统中, 密钥与谓词相关联, 密文则与属性向量相关联。具体而言, 私钥skf对应谓词f, 密文加密时被赋予属性向量I, 当且仅当用户谓词满足f(I)=1时, 密文才能被正常解密, 由此达到了对密文的访问控制的目的。基于谓词加密可以构建很多细粒度加密方案, 比如IBE (Identity-Based Encryption)[9-10]、ABE (Attribute-Based Encryption)[11-12]、HVE (Hidden-Vector Encryption)[13]。
为了解决安全多方计算最终结果的访问控制问题, 借鉴谓词加密的思想, 本文在文献[14-15]的谓词加密方案的基础上, 构建了一个不可区分的属性隐藏抵抗选择明文攻击 (INDistinguishable Attribute-Hiding against Chosen Plaintext Attacks, IND-AH-CPA) 安全的支持安全多方同态乘积计算的谓词加密方案, 可以实现对安全多方计算结果的指定用户联合解密, 该方案具有乘法同态性。
1 预备知识 1.1 双线性映射G、GT是由大素数p生成的循环群, g为生成元, 群阶为p, 若群G、GT中的离散对数问题均为困难问题, 则双线性映射e:G×G→GT满足下列性质:
1) 双线性性:对任意u, v∈G和a, b∈ Zp, 都有e(ua, vb)=e(u, v)ab。
2) 非退化性:存在u, v∈G, 使得e(u, v)≠1。
3) 可计算性:存在有效算法使得对任意u, v∈G, 都可以计算出e(u, v)。
1.2 支持安全多方计算的谓词加密支持安全多方计算的谓词加密方案支持以下函数:
| $ F:Ke{y_{{f_\mathit{\boldsymbol{\nu }}}}} \times {\rm{C}}{{\rm{T}}_\mathit{\boldsymbol{\chi }}} \to \left\{ {0,1} \right\}* $ |
其中:Keyfν是与谓词相关联的密钥, CTχ是与属性相关联的密文, χ,
支持安全多方计算的谓词加密方案包括下列五个子算法:
1) 初始化算法。输入相关安全参数1λ, 输出公钥PK和主密钥MK。
2) 密钥产生算法。输入主密钥MK和用户的谓词向量ν, 输出解密密钥skν。
3) 加密算法。输入公钥PK、属性向量χ和对应明文m, 输出密文c。
4) 安全多方计算。输入多个用户产生的密文集合{ci}, 输出最终加密结果C= f(c1, c2, …, cn)。
5) 解密算法。输入解密密钥skν密文C, 当且仅当fν (χ)=1时, 输出M= f(m1, m2, …, mn)。
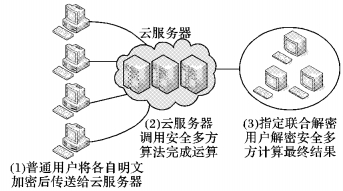
1.3 应用场景及系统模型图 1为安全多方谓词加密应用场景及系统模型。
|
图 1 安全多方谓词加密应用场景及系统模型 Figure 1 SMC-PE model and application scenario |
方案的构造中使用三种实体:
1) 普通用户。存储和计算能力都相对较弱, 在参与安全多方计算时, 得不到其他任意用户的任何输入信息。
2) 云服务器。有大量的存储空间和强大的计算能力, 能为用户提供云存储服务及云计算服务, 但是云服务器上的数据可能会遭受黑客的恶意攻击, 所以必须对数据加密以确保安全性。
3) 指定联合解密用户。拥有最终结果的解密权, 云服务器将安全多方计算得到的最终结果反馈给事先指定用户, 由他们完成联合解密。
1.3.2 方案步骤第1步 普通用户将各自明文加密后的密文集合{ci}传送给云服务器;
第2步 云服务器调用安全多方谓词加密算法完成同态乘积计算;
第3步 云服务器将计算结果反馈给事先指定的联合解密用户, 由他们解密安全多方计算最终结果。
1.4 安全模型本文的安全模型借鉴自文献[8]。
初始化 挑战者运行初始化算法得到相关参数, 把公钥传给敌手。
阶段1 敌手被允许查询多组谓词向量ν所对应的解密密钥skν。
挑战 敌手向挑战者发送两个长度相等的明文消息m0和m1, 以及它们对应的属性向量χ0和χ1, 并且针对阶段1所有查询的谓词向量ν, 满足fν(χ0)≠1, fν(χ1)≠1。挑战者以抛掷硬币的方式随机选择mb, 并用属性χb和公钥加密明文mb, 将得到挑战密文
阶段2 敌手可以继续按照阶段1的方式进行查询且满足fν(χ0)≠1, fν(χ1)≠1。
猜测 敌手输出关于b的猜测b′。
所以, 敌手的IND-AH-CPA[16]安全优势定义为
定义1 支持安全多方计算的谓词加密方案是IND-AH-CPA安全的, 当敌手在上述安全游戏中多项式时间内优势可以忽略不计。
文献[8]指出, 谓词方案达到attribute-hiding安全是指加密密文既隐藏明文信息又不泄露属性信息, 与之相对的payload-hiding安全则不保护属性信息。在一些应用场合, 必须要求属性信息也不能被泄密, 所以payload-hiding安全是不能被接受的。
1.5 安全假设本文设计的谓词加密方案, 其安全性建立在Boneh等[17]提出的基于双线性映射子群判定问题的扩展问题之上。
以下假设和定义来自文献[14]。
定义大素数p1、p2、p3, 群G和GT为阶N= p1p2p3的循环群, 群Gp1、Gp2、Gp3是群G的子群, 其阶分别为p1、p2、p3, 双线性映射e:G×G→GT。
假设1 给定群生成算法ψ, 定义如下分布:
| $ \begin{array}{l} Q = (N = {p_1}{p_2}{p_3},G,{G_{\rm{T}}},e) \leftarrow \psi \\ \;\;\;\;\;\;\;g,h \leftarrow {G_{{p_1}}},{X_3} \leftarrow {G_{{p_3}}},\\ \;\;\;\;\;\;\;D = (Q,g,h,{X_3}),\\ \;\;\;\;\;\;\;{T_0} \leftarrow {G_{{p_1}}},{T_1} \leftarrow {G_{{p_1}}}_{{p_2}} \end{array} $ |
定义算法A能够区分某一元素属于Gp1或者Gp1p2的优势为:
| $ Adv{1_{\psi ,A}}(\lambda ) = \left| {\Pr \left[ {A(D,{T_0}) = 0} \right] - \Pr \left[ {A(D,{T_1}) = 0} \right]} \right| $ |
定义2 如果对任意多项式时间算法A, 优势Adv1ψ, А(λ) 都是可以忽略不计的, 那么群生成算法ψ就满足假设1。
假设2 给定群生成算法ψ, 定义如下分布:
| $ \begin{array}{l} Q = {\rm{(}}N = {p_1}{p_2}{p_3},G,{G_{\rm{T}}},e{\rm{)}} \leftarrow \psi \\ \;\;\;\;\;\;\;g,h,{X_1} \leftarrow {G_{{p_1}}},{X_2},{Y_2} \leftarrow {G_{{p_2}}},{X_3},{Y_3} \leftarrow {G_{{p_3}}},\\ \;\;\;\;\;\;\;D = {\rm{(}}Q,g,h,{X_3},{X_1}{X_2},{Y_2}{Y_3}{\rm{)}},\\ \;\;\;\;\;\;\;{T_0} \leftarrow {G_{{p_1}}}_{{p_3}},{T_1} \leftarrow G \end{array} $ |
定义算法A能够区分某一元素属于Gp1p3或者G的优势为:
| $ Adv{2_{\psi ,A}}(\lambda ) = \left| {\Pr \left[ {A(D,{T_0}) = 0} \right] - \Pr \left[ {A(D,{T_1}) = 0} \right]} \right| $ |
定义3 如果对任意多项式时间算法A, 优势Adv2ψ, А(λ) 都是可以忽略不计的, 那么群生成算法ψ就满足假设2。
假设3 给定群生成算法ψ, 定义如下分布:
| $ \begin{array}{l} Q = {\rm{(}}N = {p_1}{p_2}{p_3},G,{G_{\rm{T}}},e{\rm{)}} \leftarrow \psi ,r \in {{\bf{Z}}_N},\\ \;\;\;\;\;\;\;g,h \leftarrow {G_{{p_1}}},{X_2},{Y_2},{Z_2} \leftarrow {G_{{p_2}}},{X_3} \leftarrow {G_{{p_3}}},\\ \;\;\;\;\;\;\;D = {\rm{(}}Q,g,{X_3},{Z_2},{g^r}{X_2},h{Y_2}{\rm{)}},\\ \;\;\;\;\;\;\;{T_0} = e{\left( {g,h} \right)^r},{T_1} \leftarrow G \end{array} $ |
定义算法A能够区分某一元素是T0或者属于GT的优势为:
| $ Adv{3_{\psi ,A}}(\lambda ) = \left| {\Pr \left[ {A(D,{T_0}) = 0} \right] - \Pr \left[ {A(D,{T_1}) = 0} \right]} \right| $ |
定义4 如果对任意多项式时间算法A, 优势Adv3ψ, А(λ) 都是可以忽略不计的, 那么群生成算法ψ就满足假设3。
2 支持安全多方同态乘积计算的谓词加密方案本文基于文献[14-15]提出的谓词加密方案, 构建了一个IND-AH-CPA安全的支持安全多方同态乘积计算的谓词加密方案, 能够实现对安全多方计算最终结果的指定用户联合解密, 该方案具有乘法同态性。谓词类为
Setup (1λ):运行初始化算法生成Q=(N= p1p2p3, G, GT, e), G, GT为N阶循环群, 随机选择g, h∈Gp1, 定义Z=e(g, g), 公钥是
| $ PK{\rm{ = }}\left\{ {g,h,{g_1} = {g^a},{{\left\{ {{{\rm{T}}_i} = {g^{{t_i}}}} \right\}}_{i{\rm{ = }}1,2, \cdots ,n}}} \right\} $ |
主密钥MK={a, {ti}}, 其中
KeyGen (MK, ν):用户的谓词向量为ν ={v1, v2, …, vn}, 选择随机数s∈ ZN, 生成解密密钥:
| $ s{k_{\bf{v}}} = \left\{ {\left\{ {{d_i} = {{(h{g^{s{v_i}}})}^{\frac{1}{{a - {t_i}}}}}} \right\}} \right\} $ |
Enc (PK, mi):为方便展示算法细节, 本文指定最终结果只能由Alice (拥有谓词向量ν1={v11, v12, …, v1n}) 和Bob (拥有谓词向量ν2={v21, v22, …, v2n}) 两人联合解密。首先, Alice和Bob分别选择随机数a, b∈ ZN, 并公开aν1={av11, av12, …, av1n}, bν2={bv21, bv22, …, bv2n}。对n个不同用户的明文{mi|mi∈GT}, 在ZN中选择随机数ki, 生成密文ci。ci由ci1、ci2、ci3三部分组成:
| $ \left\{ \begin{array}{l} {c_{i1}} = {Z^{a{v_{1i}} + b{v_{2i}} + {k_i}}} \cdot e{(g,{h^2})^{ - r{x_i}}}\\ {c_{i2}} = {({g_1}T_i^{ - 1})^{r{x_i}}}\\ {c_{i3}} = {Z^{a{v_{1i}} + b{v_{2i}} + {k_i}}} \cdot {m_i} \end{array} \right. $ |
SMC (ci):用户将各自的密文ci传送至云服务器上, 由云服务器完成安全多方计算。
| $ \begin{array}{l} {c_1} = \prod\limits_{i{\rm{ = }}1}^n {{c_{i1}}} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,{h^2})^{ - r\sum\limits_{i = 1}^n {{x_i}} }}\\ {c_3} = \prod\limits_{i = 1}^n {{c_{i3}}} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot {m_1}{m_2} \cdots {m_n} \end{array} $ |
云服务器计算得到的最终结果为:
| $ C = \left\{ {{c_1},\left\{ {{c_{i2}}} \right\},{c_3}} \right\} $ |
Dec (C, SK):安全计算的最终结果只能由指定用户Alice和Bob联合解密才可得到, 为了保证Alice和Bob各自私钥不被泄露, 解密过程分为以下步骤:
第1步 Alice先用自己密钥d1i解密密文c1, 得到部分密文C′并将其传送给Bob。其中, 部分密文C′计算过程如下:
| $ \begin{array}{l} {c_1} \cdot \prod\limits_{i = 1}^n {e({c_{i2}},{d_{1i}})} {\rm{ = }}{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,{h^2})^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot \\ \;\;\;\;\;\;\prod\limits_{i = 1}^n {e({g^{(a - {t_i})r{x_i}}},{{(h{g^{s{v_{1i}}}})}^{\frac{1}{{a - {t_i}}}}})} {\rm{ = }}\\ \;\;\;\;\;\;{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,{h^2})^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot e{(g,h)^{r\sum\limits_{i = 1}^n {{x_i}} }} \cdot \\ \;\;\;\;\;\;e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{1i}}} }}{\rm{ = }}\\ \;\;\;\;\;\;{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,h)^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{1i}}} }} \end{array} $ |
第2步 Bob得到Alice发送的部分密文C′后, 再用自己密钥d2i进行解密并将结果反馈给Alice:
| $ \begin{array}{l} C' \cdot \prod\limits_{i = 1}^n {e({c_{i2}},{d_{2i}})} {\rm{ = }}{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,h)^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot \\ \;\;\;\;\;\;e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{1i}}} }} \cdot {\rm{ }}\prod\limits_{i = 1}^n {e({c_{i2}},{d_{2i}})} {\rm{ = }}\\ \;\;\;\;\;\;{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,h)^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot \\ \;\;\;\;\;\;e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{1i}}} }} \cdot \prod\limits_{i = 1}^n {e({g^{(a - {t_i})r{x_i}}},{{(h{g^{s{v_{2i}}}})}^{\frac{1}{{a - {t_i}}}}})} {\rm{ = }}\\ \;\;\;\;\;\;{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,h)^{ - r\sum\limits_{i = 1}^n {{x_i}} }} \cdot e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{1i}}} }} \cdot {\rm{ }}\\ {\rm{ }}\;\;\;\;\;e{(g,h)^{r\sum\limits_{i = 1}^n {{x_i}} }} \cdot e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}{v_{2i}}} }}{\rm{ = }}\\ \;\;\;\;\;\;{Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,g)^{sr\sum\limits_{i = 1}^n {{x_i}({v_{1i}} + {v_{2i}})} }} \end{array} $ |
第3步 对于第2步得到的结果, 不难发现当且仅当
本文方案是以两方解密安全多方计算结果为背景, 当然, 指定联合解密用户的数量可以推广到n(n≥3), 只需在算法的细节上稍作处理即可。具体而言, 在加密算法中, h的幂应由2增加至n(n≥3);在解密算法中, 所有指定联合解密用户依次解密前者的部分密文, 共需n+1步, 这一过程与本文所展示的解密过程并无实质区别。
3 安全性及方案对比 3.1 安全性分析为了证明该方案的安全性, 本文采取文献[14]方法。首先定义两种结构:类密文和类密钥, 它们并不在实际加密中使用而只用于安全性证明。
类密文 g2为群Gp2的生成元, c∈ ZN, {zi∈ ZN},
类密钥 g2为群Gp2的生成元, d∈ ZN, {yi∈ ZN},
正常密钥能解密正常密文和类密文, 正常密文也能被类密钥解密。当使用类密钥去解密类密文时, 会得到一个多余项
基于第1章的假设, 通过证明下列Game的不可区分性, 来证明方案的安全性。
Gamereal中密文与密钥都是正常的, 是实际加密情况;
Game0中密文是类密文, 密钥为正常密钥;
Gamek中前k次密钥查询为类密钥查询;
Gamefinal中所有的密钥查询都为类密钥查询, 密文为类密文。
引理1 若存在多项式时间敌手A满足AdvAGamereal-AdvAGame0=ε, 那么就存在多项式时间敌手β能够以优势ε解决假设1。
证明 挑战假设1, 敌手β将 (G, g, h, X3, T) 作为算法的输入, 随机选择a, {ti}← ZN, 公开参数的设置与算法初始化相同。敌手β将模拟Gamereal和Game0与敌手A进行交互。
在密钥查询阶段, 敌手β能够由主密钥MK通过密钥生成算法产生相应的正常解密密钥。
对于敌手A选择的挑战明文 (m0, m1) 及相应属性 (χ0, χ1), 敌手β把假设1嵌入到挑战密文中去, 以抛掷硬币的方式随机选择加密, 生成密文c*。c*由c1、ci2、c3三部分组成:
| $ \left\{ \begin{array}{l} {c_1} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{(g,{h^2})^{ - \sum\limits_{i = 1}^n {x_i^b} }}\\ \left\{ {{c_{i2}} = {T^{x_i^b(a - {t_i})}}} \right\}\\ {c_{i3}} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot {m_b} \end{array} \right. $ |
如果T∈Gp1, 即T=gr, 密文c*为正常密文。如果T∈Gp1p2, 即T=grg2c, 密文c*为类密文。敌手β将可以利用A的输出以概率ε解决假设1。
引理2 若存在多项式时间敌手A满足AdvAGamek-1-AdvAGamek=ε, 那么就存在多项式时间敌手β能够以优势ε解决假设2。
证明 挑战假设2, 敌手β将 (G, g, h, X3, X1X2, Y2Y3, T) 作为算法的输入, 随机选择a, {ti}← ZN, 公开参数的设置与算法初始化相同。敌手β将模拟Gamek-1和Gamek与敌手A进行交互。
在密钥查询阶段, 当查询次数大于k时, 敌手β由主密钥MK通过密钥生成算法产生相应的正常解密密钥;反之,当查询次数小于k时产生类密钥。当查询次数小于k时, 随机选择s, d← ZN, 类密钥为:
| $ \left\{ {{d_i} = {{(h{g^{s{v_i}}}{{({Y_2}{Y_3})}^{d{y_i}}})}^{\frac{1}{{a - {t_i}}}}}} \right\} $ |
在进行第k次查询时, 敌手β利用T, 并选择随机数, 生成如下密钥:
| $ \left\{ {{d_i} = {{(h{T^{{v_i}}})}^{\frac{1}{{a - {t_i}}}}}} \right\} $ |
如果T∈Gp1p2, 密钥di为正常密钥。如果T∈Gp1p2p3, 即T=gsg2dg3f, 密钥di为类密钥。由于敌手β不清楚N的分解, 所以他只能通过A的输出来解决假设2。
对于敌手A选择的挑战明文 (m0, m1) 及相应属性 (χ0, χ1), 敌手β以抛掷硬币的方式随机选择加密, 生成密文c*。c*由c1、ci2、c3三部分组成:
| $ \left\{ \begin{array}{l} {c_1} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot e{({X_1}{X_2},{h^2})^{ - \sum\limits_{i = 1}^n {x_i^b} }}\\ {c_{i2}} = {({X_1}{X_2})^{x_i^b(a - {t_i})}}\\ {c_{i3}} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot {m_b} \end{array} \right. $ |
令X1X2=grg2c, 则密文c*为类密文。敌手β将可以利用A的输出以概率ε解决假设2。
引理3 若存在多项式时间敌手A满足AdvAGameq-AdvAGamefinal=ε, 那么就存在多项式时间敌手β能够以优势ε解决假设3。
证明 挑战假设2, 敌手β将 (G, g, h, X3, grX2, hY2, T) 作为算法的输入, 随机选择a, {ti}← ZN, 然后公开下列参数PK={g, hY2, g1=ga, {Ti=gti}}。由于敌手A不清楚N的分解, 无法区分hY2和h。所以敌手β将模拟Gameq和Gamefinal与敌手A进行交互。
在密钥查询阶段, 敌手β随机选择s, y′i← ZN, 生成如下类密钥:
| $ \left\{ {{d_i} = {{(h{Y_2}{g^{s{v_i}}}Z_2^{{y_i}^\prime })}^{\frac{1}{{a - {t_i}}}}}} \right\} $ |
令Y2=g2f, Z2=g2d, 设置yi= y′i+f/d。因此, 密钥di为类密钥。
对于敌手A选择的挑战明文 (m0, m1) 及相应属性 (χ0, χ1), 敌手β把假设3嵌入到挑战密文中去, 以抛掷硬币的方式随机选择加密, 生成密文c*。c*由c1、ci2、c3三部分组成:
| $ \left\{ \begin{array}{l} {c_1} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot {T^{ - \sum\limits_{i = 1}^n {x_i^b} }}\\ {c_{i2}} = {({g^r}{X_2})^{x_i^b(a - {t_i})}}\\ {c_{i3}} = {Z^{a{v_1} + b{v_2} + \sum\limits_{i = 1}^n {{k_i}} }} \cdot {m_b} \end{array} \right. $ |
如果T=e(g, h2)r, 密文c*为类密文。如果T∈GT, 密文c*是对随机明文消息加密生成的类密文, 故可以模拟Gamefinal。
敌手β将可以利用A的输出以概率ε解决假设3。
定理1 若假设1~3均为困难问题, 那么该方案达到IND-AH-CPA安全。
证明 若假设1~3均为困难问题, 那么根据上文引理可知, 实际加密情况与Gamefinal是不可区分的。在Gamefinal中, 挑战密文不会泄露关于b的任何信息。因此, 敌手A攻破该方案的优势是可以忽略不计的, 该方案为IND-AH-CPA安全。
3.2 方案对比通过与文献[8]和文献[14]中的谓词方案相比较 (见表 1), 本文构造的支持安全多方同态乘积计算的谓词加密方案, 明显拓展了同态功能, 实现了多用户在云环境下的安全多方计算, 并且在对最终计算结果的解密权限上, 本文方案的控制更加精确, 更能满足实际应用场景。
| 表 1 本文方案和其他谓词方案的对比分析 Table 1 Comparison of SMC-PE scheme with other PE schemes |
本文构造了一个支持安全多方同态乘积计算的谓词加密方案, 具有乘法同态性。与传统安全多方计算加密方案相比, 本文方案通过使用谓词加密, 能够实现对计算结果细粒度更高的访问控制。最后, 分析并证明该方案达到IND-AH-CPA安全; 与此同时, 拓展了同态加密的应用场景。
| [1] | YAO A C. Protocols for secure computations[C]//Proceedings of the 16th Annual Symposium on Foundations of Computer Science. Piscataway, NJ: IEEE, 1982: 160-164. http://ieeexplore.ieee.org/abstract/document/4568388/ |
| [2] | CHOI S G, HWANG K W, KATZ J, et al. Secure multi-party computation of boolean circuits with applications to privacy in on-line marketplaces[C]//CT-RSA 2012: Proceedings of the 2012 Cryptographers' Track at the RSA Conference on Topics in Cryptology, LNCS 7178. Berlin: Springer, 2012: 416-432. http://link.springer.com/chapter/10.1007/978-3-642-27954-6_26 |
| [3] | LOFTUS J, SMART N P. Secure outsourced computation[C]//AFRICACRYPT 2011: Proceedings of the 4th International Conference on Progress in Cryptology, LNCS 6737. Berlin: Springer, 2011: 1-20. http://link.springer.com/10.1007%2F978-3-642-21969-6_1 |
| [4] | 杨高明, 杨静, 张健沛. 聚类的 (α, k)-匿名数据发布[J]. 电子学报, 2011, 39 (8) : 1941-1946. ( YANG G M, YANG J, ZHANG J P. Achieving (α, k)-anonymity via clustering in data publishing[J]. Acta Electronica Sinica, 2011, 39 (8) : 1941-1946. ) |
| [5] | ATALLAH M J, DU W. Secure multi-party computational geometry[C]//Workshop on Algorithms and Data Structures. Berlin: Springer, 2001: 165-179. http://link.springer.com/chapter/10.1007/3-540-44634-6_16 |
| [6] | CACHIN C. Efficient private bidding and auctions with an oblivious third party[C]//CCS 1999: Proceedings of the 6th ACM Conference on Computer and Communications Security. New York: ACM, 1999: 120-127. http://dl.acm.org/citation.cfm?id=319726 |
| [7] | GOLDWASSER S. Multi party computations: past and present[C]//Proceedings of the Sixteenth Annual ACM Symposium on Principles of Distributed Computing. New York: ACM, 1997: 1-6. |
| [8] | KATZ J, SAHAI A, WATERS B. Predicate encryption supporting disjunctions, polynomial equations, and inner products[C]//EUROCRYPT 2008: Proceedings of the 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, LNCS 4965. Berlin: Springer, 2008: 146-162. http://link.springer.com/10.1007/978-3-540-78967-3_9 |
| [9] | WATANABE Y, SHIKATA J. Identity-based hierarchical key-insulated encryption without random oracles[C]//PKC 2016: Proceedings of the 19th IACR International Conference on Practice and Theory in Public-key Cryptography, LNCS 9614. Berlin: Springer, 2016:255-279. http://link.springer.com/chapter/10.1007/978-3-662-49384-7_10 |
| [10] | CLEAR M, TEWARI H, MCGOLDRICK C. Anonymous IBE from quadratic residuosity with improved performance[C]//AFRICACRYPT 2014: Proceedings of the 7th International Conference on Cryptology on Progress in Cryptology, LNCS 8469. Berlin: Springer, 2014: 377-397. http://link.springer.com/chapter/10.1007/978-3-319-06734-6_23 |
| [11] | CLEAR M, MCGOLDRICK C. Policy-based non-interactive outsourcing of computation using multikey FHE and CP-ABE[C]//SECRYPT 2013: Proceedings of the 2013 International Conference on Security and Cryptography. Piscataway, NJ: IEEE, 2013: 1-9. http://ieeexplore.ieee.org/abstract/document/7223196/ |
| [12] | LONGO R, MARCOLLA C, SALA M. Collaborative multi-authority KP-ABE for shorter keys and parameters[EB/OL].[2016-03-10]. https://eprint.iacr.org/2016/262.pdf. |
| [13] | BONEH D, WATERS B. Conjunctive, subset, and range queries on encrypted data[C]//TCC 2007: Proceedings of the 4th Conference on Theory of Cryptography. Berlin: Springer, 2007: 535-554. http://link.springer.com/chapter/10.1007/978-3-540-70936-7_29 |
| [14] | ZHANG M, WANG X, YANG X, et al. Efficient predicate encryption supporting construction of fine-grained searchable encryption[C]//Proceedings of the 20135th International Conference on Intelligent Networking and Collaborative Systems. Piscataway, NJ: IEEE, 2013: 438-442. http://ieeexplore.ieee.org/abstract/document/6630453/ |
| [15] | TAN Z, ZHANG W. A predicate encryption scheme supporting multiparty cloud computation[C]//Proceedings of the 2015 International Conference on Intelligent Networking and Collaborative Systems. Piscataway, NJ: IEEE, 2015: 252-256. http://ieeexplore.ieee.org/abstract/document/7312080/ |
| [16] | LEWKO A, OKAMOTO T, SAHAI A, et al. Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption[C]//EUROCRYPT 2010: Proceedings of the 29th Annual International Conference on Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2010: 62-91. http://link.springer.com/chapter/10.1007/978-3-642-13190-5_4 |
| [17] | BONEH D, GOH E J, NISSIM K. Evaluating 2-DNF formulas on ciphertexts[C]//TCC 2005: Proceedings of the Second International Conference on Theory of Cryptography. Berlin: Springer, 2005: 325-341. http://link.springer.com/10.1007%2F978-3-540-30576-7_18 |




