粒子滤波 (Particle Filter, PF) 算法是一种蒙特卡罗方法和递推贝叶斯估计相结合的新型估计算法,在处理非线性、非高斯系统的状态估计方面具有明显优势,能有效地克服扩展卡尔曼滤波等方法的局限性。由于常规的PF算法没有将最新测量值考虑到重要性密度函数中,容易出现粒子退化现象。减轻粒子退化现象的常用方法是采用重采样方法[1]和选择合适的重要性密度函数。针对重要性密度函数的改进,Carmi等[2]通过构造一个平稳分布为目标的马尔可夫链 (Markov Chain Monte Carlo, MCMC) 来获得重要性采样样本,使样本更加多样化,但是为了保证算法的收敛性,必须进行较多次数的概率转移,计算量也随之增大。Pitt等[3]提出辅助粒子滤波 (Auxiliary Particle Filter, APF),通过引入一个辅助变量将最新量测值考虑进重要性密度函数。当似然函数呈尖峰并且粒子数量不多时,APF算法的滤波性能难以保证。李翠芸等[4]将遗传算法引入到粒子滤波中,代替传统的重采样,提升了粒子的多样性,但算法存在早熟现象。方正等[5]将粒子群优化 (Particle Swarm Optimization, PSO) 与PF算法相结合,提出PSOPF算法,通过模拟寻优的过程不断更新粒子位置,驱动粒子向高似然区域运动,从而减轻了粒子退化的现象; 然而该算法在PSO优化过程中容易导致粒子失去多样性,尤其是似然函数具有双峰甚至多峰时,该算法并不能保证绝大多数粒子向正确的似然峰值移动,其后果是较大的估计的误差甚至出现发散现象。陈志敏等[6]利用辅助因子对粒子的邻域粒子数量进行自适应调整,控制粒子对邻域的影响,减轻局部最优现象,从而提高了估计精度; 然而该文献在确保粒子邻域多样性的同时,并没有保留粒子的预测分布,并没有对似然多峰的情况进行说明和讨论。文献[7]和文献[8]针对常规PSOPF算法容易陷入局部最优、精度降低的问题,引入混沌搜索算法,提升了粒子突破局部极值的能力;然而这样的改进算法只是单纯针对PSO寻优过程,并没有考虑到粒子滤波作为一种数值统计滤波的特殊性,其仍然属于常规PSOPF算法的范畴。
本文在分析常规PSOPF算法不足的基础上,提出一种基于似然分布调整的改进PSOPF (Likelihood Adjustment PSOPF, LA-PSOPF) 算法,在充分利用预测分布信息的基础上,把最新量测值融入到重要性密度函数中,通过PSO优化调整似然分布,增加预测分布和似然分布的重叠区,以有效提高滤波精度和稳定性; 同时引入局部PSO算法策略,即仅对距离最大似然区域较远的粒子进行PSO优化,避免了对大权值粒子的重复运算,这样在保证精度的前提下,能有效减少运算量,增强算法的实时性。
1 常规PSOPF算法与分析PSO算法源于对鸟群捕食行为的研究,是一种群智能算法。PSO算法的数学描述为:在一个n维的搜索空间中,由m个粒子组成的种群x =(x1, x2, …, xm)T,其中第i个粒子位置为xi=(xi, 1, xi, 2, …, xi, n)T,其速度为vi=(vi, 1, vi, 2, …, vi, n)T,个体极值为pi=(pi, 1, pi, 2, …, pi, n)T,种群的全局极值为pg=(pg, 1, pg, 2, …, pg, n)T。然后按照式 (1) 和式 (2) 来更新粒子的速度和位置:
| $ \begin{array}{l} {\boldsymbol{v}}_{i,d}^{k + 1} = \omega \cdot {\boldsymbol{v}}_{i,d}^k + {c_1} \cdot {\mathop{\rm rand}\nolimits} () \cdot ({\boldsymbol{p}}_{i,d}^k - {\boldsymbol{x}}_{i,d}^k)\; + \\ \;\;\;\;\;\;\;\;{c_2} \cdot {\mathop{\rm rand}\nolimits} () \cdot ({\boldsymbol{g}}_{i,d}^k - {\boldsymbol{x}}_{i,d}^k) \end{array} $ | (1) |
| $ {\boldsymbol{x}}_{i,d}^{k + 1} = {\boldsymbol{x}}_{i,d}^k + {\boldsymbol{v}}_{i,d}^{k + 1} $ | (2) |
其中:ω称为惯性权重,决定粒子对当前速度继承的多少,控制算法的开发和探测能力;c1和c2称为学习因子,c1调节粒子飞向个体当前最好位置的步长,c2调节粒子飞向群体当前最好位置的步长;rand () 函数产生 (0, 1) 的随机数。本文采用一种改进的PSO算法,即高斯粒子群优化 (Gaussian PSO, GPSO) 算法[9],该方法利用高斯分布更新粒子的速度,具有更好的收敛性。此时的速度更新方程为:
| $ \begin{array}{l} {\boldsymbol{v}}_{i,d}^{k + 1} = |{\mathop{\rm randn}\nolimits} ()| \cdot ({\boldsymbol{p}}_{i,d}^k - {\boldsymbol{x}}_{i,d}^k) + \\ \;\;\;\;\;\;\;\;|{\mathop{\rm randn}\nolimits} ()| \cdot ({\boldsymbol{g}}_{i,d}^k - {\boldsymbol{x}}_{i,d}^k) \end{array} $ | (3) |
其中:|randn ()|生成正的单位高斯分布随机数。
由此可以看出,PF算法和PSO算法具有共通性,即都是利用粒子的群体行为来获得最优解。基于这一事实,将PSO算法和PF算法相融合是可行的,常规的PSOPF算法步骤如下:
步骤1 初始化。从先验条件概率p(x0) 中采样N个粒子,并设定每个粒子的权值为1/N,得到初始粒子集{(x0i, 1/N)}i=1N。
步骤2 在时刻k,从重要性密度函数采样N个粒子:{xki~q(xk| xk-1i, zk)}i=1N,这里用转移概率密度函数p(xk| xk-1i) 来近似重要性密度函数,得到粒子集:{xk, 0i}i=1N。
步骤3 取得最新量测值zk,定义粒子的适应度函数:
| $ Fitness({\boldsymbol{x}}_k^i) = exp[ - \frac{1}{{2{R_k}}}{({{\boldsymbol{z}}_k} - {\boldsymbol{\hat z}}_{k|k - 1}^i)^2}] $ | (4) |
其中:
1) 对每个粒子,将其适应度值与所经历过的最好位置pi的适应度值进行比较,如果适应度值大,将新的位置作为个体当前的最好位置。
2) 对每个粒子,将其适应度值与群体所经历的最好的位置pg适应度值进行比较,如果适应度值大,将新的位置作为全局当前的最好位置。
3) 当达到某一结束条件时,结束PSO优化。最终得到带权重的粒子集:{(xk, mi, wk, mi)}i=1N,m代表PSO的迭代次数。
步骤4 权重归一化:
| $ w_k^{i*} = w_{k.m}^i/\sum\limits_{i = 1}^N {w_{k,m}^i} $ | (5) |
步骤5 根据式 (6) 计算有效粒子数,并和阈值Nth进行比较,如果Neff < Nth,则进行重采样,将原来的带权值样本映射为等权值样本{(xki, wki**)}i=1N,这里的wki**=1/N。
| $ {N_{eff}} \approx 1/\sum\limits_{i = 1}^N {{{(w_k^{i*})}^2}} $ | (6) |
步骤6 状态估计:
| $ {{\boldsymbol{\hat x}}_k} = \sum\limits_{i = 1}^N {w_k^{i**}{\boldsymbol{x}}_k^i} $ | (7) |
步骤3的第3) 步一般把达到预定的迭代次数作为PSO优化的终止条件。本文算法也采取该种终止条件。
当量测噪声方差很小,似然函数具有单峰且呈尖峰状态时,此时绝大多数的粒子对估计后验概率贡献很微弱,用PSO算法驱动这些无效粒子向高似然区域移动,提高了每个粒子的作用效果。尤其是当粒子数量较少时,常规PSOPF有较好的滤波效果。总的来说,常规PSOPF算法首先通过状态转移方程预测粒子分布,在此基础上,再运用PSO算法结合最新量测值更新粒子的位置和权重,最后得出估计值。其主要过程如图 1所示。
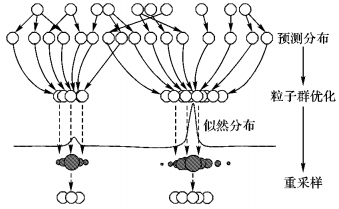
|
图 1 PSOPF算法过程 Figure 1 PSOPF algorithm process |
然而PSOPF算法虽然考虑了最新量测值,但在粒子的寻优移动过程中其预测分布信息丢失,重要性密度函数与真实的后验概率密度函数的偏差仍然较大,所以单纯地通过优化手段将粒子向高似然区域移动并不能很好地提高滤波性能,当似然函数具有双峰甚至多峰时,滤波精度急剧下降甚至出现发散。
2 LA-PSOPF算法针对常规PSOPF算法的不足,本文提出LA-PSOPF算法,保留预测分布信息p(xk| xk-1i),通过PSO过程优化粒子的权值,进而达到调整似然分布的目的。LA-PSOPF算法步骤如下:
步骤1 初始化。同常规PSOPF算法步骤1。
步骤2 在时刻k,从转移概率密度函数中独立采样N个粒子:{xki~p(xk| xk-1i)}i=1N,得到预测分布粒子集:{xk, 0i}i=1N。
步骤3 PSO优化过程开始。
1) 同常规PSOPF算法,依次计算每个粒子的适应度值,得到带权值粒子集{(xk, 0i, wk, 0i)}i=1N。
2) 在粒子集中找出权值小于Tthreshold的粒子,得到原粒子集的子集{(xk, 0j, wk, 0j)|wk, 0j < Tthreshold}j=1Z, 0 < Z≤N,则补集为{(xk, 0h, wk, 0h)}h=1N-Z。
3) 运用PSO算法驱动每个粒子向高似然区域移动。经过m次迭代,得到子集中粒子的最终适应度值为{wk, mj}j=1Z,进而得到全体带权值粒子集:{(xk, 0j, wk, mj)}j=1Z∪{(xk, 0h, wk, 0h)}h=1N-Z={(xk, 0i, wk, 0i)}i=1N。
步骤4 按照式 (5),归一化权值。
步骤5 同常规PSOPF算法,进行重采样,得到等权值样本{(xki, wki**)}i=1N,其中wki**=1/N。
步骤6 同常规PSOPF算法,根据式 (7) 得到估计状态。
从以上步骤可以看出,LA-PSOPF算法仅对粒子的权值进行优化,使多数粒子的权值向最大似然区域靠近,从而提高有效粒子的数量。根据标准PF算法[10]的推导过程,预测分布和似然函数共同决定着粒子的权重;反过来,当预测分布固定时,粒子的权重分布反映出似然分布情况,所以改变粒子的权重分布,实则是调整似然分布。另外当Tthreshold过大时,用于PSO优化过程的粒子变多,虽然提高了精度但运算量比较大;当Tthreshold过小时,运算量降低而精度难以保证。为了获得精度与运算量的平衡,本文假定Tthreshold为粒子数量的函数:
| $ {T_{{\rm{threshold}}}} = f(N) $ | (8) |
f(·) 的具体形式与系统的动态空间模型有关。当N较小时,通过增大Tthreshold的值,使更多粒子参与PSO过程,可以提高精度;当N较大时,在达到精度要求的基础上,可适当减小Tthreshold值,减少运算量。
LA-PSOPF算法过程如图 2所示。
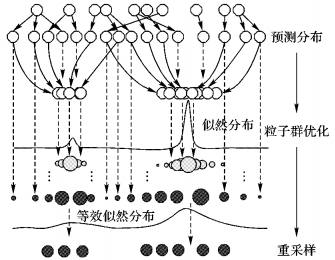
|
图 2 LA-PSOPF算法过程 Figure 2 LA-PSOPF algorithm process |
图 2说明LA-PSOPF算法实则是调整了似然分布,使得原本的似然分布变得平缓一些,尤其是在量测噪声的方差很小,似然函数具有多个尖峰时,其作用效果更加明显; 另一方面,LA-PSOPF算法在保证滤波收敛性的同时确保了粒子的多样性,避免了由于粒子匮乏而出现的发散现象。
3 仿真实验及性能分析实验用计算机配置:处理器为Intel Core i7 3612QM, 主频为2.1 GHz,内存为4 GB,操作系统为Windows 7。实验中采用了文献[11]和[12]中的两种典型的非线性系统模型——非线性非高斯模型和单变量非静态增长模型 (Univariate Nonstationary Growth Model, UNGM),其中非线性非高斯模型似然函数具有单峰特性,UNGM似然函数具有双峰特性; 以及文献[13]中的二维纯方位目标跟踪 (Two-Dimensional Bearing-Only Tracking, 2D-BOT) 模型。对PF、PSOPF和LA-PSOPF算法进行仿真,分别从估计精度、估计稳定性和计算时间三个方面对这三种算法进行比较。
3.1 非线性非高斯模型的仿真该非线性非高斯模型的动态空间方程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_t} = 1 + \sin (w\pi t) + 0.5{x_{t - 1}} + {u_t}}\\ {{y_t} = \left\{ {\begin{array}{*{20}{c}} {0.2x_t^2 + {v_t},\quad \quad t \le 30}\\ {0.5{x_t} - 2 + {v_t},\quad t > 30} \end{array}} \right.} \end{array}} \right. $ | (9) |
其中:ut为服从Gamma分布Γ(k, θ) 的随机噪声,形状参数k=3,尺度参数θ=0.5;vt是均值为零方差为σv2的高斯白噪声。由过程方程可知,当初始值取正数时,量测方程具有单峰,所以本文取x0=1;仿真步数为50。分别在粒子数量为100和500,σv2为0.001和0.000 1条件下进行四组1 000次蒙特卡罗仿真,对于该模型,本文采用式 (10) 确定Tthreshold值:
| $ {T_{{\rm{threshold}}}} = - 0.35*\lg (N/50) + 0.9 $ | (10) |
最终得到表 1的误差统计表和表 2的平均单次滤波时间表。表中均方根误差 (Root Mean Square Error, RMSE) 及其方差计算公式为:
| $ RMSE(\tilde x) = \sqrt {\frac{1}{T}\sum\limits_{t = 1}^T {{{({x_t} - {{\tilde x}_t})}^2}} } $ | (11) |
| $ Var(RMSE) = \frac{1}{M}\sum\limits_{i = 1}^M {\{ RMS{E_i}(\tilde x)} - mean[RMSE(\tilde x)]{\} ^2} $ | (12) |
其中:M为蒙特卡罗仿真次数。图 3是在粒子数量为100,量测噪声方差分别为0.001和0.000 1时的RMSE曲线。
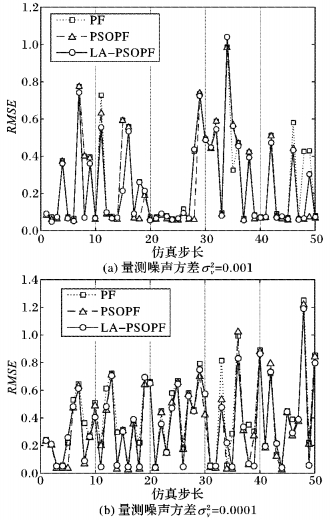
|
图 3 在非线性非高斯模型下三种算法的均方根误差 Figure 3 RMSE of three algorithms under non-linear non-Gaussian model |
由表 1可以看出,三种算法在非高斯条件下,对非线性模型具有比较高的估计精度,体现了PF算法的优势。其中PSOPF算法和LA-PSOPF算法估计精度相近,都略低于PF算法。然而在粒子数量较少的情况下,尤其是量测噪声更小时,LA-PSOPF算法的精度稍低于PSOPF算法,这是由于该模型的预测分布仅包含单峰信息,运用PSO算法同时改变粒子的位置和权重,驱动其向高似然区域移动是合理而有效的。验证了以上对PSOPF算法分析的结论。从表 2可以看出,LA-PSOPF算法的滤波单次滤波时间低于PSOPF算法,当粒子数量增多时更明显。从图 3可以看出,LA-PSOPF算法在该模型下的估计误差比PSOPF算法稍差一些,且在图 3(b)中更加明显,更加直观地显示出了LA-PSOPF算法在单峰似然函数模型下的局限性。
| 表 1 三种算法在非线性非高斯模型下仿真结果数据比较 Table 1 Comparison of simulation results of three algorithms under non-linear non-Gaussian model |
| 表 2 非线性非高斯模型下不同粒子数量时三种算法平均单次滤波时间比较 Table 2 Comparison of three algorithms with different number of particles on average single filter time under non-linear non-Gaussian model |
UNGM模型具有强非线性,其状态空间方程为:
| $ \left\{ \begin{array}{l} {x_t} = 0.5{x_{t - 1}} + \frac{{25{x_{t - 1}}}}{{1 + x_{t - 1}^2}} + 0.8\cos (1.2(t - 1)) + {u_t}\\ {y_t} = \frac{{x_t^2}}{{20}} + {v_t} \end{array} \right. $ | (13) |
其中:ut和vt为相互独立的高斯白噪声 (t=1, 2, …, T),且ut~Ν(0, σu2),vt~Ν(0, σv2);初始状态为x0~N(μ0, σ02)。本文设定μ0=1,σ02=1。单次仿真时间T=100。在粒子数量N、过程噪声方差σu2和量测方差σv2不同的情况下,比较以上三种算法估计的均方误差 (RMSE) 及其方差和单次滤波的平均时间,蒙特卡罗仿真次数为1 000。对于该模型,本文采用式 (14) 确定Tthreshold值:
| $ {T_{{\rm{threshold}}}} = - 0.3*\lg (N/50) + 0.7 $ | (14) |
仿真结果如图 4和表 3~4所示,其中相对误差是指相对于PF算法的误差相对值,等于其他两种算法的均方误差值与PF算法的均方误差值的比值。图 4是粒子数量为200,在噪声方差为10,量测方差分别为0.1和0.01时,三种算法的均方根误差曲线。
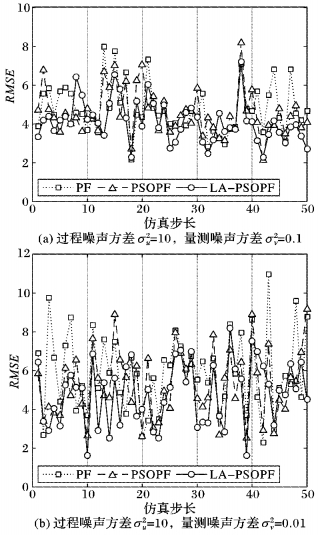
|
图 4 UNGM下三种算法的均方根误差 Figure 4 RMSE of three algorithms under UNGM |
| 表 3 三种算法的UNGM仿真结果数据比较 Table 3 Comparison of simulation results of three algorithms under UNGM |
| 表 4 UNGM下不同粒子数量的三种算法平均单次滤波时间比较 Table 4 Comparison of three algorithms with different number of particles on average single filter time under UNGM |
表 3是在不同的噪声方差和不同的粒子数量条件下,三种算法用UNGM仿真的数据比较。从表 3可看出,三种算法的估计误差和估计误差方差都随着粒子数量的增加而减小,这符合PF算法的一般规律。通过比较相对误差可得,对于PSOPF算法和LA-PSOPF算法,粒子数量越少,其估计的精度相对于PF算法越好,这是由于PSO算法优化了粒子的位置,增强了每个粒子的作用效果。进一步比较可以看出,当量测噪声方差相对于过程噪声方差更小时,LA-PSOPF算法相对于PF和LA-PSOPF算法的估计精度越高,稳定性也越好,因预测分布包含了双峰信息被保留,似然分布被调整而变得“平缓”,增加了与预测分布的重叠区,提高了粒子的利用率,这验证了算法分析的结论, 同时,从图 4分析能也能得到一致的结论。对于PSOPF算法,当粒子数量为200时,随着过程噪声减小,其滤波性能相对于另外两种算法急剧下降,因为PSOPF算法舍弃了预测分布的信息,而过程噪声越小预测分布信息的置信度越高。LA-PSOPF算法集中了另外两种算法的优点,因此具有较好的估计性能。
表 4是三种算法在粒子数量分别为50、200和500时平均单次滤波时间的比较。从表 4可看出,LA-PSOPF算法滤波时间少于PSOPF算法,且都多于PF算法,这也是PSO与PF算法相结合的最大缺点。结合表 3和表 4可知,当粒子数量为500,且量测噪声方差相对较大时,PSOPF与LA-PSOPF的相对误差接近于1,失去了优势。当量测噪声方差相对较小时,LA-PSOPF算法的估计精度和稳定性都优于其他两种算法,相对于PSOPF,其在时间上的优势变得明显。
3.3 2D-BOT模型的仿真2D-BOT模型用于被动跟踪系统中,由于其隐蔽性好、抗干扰性强,历来是研究的热点和难点。该模型仅通过方位角度来对目标进行跟踪,式 (15) 是其在直角坐标系下的状态转移方程和观测方程:
| $ \left\{ \begin{array}{l} {\boldsymbol{x}}(k) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}}(k - 1) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} w}}\left( {k - 1} \right)\\ z(k) = \arctan \frac{{{y_p}(k) - {y_z}}}{{{x_p}(k) - {x_z}}} + v(k) \end{array} \right. $ | (15) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{c}} 1&{dt}&0&0\\ 0&1&0&0\\ 0&0&1&{dt}\\ 0&0&0&1 \end{array}} \right]\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[ {\begin{array}{*{20}{c}} {0.5d{t^2}}\\ {dt}\\ 0\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ {0.5d{t^2}}\\ {dt} \end{array}} \right] $ |
其中: Φ =为状态转移矩阵;Γ为系统噪声驱动矩阵。令系统噪声w(k)=[wx(k), wy(k)]T为零均值高斯白噪声,方差为σu2;量测噪声v(k) 也是均值为零的高斯白噪声,方差为σv2,因此该模型的似然函数具有多峰特性。设采样时间间隔dt=1,目标的初始状态x (0)=[0.5, 0.3, 0.5, 0.3]T。设单次仿真步数为50,进行两组100次独立仿真。在粒子数量为100,σu2=0.000 3的条件下改变σv2,得到的仿真结果如表 5所示。
| 表 5 在2D-BOT模型下三种算法跟踪性能比较 Table 5 Tracking performance comparison of three algorithms under 2D-BOT model |
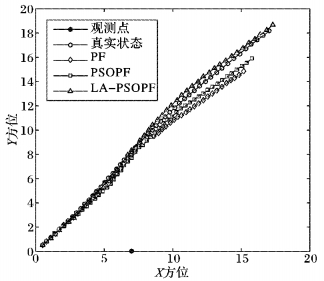
从表 5可以看出,当粒子数为100时,LA-PSOPF算法在跟踪精度和跟踪的稳定性方面都优于PF和PSOPF算法。在运算时间方面优于PSOPF算法。图 5是其中一次目标跟踪结果,图中LA-PSOPF算法较好地实现了目标跟踪。
|
图 5 三种算法的跟踪效果 Figure 5 Tracking results of three algorithms |
综合上述仿真实验可知,在系统似然函数具有双峰或者多峰特性,且量测噪声方差相对较小时,LA-PSOPF算法相对于PF和PSOPF算法具有较好的估计性能,运算时间介于两者之间。
4 结语本文通过分析常规PSOPF算法存在的问题,提出一种基于似然分布调整的LA-PSOPF算法,在保留预测分布的基础上,运用PSO算法调整权重分布,达到调整似然分布的目的,增加了预测分布和似然分布的重叠区,提高了有效粒子的数量,进而提升了滤波性能; 同时, 本文采用局部PSO优化算法策略,缩减PSO种群规模,达到精度与运算量的平衡。非线性非高斯模型、UNGM和2D-BOT模型的仿真结果表明了当量测误差较小, 似然函数具有多峰值时,LA-PSOPF算法的滤波精度和稳定性都优于PF算法和PSOPF算法,同时运算时间少于PSOPF算法; 但是,本文算法目前仅对粒子数量较少,量测噪声方差相对于过程噪声方差很小的系统有较好的滤波效果,下一步主要工作就是对本文算法进行改进,增强其鲁棒性,同时进一步改进简化运算,提升其运算速度。
| [1] | GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F: Radar and Signal Processing, 1993, 140 (2) : 107-113. doi: 10.1049/ip-f-2.1993.0015 |
| [2] | CARMI A, SEPTIER F, GODSILL S J. The Gaussian mixture MCMC particle algorithm for dynamic cluster tracking[C]//Proceedings of the 200912th International Conference on Information Fusion. Piscataway, NJ: IEEE, 2009:2454-2467. http://www.sciencedirect.com/science/article/pii/S0005109812003561 |
| [3] | PITT M K, SHEPHARD N. Filtering via simulation: auxiliary particle filters[J]. Economics Papers, 1999, 94 (446) : 1042-1043. |
| [4] | 李翠芸, 姬红兵. 新遗传粒子滤波的红外弱小目标跟踪与检测[J]. 西安电子科技大学学报, 2009, 36 (4) : 619-623. ( LI C Y, JI H B. IR dim target tracking and detection based on new genetic particle filter[J]. Journal of Xidian University, 2009, 36 (4) : 619-623. ) |
| [5] | 方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策, 2007, 22 (3) : 273-277. ( FANG Z, TONG G F, XU X H. Particle swarm optimized particle filter[J]. Control and Decision, 2007, 22 (3) : 273-277. ) |
| [6] | 陈志敏, 薄煜明, 吴盘龙, 等. 一种新型自适应粒子群优化粒子滤波算法及应用[J]. 应用科学学报, 2013, 31 (3) : 285-293. ( CHEN Z M, BO Y M, WU P L, et al. Novel particle filtering based on adaptive particle swarm optimization and its application[J]. Journal of Applied Sciences, 2013, 31 (3) : 285-293. ) |
| [7] | 李明, 逄博, 年福忠. 基于混沌的PSO粒子滤波算法[J]. 计算机工程, 2012, 38 (8) : 134-136. ( LI M, PANG B, NIAN F Z. Particle swarm optimization particle filtering algorithm based on chaotic[J]. Computer Engineering, 2012, 38 (8) : 134-136. ) |
| [8] | 王尔申, 庞涛, 曲萍萍, 等. 基于混沌的改进粒子群优化粒子滤波算法[J]. 北京航空航天大学学报, 2016, 42 (5) : 885-890. ( WANG E S, PAGN T, QU P P, et al. Improved particle filter algorithm based on chaos particle swarm optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (5) : 885-890. ) |
| [9] | KROHLING R A. Gaussian swarm: a novel particle swarm optimization algorithm[C]//Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems. Piscataway, NJ: IEEE, 2005:372-376. http://ieeexplore.ieee.org/abstract/document/1460443/ |
| [10] | 王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37 (8) : 1679-1694. ( WANG F S, LU M Y, ZHAO Q J, et al. Particle filter algorithm[J]. Chinese Journal of Computers, 2014, 37 (8) : 1679-1694. ) |
| [11] | LI L Q, JI H B, LUO J H. The iterated extended Kalman particle filter[C]//Proceedings of the 2005 IEEE International Symposium on Communications and Information Technology. Piscataway, NJ: IEEE, 2005: 1213-1216. |
| [12] | 陈志敏, 薄煜明, 吴盘龙, 等. 基于新型粒子群优化粒子滤波的故障诊断方法[J]. 计算机应用, 2012, 32 (2) : 432-435. ( CHEN Z M, BO Y M, WU P L, et al. Fault diagnoses based on new particle swarm optimization particle filter[J]. Journal of Computer Applications, 2012, 32 (2) : 432-435. ) |
| [13] | 吴将, 朱志宇. 基于改进SIRF的二维纯方位目标跟踪[J]. 弹箭与制导学报, 2014, 34 (3) : 133-136. ( WU J, ZHU Z Y. Two-dimensional bearings-target tracking based on improved SIRF[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34 (3) : 133-136. ) |




