复杂网络普遍存在着“同一社区内节点连接紧密、不同社区间节点连接稀疏”的社区结构特性[1]。社区是从中观视角研究复杂网络的一种高效手段, 可以充分利用社区这一特点研究网络的拓扑结构、物理意义和功能行为。2004年, Newman等[2]提出了一个用于刻画网络社区结构优劣的量化标准, 被称之为模块度Q。模块度Q给出了社区结构的清晰定义, 最初是为评价社区发现结果的优劣, 并在实际应用中获得了很大的成功, 同时以模块度Q为目标函数的模块度优化方法也成为复杂网络社区发现领域的主流方法之一。最简单的模块度优化方法是找出一个网络所有可能的划分, 从中选择拥有最大Q值的划分作为最后的社区发现结果, 但这是一个NP难问题[3], 因为一个网络可以拥有的划分数目是节点数目的指数量级。因此一些基于启发式策略的模块度优化算法被提出, 主要有基于贪心策略算法[4-5]、基于层次聚类的算法[6-7], 以及融合多种策略 (贪心策略、局部优化、层次聚类等) 的算法[8-10]。在这些算法中, 融合了贪心策略和层次聚类策略的鲁汶算法 (Louvain Method, LM)[8]以其时间复杂度低且具有高质量的社区发现结果, 得到了许多学者的认可, 被著名社区挖掘专家Fortunato[11]评为当前性能最佳的模块度优化算法, 另外复杂网络分析软件Gephi中的社区发现子模块也采用了该算法。
LM是迭代算法。在每次迭代中, 算法首先在每个节点的邻居区域内局部优化模块度Q并获得一个社区划分结果, 然后将得到的每个社区作为一个超级节点、社区间的连接作为加权边, 构建一个新的网络并作为下次迭代的输入; 不断迭代上述两步, 直至Q值不再增加为止。尽管LM是很优秀的算法, 但其依然有改进的空间。文献[12]通过降低每次迭代的结束条件, 在略微牺牲社区发现结果精度的基础上可以较大幅度地缩短算法的运行时间; 文献[13]在原算法社区发现结果的基础上, 加入细化提纯过程以进一步提升社区发现结果的精度; 文献[14]在原算法中加入了并行策略以缩短算法的运行时间; 文献[12, 15]综合考虑了网络的其他属性重新定义了边的权值, 然后应用LM进行社区甄别, 从而使社区发现的结果更符合实际情形。本文对LM的改进如下:
1) LM需要频繁地计算节点合并以及节点离开原属社区后Q的增益, 但是有关模块度Q的现有研究中只有第一类增益的计算方法, 对于第二类增益只能通过第一类增益的计算方法间接地计算。本文给出了一种节点离开原属社区后Q增益的计算方法, 完善了该领域的理论研究。
2) LM具有高质量的社区发现结果, 部分原因是因为其通过算法运行的中间结果提供了层次化的社区结构。存储算法运行的中间结果, 使得LM对存储空间的需求较高, 约为其他相近算法的20倍[8]。本文在LM中引入了分离孤立节点的改进策略。实验结果表明, 与原算法相比,改进后的算法不仅对存储空间的需求大幅减小, 而且其运行时间也得到了进一步的缩减。
1 模块度Q及其增益的计算方法 1.1 模块度Q模块度Q有两种等价的定义[5], 分别是基于网络邻接矩阵的定义和基于网络社区连接矩阵的定义, 这里只给出第二种定义。
定义1 网络G=(V, E, w)。其中:V为节点集合, E为边集合, w为边权值的映射函数, 即w为V×V→ R的映射函数, ∀{u, v}∈E, w(〈u, v〉)≠0;∀{u, v}∉E, w(〈u, v〉)=0。在无向网络中, 每条边被存储两次, 即若节点u和节点v之间存在一条边, 则有w(〈u, v〉)=w(〈v, u〉)=该边的权值。将边〈u, v〉的权值简记为wu, v(或wv, u)。令2m=∑wu, v, 表示网络中所有边的权值之和的两倍。
定义2 假设网络G被划分为k个社区, 定义k阶对称矩阵E (eij) 为G的社区连接矩阵, 其中eij等于所有连接i社区中节点和j社区中节点的边的权值之和, 即
由上可知eii等于i社区中所有边的权值之和的两倍, 并且∑eij=2m。令
| $ Q = \sum\limits_{i = 1}^k {\left( {\frac{{{e_{ii}}}}{{2m}} - {{\left( {\frac{{{a_i}}}{{2m}}} \right)}^2}} \right)} $ | (1) |
Q值越大意味着在网络的社区连接矩阵中, 其对角线上的元素之和占矩阵中所有元素之和的比例越大, 对于整个网络而言, 表现为社区内部中边的权值之和占网络中所有边的权值之和的比例越大, 即“同一社区内节点连接紧密、不同社区间节点连接稀疏”, 也就是社区结构越明显。模块度Q给出了社区结构的清晰定义, 并且其取值区间为[-0.5, 1]。
1.2 Q增益的计算方法| $ \boldsymbol{A} = \left( {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}& \ldots &{{e_{1,n - 1}}}&{{e_{1n}}}\\ {{e_{21}}}&{{e_{22}}}& \ldots &{{e_{2,n - 1}}}&{{e_{2n}}}\\ \vdots & \vdots &{}& \vdots & \vdots \\ {{e_{n - 1,1}}}&{{e_{n - 1,2}}}& \ldots &{{e_{n - 1,n - 1}}}&{{e_{n - 1,n}}}\\ {{e_{n,1}}}&{{e_{n,2}}}& \ldots &{{e_{n,n - 1}}}&{{e_{n,n}}} \end{array}} \right) $ |
| $ \begin{array}{l} \boldsymbol{B} = \\ \left( {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}&\ldots&{{e_{1,n-2}}}&{{e_{1,n-1}}+{e_{1n}}}\\ {{e_{21}}}&{{e_{22}}}&\ldots&{{e_{2,n-2}}}&{{e_{2,n-1}}+{e_{2,n}}}\\ \vdots&\vdots&{}&\vdots&\vdots\\ {{e_{n-2,1}}}&{{e_{n-2,2}}}&\ldots&{{e_{n-2,n-2}}}&{{e_{n-2,n-1}}+{e_{n-2,n}}}\\ {{e_{n-1,1}}+{e_{n,1}}}&{{e_{n-1,2}}+{e_{n,2}}}&\ldots&{{e_{n-1,n-2}}+{e_{n,n-2}}}&{{e_{n-1,n-1}}+{e_{n-1,n}}+{e_{n,n-1}}+{e_{n,n}}} \end{array}}\right) \end{array} $ |
| $ \begin{array}{l} \Delta {Q_{{\rm{merge}}}} = {Q_\boldsymbol{B}} - {Q_\boldsymbol{A}} = \\ \frac{1}{{2m}}\left[ {\left( {{e_{n - 1,n}} + {e_{n,n - 1}} + \sum\limits_{i = 1}^n {{e_{ii}}} } \right) - \frac{{{{\left( {{a_{n - 1}} + {a_n}} \right)}^2} + \sum\limits_{i = 1}^{n - 2} {a_i^2} }}{{2m}}} \right] - \\ \frac{1}{{2m}}\sum\limits_{i = 1}^n {\left( {{e_{ii}} - \frac{{{a_i}^2}}{{2m}}} \right)} = \frac{1}{{2m}}\left( {{e_{n - 1,n}} + {e_{n,n - 1}} + \frac{{2 \cdot {a_{n - 1}}{a_n}}}{{2m}}} \right) = \\ \frac{1}{m}\left( {{e_{n - 1,n}} - \frac{{{a_{n - 1}} \cdot {a_n}}}{{2m}}} \right) \end{array} $ | (2) |
设某时刻网络有n个社区, A为其社区连接矩阵。合并第n-1个社区和第n社区, 即在A中将第n行 (列) 元素加到第n-1行 (列), 记合并后网络的社区连接矩阵为B, 则合并后Q增益的计算方法如式 (2) 所示。因为社区编号相互独立且是人为设定的, 所以在计算任意两个社区合并后Q的增益时, 可以将这两个社区的编号分别记为n-1和n, 即式 (2) 可以计算任意两个社区合并后Q的增益。式 (2) 也可以计算任意两组节点 (包括两个节点) 合并后Q的增益, 只需将这两组节点视为两个社区。
记节点v所属社区为cv, cv′表示在cv中去除v以及与v相连的边后形成的社区, 此时将v视为只含有一个节点的社区, 按照式 (2) 逆向推导, 则v离开cv后Q增益的计算方法如式 (3) 所示:
| $ \Delta {Q_{{\rm{depart}}}} = \frac{1}{m}\left( {\frac{{{a_v} \cdot \left( {{a_{{c_v}}} - {a_v}} \right)}}{{2m}} - {e_{v,{c_v}^\prime }}} \right) $ | (3) |
其中:av为节点v的度;acv为社区cv中所有节点的度求和;ev, cv′为连接v节点与社区cv′中节点的边的权值之和。同样式 (3) 也可以计算一组节点离开原属社区后Q的增益, 只需将这组节点视为一个社区, 此时av为这组节点的度求和。
2 基于孤立节点分离策略的改进LM算法 2.1 符号说明1) Gl=(Vl, El, wl):算法第l次迭代的生成网络, 同时也是第l+1次迭代的输入网络, 简称为第l层网络, 在具体实现时采用邻接链表存储; wl(i, j)/wl(j, i) 表示Gl中连接节点i和节点j的边的权值。G0=(V0, E0, w0) 为初始网络。因为LM是迭代算法, 其第l次迭代生成的社区是第l+1次迭代的输入节点, 所以下文中的节点和社区具有相同的含义, 不再特殊说明。
2) Il:Gl中孤立节点的集合。
3) 为了方便计算Q的增益以及每一层网络的Q值, 依据式 (1)~(3), 为每个社区设置三个参数, 分别是:1) in,社区内部所有边的权值之和的两倍; 2) all,社区内部所有节点的度之和; 3) cid,社区标识号, 算法结束后, 各层网络中的社区由参数cid连接形成树形层次网络 (即层次化的社区发现结果)。“.”表示引用关系, 例如Vl[i].all表示第l层网络中编号为i的社区 (节点) 中所有节点的度之和。需要注意的是, 在计算Q的增益时, 不需要参数in。
4) Nl(i)={j|j∈Vl, (i, j)∈El}:第l层网络中节点i的邻居节点集合。
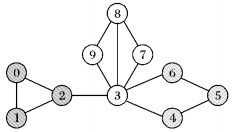
5) AdjionCommunity:节点的邻接社区哈希表, 由键值对[Cid, Weight]组成, 其中Cid是社区的标识号, Weight为该节点与Cid社区间所有连边的权值之和。图 1为拥有3个社区的一个网络, 若其中每条边的权值为1, 记3个社区的标识号从左到右依次为1、2、3, 则节点3的邻接社区哈希表为:{(1, 1);(2, 3);(3, 2)}。
|
图 1 拥有3个社区的网络 Figure 1 Network with three communities |
基于孤立节点分离策略的改进鲁汶算法 (Louvain Method+, LM+) 的主要流程如算法1所示。
算法1 Louvain Method+。
输入:初始网络G0=(V0, E0, w0)。
输出:连通网络集合G=(G1, G2, …, Gl);
孤立节点集合I=(I0, I1, …, Il)。
局部变量:l、t分别标识迭代的次数和每次迭代中对连通网络的扫描次数, 初始值为0;increase标识一次遍历中是否有节点发生移动, 初始值为true。
1) While (true)
2) l←l+1;
3) Init (Gl-1)
4) While increase do
5) increase←false;
6) t←t+1;
7) Foreach i of Vl-1 do
8) 〈ΔQdepart|ΔQmaxEnter|MaxCid〉←getΔQ (Nl-1(i))
9) if (ΔQdepart+ΔQmaxEnter>0)
10) increase←true;
11) Vl[i.cid].all←Vl[i.cid].all-i.all
12) Vl[MaxCid].all←Vl[MaxCid].all+i.all
13) if (Vl[i.cid].all= =0)
14) Vl.Delete(i.cid);
15) i.cid←MaxCid;
16) if (t= =1)
17) Return;
18) Foreach i of Vl-1 do
19) Vl[i.cid].in←Vl[i.cid].in+i.in;
20) Foreach j of Nl-1(i) do
21) if (i.cid= = j.cid)
22) Vl[i.cid].in←Vl[i.cid].in+wl-1(i, j);
23) else
24) wl(i.cid, j.cid)←wl(i.cid, j.cid)+wl-1(i, j)
25) G.Add(Gl)
LM+是迭代算法, 第l次迭代中, 算法的输入为第l-1层网络Gl-1, 输出为Gl-1中的孤立节点集合Il-1和第l层网络Gl。在每次迭代中, 首先通过初始化函数Init筛选出Il-1, 并用每一个非孤立节点 (连通节点) 建立的一个社区。第4)~15) 步循环遍历Gl-1中的连通节点, 直至不再有节点的社区发生变化; 在每次遍历中, 对每一个节点首先通过Q增益计算函数getΔQ计算出该节点离开原属社区后Q的增益ΔQdepart以及进入邻居社区能产生的最大“进入增益”ΔQmaxEnter, 记ΔQmaxEnter对应的邻接社区编号为MaxCid; 当ΔQdepart+ΔQmaxEnter>0, 即节点离开原社区并进入MaxCid社区后, 将给全网络的Q带来正的最大增益, 则移动节点; 第11)~12) 步表示节点离开原社区以及进入MaxCid社区后, 原社区与MaxCid社区all参数的更新方法; 当某个社区中的所有节点都移动到了其他社区, 则删除该社区 (第13)~14) 步)。第18)~24) 步通过遍历1次Gl-1中的连通节点, 完成Gl边集合的更新以及Gl中每个节点参数in的更新。需要注意的是, 每次迭代中对连通节点的最后一次遍历不会发生节点的移动操作, 所以若某次迭代中对输入网络的连通节点只遍历了1次, 则表明网络中所有的节点都不会再移动, 此时算法终止 (第16)~17) 步)。
LM+中使用了两个功能函数。初始化函数Init通过扫描一次Gl-1中的节点, 筛选出其中的孤立节点, 并将这些孤立节点添加至Il-1, 然后用每一个非孤立节点建立一个社区 (即Gl中的初始节点)。Q增益计算函数getΔQ遍历1次节点i的邻居节点集合Nl-1(i), 得到i的邻接社区哈希表, 然后利用式 (2) 计算出i离开原属社区后Q的增益, 利用式 (3) 分别计算出孤立节点i进入每个邻居社区后Q的增益, 并从中选出最大“进入增益”ΔQmaxEnter, 最后用MaxCid标识ΔQmaxEnter对应的邻居社区编号。
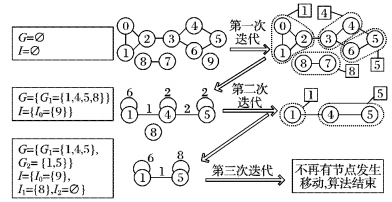
图 2为LM+的一个运行实例, 其中左侧方框中注明了每次迭代开始 (上次迭代结束) 时, 连通网络集合G和孤立节点集合I的元素值。因为篇幅所限, 对每一个连通网络, 图中只列出其节点集合, 未列出边集合。另外初始网络中可能有孤立节点, 所以在最后的结果中, 集合I比集合G多一个元素。
|
图 2 LM+运行实例 Figure 2 Illustration of LM+ |
LM+的两个功能函数如下:
In it (Gl-1)
Foreach i of Vl-1 do
If (Nl-1(i).count= =0)
Il-1.Add(i);
Vl-1.Delete(i);
else
Gl.Add(i);
Gl[i].cid←i.cid;
Gl[i].all←i.all;
Gl[i].in←0;
I.Add(Il-1);
getΔQ (Nl-1(i))
Foreach j of Nl-1(i) do
J←j.cid;
if (AdjionCommunity.Contain(J))
AdjionCommunity[J]←AdjionCommunity[J]+wl-1(i, j);
else
AdjionCommunity.Add(J, wl-1(i, j));
Foreach KeyValuePair (Cid, Weight) do
if (Cid= =i.cid)
else
if (ΔQmaxEnter < ΔQEnter)
ΔQmaxEnter←ΔQEnter;
MaxCid←Cid
Return 〈ΔQdepart| ΔQmaxEnter|MaxCid〉;
2.3 LM+复杂度分析设初始网络中节点数目为n, 节点度的最大值为k, 记每次迭代中输入网络的规模与初始网络的规模相同 (其实随着迭代的进行, 输入网络的规模越来越小), 迭代总次数为c1, 每次迭代中扫描连通节点的次数为c2。大量实验结果表明c1、c2是与网络规模无关的常数[8, 12-15], 并且它们的取值较小。所以LM+的时间复杂度为:
| $ {c_1} \cdot (n + {c_2} \cdot n \cdot k + n \cdot k) = O(n \cdot k) $ |
当为稀疏网络即节点的度较小时, LM+为线性时间复杂度O(n),LM+算法的空间复杂度也为O(n·k), 在稀疏网络上为O(n)。
3 实验对比分析这里需要明确, LM+和LM的最终运行结果完全相同, 它们的时空复杂度也相同, 本文的改进策略只是进一步缩减了原算法对时间及空间资源的需求。表 1是LM+和LM在银行客户交易网络上运行时过程结果的对比, 表中分别给出了每次迭代时两种算法输入、输出网络的规模 (节点个数)。LM+每次迭代时将输入网络的孤立节点提前分离出去, 只令其中连通节点实际参与迭代过程, 使得后续迭代中输入网络的规模大幅减小, 进而可缩减算法对时间、空间资源的需求。比如第4次迭代时, LM+中实际参与迭代的节点为798个, 而LM中为38 776个节点, 这38 776个节点中主要包含的是前几次迭代产生的36 748+1 212+18=37 978个孤立节点。
| 表 1 LM+和LM银行客户交易网络运行过程结果对比 Table 1 Comparison of operating results on bank customer trading network for LM+ and LM |
尽管LM为线性空间复杂度, 但相对于其他算法, 其对存储空间的需求较高, 是其他相近算法的20倍, 这是因为LM需要存储中间迭代过程产生的结果, 有时甚至需要存储每次迭代中每一次扫描后的结果。通过中间迭代过程产生的结果, LM提供了层次化的社区发现结果。层次化的社区结构很好地体现了复杂网络的自相似性和层次特性, 为后续研究网络的相关特性提供了很重要的信息。另外,模块度优化算法普遍存在着“分辨率限制问题”[16]——算法为了使模块度达到最大, 会将一些较小旳社区合并为较大的社区, 导致无法发现那些较小的社区。通过层次化的社区结构, LM提供了多粒度的社区发现结果, 是解决分辨率限制问题一种有效手段。
LM+在存储中间迭代过程产生的结果时, 将孤立节点和连通节点分开存储, 使得每次迭代产生的孤立节点只存储1次, 避免了对这类节点的重复存储, 进而大幅缩减了其对存储空间的需求。这里采用空间压缩比量化LM+相对于LM对存储空间需求的缩减程度。
定义3 空间压缩比=(LM存储节点数-LM+存储节点数)/LM存储节点数。
因为复杂网络是稀疏网络, 且随着算法的运行, 逐次迭代的输出网络中社区结构越明显即边越少, 因此在计算存储空间时, 只计入网络的节点个数, 不计入边数目。在统计每次迭代中需要存储的节点数目时, 只计入本次迭代最终结果的节点数目, 不计入中间扫描过程产生结果的节点数目。
表 2展示了不同网络上两种算法在运行时间和空间上的对比 (两种算法的社区发现结果相同, 不再罗列), 可以看出LM+在处理真实网络时更具优势。首先如图 3所示, LM+和LM一样, 不同的节点输入顺序对应有不同的社区发现结果和相异的运行时间, 为此在表 2中, 每个网络的运行结果是100次不同节点输入顺序下的平均结果。另外在LM+中, 每次迭代时分离孤立节点的操作集成在初始化函数中, 不会带来对输入网络的额外扫描, 所以在全连通网络上, 两种算法的运行时间几乎相同。诚然, 在一个系统的全数据集上或者时间跨度很大的情况下, 建模出的网络连通性较高, 孤立社区较少, 此时LM+的改进效果不明显。但全数据的处理必将导致很高的时间、空间需求, 并且因为其忽略了时间属性, 无法对系统进行更全面的研究。社区进化的研究是复杂网络社区研究领域的一个重要分支[19], 考虑时间属性研究社区的进化需频繁地在时间跨度较小的网络上进行社区甄别, 此时LM+对原算法的改进策略将有很高的价值。
| 表 2 不同网络上的运行结果对比 Table 2 Comparison of operating results on different networks |
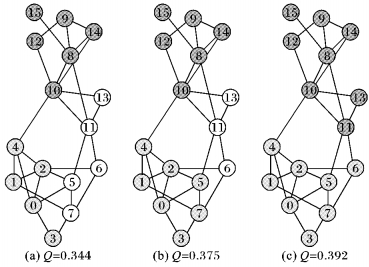
LM+同LM一样, 对节点属于顺序敏感, 不同的节点输入顺序对应有不同的社区发现结果和相异的算法运行时间, 但是不同的社区发现结果之间的差异较小, 各个结果的Q值落会在一个以网络实际拥有的最大Q值为中心、半径比较小的一个区间上。在节点输入顺序随机的情况下, 文本在图 3所示的网络上运行了1 000次LM+, 产生了图中所示的3种不同结果, 这3种结果从左到右分别发生了9次、65次和926次, 可以看出, 这3种结果之间的差异较小 (Q值都在0.35左右)。
|
图 3 同一网络的不同社区发现结果 Figure 3 Different results of communities detected on a network |
本文首先推导出了网络中的节点离开原属社区后模块度Q增益的计算方法, 完善了关于复杂网络模块度Q的理论研究; 然后通过在LM中引入分离孤立节点的策略, 克服了原算法对存储空间需求高的缺点, 并进一步缩减了算法的运行时间。后续工作中, 将重点研究节点输入顺序对LM+的影响, 以改进其对节点输入顺序敏感的缺点。
| [1] | GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99 (12) : 7821-7826. doi: 10.1073/pnas.122653799 |
| [2] | NEWMAN M E, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2004, 69 (2 Pt 2) : 026113. |
| [3] | BRANDES U, DELLING D, GAERTLER M, et al. On finding graph clusterings with maximum modularity[C]//Proceedings of the 33rd International Conference on Graph-Theoretic Concepts in Computer Science. Piscataway, NJ: IEEE, 2007:121-132. |
| [4] | NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2004, 69 (6 Pt 2) : 066133. |
| [5] | CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2004, 70 (6 Pt 2) : 066111. |
| [6] | DUCH J, ARENAS A. Community detection in complex networks using extremal optimization[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2005, 72 (2 Pt 2) : 027104. |
| [7] | LV Z, HUANG W. Iterated tabu search for identifying community structure in complex networks[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2009, 80 (2 Pt 2) -026130. |
| [8] | BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics Theory & Experiment, 2008, 2008 (10) : 155-168. |
| [9] | LIU X, MURATA T. Advanced modularity-specialized label propagation algorithm for detecting communities in networks[J]. Physica A: Statistical Mechanics & Its Applications, 2009, 389 (7) : 1493-1500. |
| [10] | GACH O, HAO J K. A memetic algorithm for community detection in complex networks[C]//PPSN 2012: Proceedings of the 12th International Conference on Parallel Problem Solving from Nature. Berlin: Springer, 2012:327-336. |
| [11] | LANCICHINETTI A, FORTUNATO S. Community detection algorithms: a comparative analysis[J]. Physical Review E: Statistical, Nonlinear and Soft Matter Physics, 2009, 80 : 056117. doi: 10.1103/PhysRevE.80.056117 |
| [12] | DE MEO P, FERRARA E, FIUMARA G, et al. Generalized Louvain method for community detection in large networks[EB/OL].[2016-03-10]. https://arxiv.org/pdf/1108.1502v2.pdf. |
| [13] | GACH O, HAO J K. Improving the louvain algorithm for community detection with modularity maximization[C]//Proceedings of the 11th International Conference on Artificial Evolution, LNCS 8752. Berlin: Springer, 2013:145-156. |
| [14] | BHOWMICK S, SRINIVASAN S. A template for parallelizing the louvain method for modularity maximization[M]//MUKHERJEE A, CHOUDHURY M, PERUANI F, et al. Dynamics on and of Complex Networks. Berlin: Springer, 2013, 2:111-124. |
| [15] | 刘瑶, 康晓慧, 高红, 等. 基于节点亲密度和度的社会网络社团发现方法[J]. 计算机研究与发展, 2015, 52 (10) : 2363-2372. ( LIU Y, KANG X H, GAO H, et al. A community detecting method based on the node intimacy and degree in social network[J]. Journal of Computer Research and Development, 2015, 52 (10) : 2363-2372. ) |
| [16] | FORTUNATO S, BARTHÉLEMY M. Resolution limit in community detection[J]. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104 (1) : 36-41. doi: 10.1073/pnas.0605965104 |
| [17] | KLIMT B, YANG Y. Introducing the Enron corpus[EB/OL].[2016-03-10]. https://bklimt.com/papers/2004_klimt_ceas.pdf. |
| [18] | YANG J, LESKOVEC J. Defining and evaluating network communities based on ground-truth[J]. Knowledge & Information Systems, 2012, 42 (1) : 745-754. |
| [19] | 王莉, 程学旗. 在线社会网络的动态社区发现及演化[J]. 计算机学报, 2015, 38 (2) : 219-237. ( WANG L, CHENG X Q. Dynamic community in online social network[J]. Chinese Journal of Computers, 2015, 38 (2) : 219-237. ) |




