2. 国网河北省电力公司 信息通信分公司, 石家庄 050021
2. Information and Communication Branch, State Grid Hebei Electric Power Company, Shijiazhuang Hebei 050021, China
近年来, 伴随多媒体服务的发展, 蜂窝网络对数据速率和频谱效率的需求越来越高, 终端直通通信 (Device-to-Device, D2D) 能够复用蜂窝资源来提高频谱的资源利用率, 因而成为研究的热点。D2D通信技术是指邻近的终端可以在近距离的范围内通过直通通信的方式进行数据传输, 而不需要经过基站的转发。在长期演进 (Long Term Evolution, LTE) 中引入D2D通信, 可以减轻基站负担, 减小通信时延。在蜂窝网络中的D2D通信, D2D用户可以在基站的控制下与蜂窝用户共享资源[1], 然而, 这将不可避免地带来蜂窝与D2D用户之间的同频干扰, 因此资源管理和功率控制成为解决问题的关键。
目前, 对D2D通信技术已经有大量的研究。文献提出一个蜂窝用户与一个D2D共享资源的策略, 蜂窝用户之间的资源是相互正交的; 文献分析了多个D2D用户与多个蜂窝用户共享资源的情形, 由于不同D2D用户分配了不同的信道, 限制了频谱效率的进一步提升; 文献提出多个D2D用户可以共享蜂窝资源的分配策略; 文献提出模糊聚类的D2D资源分配算法, 依据D2D用户间的干扰来划分用户簇, 再为D2D簇分配资源。然而, 上述研究都以最优化系统的容量为目标, 在多D2D用户共享蜂窝资源时, D2D用户间的公平性往往得不到保障。
针对上述问题, 在多D2D与蜂窝用户共享资源的情形下, 本文提出了在保障蜂窝用户速率的前提下, 以最大化最小D2D用户容量为目标的功率分配算法。首先, 将关于目标函数的非凸优化问题转化为一个凸函数的差 (Difference of Convex functions, DC) 规划问题, 进一步转化为凸优化问题, 再通过迭代更新的最小容量约束条件使算法快速收敛。仿真结果表明, 本文算法在保证蜂窝用户速率的约束条件下实现了快速收敛, 最大限度地提升了D2D用户间的公平性。
1 系统模型本文考虑单小区场景中多对D2D用户 (D2D User Equipment, DUE) 共享多个蜂窝上行资源进行通信的场景。假设小区包含M对D2D用户和N个蜂窝用户 (Cellular User Equipment, CUE), 为蜂窝用户分配相互正交的信道资源。一般来讲, 应当避免蜂窝用户遭受严重的干扰, 以保证蜂窝用户的正常通信。用pcn和pmn分别表示CUE用户c和DUE用户m在子信道n的功率, Hcn和
| $ \gamma _c^n = \frac{{p_c^nH_c^n}}{{\sum\limits_{m \in M} {p_m^n\tilde H_{m, c}^n + \sigma _0^2} }} $ | (1) |
其中:σ02是噪声功率。与之类似, 用
| $ \gamma _m^n = \frac{{p_m^nH_m^n}}{{\sum\limits_{m' \in M\backslash \{ m\} } {p_{m'}^n\tilde H_{m', m}^n + p_c^n\tilde H_{c, m}^n + \sigma _0^2} }} $ | (2) |
其中:A\B={x|x∈A, x∉B}。用户m的速率为:
| $ {R_m} = \sum\limits_{i = 1}^N {{\rm{lb}}(1 + \gamma _m^n)} $ | (3) |
本文的目标是在保证CUE需求的基础上, 最大化DUE最小传输速率, 问题建模如下:
| $ \begin{array}{l} \;\;\;\;\;\mathop {\max }\limits_\mathit{\boldsymbol{ P}} \mathop {\min }\limits_{m \in M} \;{R_m}(\mathit{\boldsymbol{ P}})\\ {\rm{s}}.{\rm{t}}.\;\;\;\;{C_1}:\;{R_c}(\mathit{\boldsymbol{ P}}) \ge {R_{c,\min }}{\kern 1pt} ;\quad \forall c \in N\\ \,\quad \quad {C_2}\;:\;\sum {p_m^n} \le {p_{d,\max }};\quad \forall m \in M\\ \quad \quad \;{C_3}\;:\;p_c^n \le {p_{c,\max }};\quad \forall c \in N \end{array} $ | (4) |
其中:C1表示CUE的速率要求;C2和C3分别表示DUE和CUE的功率约束;P表示功率向量。问题 (4) 是一个非凸优化问题, 直接求解很难得到全局最优解。
2 功率优化分析多DUE复用多个信道资源的情形, 问题 (4) 的目标函数可以变形为如下DC方程。设共享信道所有用户的集合为Un, 不失一般性地, 用户m的数据速率可表达为:
| $ {R_m}(\mathit{\boldsymbol{P}}) = {f_m}(\mathit{\boldsymbol{P}}) - {g_m}(\mathit{\boldsymbol{P}}) $ | (5) |
其中:
| $ {f_m}(\mathit{\boldsymbol{P}}) = \sum\limits_{n = 1}^N {{\rm{lb}}(p_m^nH_m^n + \sum\limits_{m' \in {U_n}\backslash \{ m\} } {p_{m'}^n\tilde H_{m',m}^n + \sigma _0^2} )} $ | (6) |
| $ {g_m}(\mathit{\boldsymbol{P}}) = \sum\limits_{i = 1}^N {{\rm{lb}}(\sum\limits_{m' \in {U_n}\backslash \{ m\} } {p_{m'}^n\tilde H_{m',m}^n + \sigma _0^2} )} $ | (7) |
将式 (5) 进一步变形为:
| $ {R_m}(\mathit{\boldsymbol{P}}) = {f_m}(\mathit{\boldsymbol{P}}) + \sum\limits_{j \in {U_n}\backslash \{ m\} } {{g_j}(\mathit{\boldsymbol{P}})} - \sum\limits_{j \in {U_n}} {{g_j}(\mathit{\boldsymbol{P}})} $ | (8) |
令
| $ {F_m}(\mathit{\boldsymbol{P}}) = {f_m}(\mathit{\boldsymbol{P}}) + \sum\limits_{j \in {U_n}\backslash \{ m\} } {{g_j}(\mathit{\boldsymbol{P}})} $ | (9) |
| $ G(\mathit{\boldsymbol{P}}) = \sum\limits_{j \in {U_n}} {{g_j}(\mathit{\boldsymbol{P}})} $ | (10) |
则式 (5) 可以改写为:
| $ {R_m}(\mathit{\boldsymbol{P}}) = {F_m}(\mathit{\boldsymbol{P}}) - G(\mathit{\boldsymbol{P}}) $ | (11) |
于是上述问题 (4) 变为:
| $ \begin{array}{l} \;\;\;\;\;\mathop {\max }\limits_\mathit{\boldsymbol{P}} \;F(\mathit{\boldsymbol{P}}) - G(\mathit{\boldsymbol{P}})\quad \\ {\rm{s}}.{\rm{t}}.\;\;\;\;{C_1} \sim {C_3}\rm{in}(4) \end{array} $ | (12) |
其中:
| $ F(\mathit{\boldsymbol{P}}) = \mathop {\min }\limits_{m \in {U_n}} {F_m}(\mathit{\boldsymbol{P}}) $ | (13) |
依据文献, G(P) 可近似为:
| $ G(\mathit{\boldsymbol{P}}) \approx G(\mathit{\boldsymbol{P}}') + \left\langle {\nabla G(\mathit{\boldsymbol{P}}'),\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{P}}'} \right\rangle $ | (14) |
于是有:
| $ F(\mathit{\boldsymbol{P}}) - G(\mathit{\boldsymbol{P}}) \approx F(\mathit{\boldsymbol{P}}) - G(\mathit{\boldsymbol{P}}') - \left\langle {\nabla G(\mathit{\boldsymbol{P}}'),\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{P}}'} \right\rangle $ | (15) |
方程右边是关于P的凸函数, 上述问题可变为一个凸优化问题, 如 (16) 所示, 通过迭代可以找到最优解。
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\mathop {\max }\limits_{\mathit{\boldsymbol{P}},\eta } \quad \eta \\ \,\,\,{\rm{s}}.{\rm{t}}.\;\;\;\;{C_1} \sim {C_3}\;{\rm{in}}\;(4)\\ \quad \;\,\,\,{F_m}(\mathit{\boldsymbol{P}}) - G({\mathit{\boldsymbol{P}}^{(\lambda )}}) - \langle \nabla G({\mathit{\boldsymbol{P}}^{(\lambda )}}),\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{P}}^{(\lambda )}}\rangle \, \ge \eta ;\\ \;\;\;\;\;\;\;\;\;\;\forall m \in M \end{array} $ | (16) |
式 (16) 可以通过CVX (Convex Optimization) 工具箱来求解。初始化P(0), 每个用户功率为最大发送功率, 由于文献算法没有考虑主用户 (蜂窝用户) 的约束条件, 会导致算法收敛慢。对分法可以“跳跃”式找到方程的一个合适的解, 具有收敛快的特点。为了使算法快速收敛, 本文对目标方程增加约束条件 (17), 通过对分算法找到合适的约束值进一步优化用户的发送功率, 然后通过迭代求解方程 (16) 的最优解。
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathop {\max }\limits_\mathit{\boldsymbol{P}} \;\{ F(\mathit{\boldsymbol{P}}) - G({\mathit{\boldsymbol{P}}^{(\lambda )}}) - \langle \nabla G({\mathit{\boldsymbol{P}}^{(\lambda )}}),\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{P}}^{(\lambda )}}\rangle \} \\ \;\;{\rm{s}}.{\rm{t}}.\;\,\;\;{C_1} \sim {C_3}\;{\rm{in}}\;(4)\\ \quad \quad F(\mathit{\boldsymbol{P}}) - G({\mathit{\boldsymbol{P}}^{(\lambda )}}) - \langle \nabla G({\mathit{\boldsymbol{P}}^{(\lambda )}}),\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{P}}^{(\lambda )}}\rangle \ge \beta _m^{(\lambda )};\\ \;\;\;\;\;\;\;\;\;\;\;\forall m \in M \end{array} $ | (17) |
其中βm(λ)表示设置的瓶颈速率。
设多次迭代后的最优功率为Popt, 则有
| $ {R_1}({\mathit{\boldsymbol{P}}_{{\rm{opt}}}}) = {R_2}({\mathit{\boldsymbol{P}}_{{\rm{opt}}}}) = ... = {R_m}({\mathit{\boldsymbol{P}}_{{\rm{opt}}}}) $ | (18) |
设每次求得方程最优解为P*,具体算法流程如下:
1) 将λ、κ、t的初始值置为0, 将P(0)代入方程 (16) 中求解, P(1)=P*。
2) 判断t是否达到门限值, 如果达到门限值,则转到4);否则将最优值P(1)分别代入下列各式中:
| $ \begin{array}{l} r_{\min }^* = \mathop {\min }\limits_{i = 1, 2, ..., m} {R_i}({\mathit{\boldsymbol{P}}^{(1)}})\\ r_m^{(\kappa )} = \mathop {\max }\limits_{i = 1, 2, ..., m} {R_i}({\mathit{\boldsymbol{P}}^{(1)}}) \end{array} $ |
3) 求凸优化问题 (17) 的解P*,如果无解, κ=κ+1, βm(κ)=(βm(κ-1)+rmin*)/2,迭代直至求得解P*;t=t+1, P(t)=P*, 返回2)。
4) 用优化后的功率值P(t)求解方程 (16), λ=λ+1, P(λ)=P*, 计算
以3对DUE为例, 分别考察DUE在复用一个和两个蜂窝信道资源的情形, 采用文献的信道数据, 如式 (19) 和 (20) 所示。其中Ha, b表示用户a到用户b信道增益, 每个CUE占用一个信道, 对应第一行的信道增益, 其余行依次对应DUE1、DUE2和DUE3的信道增益。CUE最大功率为200 mW, 速率约束为3 bps/Hz, DUE最大功率为100 mW, ε取10-10。
| $ {\mathit{\boldsymbol{H}}_1} = \left[ {\begin{array}{*{20}{c}} {0.4310} & {0.0002} & {0.2605} & {0.0039}\\ {0.0002} & {0.3018} & {0.0008} & {0.0054}\\ {0.0129} & {0.0005} & {0.4266} & {0.1007}\\ {0.0011} & {0.0031} & {0.0099} & {0.0634} \end{array}} \right] $ | (19) |
| $ {\mathit{\boldsymbol{H}}_2} = \left[ {\begin{array}{*{20}{c}} {0.1476} & {0.0105} & {0.0018} & {0.0402}\\ {0.0034} & {0.1784} & {0.0013} & {0.2472}\\ {0.0014} & {0.0017} & {0.3164} & {0.0046}\\ {0.0048} & {0.4526} & {0.0012} & {0.6290} \end{array}} \right] $ | (20) |
将本文算法与功率优化算法[9]进行对比。
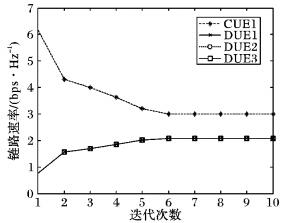
3.2 优化后的用户发送功率和速率DUE用户在共享一个信道H1时, 应用上述迭代算法解问题 (4), 初始化功率为用户功率的最大值, 仿真结果如图 1所示。由图 1可知, 本文算法在6次迭代后蜂窝用户的速率为3.0 bps/Hz, DUE速率收敛于2.085 4 bps/Hz, 优化后各个用户 (CUE1、DUE1、DUE2和DUE3) 的功率值分别为5.779 8 mW, 3.447 6 mW, 18.998 6 mW, 99.998 5 mW。
|
图 1 共享信道H1时优化的用户速率 Figure 1 Optimized data rate of each link when DUE sharing channel H1 |
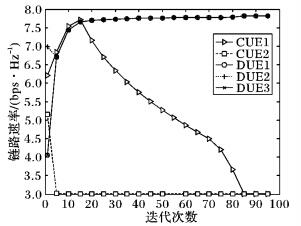
DUE用户在共享两个信道 (H1和H2) 时, 应用上述迭代算法解问题 (4), 初始化DUE在各个信道功率相等, 且DUE功率之和为用户功率的最大值, 其中DUE在共享两个信道时的用户速率仿真结果如图 2所示。可以得出, 在85次迭代后蜂窝用户的速率为3.0 bps/Hz, DUE速率收敛于7.813 9 bps/Hz, 在信道H1上各个用户 (CUE1、DUE1、DUE2和DUE3) 优化后的功率值分别为1.289 2 mW, 99.395 2 mW, 0.944 2 mW, 42.928 2 mW;在信道H2上各个用户 (CUE2、DUE1、DUE2和DUE3) 的优化后的功率值分别为12.683 2 mW, 4.655 0E-10 mW, 36.730 9 mW, 44.981 6 mW。
|
图 2 共享信道H1和H2时优化的用户速率 Figure 2 Optimized data rate of each link when DUE sharing channel H1 and H2 |
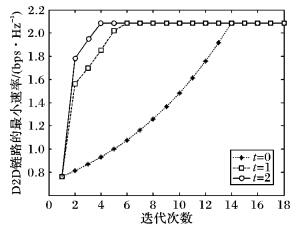
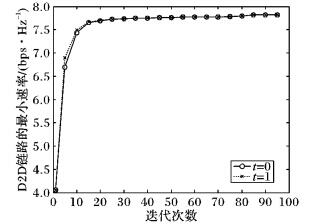
图 3和图 4分别表示D2D用户共享一个信道和两个信道时, 在不同t门限下最小用户速率的收敛情况。t=0表示文献算法, 即不经对分优化, 算法每次迭代的结果和收敛时所需的迭代次数; t>0表示采用对分算法找到的第t个合适的功率值的过程中每次迭代的结果。从图 3~4可以看出经过对分算法的进一步优化, 使用户的功率值更接近收敛值, 加快了算法的收敛。
|
图 3 共享信道H1不同t门限下最小D2D用户速率收敛对比 Figure 3 Comparison of minimal D2D user rate convergence when D2D sharing channel H1 at different thresholds t |
|
图 4 共享信道H1和H2不同t门限下最小D2D用户速率收敛对比 Figure 4 Comparison of minimum D2D user rate convergence when D2D sharing channel H1 and H2 at different thresholds t |
本文引入DC规划对复用蜂窝资源的D2D用户进行功率优化, 最大化D2D用户的最小速率。该算法收敛速度快, 在保证蜂窝用户速率的前提下最大限度实现了D2D用户间的公平性。
| [1] | FODOR G, DAHLMAN E, MILDH G, et al. Design aspects of network assisted device-to-device communications[J]. IEEE Communications Magazine, 2012, 50 (3) : 170-177. doi: 10.1109/MCOM.2012.6163598 |
| [2] | YU C-H, DOPPLER K, RIBEIRO C B, et al. Resource sharing optimization for device-to-device communication underlaying cellular networks[J]. IEEE Transactions on Wireless Communications, 2011, 10 (8) : 2752-2763. doi: 10.1109/TWC.2011.060811.102120 |
| [3] | PEI Y, LIANG Y. Resource allocation for device-to-device communications overlaying two-way cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12 (7) : 3611-3621. doi: 10.1109/TWC.2013.061713.121956 |
| [4] | MIN H, LEE J, PARK S, et al. Capacity enhancement using an interference limited area for device-to-device uplink underlaying cellular networks[J]. IEEE Transactions on Wireless Communications, 2011, 10 (12) : 3995-4000. doi: 10.1109/TWC.2011.100611.101684 |
| [5] | WANG J, ZHU D, ZHAO C, et al. Resource sharing of underlaying device-to-device and uplink cellular communications[J]. IEEE Communications Letters, 2013, 17 (6) : 1148-1151. doi: 10.1109/LCOMM.2013.042313.130239 |
| [6] | ZHAO W, WANG S. Resource allocation for device-to-device communication underlaying cellular networks: an alternating optimization method[J]. IEEE Communications Letters, 2015, 19 (8) : 1398-1401. doi: 10.1109/LCOMM.2015.2444403 |
| [7] | 黄俊伟, 刘晓江, 包瑜, 等. 基于模糊聚类的D2D通信二次资源分配算法设计[J]. 北京联合大学学报 (自然科学版), 2014, 28 (4) : 18-23-29. ( HUANG J W, LIU X J, BAO Y, et al. Design of secondary resource allocation scheme for D2D based on fuzzy cluster[J]. Journal of Beijing Union University (Natural Sciences), 2014, 28 (4) : 18-23-29. ) |
| [8] | HOANG T D, LE L B, LE-NGOC T. Joint subchannel and power allocation for D2D communications in cellular networks[C]//Proceedings of the 2014 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: IEEE, 2014: 1338-1343. |
| [9] | KHA H H, TUAN H D, NGUYEN H H. Fast global optimal power allocation in wireless networks by local DC programming[J]. IEEE Transactions on Wireless Communications, 2012, 11 (2) : 510-515. doi: 10.1109/TWC.2011.120911.110139 |
| [10] | QIAN L, ZHANG Y, HUANG J. MAPEL: achieving global optimality for a non-convex wireless power control problem[J]. IEEE Transactions on Wireless Communications, 2009, 8 (3) : 1553-1563. doi: 10.1109/TWC.2009.080649 |
| [11] | LI Y, SHENG M, WANG X, et al. Max-min energy-efficient power allocation in interference-limited wireless networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64 (9) : 4321-4326. doi: 10.1109/TVT.2014.2361920 |
| [12] | GRANT M, BOYD S, YE Y. CVX users' guide[EB/OL].[2013-09-01]. http://cvxr.com/cvx/cvx_usrguide.pdf. |




