当前, 我们已经跨入到了大数据的时代, 各个行业领域产生的数据正爆炸式地持续增长, 与之伴随的是越来越多的数据成为了社会正常运行不可或缺的部分。为应对由数据量的快速增长而带来的数据存储可靠性问题, 不断提高单个存储节点的稳定性当然是一种理论可行的方法;但更加有效的做法是使用多个存储节点共同构建一个存储系统, 这样做除了能充分利用既有设备、增加存储容量、提高数据并行访问效率外, 结合一定的容错策略后还能有效增强存储系统的整体可靠性。在这种情况下, 通常使用存储节点的数量来表示存储系统的规模。目前节点数目超过100的大规模存储系统已经日益普遍, 而谷歌等公司甚至已经拥有了多个节点数目超过3 000的PB级存储系统[1]。与过去相比, 尽管当前单个存储节点的可靠性已经很高, 但是在拥有众多节点的大规模存储系统中, 一个时间段内多个节点失效的概率依然很高。据卡内基梅隆大学的统计数据显示, 节点数超过300的大规模存储系统中存储节点每年的失效替换率约为5.1%[2]。当然, 这还是存储系统在正常使用状况下的节点失效概率, 如果再将洪水、泥石流、地震等自然灾害和黑客攻击等人为因素考虑在内的话, 存储系统的容错及可靠性增强就更是一个值得关注的问题。
副本技术是目前在存储系统可靠性增强领域中最为成熟的容错技术。采用副本技术的容错方案将多个相同的数据副本存储到系统的不同节点上, 由于每个节点的副本完全相同, 通常可不严格区分校验数据 (冗余数据) 和原始数据, 当有节点失效时, 由任意一个未失效节点中的副本都能恢复出丢失数据。使用副本技术的容错方法简单直观、易于实现及动态扩展, 但是存储效率过低却是其巨大的缺陷。假设使用副本技术构造一个t容错的存储系统, 则需要将原始数据复制成t+1份副本分别存放到不同的节点上, 即存储效率仅为1/(t+1)。显然, 这种极低的存储空间有效利用率是大规模存储系统难以接受的。因为存储系统作为一个整体, 不能仅仅考虑某一项性能参数, 而应根据应用环境兼顾大多重要性能指标。纠删码可以在一定程度上平衡存储系统中的多种主要性能, 是一种日益受到重视的存储系统容错方法。目前, 用于存储系统容错的纠删码主要包括了RS类纠删码 (Reed-Solomon Erasure Codes)、LDPC (Low-Density Parity-Check Codes) 类纠删码,以及阵列纠删码。RS类纠删码是目前唯一一类容错能力不受限制且具备MDS (Maximum Distance Separable) 性质的纠删码, 但其编译码等运算均在多元有限域上进行, 计算复杂度非常高, 特别是多元域上的乘法和求逆。因此, 以RS类纠删码为核心构建存储系统的容错方法需要解决的主要问题不是优化编码, 而是如何大幅提高有限域的计算效率。当然, 目前也有一些研究者针对这一问题进行了卓有成效的工作, 其中最具代表性的工作为Plank等[3]提出的RS码有限域降阶运算方案, 以及有限域运算库GF-Complete[4]。尽管如此, 目前RS码的运算效率仍然很难满足存储系统整体运行性能的需要, 特别是大规模存储系统。LDPC码是源于通信领域的一类纠删码, 其编码和译码过程完全基于异或运算, 与RS码相比, 其纠删能力不受限且运算效率还要高出几个数量级。但是, LDPC码的码字结构不规则和成功译码的概率性却增加了根据应用环境需求设计出与之适应编码的难度。目前基于LDPC码的容错方法在实际存储系统中的应用很少, 已有方法多是以理论研究或实验为主[5]。
阵列纠删码 (通常简称为阵列码) 是编译码运算均使用二元域上异或运算的一类纠删码, 运算效率很高, 具有的二维编码结构可完全对应当前多节点存储系统的数据布局结构, 因此很适合在存储系统中使用。但阵列码在商用存储系统中的使用却非常少, 究其原因可以归纳为如下。一是当前阵列码容错能力普遍偏低, 具备MDS性质的阵列码的最大容错能力通常为2和3[6-9]; 即使是非MDS的阵列码, 在付出了不少的其他性能代价后, 最大容错能力也大多没有超过20[10-13]。此外, 当前大多阵列码在构造时还对存储阵列尺寸有较强的限制条件, 最典型的是素数限制, 即要求存储系统的条带或条带尺寸为一个素数或者和素数严格地保持某种线性关系, EVENODD码[6]、X码[7]、Star码[8]和扩展X码[9]等阵列码在构造时都存在素数限制。其他一些阵列码在构造时的没有这么强的限制条件[10-11], 但却付出了很大的其他性能代价而降低了实用性。比如容错能力达12以上的Weaver码[10], 该码在构造时就无需满足素数限制, 但其存储效率始终低于50%, 且还会随着容错能力的提升而迅速下降。文献提出的阵列码构造方法可以构造出容错能力在理论上没有限制的阵列码, 构造时也无需满足很强的限制条件, 但具体构造步骤却没有明确指出。
针对阵列码存在的这些问题, 本文提出了一类新的阵列纠删码, 该码基于不同斜率的码链构造, 能根据应用环境需求预先设置容错数量, 且容错能力在理论上不受限制。虽然不具备MDS性质, 但该阵列码的存储效率能在不影响容错能力等重要性能的前提下, 随着条块尺寸的增加而不断提高。此外, 该码在构造时也无需满足素数限制这样的强约束条件, 已基本具备在存储系统中使用的条件。
1 基本概念和定义在存储编码领域的常用基本概念, 如数据、校验、冗余、元素、条带、条块、水平阵列码、垂直阵列码、编码、译码、数据重构等, 本文将继续沿用这些概念的定义而不再赘述[10-13]。下面给出的一些符号和概念的定义则是为了配合说明本文方法而提出的。
码链 阵列码是一类线性码, 因此在阵列码中, 任意一个校验元素均由t个数据元素的异或相加得到, 换句话说, 一个校验元素与生成它的所有数据元素的异或和为0。而上述元素像一个链条一样分布于存储阵列中, 为叙述方便而简称为码链, 也可称为编码链或校验链。而部署码链则是将码链上所有的数据元素进行异或求和, 得到对应校验元素并存储于相应位置的过程。
斜率 将存储系统的数据阵列部分 (假设尺寸为m×n, 其中m和n均为大于1的正整数) 看作一个二维坐标系, 以向右的水平轴作为坐标系的正向X轴, 以向下的垂直轴作为坐标系的正向Y轴, 则所有数据阵列中的元素成为了该坐标系上拥有固定坐标的一个点, 假设一条码链上所有存在于数据阵列部分的元素坐标为 (x1, y1), (x2, y2), …, (xt, yt), 若这些元素的坐标满足条件 (1) 则称该码链存在斜率, 且将斜率定义为s=((y2-y1)%n)/(x2-x1)。
| $ ({y_2}-{y_1})\% n = ({y_3}-{y_2})\% n = \cdots = ({y_t}-{y_{t - 1}})\% n $ | (1) |
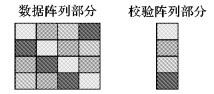
图 1展示了如何部署一条斜率为1的码链。其中, 所有背景色相同的元素异或和为0, 共同构成一条完整码链。
|
图 1 斜率为1的码链 Figure 1 Coding chain with slope 1 |
El(i, j):该符号用于标识存储阵列中第i行第j列的元素, 当有多个元素需要表示时, 可以使用符号“:”表示出一个范围区间, 如El(i, 2:5) 表示存储阵列第i行上的第2到5个元素集合, El(:, j) 则用于表示阵列中第j列的所有元素。
Dji:该符号表示存储阵列的列间距离, 定义Dji=(j-i-1)%n+1, 其中n为条带尺寸, i和j为不大于n的正整数。需要说明的是, 在计算失效列i和j之间距离时, 两个失效列之间若还存在一个及以上的失效列, 则失效列i和j之间不存在距离, 记作Dji=0。将一个存储阵列中f个失效列记作1, 2, …, f, 则失效列 (i-2)%f+1称为失效列i的左邻失效列, 失效列i%f+1称为失效列i的右邻失效列。
2 基于多斜率码链的阵列码垂直阵列码的数据布局结构中, 同一条块中既存储有数据元素又存储有冗余元素, 具有很好的负载平衡性, 但节点间数据的相互依赖性很强, 不便于扩展, 因此本文的新方法采用了典型的水平阵列布局。关于阵列码的构造方法有很多, 常见的包括图论构造法、RS纠删码映射法、代数模型构造方法和几何构造法等。这几种阵列纠删码的构造方法各有优点, 其中使用几何形式的构造方法具有最高的计算效率且更加易于计算机软硬件实现。而本文采用的基于不同斜率码链来组织数据元素和校验元素间关系的方法就是最典型的一种几何构造法。
2.1 编码及数据重构方法如前所述, 为了减少数据及冗余元素间的相互依赖性, 文章采用了典型的水平式阵列结构布局。假设存储系统节点的容错数量为f, 阵列的行数为m, 数据阵列部分的列数为n, 冗余阵列部分的列数为r, 显然f、m、r为正整数, 且m≥2。整个存储阵列的尺寸为m×(n+r)。若无特别说明, 下文在叙述过程中的符号f、m、n、r具有和本段描述相同的含义。
在构造一个f容错的水平阵列码时, 可在数据阵列部分部署斜率从1开始, 并从正负双向渐进扩大的码链f条, 显然所有码链部署完成后将产生冗余元素f·n个, 然后将这些冗余元素按照列优先原则顺序放置于各校验节点上。使用符号d(i, j) 来表示数据阵列部分中第i行第j列所对应的元素, 而直接使用c(t) 表示校验阵列部分的第t个元素, 则存储阵列各元素的标识如图 2所示。其中:i、j、t为正整数, 且1≤i≤m, 1≤j≤n, 1≤t≤f·n。

|
图 2 存储阵列的元素标识 Figure 2 ID of storage array |
在上述数据元素和冗余元素的标识体系下, 任意一个校验元素均可使用式 (2) 计算得出:
| $ \begin{array}{l} c(t) = \sum\limits_{i = 1}^m {d(i, {l_c} + i \cdot (2 \cdot ({l_r}\% 2)-1) \cdot } \\ \;\;\;\;\;\;\;\;\;\left\lceil {{l_r}/2} \right\rceil-1)\% n + 1) \end{array} $ | (2) |
其中:运算符“「⌉”表示向上取整;“%”表示取模; lr表示产生当前校验元素使用的是第lr条码链;lc则表示该条码链是第lc次被使用。lr和lc的计算公式如下:
| $ {l_r} = \left[{(t-1)/n} \right] + 1 $ | (3) |
| $ {l_c} = (t-1)\% n + 1 $ | (4) |
例1 对一个最大容错能力为3, 且条块尺寸为3的存储阵列部署码链, 其中该存储阵列的数据阵列部分有7列。
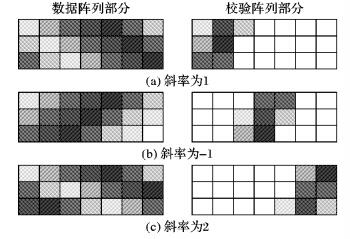
如前所述, 最大容错能力f为3, 数据阵列部分的尺寸为3×7, 则校验元素的数目为21个, 因此校验阵列部分的列数也为7。最大容错能力为3, 因此需要部署斜率为1、-1、2的码链各一条, 具体部署过程如图 3所示, 其中背景色相同的元素异或和为0。
|
图 3 斜率为1、-1、2的码链部署 Figure 3 Deployment of coding chains with slopes 1, -1 and 2 |
用本文方法可以很容易地根据应用环境需求构造出任意容错能力的阵列码。而接下来将简要介绍当有节点失效后如何进行恢复重构。需要说明的是, 本文仅考虑节点错误的情况, 即整个存储节点失效而导致该节点上所有数据元素的丢失, 这也对应存储阵列中整列的数据失效。失效节点上数据恢复的基本思想可以归结为一句话, 即寻找只存在唯一一个失效元素的码链, 显然该码链上的失效元素可由其他有效元素计算恢复。不断重复这一过程, 直到所有失效元素被恢复。
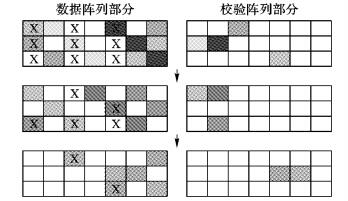
例2 假设在例1所示的存储系统中节点1、3、5失效, 即在将失效节点替换更新后, 存储阵列中数据阵列部分的1、3、5列上的元素数值变得未知, 整个数据恢复过程如图 4所示。其中有“X”标识的元素表示数值未知的失效元素, 而具有相同背景色的元素为仅有一个失效元素的码链, 将该码链上其他元素进行异或相加可恢复失效元素。
|
图 4 失效数据的成功恢复过程 Figure 4 Successful recovery process of invalid data |
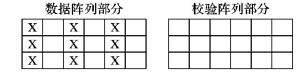
继续扩展例2, 假设数据阵列部分的尺寸为, 仍然是1、3、5列上的元素失效。然而, 如图 5所示, 此时却无法找出任何一条仅包含一个失效元素的码链。在此情况下, 该存储系统中所有的数据丢失。
|
图 5 失败的数据恢复 Figure 5 Failed data recovery |
从例2可以得出如下结论, 如果需要使得条块尺寸为3的存储阵列容错能力达到3, 除了需要部署3条斜率不同的码链外, 数据阵列部分的列数至少不能小于7, 否则将无法保证容错能力。将这一结论进一步扩展, 即仅仅使用不同斜率的f条码链来构造阵列码不能保证容错能力一定是f, 容错数量和阵列尺寸还需要满足某种条件。在此, 首先给出容错能力f、条块尺寸m和数据阵列部分列数n应满足的条件:n≥m·f-f+1。下面将证明在满足该约束条件的情况下, 容错能力就可以得到保证。
对于水平布局的阵列码, 节点级错误的发生情况可以分为如下三种:一是全部失效节点在校验阵列部分, 二是校验阵列部分和数据阵列部分均有失效节点, 三是失效节点全部在数据阵列部分。当所有失效节点都发生于校验阵列部分时, 仅仅需要在替换失效节点后重新做一次编码操作即可, 这是数据重构最简单的情况。当数据阵列部分和校验阵列部分都有失效节点出现时, 也相对容易处理。在f容错的阵列码中, 每个数据元素均有f条码链通过, 因此一个数据元素与f个校验元素相关。根据约束条件可知, n>m, 所以两个与同一数据元素相关的校验元素一定不会出现在同一列。由此, 所有数据阵列部分的失效元素可以被全部恢复, 之后再根据编码方法就可以将校验阵列部分的全部失效元素恢复。而对于f个失效节点全部存在于数据阵列部分的情况, 下面将采用数学归纳法进行证明。
首先, 不妨将数据阵列部分f个失效列记作E1, E2, …, Ef, 其中di记为错误列Ei与其右邻失效列之间的距离, 不妨假设max (d1, d2, …, df)=df, 其中i=1, 2, …, f。因此, 由鸽笼原理可知, df≥m成立。当f=1时, 即仅有一个失效列时, 将该列记作E1。由码链部署方法可知, 每一个数据元素均有一条码链通过, 显然该列上的所有失效元素可以成功恢复。假设当f=k时所有失效元素可以被成功恢复, 其中k为正整数。下面讨论f=k+1的情况。由前提条件可知, max (d1, d2, …, dk)=dk≥m。因此, 若不等式d1≥「m/2⌉成立, 则显然第一个失效列E1上的所有元素均可由斜率为1或-1的码链恢复。同理, 若dk≥「m/2⌉成立, 则最后一个失效列Ek+1上的所有元素均可由斜率为1或-1的码链恢复。至此, 上述两种情况均可化为f=k的情况, 而根据前述假设可知, 所有失效数据能得到恢复。而当d1 < 「m/2⌉且dk < 「m/2⌉时, 显然所有失效列上的第一个失效元素可以被斜率为±1, ±2, …, ±k, k+1的码链恢复。而所有失效列上第一行的失效元素被成功恢复后, 只需不断重复上述相同的步骤, 剩余失效元素可被有效恢复。
因此, 不等式n≥m·f-f+1即是构造阵列码时需要满足的约束条件, 不难看出, 与前文所述的素数约束相比, 本文方法的约束条件非常容易满足, 也有根据实用环境需求动态扩展的空间, 与大多已有阵列码相比, 本文方法的限制条件强度已经有了很大幅度的降低。
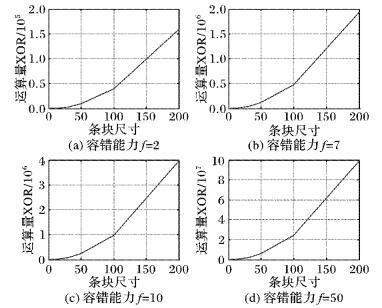
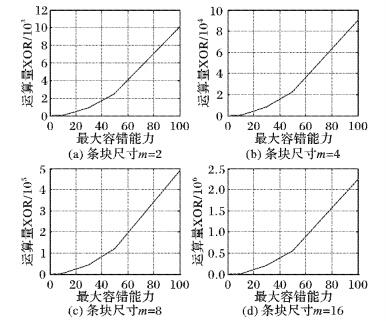
3 实验与分析 3.1 运算工作量由于大多阵列码的码字结构不规则而很难用一个确切的公式来表达编码或数据重构的总体工作量, 因此, 通常使用生成单个校验位所需要经过异或运算的次数来衡量其编码的复杂度, 采用恢复单个丢失数据位需要经过的异或运算的次数来衡量其数据恢复的复杂度。由前文可知, 每条码链的长度均为m+1, 所以生成单个校验位或者恢复单个失效元素所需的计算工作量均为m-1。然而, 条带尺寸会随着条块尺寸m或容错能力f的扩大而增加, 这就意味着校验位的数量也将增加, 即总体运算量加大。因此, 存储阵列的条块尺寸以及容错能力的变化对编码和数据恢复运算量的影响是需要考虑的一个因素。假设条块尺寸200, 容错能力为50的情况下, 以存储1 GB的数据为例, 生成所有校验位或恢复50个节点的失效数据所需要的异或运算次数约为4.2×109, 这些运算量用一台主频为3.2 GHz的普通个人电脑大概也只需要16 s就能完成。图 6显示了条块尺寸对阵列码编码和数据恢复运算量的影响情况, 而图 7则显示了容错能力对编码和数据恢复运算量的影响情况。
|
图 6 条块尺寸对运算量的影响 Figure 6 Influence of strip size on operational burden |
|
图 7 容错能力对运算量的影响 Figure 7 Influence of fault tolerance on operational burden |
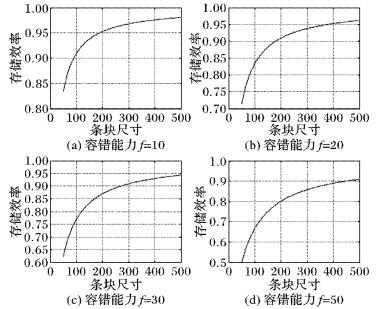
如前所述, 以存储效率为标准, 目前的阵列码可以划分为MDS编码和非MDS编码。MDS编码在存储效率上具有理论上的最优值, 其典型代表包括以EVENODD码[6]、X码[7]、Star码[8]和扩展X码[9]等。但是具有MDS性质的阵列码通常的容错能力仅为2或3, 这显然不能满足现代大规模存储系统的可靠性增强需求。而为了提高阵列码的容错能力, 研究者们则设计出一些不具备MDS性质的阵列码, 其容错能力与具有MDS性质的阵列码相比有较大提升 (通常在10个以上), 即通过降低存储效率 (在不小于复制冗余策略的前提下) 以换取更高的容错能力, 这类编码的典型代表包括Weaver码[10]、Hover码[11]和Grid码[12]等。但大多对于存储效率的牺牲很大, 比如Weaver码在容错能力为10时, 其存储效率还不足20%。而本文提出的编码也是一种典型的非MDS阵列编码, 因此也不具有最优的存储效率, 但可以在保证较高容错能力的前提下, 达到较高的存储效率。如图 8所示, 在具有较高容错能力时, 本文提出的阵列码依然可以达到较高的存储效率。
|
图 8 存储效率的变化 Figure 8 Changes on storage efficiency |
修复代价通常是指重构一个失效的数据元素所需要涉及到读操作的存储节点总数。修复代价是存储系统中一个重要的性能指标, 与数据重构、数据更新、降低读写等均有密切的关系。由前述码链的部署方法可得, 每条码链上均有m+1(m个数据元素和1个校验元素) 个元素, 因此, 重构一个失效数据元素需要涉及的节点数总是m, 且不会随着存储系统规模和容错能力的增加而增大。
更新代价是水平布局阵列码中的一个特有指标, 它是指一个最小的数据位改变时所需要涉及到的校验节点数。数据更新比较频繁时, 更新代价过高会导致校验节点的访问过热而降低存储系统的整体I/O性能。由本文阵列码构造方法可知, 每个数据元素均刚好有f条不同码链通过, 即每个数据元素均有f个不同的校验元素与之相关。换句话说, 当任意一个数据元素改变时, 总是会涉及到f个校验节点, 即更新代价恒为f, 而这也已经达到了f容错阵列码更新代价的理论最优值。
4 结语本文使用不同斜率码链构造出了一类容错能力理论上不受限制的阵列纠删码, 其结构简洁, 有利于计算机软硬件实现。该码涉及的所有计算均使用二进制的异或运算, 具有极高的运算效率; 而构造时也无需满足素数约束等强约束条件, 易于实用且便于扩展。虽然该码不具备MDS性质, 但存储效率可以通过条块尺寸的增加而不断提高。此外, 该码的修复代价和更新代价均为一个常量, 不会随着系统规模或容错能力的提高而增加。
| [1] | SATHIAMOORTHY M, ASTERIS M, PAPAILIOPOULOS D, et al. XORing elephants: novel erasure codes for big data[J]. Proceedings of the VLDB Endowment, 2013, 6 (5) : 325-336. doi: 10.14778/2535573 |
| [2] | SCHROEDER B, GIBSON G A. Disk failures in the real world: what does an MTTF of 1000000 hours mean to you?[C]//FAST 2007: Proceedings of the 5th USENIX Conference on File and Storage Technologies. Berkeley, CA: USENIX Association, 2007:1-16. |
| [3] | PLANK J S, XU L. Optimizing Cauchy Reed-Solomon codes for fault-tolerant network storage applications[C]//NCA 2006: Proceedings of the Fifth IEEE International Symposium on Network Computing and Applications. Washington, DC: IEEE Computer Society, 2006:173-180. |
| [4] | PLANK J S, GREENAN K M, MILLER E L. Screaming fast Galois field arithmetic using Intel SIMD instructions[C]//FAST 2013: Proceedings of the 11th USENIX Conference on File and Storage Technologies. Berkeley, CA: USENIX Association, 2013: 299-306. |
| [5] | JANAKIRAM B, CHANDRA M G, ARAVIND K G, et al. SpreadStore: a LDPC erasure code scheme for distributed storage system[C]//Proceedings of the 2010 International Conference on Data Storage and Data Engineering. Piscataway, NJ: IEEE, 2010: 154-158. |
| [6] | BLAUM M, BRADY J, BRUCK J, et al. EVENODD: an efficient scheme for tolerating double disk failures in RAID architectures[J]. IEEE Transactions on Computers, 1995, 44 (2) : 192-202. doi: 10.1109/12.364531 |
| [7] | XU L, BRUCK J. X-code: MDS array codes with optimal encoding[J]. IEEE Transactions on Information Theory, 1999, 45 (1) : 272-276. doi: 10.1109/18.746809 |
| [8] | HUANG C, XU L. STAR: an efficient coding scheme for correcting triple storage node failures[J]. IEEE Transactions on Computers, 2008, 57 (7) : 889-901. doi: 10.1109/TC.2007.70830 |
| [9] | 孟庆春. 应用于分布式存储系统上的纠删码技术研究[D]. 北京: 中国科学院研究生院, 2007. ( MENG Q C. Research of erasure codes applied in distributed storage system[D]. Beijing: Graduate University of the Chinese Academy of Sciences, 2007. ) |
| [10] | HAFNER J L. WEAVER codes: highly fault tolerant erasure codes for storage systems[C]//FAST 2005: Proceedings of the 4th Conference on USENIX Conference on File and Storage Technologies. Berkeley, CA: USENIX Association, 2005, 4: 211-224. |
| [11] | HAFNER J L. HoVer erasure codes for disk arrays[C]//DSN 2006: Proceedings of the 2006 International Conference on Dependable Systems and Networks. Washington, DC: IEEE Computer Society, 2006: 217-226. |
| [12] | LI M, SHU J, ZHENG W. GRID codes: strip-based erasure codes with high fault tolerance for storage systems[J]. ACM Transactions on Storage, 2009, 4 (4) : Article No. 15. |
| [13] | 陈峥. 一类新的阵列纠删码理论及应用研究[D]. 北京: 中国科学院研究生院, 2009. ( CHEN Z. A class of array erasure codes and their applications[D]. Beijing: Graduate University of the Chinese Academy of Sciences, 2009. ) |
| [14] | 唐聃, 舒红平. 一类多容错的阵列纠删码[J]. 中国科学:信息科学, 2016, 46 (4) : 523-538. ( TANG D, SHU H P. A class of array erasure codes with high fault-tolerance[J]. Science China: Information Sciences, 2016, 46 (4) : 523-538. ) |




