2. 成都工业职业技术学院, 成都 610218
2. Chengdu Vocational and Technical College of Industry, Chengdu Sichuan 610218, China
正常情况下, 配准后的解剖结构图像与参考图像应具有相同的拓扑结构, 不会产生新的组织, 原有的结构不会消失, 形变域也不会出现撕裂、折叠、空洞等不合理的物理结构。微分同胚是一种平滑、连续和可逆的变换, 能够使解剖结构图像变形后的拓扑结构保持不变, 在医学图像配准中是一个重要的应用。
Marsland等[1]把微分同胚变换看作时变速度场, 用测地插值样条基构造变换; Beg等[2]提出在速度场空间利用基于欧拉-拉格朗日方程的变分方法求解大形变的微分同胚变换, 采用梯度下降法更新形变参数; Ashburner等[3]对文献[2]进行改进, 任意时刻的速度场都用初始速度场来表示, 配准的每次迭代都利用初始形变值来计算, 减少了对内存和外存的要求; Ashburner[4]提出非时变速度场的配准方法, 同胚变换构成了复合运算下的李群, 将大形变同胚变换分解为一系列小形变来处理, 使可逆变换相对容易, 并降低计算代价; Janssens等[5]在微分同胚方法中利用累加位移场的可逆性配准对比增强度不同的图像; Arsigny等[6]借助李群理论提出Log-Euclidean框架, 在微分同胚空间里可以对向量场进行分析统计并且能保持变换的可逆性; Vercauteren等[7]基于Demons算法, 提出一种非参数微分同胚的Demons配准算法——DD-NP算法, 利用李群理论在连续域上进行空间变换, 使空间变换具有微分同胚性, 从而形变场具有拓扑保持性; 闫德勤等[8]在保持图像的局部和全局流形拓扑结构的基础上, 提出快速微分同胚变换速度场更新方法。
但是, 上述方法都没有考虑高维微分同胚变换空间中数据的非线性结构, 高维数据包含更多的结构信息, 影响配准结果。针对这个问题, 结合流形学习方法[9], 本文改进DD-NP配准算法, 提出了一种基于自适应切空间的MRI图像配准方法。首先, 构造正定对称的协方差矩阵, 协方差的空间结构是一个高维黎曼流形, 一定条件下形成李群; 其次, 利用样本点邻域的局部切空间来表示李群流形的几何结构的非线性; 接下来, 由于局部切空间的线性化程度越高, 高维数据流形的非线性结构信息就越丰富, 在空间变换中则可以最大限度上保留流形的局部非线性结构,于是用自适应邻域选择的方法形成的线性子空间去逼近局部切空间, 更好地在空间变换中保持图像的拓扑结构, 从而提高图像配准的精度。
1 相关背景 1.1 李群和切空间流形是一个拓扑空间, 微分流形是把m维流形M加上微分结构。李群既是一种微分流形也是一种群。在李群的单位元Id处的切空间构成一个向量空间, 即李代数。为了方便描述, 先作如下规定:
1)GL(m) 表示m×m矩阵构成的李群;
2)gl(m) 表示m×m矩阵构成的李代数 (线性向量空间);
3) log () 表示对数映射;
4) exp () 表示指数映射。
指数和对数映射可由式 (1) 进行转换:
| $ {{\mathit{\boldsymbol{S}}}_{i}}=\exp ({{\mathit{\boldsymbol{s}}}_{i}});{{\mathit{\boldsymbol{s}}}_{i}}=\log ({{\mathit{\boldsymbol{S}}}_{i}}) $ | (1) |
其中:Si∈ GL(m), si∈ gl(m)。指数映射使m维流形局部同胚于m维向量空间, 即李代数零元素的邻域通过指数函数映射到李群的单位元邻域, 指数映射及其逆映射对数映射都是光滑可逆的同胚映射, 如图 1所示。但是在高维流形空间, 影响切空间逼近的邻域大小目前并不清楚[10]。
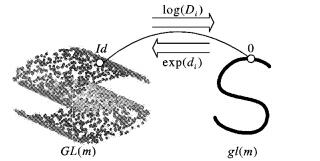
|
图 1 李群和李代数之间的映射关系 Figure 1 Mapping between Lie group and Lie algebra |
正定对称的形式有很多, 比如区域协方差特征描述子[11]和结构张量[12]。正定对称结构是包含了丰富结构信息的黎曼流形,但不具有群结构, 记Sym+(m) 是m×m的正定对称矩阵构成的流形空间。根据文献[13], 附加式 (2) 约束则可以形成李群 (Sym+, ⊙)。
| $ {{\mathit{\boldsymbol{S}}}_{i}}\odot {{\mathit{\boldsymbol{S}}}_{j}}=\exp (\log ({{\mathit{\boldsymbol{S}}}_{i}})+\log ({{\mathit{\boldsymbol{S}}}_{j}})) $ | (2) |
在DD-NP模型中, 配准的空间变换是一个微分同胚群。现给定一个参考图像Ir和一个浮动图像If, 并设有一个样本集{S1,S2,…,Si,…,Sn}
| $ \min \mathit{\boldsymbol{E}}(u)=Sim({{I}_{r}}, {{I}_{f}}\circ \varphi )+Reg(\varphi ) $ | (3) |
其中:Sim(·) 和Reg(·) 分别表示相似性函数和正则化函数。式 (3) 的目的就是寻找一个最优的空间变换φ(Si)=φ(Si, t)。其中:t∈[0,1];φ(Si, t) 是速度流;u是依赖于时间的速度场。φ通过求式 (4) 的常微分方程可得:
| $ \frac{\rm{d}\varphi ({{\mathit{\boldsymbol{S}}}_{i}}, \mathit{t})}{\rm{d}\mathit{t}}=u(\varphi ({{\mathit{\boldsymbol{S}}}_{i}}, t), t);\varphi ({{\mathit{\boldsymbol{S}}}_{i}}, 0)={{\mathit{\boldsymbol{S}}}_{i}} $ | (4) |
对任何邻域点Sij都存在一个u∈gl(m)。当t=1时, φ(Si, 1)=exp (u(si)), 通过指数映射exp (u) 的有限复合得到群变换φ∈GL(m), 根据式 (5) 表达复合的微分同胚变换:
| $ {{S}_{i}}^{j}={{\mathit{\boldsymbol{S}}}_{i}}\circ \varphi ={{\mathit{\boldsymbol{S}}}_{i}}\circ \exp (u) $ | (5) |
在条件exp (u(0))=Id约束下, 李代数零点邻域和李群单位元邻域的同胚对应关系是唯一的, 以保证空间变换的一一映射特性, 配准前后的浮动图像仍保持邻接关系, 使配准后的图像结构保持拓扑性。
3 基于自适应切空间的配准算法 3.1 自适应邻域选择流形上任一点附近的局部线性结构都能被流形在该点处的切空间描述, 切空间是该局部线性化子空间, 线性化程度越高, 包含的流形的非线性结构越多。算法的目的是在李群流形下, 用自适应的邻域选择方法[9]去逼近单位元处的切空间。邻域大小与样本点的曲率密切相关, 流形上曲率是高度变化的, 曲率大的样本点的邻域应该相对比较小, 而流形上曲率小的样本点处的邻域比较大, 这样能更精确地逼近流形的局部几何结构。
假设李群的单位元Id处切空间是TG, 其d维正交基矩阵为
| $ \mathit{\boldsymbol{u}}=\sum\limits_{i=1}^{d}{{{u}^{i}}}{{\tau }_{i}} $ | (6) |
其中:ui是给定坐标下u的分量, 是线性组合系数。
设Eε是单位元Id的邻域, 且Eε由k个最近邻点{ε1, ε2, …, εk}组成, εj∈Sym+(m), j=1, 2, …, k, 邻域点的线性逼近用线性拟合
| $ \sum\limits_{j=1}^{k}{||{{\varepsilon }_{j}}}-(\bar{\varepsilon }+\mathit{\boldsymbol{T}}{{u}^{j}})||=||{{\mathit{\boldsymbol{E}}}_{\varepsilon }}-(\bar{\varepsilon }{{\mathit{\boldsymbol{e}}}^{\rm{T}}}+\mathit{\boldsymbol{TU}})|| $ | (7) |
其中:T∈Rm×d是构成切空间的正交基矩阵;ε是k个最近邻的均值。通过局部主分量分析 (Principal Component Analysis, PCA) 方法, 得到邻域点εj在局部邻域上的投影uj, 令uj=TT(εj-ε), j=1, 2, …, k。
设
| $ \mathit{\boldsymbol{U}}={{\mathit{\boldsymbol{T}}}^{\rm{T}}}({{\mathit{\boldsymbol{E}}}_{\varepsilon }}-\bar{\varepsilon }{{\mathit{\boldsymbol{e}}}^{\rm{T}}}) $ | (8) |
用奇异值分解 (Singular Value Decomposition, SVD) 方法分解式 (8) 中的Eε-εeT部分得到k个奇异值, 按序排列为σ1≥…≥σd≥…≥σk, U可用式 (9) 来表示:
| $ \mathit{\boldsymbol{U}}=\rm{diag}({{\sigma }_{1}}, {{\sigma }_{2}}, \cdots, {{\sigma }_{d}}){{\mathit{\boldsymbol{V}}}^{\rm{T}}} $ | (9) |
其中:VT是Eε-εeT的d个最大奇异值对应的右奇异向量, 则T是左奇异向量构成的正交基矩阵。
从而有
| $ \left\| \mathit{\boldsymbol{U}} \right\|=\sqrt{\sum\limits_{j\le d}{{{({{\sigma }_{j}})}^{2}}}} $ | (10) |
以及
| $ \left\| {{\mathit{\boldsymbol{E}}}_{\varepsilon }}-(\bar{\varepsilon }{{\mathit{\boldsymbol{e}}}^{\rm{T}}}+\mathit{\boldsymbol{T}}\mathit{\Theta }) \right\|=\sqrt{\sum\limits_{j>d}{{{({{\sigma }_{j}})}^{2}}}} $ | (11) |
由式 (10) 和 (11) 得到邻域选择标准式 (12):
| $ r=\sqrt{\sum\limits_{j\ge d}{{{({{\sigma }_{j}})}^{2}}}}/\sqrt{\sum\limits_{j>d}{{{({{\sigma }_{j}})}^{2}}}} $ | (12) |
本文算法步骤如下:
输入:参考图像Ir和浮动图像If。
输出:配准图像。
步骤1 对Ir和If中的像素提取对称正定的图像特征。
步骤2 预先设定一个最小邻域Kmin和用k-邻域法[14]确定一个比较大的初始的单位元邻域集Eεk。
步骤3 用奇异值分解Eε-εeT并计算比值r。
步骤4 设定阈值α∈[0,1], 如果r < α, 则算法结束;否则到下一步。
步骤5 如果r≥α且k>kmin, 则移除距离邻域均值ε最远的点, 让Eεk←Eεk-1, 使邻域尺寸缩小, 然后返回步骤3。
步骤6 利用上面得到的邻域集Eεk扩张邻域尺寸:把初始邻域中没有选中的点回加到步骤5得到的邻域集里, 设定约束条件为
步骤7 计算李群单位元Id处邻域所对应的切空间的正交基矩阵
步骤8 通过最小化式 (3) 中的代价函数得到最优空间变换φ。
4 实验与分析为了验证本文算法的有效性, 在仿真数据和临床数据上对大脑白质和大脑灰质的MRI图像分别进行实验, 并与DD-NP算法对比。实验平台为:3.4 GHz CPU, 8 GB RAM内存, Windows 8操作系统, Matlab 2012b, 采用C++和Matlab混合编程。评价标准采用可视评估和均方根误差 (Root Mean Squared Error, RMSE)。
4.1 构造正定对称的图像特征对选取的每个样本像素构造一个136×136的正定对称的协方差矩阵作为图像特征。先提取136维局部特征fi, 包括128维的SIFT (Scale-Invariant Feature Transform) 描述子、坐标位置 (x, y)、灰度值Ii(x y)、灰度值的一阶梯度、一阶梯度的模和二阶梯度, 如式 (13) 所示:
| $ \begin{align} & {{\mathit{\boldsymbol{f}}}_{i}}=[SIFT, x, y, {{I}_{i}}(x y), |\frac{\partial }{\partial x}{{I}_{i}}(x y)|, |\frac{\partial }{\partial y}{{I}_{i}}(x y)| \\ & \sqrt{ |\frac{\partial }{\partial x}{{I}_{i}}(x y){{|}^{^{2}}}+ |\frac{\partial }{\partial y}{{I}_{i}}(x y){{|}^{^{2}}}} |\frac{{{\partial }^{2}}}{\partial x\partial x}{{I}_{i}}(x y)| \\ & |\frac{{{\partial }^{2}}}{\partial y\partial y}{{I}_{i}}(x y)| {{]}^{\rm{T}}} \\ \end{align} $ | (13) |
然后用fi和fi的转置作外积计算, 得到式 (14) 所示的正定对称的协方差矩阵:
| $ {{\mathit{\boldsymbol{S}}}_{i}}={{\mathit{\boldsymbol{f}}}_{i}}{{\mathit{\boldsymbol{f}}}_{i}}^{\rm{T}} $ | (14) |
为了减少噪声影响和计算代价, 对协方差矩阵形成的高维流形Sym+(m) 作PCA降维处理, 并在实验中发现当维数m=126, 116, 106时, 得到的效果最好。
4.2 仿真数据实验及分析仿真数据来源于Brain Web数据库, 灰度值在0~255, 图像大小为181×217×181。先从数据库中随机抽取两个主体 (subject 18和subject 46), 然后实验分为两组:第一组从两个主体的大脑白质图像中随机选择横断面, 冠状面和矢状面各一张, 一张作为参考图像, 另一张作为浮动图像; 第二组从两个主体的大脑灰质图像中随机选择横断面, 冠状面和矢状面各一张, 一张作为参考图像, 另一张作为浮动图像。两组实验各进行10次, 最后计算每10次实验的平均RMSE。
图 2~3显示了不同情况下本文算法最好的可视化结果和DD-NP算法结果的对比。从可视效果的角度, 本文算法在这几种情况下的可视效果明显优于DD-NP算法。
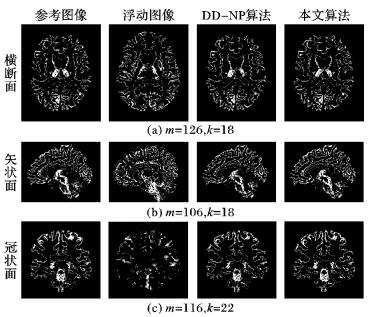
|
图 2 仿真数据在大脑白质图像上的配准结果 Figure 2 Synthetic results on white matter images |
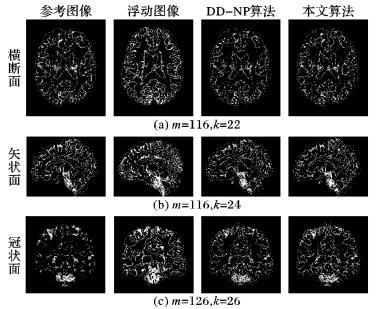
|
图 3 仿真数据在大脑灰质图像上的配准结果 Figure 3 Synthetic results on gray matter images |
表 1~2对比了在大脑白质和灰质中不同维数和邻域对应的配准误差结果,可看出配准的精度不仅和邻域大小有关,也和流形的维数有关。从三个不同断面的图像配准结果可以看到, 尽管本文算法有的情况下实验误差要比DD-NP算法的误差大, 但是在每一个断面都能获得误差小于DD-NP算法的结果。例如在白质图像横断面的配准中, DD-NP的误差为2.26, 本文算法当维数m=126, k=22; m=116, k=18和m=116, k=20这三种情况下, 误差 ((表中加粗数据) 均小于DD-NP,样本点非线性结构的投影方向和流形的曲率密切相关,流形上点切方向的曲率反映了曲率沿着切方向的弯曲程度, 也就是局部线性化的程度。样本点的曲率越大, 线性化程度越低, 所以为了达到高精度的切空间逼近, 那么邻域选取可以较小; 在极小主曲率方向的线性化程度最高, 邻域选取可以较大。从图 2~3可看出, 冠状面样本点的曲率要比横断面和矢状面小, 所以选择较大的邻域可以得到更好的实验效果,但是邻域的选取也会受流形维数的影响。
| 表 1 大脑白质图像上RMSE对比 Table 1 Comparison of RMSE on white matter images |
| 表 2 大脑灰质图像上RMSE对比 Table 2 Comparison of RMSE on gray matter images |
数据采集来自西门子核磁共振仪, 回波时间TE=2.98 ms, 回波链长度ETL=1, 反转时间TI=1100 ms, 重复时间TR=2530 ms, 视野FOV=87.5, 图像大小448×512×192, 20个健康主体大脑图像。随机抽选4个主体的矢状面图像, 然后分为两组:一组用于分割大脑白质, 另一组用于分割大脑灰质。每组选一张作为参考图像, 另一张为浮动图像。
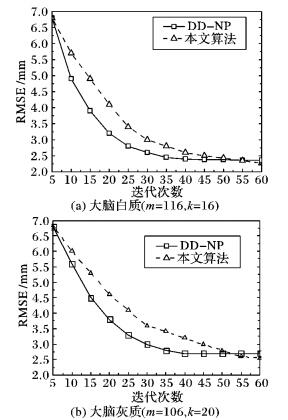
图 4(a)和(b)分别显示了临床数据的大脑白质和灰质配准在两种算法上的对比可视化结果, 本文算法的灰质图像情况下的效果明显优于DD-NP。图 5显示在m=116, k=16时,本文算法与DD-NP算法在大脑白质和大脑灰质图像上的误差与迭代关系。由于需要在高维空间和切空间之间作映射, 本文算法需要更多的迭代次数才能达到收敛。DD-NP算法迭代30次后开始产生收敛, 而本文算法需要60次, 但是第60次迭代以后本文算法的误差小于DD-NP算法。
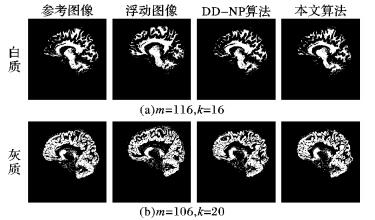
|
图 4 临床数据的配准结果对比 Figure 4 Comparison of clinical data |
|
图 5 临床数据中RMSE的对比 Figure 5 RMSE comparison of clinical data |
传统的微分同胚配准算法没有考虑高维空间数据的非线性结构; 然而, 高维数据流形的非线性结构受局部线性化程度影响。本文利用流形学习方法提出一种基于切空间的配准算法, 通过自适应的邻域选择更精确地逼近流形的线性切空间, 保持流形的非线性结构, 使图像在微分同胚变换中更好地保持拓扑结构。实验显示, 比起传统算法, 本文算法配准精度有明显提高。
进一步的工作将关注以下两点:1) 如何减少由于高维空间中的迭代映射造成的计算代价; 2) 目前在理论上并不清楚多大的邻域和流形维数能获得最优结果, 算法只能通过枚举去搜索, 如果能找到规律, 将大大减少工作量。
| [1] | MARSLAND S, TWINING C J. Constructing diffeomorphic representations for the groupwise analysis of nonrigid registrations of medical images[J]. IEEE Transactions on Medical Imaging, 2004, 23 (8) : 1006-1020. doi: 10.1109/TMI.2004.831228 |
| [2] | BEG M F, MILLER M I, TROUVÉ A, et al. Computing large deformation metric mappings via geodesic flows of diffeomorphisms[J]. International Journal of Computer Vision, 2005, 61 (2) : 139-157. doi: 10.1023/B:VISI.0000043755.93987.aa |
| [3] | ASHBUMER J, FRISTON K J. Diffeomorphic registration using geodesic shooting and Gauss-Newton optimization[J]. Neuroimage, 2011, 55 (3) : 954-967. doi: 10.1016/j.neuroimage.2010.12.049 |
| [4] | ASHBUMER J. A fast diffeomorphic image registration algorithm[J]. Neuroimage, 2007, 38 (1) : 95-113. doi: 10.1016/j.neuroimage.2007.07.007 |
| [5] | JANSSENS G, JACQUES L, DE XIVRY J O, et al. Diffeomorphic registration of images with variable contrast enhancement[J]. Journal of Biomedical Imaging, 2011, 2011 : 3. |
| [6] | ARSIGNY V, COMMOWICK O, PENNEC X, et al. A Log-Euclidean framework for statistics on diffeomorphisms[C]//MICCAI 2006: Proceedings of the 9th International Conference on Medical Image Computing and Computer-Assisted Intervention, LNCS 4190. Berlin: Springer, 2006: 924-931. |
| [7] | VERCAUTEREN T, PENNEC X, PERCHANT A, et al. Diffeomorphic demons: efficient non-parametric image registration[J]. Neuroimage, 2009, 45 (1) : S61-S72. doi: 10.1016/j.neuroimage.2008.10.040 |
| [8] | 闫德勤, 刘彩凤, 刘胜蓝, 等. 大形变微分同胚图像配准快速算法[J]. 自动化学报, 2015, 4 (8) : 1461-1470. ( YAN D Q, LIU C F, LIU S L, et al. A fast image registration algorithm for diffeomorphic image with large deformation[J]. Acta Automatica Sinica, 2015, 4 (8) : 1461-1470. ) |
| [9] | ZHANG Z, WANG J, ZHA H. Adaptive manifold learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34 (2) : 253-265. doi: 10.1109/TPAMI.2011.115 |
| [10] | ARSIGNY V. Processing data in Lie groups: an algebraic approach. application to non-linear registration and diffusion tensor MRI[EB/OL].[2016-03-01]. https://tel.archives-ouvertes.fr/tel-00121162/. |
| [11] | TUZEL O, PORUKI F, MEER P. Region covariance: a fast descriptor for detection and classification[C]//ECCV 2006: Proceedings of the 9th European Conference on Computer Vision, LNCS 3952. Berlin: Springer, 2006: 589-600. |
| [12] | GOH A, LENGLET C, THOMPSON P M, et al. A nonparametric Riemannian framework for processing high angular resolution diffusion images (HARDI)[C]//CVPR 2009: Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2009: 2496-2503. |
| [13] | ARSIGNY V, FILLARD P, PENNEC X, et al. Geometric means in a novel vector space structure on symmetric positive-definite matrices[J]. SIAM Journal on Matrix Analysis and Applications, 2007, 29 (1) : 328-347. doi: 10.1137/050637996 |
| [14] | TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290 (5500) : 2319-2323. doi: 10.1126/science.290.5500.2319 |




