2. 北京邮电大学 电子工程学院, 北京 100876
2. School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
图像修复指的是利用先验信息对图像中信息缺失的区域进行修正, 以达到视觉上合理的效果[1]。图像修复是图像处理领域中一个重要的研究方向, 其研究成果已经得到了广泛的运用, 包括文物保护、文字去除、影视效果制作等方面。目前的图像修复方法主要分为两大类:基于偏微分方程的方法和基于纹理合成的方法。
基于偏微分方程的图像修复算法利用待修复区域边缘的信息估计等值线的方向, 然后将待修复区域周围的信息传播到待修复区中[2-3], 这类方法是基于像素级的操作, 对于大面积的待修复区, 会出现过平滑和模糊的现象。基于纹理合成的图像修复算法以图像块为基本修复单元[4-8], Criminisi等[6]通过寻找最佳匹配图像块, 替换待修复图像块, 该方法能够有效地修复大面积受损区域, 但是往往造成结构上的不连续性。文献[9]在Criminisi的基础上改进了待修复图像块的优先级, 并对待修复图像块进行稀疏表达。Mairal等[10]提出了一种基于非局部稀疏表示的图像修复方法, 将字典学习和稀疏编码合并在统一的框架中。
为了更充分地利用自然图像中的先验信息, 文献[11-12]扩展了图像块的概念, 提出了以相似图像块组作为基本修复单元, 并且分别在图像修复和图像去噪中取得了明显的效果。但是它们都是根据固定数目的相似图像块, 构造尺寸固定的组, 因此不能有效地区分自然图像中的结构区和纹理区。本文在此基础上, 进一步提出了自适应相似组的概念, 并以此作为稀疏表示的基本单元。为了更准确地描述图像块之间的相似性, 本文采用结构相似性指数[13]作为图像块相似性的判别准则。最后, 通过实验对算法进行验证, 表明该算法具有较强的自适应性, 能够有效地进行图像修复。
1 算法描述 1.1 自适应相似组对于待修复图像块Ψk∈R
| $ SSIM(x, y)=\frac{(2{{\mu }_{x}}{{\mu }_{y}}+{{C}_{1}})(2{{\sigma }_{xy}}+{{C}_{2}})}{(\mu _{x}^{2}+\mu _{y}^{2}+{{C}_{1}})(\sigma _{x}^{2}+\sigma _{y}^{2}+{{C}_{2}})} $ | (1) |
其中: μx、μy是亮度均值作为亮度估计;σx、σy是标准方差作为对比度估计。结构相似性指数越大, 表明x和y的相似性越高。
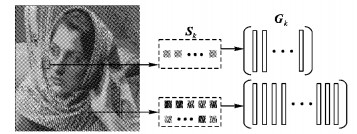
将所有图像块均表示成向量的形式Ψk∈Rβ, 其相似图像块集合Sk可以表示成矩阵的紧凑形式Gk∈Rβ×nk, 则称Gk为图像块Ψk的一个相似组。在自然图像中, 位于纹理区的图像块具有较多的相似图像块, 而位于结构区的图像块则具有较少的相似图像块[9], 因此, 不同的待修复图像块Ψk将对应不同尺寸的相似组Gk, 即所构造的相似组是自适应的。定义Gk=Rk(I) 为从图像I中提取相似组Gk(k=1, 2, …, N) 的操作, 则相似组的构造过程如图 1所示。
|
图 1 自适应相似组的构造 Figure 1 Construction of self-adaptive group |
给定集合Dk={dk, 1, dk, 2, …, dk, nk}, 其元素dk, m (m=1, 2, …, nk) 为与相似组Gk相同尺寸大小的矩阵, 即dk, m∈Rβ×nk, 称集合Dk为字典, 元素dk, m为原子。根据稀疏表示理论, 对任意给定的相似组Gk∈Rβ×nk, 都能用字典Dk中原子的线性组合近似表示, 即:
| $ {{{\mathrm{\hat{G}}}}_{k}}=\sum\limits_{m=1}^{{{n}_{k}}}{{{\mathrm{d}}_{k, m}}}{{\alpha }_{k, m}} $ | (2) |
其中: α k=[αk, 1, αk, 2, …, αk, nk]为稀疏的系数向量, 即只有少数元素不为零。为了论述和表示的方便, 在下面的论述过程中将
对图像I中的所有相似组G k(k=1, 2, …, N), 进行上述的稀疏表达, 使得图像I可以仅由各字典中的少量原子的线性组合进行较好的重构:
| $ \mathrm{\hat{I}}=\sum\limits_{k=1}^{N}{\mathrm{R}_{k}^{\text{T}}\left( {{D}_{k}}{{\mathrm{ }\!\!\alpha\!\!\text{ }}_{k}} \right)} $ | (3) |
其中:RkT(*) 为Rk(*) 的逆操作, 表示将稀疏表示后的相似组Dkαk置于图像I中对应的位置。
考虑到系数向量的稀疏性, 则基于稀疏表示的图像修复问题可表述为求解优化问题[7]:
| $ \begin{matrix} \min {{\left\| \mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ } \right\|}_{0}} \\ \rm{s}\rm{.t}\rm{.}\ \ \ \ \ \ \left\| \mathit{\boldsymbol{MI}}-\mathit{\boldsymbol{F}} \right\|<\varepsilon \\ \end{matrix} $ | (4) |
其中:α表示N个系数向量的集合{αk|k=1, 2, …, N};M为不可逆的图像降质操作 (这里用模板矩阵表示该操作);I为原始图像;F为受损图像;ε为一个极小的误差容忍阈值。MI表示两个矩阵的点乘, 是对原始图像进行降质。
将式 (3) 代入式 (4), 可以得到稀疏表示数学模型:
| $ \mathit{\boldsymbol{\hat{ }\!\!\alpha\!\!\rm{ }}}=\underset{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}{\mathop{\rm{arg min}}}\, \frac{1}{2}\left\| \mathit{\boldsymbol{M}}\sum\limits_{k=1}^{N}{\mathit{\boldsymbol{R}}_{k}^{\rm{T}}\left( {{D}_{k}}{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}} \right)}-\mathit{\boldsymbol{F}} \right\|_{2}^{2}+\lambda {{\left\| \mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ } \right\|}_{0}} $ | (5) |
其中:第一项为保真项, 第二项为正则项 (惩罚项), λ为比例系数。通过求解目标函数式 (5), 得到N个稀疏的系数向量{αk|k=1, 2, …, N}, 进而对N个相似组进行重构, 由此可以得到修复后的图像
稀疏表示的主要目标是得到原始信号在字典上最稀疏的表示, 即信号可以仅由字典中的少数原子的线性组合近似表示[7], 因此, 构造合适的字典是在稀疏表示框架下进行图像修复的关键[12]。本文提出一种学习自适应字典的方法, 区别于传统的学习字典, 该方法为每个相似组构造不同的字典, 因此具有较强的自适应能力。
考虑到在图像修复的过程中, 原始图像I是未知的, 无法直接通过原图得到相似组Gk, 所以采用Gk的估计量rk进行字典学习, rk的具体含义将在第2章优化部分详细讨论。通过对rk进行奇异值分解 (Singular Value Decomposition, SVD), 得到:
| $ {{\mathit{\boldsymbol{r}}}_{k}}={{\mathit{\boldsymbol{U}}}_{k}}{{\mathit{\boldsymbol{ }}\!\!\Sigma\!\!\rm{ }}_{k}}\mathit{\boldsymbol{V}}_{k}^{\rm{T}}=\sum\limits_{i=1}^{{{n}_{k}}}{{{\gamma }_{k, i}}\left( {{\mathit{\boldsymbol{u}}}_{k, i}}\mathit{\boldsymbol{v}}_{k, i}^{\rm{T}} \right)} $ | (6) |
其中:Σk为对角矩阵, 主对角元素为{γk, 1, γk, 2, …, γk, nk};uk, i、vk, i分别为Uk、Vk的列向量。基于上述分解, 定义字典Dk中的原子为dk, i= uk, i vk, iT(i=1, 2, …, nk), 即:
| $ \begin{align} & {{D}_{k}}=\left\{ {{\mathit{\boldsymbol{d}}}_{k, 1}}, {{\mathit{\boldsymbol{d}}}_{k, 2}}, \cdots, {{\mathit{\boldsymbol{d}}}_{k, {{n}_{k}}}} \right\} \\ & \rm{ }=\left\{ {{\mathit{\boldsymbol{u}}}_{k, 1}}\mathit{\boldsymbol{v}}_{k, 1}^{\rm{T}}, {{\mathit{\boldsymbol{u}}}_{k, 2}}\mathit{\boldsymbol{v}}_{k, 2}^{\rm{T}}, \cdots, {{\mathit{\boldsymbol{u}}}_{k, {{n}_{k}}}}\mathit{\boldsymbol{v}}_{k, {{n}_{k}}}^{\rm{T}} \right\} \\ \end{align} $ | (7) |
基于上述方法构造的字典具有较强的自适应能力, 能够有效地对原始信号进行表达, 其自适应性主要体现在三个方面:1) 字典直接从图像信号中学习得到, 反映图像的本质特征; 2) 不同的相似组Gk对应不同的字典Dk, 区别于传统的方法中, 所有图像块共用一个字典进行稀疏编码; 3) 字典中的原子dk, i(i=1, 2, …, nk) 为与相似组Gk相同尺寸的矩阵, 具有自适应性, 因此能更充分地利用自然图像中图像块之间的相似性先验信息。
2 优化算法经过上述分析, 基于自适应相似组的图像修复问题即为求解优化问题式 (5), 其等价为:
| $ \begin{align} & \ \ \ \ \ \underset{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{, u}}{\mathop{\min }}\, \frac{1}{2}\left\| \mathit{\boldsymbol{Mu}}-\mathit{\boldsymbol{F}} \right\|_{2}^{2}+\lambda {{\left\| \mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ } \right\|}_{0}} \\ & \rm{s}\rm{.t}.\rm{ }\mathit{\boldsymbol{u}}=\sum\limits_{k=1}^{N}{\mathit{\boldsymbol{R}}_{k}^{\rm{T}}\left( {{D}_{k}}{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}} \right)} \\ \end{align} $ | (8) |
该最小化问题为组合优化问题, 不能直接求解, 本文采用SBI (Split Bregman Iteration) 算法[14]进行迭代优化。首先, 将目标函数表示为两个独立的部分: f(u)=0.5‖ Mu-F‖22和g(α)=λ‖α‖0, 然后利用SBI算法对这两个部分进行迭代优化。为了表述方便, 将
初始化 t=0, b(0)= 0, u(0)= 0, α(0)= 0。
For t < T
| $ {{\mathit{\boldsymbol{u}}}^{\left( t+1 \right)}}=\underset{\mathit{\boldsymbol{u}}}{\mathop{\arg \min }}\, f\left( \mathit{\boldsymbol{u}} \right)+\frac{\mu }{2}\left\| \mathit{\boldsymbol{u}}-{{\mathit{\boldsymbol{R}}}^{\rm{T}}}{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}^{\left( t \right)}}-{{\mathit{\boldsymbol{b}}}^{\left( t \right)}} \right\|_{2}^{2} $ | (9) |
| $ {{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}^{\left( t+1 \right)}}=\underset{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}{\mathop{\arg \min }}\, g\left( \mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ } \right)+\frac{\mu }{2}\left\| {{\mathit{\boldsymbol{u}}}^{\left( t+1 \right)}}-{{\mathit{\boldsymbol{R}}}^{\rm{T}}}\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }-{{\mathit{\boldsymbol{b}}}^{\left( t \right)}} \right\|_{2}^{2} $ | (10) |
| $ {{\mathit{\boldsymbol{b}}}^{\left( t+1 \right)}}={{\mathit{\boldsymbol{b}}}^{\left( t \right)}}-\left( {{\mathit{\boldsymbol{u}}}^{\left( t+1 \right)}}-{{\mathit{\boldsymbol{R}}}^{\rm{T}}}{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}^{\left( t+1 \right)}} \right) $ | (11) |
t←t+1
End for
上述迭代过程的关键在于求解最小化问题式 (9) 和式 (10)。对于最小化问题式 (9), 通过令其梯度等于零, 可以容易地得到其对应的解析解:
| $ {{\mathit{\boldsymbol{u}}}^{\left( t+1 \right)}}={{\left( {{\mathit{\boldsymbol{M}}}^{\rm{T}}}\mathit{\boldsymbol{M}}+\mu \mathit{\boldsymbol{E}} \right)}^{-1}}\mathit{\boldsymbol{Q}} $ | (12) |
其中: Q = MTF+μ(RTα(t)+ b(t)); E为单位矩阵。
对于最小化问题式 (10), 其等价为N个子问题[11]:
| $ \underset{{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}}}{\mathop{\arg \min }}\, \frac{1}{2}\left\| {{D}_{k}}{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}}-{{\mathit{\boldsymbol{r}}}_{k}} \right\|_{2}^{2}+\tau {{\left\| {{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}} \right\|}_{0}};k=1, 2, \cdots, N $ | (13) |
其中:τ=240λ/μ为比例系数; r(t+1)= u(t+1)-b(t)为原始图像I的估计; rk=Rk(r(t+1)) 为从估计图像r(t+1)中提取出的相似组, 即1.3节中提到的Gk的估计。
将式 (6) 和式 (7) 代入式 (13), 可得式 (13) 的等价问题:
| $ {{{\mathit{\boldsymbol{\hat{ }\!\!\alpha\!\!\rm{ }}}}}_{k}}=\underset{{{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}}}{\mathop{\arg \min }}\, \frac{1}{2}\left\| {{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}}-{{\mathit{\boldsymbol{ }}\!\!\gamma\!\!\rm{ }}_{k}} \right\|_{2}^{2}+\tau {{\left\| {{\mathit{\boldsymbol{ }}\!\!\alpha\!\!\rm{ }}_{k}} \right\|}_{0}} $ | (14) |
其中:k=1, 2, …, N; γk=[γk, 1, γk, 2, …, γk, nk]为对rk进行SVD后的奇异值向量。因此, 最小化问题式 (14) 具有如下简洁的解析解:
| $ {{{\boldsymbol{\hat{\alpha }}}}_{k}}=hard\left( {{\boldsymbol{\gamma} }_{k}}, \sqrt{2\tau } \right);k=1, 2, \cdots, N $ | (15) |
其中:hard(*) 表示硬阈值操作, 即将γk绝对值小于
基于自适应相似组的图像修复算法描述如下:
输入:降质操作M, 受损图像F。
输出:修复后的图像
初始化 t=0, b(0)= u(0)= 0, α(0)= 0, μ=0.002 5, λ=0.082, τ=240λ/μ, ξ=0.5, β=64, T=25。
For t < T
通过式 (12), 更新u;
图像I的估计: r(t+1)= u(t+1)-b(t);
将r(t+1)分解为N个图像块{ Ψk|k=1, 2, …, N};
For k=1, 2, …, N
基于结构相似性指数得到Ψk的相似图像块;
由相似图像块构造自适应相似组rk;
对相似组rk进行SVD, 构造字典Dk;
通过式 (15), 更新αk;
End for
通过式 (11), 更新b;
t←t+1
End for
3 实验与分析为了验证算法的有效性, 针对随机缺失像素复原、文字去除等方面进行图像修复实验, 并将实验结果和文献[15]算法、GSR算法[11]、文献[16]算法进行对比。采用峰值信噪比 (Peak Signal-to-Noise Ratio, PSNR) 及结构相似性指数 (SSIM)[13]作为图像修复效果的客观评价指标。实验环境:CPU为AMD Athlon X2270 3.42 GHz, 内存为4 GB,系统为Microsoft Windows7, 软件为Matlab R2014a。
3.1 随机缺失像素复原图 2和图 3分别展示了各算法对随机缺失50%像素的Barbara图和Boat图进行修复的效果。通过对比可知, 文献[16]算法不能有效地修复自然图像中的纹理和结构信息, 而文献[15]算法则会导致较严重的图像模糊, 例如图 2中Barbara裤子和围巾上的纹理区域、图 3中的桅杆和绳缆。这主要是由于基于图像块的图像修复算法只考虑单一图像块的修复, 不能较好地保持邻域信息的连贯一致性。相比之下, GSR算法和本文算法修复后的图像取得了较好的视觉效果, 能够同时有效地复原受损图像中的纹理和结构。但是, 由于GSR算法是构造尺寸固定的组, 会引入非相似图像块;而本文采用自适应相似组, 能够有效地排除非相似块的干扰, 准确地构造相似组, 保证修复后的图像具有较好的清晰性。

|
图 2 Barbara图随机缺失50%像素复原 Figure 2 Reconstructed Barbara images with 50% randomly pixels missing |

|
图 3 Boat图随机缺失50%像素复原 Figure 3 Reconstructed Boat images with 50% randomly pixels missing |
为了进一步说明算法的性能, 表 1给出了各算法对8幅图像进行修复后的指标对比, 可以看出, 本文算法较其他三种算法在PSNR和SSIM等客观指标上都有明显的优势。其中, 在峰值信噪比上平均提高了1.07~4.34 dB, 在结构相似性指数上平均提高了0.009 1~0.034 5。
| 表 1 各算法随机缺失像素修复结果对比 Table 1 Inpainting performance comparison of various methods for randomly pixels missing |
图 4为对Lena图进行文字去除的实验效果, 其余图像的实验结果如表 2所示。

|
图 4 文字去除 Figure 4 Text removal |
| 表 2 各算法文字去除结果对比 Table 2 Inpainting performance comparison of various methods for text removal |
可以看出, 对于文字去除实验, 本文算法同样展示出了良好的修复效果, 在峰值信噪比上平均提高了0.94~2.75 dB, 在结构相似性指数上平均提高了0.006 9~0.025 4。在视觉效果方面, 文献[15]算法会引入多余的干扰信息, 例如图 4(c)中Lena的眼睛和帽檐区域, 这是由于基于图像块的图像修复算法, 容易导致错误图像块的产生; 而文献[16]算法和GSR算法则会使得修复区域产生模糊的现象, 如图 4(d)~(e)所示。相比之下, 本文算法能够在不引入多余信息的情况下, 较好地保证结构的连贯性以及纹理的清晰性, 使修复后的图像具有较好的视觉效果。
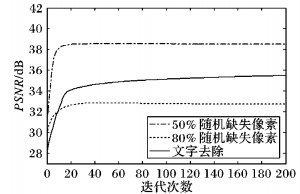
3.3 算法收敛性及算法性能分析图 5为本文算法在50%、80%随机缺失像素修复和文字去除实验中PSNR的变化趋势。
|
图 5 峰值信噪比随迭代次数的变化趋势 Figure 5 Effect of iteration number on PSNR performance |
从图 5可看出, 图像质量先是有明显的改善, 然后趋于收敛, 由此得出本文算法具有快速收敛的特性。对于随机缺失像素修复实验, 只需进行25次迭代, 而对于文字去除实验, 只需40次迭代。这主要是由于本文算法以自适应相似组作为基本单元, 因此能够充分地利用自然图像中的先验信息, 根据图像的本质特征指导图像的修复过程, 从而保证算法的高效性。表 3给出各算法修复一幅512×512图像的平均耗时, 其中修复区域比例为20%。本文算法在修复效率上,是文献[15]算法的2.51倍,是GSR算法的3.32倍。虽然文献[16]算法在修复效率上是最高的, 但是其修复效果远不如本文算法。
| 表 3 各算法平均耗时对比 Table 3 Comparison of computation times |
针对图像修复结果中存在的结构连续性及纹理清晰性较差的问题, 本文在稀疏表示框架下提出了一种基于自适应相似组的图像修复算法。该算法充分利用自然图像中图像块之间的相似性, 构造自适应相似组, 从而对原始图像的本质特征进行准确的描述。实验结果表明, 本文算法在客观评价指标和视觉效果上均有明显的优势, 能够对图像中的纹理信息和结构信息进行有效的修复, 同时具有快速收敛的特性。本文将自适应相似组的概念运用于图像修复, 未来希望能够将这个概念推广到其他的图像处理领域中, 包括图像去噪、图像去模糊以及超分辨率重建等。
| [1] | GUILLEMOT C, LE MEUR O. Image inpainting: overview and recent advances[J]. IEEE Signal Processing Magazine, 2014, 31 (1) : 127-144. doi: 10.1109/MSP.2013.2273004 |
| [2] | CHAN T, SHEN J. Local inpainting models and TV inpainting[J]. SIAM Journal on Applied Mathematics, 2001, 62 (3) : 1019-1043. |
| [3] | CHAN T F, SHEN J. Nontexture inpainting by curvature-driven diffusions[J]. Journal of Visual Communication and Image Representation, 2001, 12 (4) : 436-449. doi: 10.1006/jvci.2001.0487 |
| [4] | RAM I, ELAD M, COHEN I. Image processing using smooth ordering of its patches[J]. IEEE Transactions on Image Processing, 2013, 22 (7) : 2764-2774. doi: 10.1109/TIP.2013.2257813 |
| [5] | WONG A, ORCHARD J. A nonlocal-means approach to exemplar-based inpainting[C]//ICIP 2008: Proceedings of the 15th IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2008: 2600-2603. |
| [6] | CRIMINISI A, PEREZ P, TOYAMA K. Region filling and object removal by exemplar-based image inpainting[J]. IEEE Transactions on Image Processing, 2004, 13 (9) : 1200-1212. doi: 10.1109/TIP.2004.833105 |
| [7] | SHEN B, HU W, ZHANG Y, et al. Image inpainting via sparse representation[C]//ICASSP 2009: Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. Washington, DC: IEEE Computer Society, 2009: 697-700. |
| [8] | LI Z, HE H, YIN Z, et al. A color-gradient patch sparsity based image inpainting algorithm with structure coherence and neighborhood consistency[J]. Signal Processing, 2014, 99 (6) : 116-128. |
| [9] | XU Z, SUN J. Image inpainting by patch propagation using patch sparsity[J]. IEEE Transactions on Image Processing, 2010, 19 (5) : 1153-1165. doi: 10.1109/TIP.2010.2042098 |
| [10] | MAIRAL J, BACH F, PONCE J, et al. Non-local sparse models for image restoration[C]//Proceedings of the 2009 IEEE 12th International Conference on Computer Vision. Piscataway, NJ: IEEE, 2009: 2272-2279. |
| [11] | ZHANG J, ZHAO D, GAO W. Group-based sparse representation for image restoration[J]. IEEE Transactions on Image Processing, 2014, 23 (8) : 3336-3351. doi: 10.1109/TIP.2014.2323127 |
| [12] | XU J, ZHANG L, ZUO W, et al. Patch group based nonlocal self-similarity prior learning for image denoising[C]//Proceedings of the 2015 IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2015: 244-252. |
| [13] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13 (4) : 600-612. doi: 10.1109/TIP.2003.819861 |
| [14] | GOLDSTEIN T, OSHER S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2 (2) : 323-343. doi: 10.1137/080725891 |
| [15] | JIN K H, YE J C. Annihilating filter-based low-rank Hankel matrix approach for image inpainting[J]. IEEE Transactions on Image Processing, 2015, 24 (11) : 3498-3511. doi: 10.1109/TIP.2015.2446943 |
| [16] | AFONSO M V, SANCHES J M R. Blind inpainting using l0 and total variation regularization[J]. IEEE Transactions on Image Processing, 2015, 24 (7) : 2239-2253. doi: 10.1109/TIP.2015.2417505 |




