四旋翼飞行器 (Quadrotor) 具有体积小、重量轻、易于隐蔽等优点, 被广泛应用在农业、军工业维护和侦查探测上[1-2], 成为了目前无人飞行机器人 (Unmanned Aerial Vehicle, UAV) 研究领域的热点问题。微机电系统 (Micro-Electro-Mechanical System, MEMS) 作为四旋翼飞行器惯性测量的主要传感器, 其中的低成本陀螺仪存在漂移积分累计误差[3], 影响了高精度姿态测量的效果, 必须要求多种传感器组合使用, 才能获得较为准确的姿态信息。因而, 多传感器之间的融合滤波算法以及四旋翼飞行器的姿态解算速度和精度直接决定了四旋翼飞行器的飞行质量, 研究精确、快速的姿态解算[4-7]算法成为当前研究热点之一。
针对以上问题, 国内外学者们提出了多种姿态算法。文献[8]提出了一种互补滤波姿态算法, 利用加速度计对陀螺仪漂移误差进行补偿; 但是没有考虑到机体在强机动运动过程中产生的运动加速度和机体振动对加速度计的干扰造成姿态误差变大的问题。相对于文献[8]算法, 文献[9]提出的一种自适应混合滤波算法考虑了机体振动对加速度计的高频噪声, 利用最优重力估计来对参数优化, 消除了加速度的噪声影响; 但是仍然没有对运动加速度进行处理。文献[10]提出了一种定步长的梯度下降姿态估计算法, 通过插值计算出误差函数的极值, 提高了姿态解算的精度。文献[11]则在文献[10]的基础上增加了磁力计, 提出了一种基于梯度下降法的9轴姿态融合算法。这两种梯度下降算法中梯度步长为定值, 当四旋翼飞行器处于高速运动时, 梯度步长过小导致算法动态性能差。但是以上互补和梯度算法均未考虑到系统的噪声和传感器的测量噪声问题。文献[12]提出了一种扩展卡尔曼滤波 (Extended Kalman Filter, EKF) 方程测量模型, 将系统噪声和测量噪声引入状态方程, 进一步提高了姿态解算的精度, 但是在观测方程线性化时引入了线性误差; 对此, 文献[13]提出一种EKF算法, 将梯度下降算法引入EKF算法中, 解决了这种线性化误差, 但是却没有解决运动加速度造成的错误姿态估计影响; 文献[14]提出一种无损卡尔曼滤波器 (Unscented Kalman Filter, UKF), 解决了这种线性化带来的误差; 文献[15]提出了一种基于EKF的算法通过高斯-牛顿法对观测方程非线性观测, 简化了观测方程的计算, 但是没有考虑飞行器运动加速度的影响; 文献[16]提出一种粒子滤波器 (Particle Filter, PF) 算法针对系统噪声为分高斯分布的情况。但是上述UKF和PF的计算量过大, 在低成本的微控制器中不易实现。
本文提出一种改进EKF的四旋翼姿态估计算法。首先, 由陀螺仪输出的角速度通过四元数微分方程得到估计姿态四元数; 然后, 对全球定位系统 (Global Positioning System, GPS) 和加速度计融合后的加速度进行运动加速度抑制处理, 消除运动加速度对姿态估计的影响, 再通过动态步长梯度下降算法得到观测姿态四元数; 然后建立基于四元数的姿态估计滤波方程, 从而完成了微型四旋翼飞行器的水平姿态精确、快速解算; 最后通过磁力计校正并且倾角补偿后单独计算偏航角, 实现了四旋翼飞行器的精确稳定飞行。
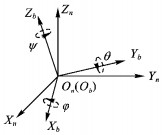
1 姿态参考系统 1.1 姿态坐标系在姿态解算中, 定义两个坐标系——导航坐标系n系和载体坐标系b系来表示姿态角, 其中导航坐标系采用东北天建立坐标系, 导航坐标系的坐标原点O位于运载体的质心。载体坐标系采用右前上建立坐标系, 载体坐标系原点O′与导航坐标系原点O重合。姿态角的定义如图 1所示, 绕X轴旋转对应俯仰角pitch、绕Y轴旋转对应横滚角roll、绕Z轴旋转对应偏航角yaw, 分别为三轴欧拉角φ、θ、ψ。
|
图 1 载体坐标系和导航坐标系 Figure 1 Body coordinate system and navigation coordinate system |
描述导航坐标系和载体坐标系的转换关系通常有三种方法:欧拉角法[17]、方向余弦法[18]、四元数法[19]。但是欧拉角法会在90 °时出现奇点问题, 而余弦矩阵的计算量过大, 因此选用计算量小、算法简单的四元数法描述导航坐标系和载体坐标系的转换关系。捷联惯导系统理论[20]中定义四元数q :
| $ \boldsymbol{q}={{q}_{0}}+{{q}_{1}}{\rm i}+{{q}_{2}}{\rm j}+{{q}_{3}}{\rm k}={{\left[ {{q}_{0}}\;\;\boldsymbol{ }{{q}_{1}}\;\;\boldsymbol{ }{{q}_{2}}\;\;\boldsymbol{ }{{q}_{3}} \right]}^{\text{T}}} $ | (1) |
其中:q0为四元数的标量部分;q1、q2、q3为四元数的矢量部分;i2= j2=k2=-1。定义旋转矩阵为Cbn, 则载体坐标系到导航坐标系的旋转矩阵Cbn可以通过四元数表示为:
| $ \boldsymbol{C}_{b}^{n}=\left[ \begin{align} & 1-2{{q}_{2}^{2}}-2{{q}_{3}^{2}}\boldsymbol{ }2({{q}_{1}}{{q}_{2}}-{{q}_{0}}{{q}_{3}})\boldsymbol{ }2({{q}_{1}}{{q}_{3}}+{{q}_{0}}{{q}_{2}}) \\ & 2({{q}_{1}}{{q}_{2}}+{{q}_{0}}{{q}_{3}})\boldsymbol{ }1-2{{q}_{1}^{2}}-2{{q}_{3}^{2}}\boldsymbol{ }2({{q}_{2}}{{q}_{3}}-{{q}_{0}}{{q}_{1}}) \\ & 2({{q}_{1}}{{q}_{3}}-{{q}_{0}}{{q}_{2}})\boldsymbol{ }2({{q}_{2}}{{q}_{3}}-{{q}_{0}}{{q}_{1}})\boldsymbol{ }1-2{{q}_{1}^{2}}-2{{q}_{2}^{2}} \\ \end{align} \right]\text{ } $ | (2) |
根据z-y-x旋转顺规, 可以求解出三个姿态角:
| $ \left[ \begin{array}{l} \phi \\ \theta \\ \psi \end{array} \right] = \left[ \begin{array}{c} a\tan 2(2{q_2}{q_3} + 2{q_0}{q_1},{q_3^2} - {q_2^2} - {q_1^2} + {q_0^2})\\ - a\sin (2{q_1}{q_3} - 2{q_0}{q_2})\\ a\tan 2(2{q_1}{q_2} + 2{q_0}{q_3},{q_1^2} + {q_0^2} - {q_3^2} - {q_2^2}) \end{array} \right] $ | (3) |
改进EKF姿态估计算法结构原理如图 2所示, 利用加速度计输出值fba和GPS的速度微分输出值fbg对加速度进行补偿得到补偿后的加速度fa-g, 通过运动加速度抑制处理后得到加速度fb, 由动态步长梯度下降算法得出姿态四元数q∇作为卡尔曼滤波器的量测值。由四元数的微分方程对陀螺仪的输出角速率ωb更新得到姿态四元数的估计值q ω。通过磁力计单独估计偏航角, 考虑到环境的复杂性, 在使用磁力计之前对其作了椭球校正和倾角补偿, 即对磁力计输出m作椭圆校正得到mb, 通过倾角补偿后求解偏航角, 最终更新出姿态角pitch、roll、yaw。

|
图 2 改进EKF姿态估计算法原理 Figure 2 Principle of improved EKF attitude estimation algorithm |
四元数微分方程:
| $ {}_{b}^{n}\boldsymbol{\dot{q}}=\frac{1}{2}{}_{b}^{n}\boldsymbol{q}\otimes \boldsymbol{\omega } $ | (4) |
其中:bn q为b系相对n系的四元数, bn
| $ \left[ \begin{array}{l} {{\dot q}_0}\\ {{\dot q}_1}\\ {{\dot q}_2}\\ {{\dot q}_3} \end{array} \right] = \frac{1}{2}\left[ \begin{array}{l} 0{\boldsymbol{ }}\;\; - {\omega _x}{\boldsymbol{ }}\;\; - {\omega _y}{\boldsymbol{ }}\;\; - {\omega _z}\\ {\omega _x}{\boldsymbol{ }}\;\;\;\;0{\boldsymbol{ }}\;\;\;\;\;\;{\omega _z}{\boldsymbol{ }}\;\; \;\;- {\omega _y}\\ {\omega _z}{\boldsymbol{ }}\;\;\;\;{\omega _y}{\boldsymbol{ }} \;\;- {\omega _x}{\boldsymbol{ }}\;\;\;\;0 \end{array} \right]\left[ \begin{array}{l} {q_0}\\ {q_1}\\ {q_2}\\ {q_3} \end{array} \right] $ | (5) |
| $ _{b}^{n}{{\boldsymbol{\dot{q}}}_{k}}=\frac{1}{2}{}_{b}^{n}{{\boldsymbol{q}}_{\left( k-1 \right)}}\otimes \boldsymbol{\omega }_{k}^{b} $ | (6) |
| $ _{b}^{n}{{\boldsymbol{q}}_{k}}=_{b}^{n}{{\boldsymbol{q}}_{\left( k-1 \right)}}+_{b}^{n}{{\boldsymbol{\dot{q}}}_{k}}{{T}_{s}}\text{ } $ | (7) |
由式 (6) 和 (7) 采用先离散后迭代的方法对四元数微分方程进行求解可得k时刻的四元数bn qk, 代入式 (3) 即可得到k时刻的三轴欧拉角φ、θ、ψ。
2.2 加速度补偿算法为了提高加速度的测量精度, 引入了GPS的速度微分信息来补偿加速度计的测量值, 假设GPS提供的加速度输出信息为agxn、agyn、agzn,转换至b系的加速度输出信息为agxb、agyb、agzb。
| $ \left[ \begin{array}{l} a_{gx}^b\\ a_{gy}^b\\ a_{gz}^b \end{array} \right] = {\boldsymbol{C}}_n^b\left[ \begin{array}{l} a_{gx}^n\\ a_{gy}^n\\ a_{gz}^n \end{array} \right] $ | (8) |
得到由GPS补偿后的加速度信息为:
| $ \left[ \begin{array}{l} a_x^b\\ a_y^b\\ a_z^b \end{array} \right] = \left[ \begin{array}{l} a_{ax}^b\\ a_{ay}^b\\ a_{az}^b \end{array} \right] - {\boldsymbol{C}}_n^b\left[ \begin{array}{l} a_{gx}^n\\ a_{gy}^n\\ a_{gz}^n \end{array} \right] $ | (9) |
标准EKF算法是为了解决实际系统中的非线形环节而提出的, 通过对系统方程和量测方程的非线性函数作泰勒级数展开来线性化。这种线性化处理的方式会带来线性化误差[21], 而梯度下降算法的特点之一是可以进行非线性观测, 消除了标准EKF算法中的线性误差, 提高了姿态估计的精度。
梯度下降法是利用目标函数对应的负梯度方向来更新每次迭代的新的方向, 使得每次迭代能使待优化的目标函数逐步减小, 通常用来求解函数的最小值。因此, 将导航坐标系n中重力加速度g通过四元数法旋转到载体坐标系b中的值, 然后减去当前加速度计的测量值作差, 这就是通过加速度计表征的旋转矩阵的误差函数。
重力加速度g在导航坐标系n中的值标准化后为g n=[0, 0, 0, 1]。假设载体坐标系中加速度计的各轴分量为axb、ayb、azb, 那么a b=[0, axb, ayb, azb], 则重力加速度g从导航坐标系n旋转到载体坐标系b:
| $ {{\boldsymbol{g}}^{b}}={}_{n}^{b}\boldsymbol{q}\otimes {{\boldsymbol{g}}^{n}}\otimes {}_{b}^{n}{{\boldsymbol{q}}^{\boldsymbol{*}}} $ | (10) |
其中:g b为向量g在b系中的坐标, nb q为n系相对b系的四元数, nb q *为n系相对b系的复数共轭四元数, g n为向量g在n系中的坐标。
将标准化g n=[0, 0, 0, 1]代入式 (10), 得出重力加速度g在载体坐标系下的值g b, 将其与载体坐标系中的加速度计测量值相减得到误差函数fg(nb q, a b):
| $ {{\boldsymbol{f}}_{g}}\left( {}_{n}^{b}\boldsymbol{q,a} \right)=\left[ \begin{align} & \;\;\;\;2\left( {{q}_{1}}{{q}_{3}}-{{q}_{0}}{{q}_{2}} \right)-a_{x}^{b} \\ & \;\;\;\;2\left( {{q}_{0}}{{q}_{1}}+{{q}_{2}}{{q}_{3}} \right)-a_{y}^{b} \\ & 2\left( {1}/{2}\;-{{q}_{1}^{2}}-{{q}_{2}^{2}} \right)-a_{z}^{b} \\ \end{align} \right] $ | (11) |
对误差函数fg(nb q, a b) 求导后, 得出对应的雅可比矩阵:
| $ {{\boldsymbol{J}}_g}\left( {{}_n^b{\boldsymbol{q}}} \right) = \frac{{d{\boldsymbol{f}_g}}}{{d{}_n^b\boldsymbol{q}}} = \left[ \begin{array}{l} \frac{{\partial {\boldsymbol{f}_{gx}}}}{{d{}_n^b\boldsymbol{q}}}\\ \frac{{\partial {\boldsymbol{f}_{gy}}}}{{d{}_n^b\boldsymbol{q}}}\\ \frac{{\partial {\boldsymbol{f}_{gz}}}}{{d{}_n^b\boldsymbol{q}}} \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} - 2{q_0}\;{\rm{ }}2{q_3}\;{\rm{ }} - 2{q_0}\;{\rm{ }}2{q_1}\\ {\rm{ }}\;\;2{q_1}\;\;{\rm{ }}2{q_0}\;\;\;\;{\rm{ }}2{q_3}\;\;{\rm{ }}2{q_2}\\ {\rm{ }}\;\;\;0{\rm{ }} \;- 4{q_1}\;{\rm{ }} - 4{q_2}\;\;{\rm{ }}0 \end{array} \right] $ | (12) |
通过雅可比矩阵得到误差函数的梯度值。
迭代公式为:
| $ {}_{n}^{b}{{\boldsymbol{q}}_{\nabla }}\left( k \right)={}_{n}^{b}{{\boldsymbol{q}}_{\nabla }}\left( k-1 \right)-\boldsymbol{\mu} \frac{\nabla {{\boldsymbol{f}}_{g}}\left( {}_{n}^{b}\boldsymbol{q,}{{\boldsymbol{a}}^{b}} \right)}{\left\| \left. \nabla {{\boldsymbol{f}}_{g}}\left( {}_{n}^{b}\boldsymbol{q,}{{\boldsymbol{a}}^{b}} \right) \right\| \right.} $ | (13) |
其中:nb q∇(k) 为梯度下降法所求的目标姿态四元数; nb q∇(k-1) 为迭代的上一次姿态四元数估计值; μ为梯度下降法的步长;
迭代式 (13) 即从初始时刻的姿态沿负梯度方向更新到误差函数的极值点, 即为所求的姿态四元数。
梯度步长直接描述了算法的性能:当且仅当算法的收敛速度比运载体实际运行速度快时, 解算结果才正确。而固定的梯度步长只能满足一定速率下的算法精度, 所以当物体处于高速转体运动时, 算法步长过小, 导致姿态估计结果错误。
因此提出了动态步长的梯度下降算法, 该步长的大小正比于实际物理的运动合角速度模长。当物体慢速运动时, 梯度步长较小, 满足算法静态精度; 而当物体快速运动时, 梯度步长增加。步长μ与载体运动的角速度、系统的采样时间正相关:
| $ \boldsymbol{\mu} \sim \alpha \left\| \boldsymbol{\omega} \right\|{{T}_{s}} $ | (14) |
其中:‖ ω ‖为载体的运动角速度模长; Ts为系统的采样时间; α > 1。式 (14) 表明载体的运动角速度越快, 采样时间越长, 那么梯度的步长也就越长。
载体的运动角速度即为陀螺仪的测量角速度。假设陀螺仪的测量角速度为:
| $ \boldsymbol{\omega }=\left[ {{\omega }_{x}}\text{ }{{\omega }_{y}}\text{ }{{\omega }_{z}} \right] $ |
则载体的运动角速度模长为:
| $ \left\| \boldsymbol{\omega} \right\|=\sqrt{(\omega {{_{x}^{b}})^{2}}+(\omega {{_{y}^{b}})^{2}}+(\omega {{_{z}^{b}})^{2}}}\text{ } $ | (15) |
为避免静态或者低速运动时ω=0而导致动态步长为0的结果, 这里给动态步长补一个初始值μ0, 该初始值μ0通过静态测试实验得出, 因此梯度下降法中的动态步长为:
| $ \mu \text{=}{{\mu }_{0}}\text{+}\alpha {{T}_{s}}\sqrt{(\omega {{_{x}^{b}})^{2}}+(\omega {{_{y}^{b}})^{2}}+(\omega {{_{z}^{b}})^{2}}}\text{ } $ | (16) |
在动态梯度下降算法中, 通过加速度计表征的旋转矩阵误差为导航坐标系n中的重力加速度g n旋转到载体坐标系b中的向量g b与加速度计测量值的差。因此载体坐标系中加速度计的测量值只能存在重力加速度, 但是飞行器在强机动情况下会产生运动加速度, 会降低姿态解算的精度。所以要把飞行器的重力加速度和运动加速度分离开来处理, 如果运动加速度的值过大, 式 (13) 中本次迭代的加速度计更新出来的四元数应该减小。所以运动加速度越大, 算法对加速度计测量值的不信任程度越深。
定义δk为加速度计测量值的信任程度因子:
| $ {{\delta }_{k}}={\varepsilon }/{\left( \varepsilon \text{+}\left\| {{\boldsymbol{a}_{s}}^{b}}_{k} \right\| \right)}\; $ | (17) |
其中:‖ asb k‖为运动加速度的模长, ε为信任因子的可调参数。式 (17) 表明运动加速度的值越大, 信任因子越低。运动加速度向量为a sb k为:
| $ {{\boldsymbol{a}_{s}}^{b}}_{k}={{\boldsymbol{a}}^{b}}_{k}-\boldsymbol{g}{{\left[ C{{_{b}^{n}}_{31}}\text{ }C{{_{b}^{n}}_{32}}\text{ }C{{_{b}^{n}}_{33}} \right]}^{\text{T}}_{\left. k \right|k-1}} $ | (18) |
其中:akb为当前加速度计的测量值; g为重力加速度。
为了消除加速度计测量值对姿态解算的影响, 式 (18) 中, [Cb31n, Cb32n, Cb33n]k|k-1T为上一次的卡尔曼滤波器的输出姿态增量。如式 (19) 所示:
| $ {}_{n}^{b}{{\boldsymbol{q}}_{\nabla }}\left( k \right)={}_{n}^{b}{{\boldsymbol{q}}_{\nabla }}\left( k-1 \right)-{{\delta }_{k}}*\mu \frac{\nabla {{\boldsymbol{f}}_{g}}\left( {}_{n}^{b}\boldsymbol{q,}{{\boldsymbol{a}}^{b}} \right)}{\left\| \left. \nabla {{\boldsymbol{f}}_{g}}\left( {}_{n}^{b}\boldsymbol{q,}{{\boldsymbol{a}}^{b}} \right) \right\| \right.} $ | (19) |
其中:
标准EKF算法是为了解决实际系统中的许多非线性环节而出现的算法, 通过对系统方程和量测方程的非线性函数作泰勒级数展开并保留其中的线性项, 从而获得线性模型。
建立如下模型:
| $ \left\{ \begin{align} & {{{\boldsymbol{\hat{X}}}}_{k}}={{\boldsymbol{A}}_{k}}{{\boldsymbol{X}}_{k-1}}+{{\boldsymbol{W}}_{k}} \\ & {{\boldsymbol{Z}}_{k}}={{\boldsymbol{H}}_{k}}{{{\boldsymbol{\hat{X}}}}_{k}}+{{\boldsymbol{V}}_{k}} \\ \end{align} \right. $ | (20) |
其中: Ak为状态转移矩阵;Z k为观测量;Hk为观测阵;Wk为系统噪声矩阵;Vk为测量噪声矩阵。Wk和Vk满足:
| $ \left\{ \begin{align} & E[{{\boldsymbol{W}}_{k}}]=0\text{ };\;\;E[{{\boldsymbol{W}}_{k}}\boldsymbol{W}_{k}^{\text{T}}]={{\boldsymbol{Q}}_{k}} \\ & E[{{\boldsymbol{V}}_{k}}]=0\text{ };\;\;E[{{\boldsymbol{V}}_{k}}\boldsymbol{V}_{k}^{\text{T}}]={{\boldsymbol{R}}_{k}} \\ \end{align} \right. $ | (21) |
其中: Qk为系统噪声方差矩阵;Rk为测量噪声矩阵。
3.1 过程模型选用4D四元数作为状态变量, 根据式 (4) 四元数的微分方程得到系统的状态方程:
| $ \left[ \begin{array}{l} {{\dot x}_1}\\ {{\dot x}_2}\\ {{\dot x}_3}\\ {{\dot x}_4} \end{array} \right] = \frac{1}{2}\left[ \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right] \otimes \left[ \begin{array}{c} 0\\ \omega _x^b\\ \omega _y^b\\ \omega _z^b \end{array} \right] $ | (22) |
式 (22) 用四元数表示即为:
| $ \boldsymbol{\dot{q}}={{\mathit{\pmb{\Omega}}}^{b}}\boldsymbol{q}=\left[ \begin{align} & 0\text{ }-\frac{\omega _{x}^{b}}{2}\; -\frac{\omega _{y}^{b}}{2}\text{ -}\frac{\omega _{z}^{b}}{2} \\ & \frac{\omega _{x}^{b}}{2}\;\; 0\;\;-\frac{\omega _{z}^{b}}{2}\;\;\frac{\omega _{y}^{b}}{2}\text{ } \\ & \frac{\omega _{y}^{b}}{2}\;\frac{\omega _{z}^{b}}{2}\;\; 0 \;\;-\frac{\omega _{x}^{b}}{2} \\ & \frac{\omega _{z}^{b}}{2}\;-\frac{\omega _{y}^{b}}{2}\text{ }\frac{\omega _{x}^{b}}{2}\;\; 0\;\; \\ \end{align} \right]\boldsymbol{q} $ | (23) |
对式 (23) 的求解, 此处采用离散化处理求解, 设系统的采样周期为Ts, 离散化后的状态方程为:
| $ {{\boldsymbol{q}}_{k}}=\exp (\mathit{\pmb{\Omega}}_{k-1}^{b}{{T}_{s}}){{\boldsymbol{q}}_{k-1}}\text{ }k=1,2,... $ | (24) |
为了方便计算, 对上述exp (Ωk-1bTs) 进行泰勒级数展开, 并且保留二阶项得到:
| $ {{\boldsymbol{q}}_{k}}=\left[ {{I}_{3\times 3}}\left( 1-\frac{\Delta {{\theta ^{2}}}}{8} \right)+\frac{1}{2}\mathit{\pmb{\Omega}}_{k-1}^{b}{{T}_{s}} \right]{{\boldsymbol{q}}_{k-1}}\text{ } $ | (25) |
其中:E[Wk WkT]=σg2 I。
由于陀螺仪的输出角速度作为状态转移矩阵的变量, 因此对陀螺仪进行如下建模:
| $ {{\boldsymbol{\omega }}^{b}}\text{=}{{\boldsymbol{\omega }}_{\text{real}}}+{}^{g}\boldsymbol{b}+{}^{g}\boldsymbol{w} $ | (26) |
其中: ω b为陀螺仪的测量角速度;ωreal为载体的真实角速度;g b为陀螺仪的漂移偏差;g w为陀螺仪的测量噪声, 满足式 (21), 并且协方差矩阵为E[Wk WkT]=σg2 I。由于实际环境中温度基本恒定不变, 因此可以假设陀螺仪的而漂移偏差g b是一个常量。
| $ {{\boldsymbol{q}}_{k}}=A\left( \mathit{\pmb{\Omega}}_{k-1}^{b},{{T}_{s}} \right){{\boldsymbol{q}}_{k-1}}+{}^{q}{{\boldsymbol{w}}_{k-1}}=\\ \;\;\;\;\;\;\;\left[ {{\boldsymbol{I}}_{3\times 3}}\left( 1-\frac{\Delta {{\theta ^{2}}}}{8} \right)+\frac{1}{2}\boldsymbol{\Omega }_{k-1}^{b}{{T}_{s}} \right]{{\boldsymbol{q}}_{k-1}}\text{+}{}^{q}{{\boldsymbol{w}}_{k-1}} $ | (27) |
陀螺仪过程噪声为:
| $ {}^{q}{{\boldsymbol{w}}_{k-1}}=-\frac{{{T}_{s}}}{2}{{\boldsymbol{\Xi} }_{k-1}}{}^{q}{{\boldsymbol{w}}_{k-1}}=-\frac{{{T}_{s}}}{2}\left[ \begin{matrix} \left[ {{\boldsymbol{e}}_{k-1}}\times \right]+{{q}_{0}}{{\boldsymbol{I}}_{3\times 3}} \\ -\boldsymbol{e}_{k-1}^{\text{T}} \\ \end{matrix} \right]{}^{g}\boldsymbol{w} $ | (28) |
其中:ek-1=[q1, k,q2, k,q3, k]T;[ek-1×]为ek-1的反对称矩阵。由于陀螺仪的测量噪声g w和采样时间Ts足够小, 使得式 (28) 近似成立。所以可以求出系统过程噪声方差阵:
| $ {{\boldsymbol{Q}}_{k}}={{\left( \frac{{{T}_{s}}}{2} \right)^{2}}}{{\boldsymbol{\Xi} }_{k}}\sigma _{g^{2}}\boldsymbol{I}\boldsymbol{\Xi} _{k}^{T}\text{ } $ | (29) |
标准EKF算法在建立观测模型时需要对非线性函数在先验密度处求偏导来将非线性化方程化为线性化方程;但是这种线性化方式会引入线性误差, 造成姿态估计的精度降低。因此将可以进行非线性观测的梯度下降算法引入卡尔曼滤波器, 避免了线性化, 提高了姿态估计的精度。
为了满足梯度下降算法的实时性和快速性, 将动态步长引入梯度下降算法中; 为了提高加速度的输出测量精度, 采用两步优化法:1) 引入了GPS的速度微分信息来补偿加速度计的测量值, 从而提高了加速度测量值的精确度; 2) 对强机动情况下产生的运动加速度进行抑制处理, 提高了加速度输出测量值的准确性。
综上所述, 本文将GPS、加速度计融合的运动加速度抑制的动态步长梯度下降算法引入卡尔曼滤波器中, 使得观测模型简化为:
| $ {{\boldsymbol{z}}_{i}}={{\boldsymbol{q}}_{\nabla ,i-1}}={{\boldsymbol{x}}_{i}}+{{\boldsymbol{v}}_{i}},\text{ }i=1,2,3.4 $ | (30) |
其中: q∇, i-1为引入卡尔曼的梯度下降法计算出的观测姿态四元数, 由于该过程由加速度计测量输出, 因此观测模型的噪声方差阵即由加速度计的测量噪声vk决定, 也即vi= vk。由式 (21) 可得: Rk=E[VkVkT]。此时的观测阵Hk即可简化为:
| $ {{\boldsymbol{H}}_{k}}={{\boldsymbol{I}}_{4\times 4}} $ | (31) |
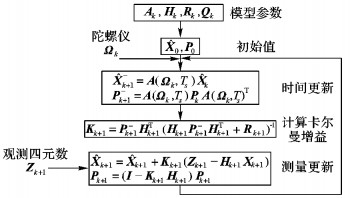
由卡尔曼滤波器的5个基本算法方程, 本文提出的一种改进EKF姿态估计算法的原理框图如图 3所示。
|
图 3 改进EKF姿态估计算法原理框图 Figure 3 Principle diagram of improved EKF attitude estimation |
由于磁力计容易受到磁场干扰源干扰, 为了避免磁力计对水平姿态造成错误干扰, 前面的算法中并没有将磁力计的数据加入到卡尔曼滤波器中,而是对磁力计进行椭球校正补偿后, 再进行倾角补偿, 最终单独计算偏航角,增强了姿态的抗磁干扰性能。
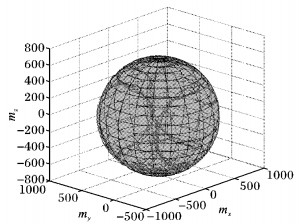
校正磁力计的方法:假设空间中地磁场的磁感线是垂直指向地面的, 让飞行器的X、Y、Z轴的正反6个方向依次指向这条垂线的方向, 缓慢匀速地转动飞行器, 采集磁力计的输出数据;根据6次的采集数据在Matlab上拟合出球体, 并求出球心坐标, 从而校正偏差。
坐标原点即为图中的“*”所在的位置, 从图 4可以看出球心并不在坐标原点, 所以进行硬磁校正。由图 4得到的磁力计X、Y、Z三轴偏差硬磁校正数据为-5.546、214.661、-81.502。
|
图 4 磁力计球形拟合 Figure 4 Magnetometer spherical fitting |
假设校正后的磁力计输出m b= [0,mxb, myb, mzb]T, 通过倾角补偿后的结果为:
| $ \left[ \begin{array}{l} m_{cx}^b\\ m_{cy}^b\\ m_{cz}^b \end{array} \right] = \left[ \begin{array}{l} m_x^b\cos \phi - m_z^b\sin \phi \\ m_x^b\sin \theta \sin \phi + m_y^b\cos \theta + m_z^b\sin \theta \cos \phi \\ m_x^b\cos \theta \sin \phi - m_y^b\sin \theta + m_z^b\cos \theta \cos \phi \end{array} \right] $ | (32) |
其中:θ为改进EKF估计出来的姿态横滚角roll; φ为改进EKF滤波估计出来的姿态俯仰角pitch。
最终的姿态偏航角即可以由倾角补偿后的磁力计输出数据计算得到:
| $ \psi =\arctan \left( \frac{m_{cy}^{b}}{m_{cx}^{b}} \right) $ | (33) |
综上所述, 本文提出的改进EKF四旋翼姿态估计完整算法组建完毕。
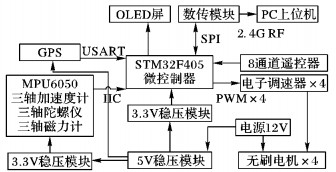
4 实验测试与结果分析 4.1 实验测试平台本文实验平台选用以ARM-CortexM3为内核的STM32F405、32位微处理器来搭建的微型四旋翼飞行器。惯性导航传感器选用美国体感技术公司Inven Sense的MPU6050, 该模块为集成三轴加速度计、三轴陀螺仪、三轴磁力计的EMES传感器。系统的结构示意图如图 5所示。
|
图 5 四旋翼飞行器实验平台系统结构 Figure 5 System structure of experimental platform for quadrotor |
图 5中四旋翼的飞行器实验平台有遥控器、数传模块、GPS模块、惯性导航传感器MPU6050、电机驱动模块、无刷电机、OLED显示模块、电源及稳压模块组成。
四旋翼飞行器的各项参数如表 1所示。表 1中:电机尺寸2208代表电机定子内径为22 mm, 定子厚度为8 mm;电机KV值的大小代表转速和力矩的信息。
| 表 1 四旋翼飞行器的各项参数 Table 1 Parameters of quadrotor |
为了验证改进EKF姿态估计算法的性能,进行了以下五组对比实验:第一组为静态实验, 用来测试算法的静态性能;第二组实验为抗磁干扰实验, 用来验证算法在有磁场干扰时, 水平姿态解算的精度;第三组实验为水平滑动实验, 用来测试四旋翼在强机动情况下有了运动加速度后, 改进EKF中加速度抑制处理算法对姿态解算的影响;第四组实验为绕轴旋转实验, 用来测试飞行器在高速运动情况下动态步长对姿态解算的动态性能影响;第五组实验为四旋翼不水平时测试偏航角实验, 用来验证算法在四旋翼不水平时偏航角的精度。
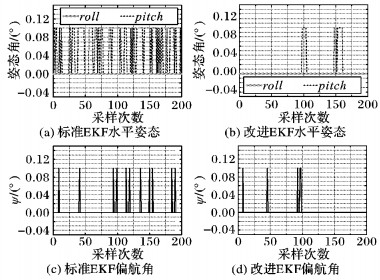
在实验平台静止时, 同时用两种姿态算法解算出飞行器的姿态并统计俯仰角和横滚角的数据进行对比,结果如图 6所示。由图 6中的姿态波形对比得出两种算法得到的姿态角波动范围均为0°~0.1°, 但是改进EKF算法得到的姿态波动性较小。表 2给出了两种算法姿态角的均方根误差、最大值以及最小值, 得到静态时改进EKF算法的姿态解算精度高于标准EKF算法。通过静态测试实验可知,由于加速度融合了加速度计和GPS, 因此姿态更加稳定。
|
图 6 静态测试下两种姿态算法的结果 Figure 6 Static test results of two attitude algorithms |
| 表 2 静态测试下两种算法的姿态误差表 Table 2 Attitude estimation errors of two algorithms in static test |
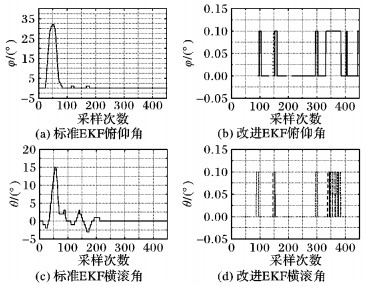
在四旋翼飞行器静止时用一根通电导线模拟磁场干扰源在四旋翼实验平台飞控板上方从左往右划过, 保持飞行器静止。同时用两种算法测得这期间的水平姿态角如图 7所示。图 7中可以明显观察出, 在有了磁场干扰后, 标准EKF算法受到了较大的影响, 而改进EKF算法基本上不受磁场干扰的影响。通过磁场干扰实验可以得出, 改进EKF算法水平姿态分离磁力计后, 明显增强了而抗干扰能力, 提高了水平姿态的解算精度。
|
图 7 抗磁干扰实验结果 Figure 7 Anti-magnetic interference test results |
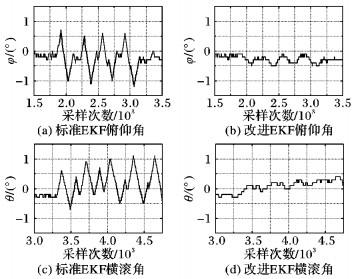
四旋翼实验平台沿Y轴水平来回快速运动4次, 然后沿X轴水平来回快速运动4次, 同时用两种姿态算法解算出飞行器的姿态并统计俯仰角和横滚角的数据进行对比,结果如图 8所示。从图 8中标准EKF算法和改进EKF下测得的roll和pitch的数据对比波形可以得出在飞行器有了运动加速度后, 会对标准EKF算法姿态解算造成较大误差, 而改进的EKF算法姿态解算几乎不受运动加速度影响。表 3给出水平滑动实验测试下两种算法得到的姿态角均方根误差、最大值和最小值。由表中数据得到, 在水平滑动实验测试下, 改进EKF算法得到的姿态角误差明显小于标准EKF算法得到的姿态角; 并且姿态的波动范围小。
|
图 8 水平滑动测试两种算法的结果 Figure 8 Horizontal slip test results of two attitude algorithms |
| 表 3 水平滑动下两种算法姿态角的误差 Table 3 Attitude estimation errors of two algorithms in horizontal slip test |
通过第二组水平滑动测试实验得到, 水平滑动测试下改进EKF算法优于标准EKF算法。说明了对运动加速度抑制处理会在强机动情况下提高姿态解算的精度, 并且增强了姿态的抗干扰性。
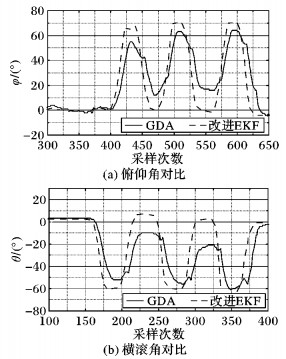
将四旋翼实验平台绕X轴旋转70°,即增大pitch到70°然后减小pitch到0°静止, 重复以上运动3次;再将四旋翼实验平台绕Y轴旋转-60°,即减小roll到-60°然后增大roll到0°静止, 重复以上运动3次。同时用固定步长的梯度下降算法 (Gradient Descent Algorithm, GDA) 和标准EKF姿态算法解算出飞行器的姿态并统计俯仰角和横滚角的数据进行对比, 结果如图 9所示。从GDA和改进EKF算法形成2组对比实验中得出, 在旋转过程中GDA下姿态角度跟随相较改进EKF算法不仅存在明显滞后, 并且精度上也存在较大误差。在绕轴旋转测试下, GDA姿态跟随的平均滞后时间为106 ms, 改进EKF算法为48 ms。这说明改进EKF算法中动态步长梯度下降算法姿态跟踪性能优于定步长姿态下降算法,即动态步长的梯度下降算法动态性能和精度比定步长梯度下降姿态算法好。
|
图 9 动态绕轴测试下两种算法结果 Figure 9 Rotation test results of two attitude algorithms |
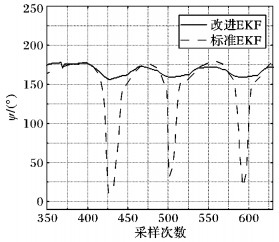
在四旋翼实验平台不水平并且保持偏航角为180°时, 即快速旋转将pitch增大至70°后再减小至0°, 完成偏航角倾角补偿实验, 同时用两种算法测得这期间的偏航角yaw的数据, 结果如图 10所示。从图 10中的两种算法对比波形可以观测出, 标准EKF算法没有对磁力计进行倾角补偿, 所以在四旋翼不水平时, 偏航角的数据出现了较大误差;而改进EKF在四旋翼不水平时对偏航角进行了补偿, 所以偏航角基本上无偏差。
|
图 10 两种算法偏航角输出结果 Figure 10 yaw results of two attitude algorithms |
本文提出了一种改进EKF四旋翼姿态算法, 将运动加速度抑制的动态步长梯度下降算法融入扩展卡尔曼中, 提高了四旋翼姿态解算的精确度和快速性, 并且增强了姿态的抗干扰性。该算法与标准EKF算法和GDA在四旋翼实验平台上, 分别完成静态实验、抗磁干扰实验、水平运动实验、绕轴运动实验和偏航角倾角补偿实验。实验结果表明:改进EKF算法在静态时提高了加速度计的输出精度; 在强机动情况下。抑制了运动加速度, 提高了姿态解算的精度; 在高速运动情况下的动态步长增强了算法的动态性能, 实现了对四旋翼飞行器姿态的实时跟踪; 增强了水平姿态的抗干扰性, 提高了偏航角的准确性。
| [1] | PRIMICERIO J, GENNARO S F D, FIORILLO E, GENESIO L, et al. A flexible unmanned aerial vehicle for precision agriculture[J]. Precision Agriculture, 2012, 13 (4) : 517-523. doi: 10.1007/s11119-012-9257-6 |
| [2] | 张静, 霍建文, 刘星, 等. 微型四旋翼飞行侦察机器人控制系统设计[J]. 测控技术, 2015, 34 (7) : 67-69. ( ZHANG J, HUO J W, LIU X, et al. Design of a micro-quadrotor reconnaissance robot control system[J]. Measurement and Control Technology, 2015, 34 (7) : 67-69. ) |
| [3] | 杨克虎, 史英桂, 姬靖, 等. 基于低成本磁场和MEMS惯性传感器的姿态测定系统[J]. 中国惯性技术学报, 2008, 16 (5) : 556-562. ( YANG K H, SHI Y G, JI J, et al. Attitude determination system with low cost magnetic and MEMS inertial sensors[J]. Journal of Chinese Inertial Technology, 2008, 16 (5) : 556-562. ) |
| [4] | DI L, FROMM T, CHEN Y. A data fusion system for attitude estimation of low-cost miniature UAVs[J]. Journal of Intelligent & Robotic Systems, 2012, 65 (1/2/3/4) : 621-635. |
| [5] | MADGWICK S O H. An efficient orientation filter for inertial and inertial /magnetic sensor arrays[EB/OL].[2016-03-10]. https://www.samba.org/tridge/UAV/madgwick_internal_report.pdf. |
| [6] | MADGWICK S O H, HARRISON A J L, VAIDYANATHAN R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics. Piscataway, NJ: IEEE, 2011:1-7. |
| [7] | 张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16 (10) : 1963-1970. ( ZHANG R H, JIA H G, CHEN T, et al. Attitude solution for strapdown inertial navigation system based on quaternion algorithm[J]. Optics and Precision Engineering, 2008, 16 (10) : 1963-1970. ) |
| [8] | 王立, 章政, 孙平. 一种自适应互补滤波姿态估计算法[J]. 控制工程, 2015, 22 (5) : 881-886. ( WANG L, ZHANG Z, SUN P. An adaptive complementary filter for attitude estimation[J]. Control Engineering of China, 2015, 22 (5) : 881-886. ) |
| [9] | 傅忠云, 刘文波, 孙金秋, 等. 自适应混合滤波算法在微型飞行器姿态估计中的应用[J]. 传感技术学报, 2014, 27 (5) : 698-703. ( FU Z Y, LIU W B, SUN J Q, et al. Application of adaptive hybrid filter algorithm in the estimation of the micro air vehicle attitude[J]. Chinese Journal of Sensors and Actuators, 2014, 27 (5) : 698-703. ) |
| [10] | 冀亮, 钱正洪, 白茹. 基于四元数的四轴无人机姿态的估计和控制[J]. 现代电子技术, 2015 (11) : 112-116. ( JI L, QIAN Z H, BAI R. Attitude estimation and control of quaternion based quad-axis UAV[J]. Modern Electronics Technique, 2015 (11) : 112-116. ) |
| [11] | 彭孝东, 张铁民, 李继宇, 等. 基于传感器校正与融合的农用小型无人机姿态估计算法[J]. 自动化学报, 2015, 41 (4) : 854-860. ( PENG X D, ZHANG T M, LI J Y, et al. Attitude estimation algorithm of agricultural small-UAV based on sensors fusion and calibration[J]. Acta Automatica Sinica, 2015, 41 (4) : 854-860. ) |
| [12] | SABATINI A M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing[J]. IEEE Transactions on Biomedical Engineering, 2006, 53 (7) : 1346-1356. doi: 10.1109/TBME.2006.875664 |
| [13] | WANG L, ZHANG Z, SUN P. Quaternion-based Kalman filter for AHRS using an adaptive-step gradient descent algorithm[J/OL].[2016-05-10].International Journal of Advanced Robotic Systems, 2015.http://journals.sagepub.com/doi/pdf/10.5772/61313. |
| [14] | ENAYATI N, DE MOMI E, FERRIGNO G. A quaternion-based unscented Kalman filter for robust optical/inertial motion tracking in computer-assisted surgery[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64 (8) : 2291-2301. |
| [15] | YUN X, LIZARRAGA M, BACHMANN E R, et al. An improved quaternion-based Kalman filter for real-time tracking of rigid body orientation[C]//Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE, 2003:1074-1079. |
| [16] | 曲仕茹, 马志强. 改进的粒子滤波在四旋翼姿态估计中的应用[J]. 飞行力学, 2013, 31 (5) : 458-461. ( QU S R, MA Z Q. Application of the improved particle filter to quad-rotor aircraft's attitude estimation[J]. Flight Dynamics, 2013, 31 (5) : 458-461. ) |
| [17] | 周绍磊, 丛源材, 李娟, 等. 方向余弦矩阵中四元数提取算法比较[J]. 中国惯性技术学报, 2008, 16 (4) : 415-418. ( ZHOU S L, CONG Y C, LI J, et al. Comparison of algorithms for extracting quaternion from DCM[J]. Journal of Chinese Inertial Technology, 2008, 16 (4) : 415-418. ) |
| [18] | 蒋钰, 谌海云, 岑汝平. 基于四元数的四旋翼飞行器姿态解算算法[J]. 制造业自动化, 2015, 37 (23) : 77-80. ( JIANG Y, CHEN H Y, CEN R P. Attitude solution algorithm for four rotor aircraft based on four element number[J]. Manufacturing Automation, 2015, 37 (23) : 77-80. ) |
| [19] | 陈哲. 捷联惯导系统原理[M]. 北京: 中国宇航出版社, 1986 . ( CHEN Z. Strapdown Inertial Navigation System[M]. Beijing: China Astronautic Publishing House, 1986 . ) |
| [20] | 秦永元. 惯性导航[M]. 北京: 科学出版社, 2014 : 288 -299. ( QIN Y Y. Inertial Navigation[M]. Beijing: Science Press, 2014 : 288 -299. ) |
| [21] | 王立. 基于北斗/GPS导航的视觉着陆四旋翼飞行器设计[D]. 武汉: 武汉科技大学, 2016. ( WANG L. Design of a Beidou/GPS quadrotor with vision-based landing[D]. Wuhan: Wuhan University of Science and Technology, 2016. ) |




