拖挂式移动机器人 (tractor-trailer mobile robots) 是由机器人 (牵引车) 以铰接等形式挂接若干拖车组合而成。这类机器人系统一般通过正、倒车和转向驱动, 带动拖车完成指定运输任务, 通常被用于港口码头、自动化工厂、车站、酒店、核环境等场所, 能代替人力执行一些危险或精度要求高的物资运输工作。研究拖挂式机器人涉及的领域十分广泛, 包括运动学建模、运动规划、路径跟踪、可控性分析等。与自由运动的单体机器人不同, 拖挂式移动机器人系统是一个具有高复杂性和高综合性的非完整、欠驱动、非线性系统, 因此, 一直是机器人领域研究的热点和难点。
路径跟踪是通过设计合理的控制方法, 实现机器人按照指定路径完成行进动作。拖挂式机器人系统根据连接方式可分为离轴式和连轴式, 根据运动特性又可分为正车和倒车, 由于系统结构的复杂性, 不同工况下系统的路径跟踪控制方法[1]都各不相同, 尤其针对离轴式倒车系统, 通常容易发生牵引车和拖车折叠、挤压的现象。因此, 控制方法的好坏将直接影响拖挂式移动机器人在跟踪路径上的安全性和稳定性。
路径规划是指机器人从所处的环境中自动搜索出一条从初始状态到目标状态的避碰、最优或次优路径。通常选用的算法包括人工势场 (Artificial Potential Field) 法、遗传算法 (Genetic Algorithm,GA)、蚁群优化 (Ant Colony Optimization, ACO) 算法[2]、模拟退火算法 (Simulated Annealing,SA)、快速扩展随机树 (Rapid-exploring Random Tree, RRT) 算法等。巩敦卫等[3]基于改进模拟退火算法, 针对全局静态移动机器人, 通过引入脱障算子和一致寻优算子, 提出提出了一种新的状态产生方法, 提高了寻优效率和全局寻优能力。刘传领[4]基于势场法和遗传算法, 针对单体移动机器人的路径规划算法, 提出了一些改进的及新的解决方案, 以提高算法的计算效率, 扩展其使用范围。杜明博等[5]针对车辆路径规划问题, 基于快速扩展随机树算法, 采用目标偏向采样策略以及连续曲率后处理技术实现了车辆连续轨迹的生成, 但降低了算法的稳定性和计算速度。
拖挂式移动机器人属于多主体系统, 在约束和控制方法上相对复杂, 一般的单体无约束机器人的路径规划算法无法满足实际需求。本文在基本RRT算法[6]中嵌入了该系统的路径跟踪控制技术, 并加入了样条曲线拟合、节点击中机制、贪心 (Greedy) 优化[7]等算法, 得到一种符合系统运动学特性的新型规划算法。在此基础上, 通过VC + +开发完成了可交互的拖挂式移动机器人路径规划软件, 验证了算法的准确性和可靠性。
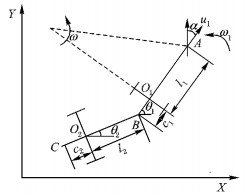
1 路径跟踪控制方法 1.1 运动学模型根据带一节拖车的拖挂式移动机器人系统, 建立运动学模型, 如图 1所示。
|
图 1 拖挂式移动机器人系统示意图 Figure 1 Diagram of the tractor trailer mobile robot system |
牵引车 (根据系统动力源, 统称牵引机器人为牵引车) 的姿态可描述为 (x1, y1, z1), 拖车的姿态可描述为 (x2, y2, z2)。设牵引车前轮与车体纵轴的夹角 (即车轮转向角) 为α, 逆时针为正。设牵引车的线速度 (前进速度) 和角速度分别为u1和ω1(或
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {u_1}{\rm{cos}}{\theta _1}\\ {{\dot y}_1} = {u_1}{\rm{sin}}{\theta _1}\\ {{\dot q}_1} = {w_1}\\ {{\dot q}_2} = [{u_1}{\rm{sin}}({\theta _1} - {\theta _2}) - {c_1}{w_1}{\rm{cos}}({\theta _1} - {\theta _2})]/{l_2} \end{array} \right. $ | (1) |
根据拖车和牵引车的连接几何关系可得:
| $ \left\{ \begin{array}{l} {x_2} = {x_1} - {c_1}{\rm{cos}}{\theta _1} - {l_2}{\rm{cos}}{\theta _2}\\ {y_2} = {y_1} - {c_1}{\rm{sin}}{\theta _1} - {l_2}{\rm{sin}}{\theta _2} \end{array} \right. $ | (2) |
本文主要研究带一节拖车的单体两轮机器人系统模型。
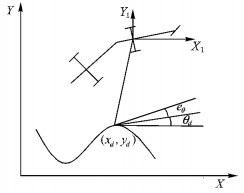
|
图 2 路径跟踪示意图 Figure 2 Diagram of path-following method |
根据系统连接方式的不同, 拖挂式机器人系统可分为离轴式 (c1 > 0) 和连轴式 (c1=0), 两种连接方式在正车驱动中的运动方程相同, 故可用相同的控制方法进行路径跟踪。
根据文献[8, 10]可知:设期望路径为ρd(xd, yd)、xd和yd三阶可导且三阶导数有界, 期望路径的曲率满足kd≤1/r1min[9], 若牵引车的控制率取为:
| $ \left\{ \begin{array}{l} {u_1} = {u_{1d}}\\ {\omega _1} = {\rm{ }}{\omega _d} + {\rm{ }}\frac{2}{{{k_2}}}[{\rm{ }}2{k_3}{u_{1d}}\cdot{\rm{ }}({\rm{ }}{e_y}{\rm{cos}}\frac{{{e_\theta }}}{2} - {\rm{ }}{e_x}{\rm{sin}}\frac{{{e_\theta }}}{2}){\rm{ }} + \\ \;\;\;\;\;\;\;\;{\rm{sin}}\frac{{{e_\theta }}}{2}] \end{array} \right. $ | (3) |
其中:u1、ω1为牵引车的线速度和角速度; 系数k2, k3 > 0。期望线速度u1d、期望角速度ωd、误差ex、ey、eθ满足式 (4):
| $ \left\{ \begin{array}{l} {u_{1d}} = \sqrt {\dot x_d^2 + \dot y_d^2} \\ {\omega _d}\left( t \right) = \frac{{\ddot y\left( t \right){{\dot x}_d}\left( t \right) - {{\ddot x}_d}\left( t \right){{\dot y}_d}\left( t \right)}}{{{{\dot x}^2}_d\left( t \right) + {{\dot y}^2}_d\left( t \right)}}\\ \left\{ \begin{array}{l} {e_x} = ({x_d} - x){\rm{cos}}\theta + ({y_d} - y){\rm{sin}}\theta \\ {e_y} = - ({x_d} - x){\rm{sin}}\theta + ({y_d} - y){\rm{cos}}\theta \\ {e_\theta } = {\theta _d} - \theta \end{array} \right.\\ {\theta _d} = {\rm{arctan}}\left( {\frac{{{{\dot y}_d}}}{{{{\dot x}_d}}}} \right) + k{\rm{\pi }}\\ k = \left\{ \begin{array}{l} 0.5,\;\;\;\;\;\;{{\dot x}_d} = 0,{{\dot y}_d} \ge 0\\ - 0.5,\;\;\;\;{{\dot x}_d} = 0,{{\dot y}_d} < 0\\ 0,\;\;\;\;\;\;\;\;{{\dot x}_d} > 0\\ 1,\;\;\;\;\;\;\;\;\;\dot x{_d} < 0 \end{array} \right. \end{array} \right. $ | (4) |
则牵引车的运动将渐近收敛到期望路径。
1.2.2 离轴式倒车系统路径跟踪控制方程在实际使用情况中拖挂式机器人系统除了要向前正车完成路径跟踪外, 还希望以向后倒车的方式沿着期望路径将拖车控制到指定位置。若只改变u1d, 沿用正车控制方程, 将会出现拖车与牵引车挤压、碰撞, 甚至倒挂的现象。因此需要重新设计控制方法, 将拖车和牵引车的夹角控制在合理的安全范围内。
把拖车当作“虚拟机器人”, 则倒车运动的控制率为μ2和ω2(分别为拖车的线速度和角速度), 当它们满足定理1的如下条件 (拖车的姿态角θ2初值的取值范围为[-π, π]):
| $ \left\{ \begin{array}{l} {{\bar u}_2} = \bar u{_{2d}} = - \sqrt {\dot x_{2d}^2 + \dot y_{2d}^2} \\ k = \left\{ \begin{array}{l} 0.5,\;\;\;\;\;\;{{\dot x}_{2d}} = 0,{{\dot y}_{2d}} \ge 0\\ - 0.5,\;\;\;\;{{\dot x}_{2d}} = 0,{{\dot y}_{2d}} < 0\\ 0,\;\;\;\;\;\;\;\;{{\dot x}_{2d}} > 0\\ 1,\;\;\;\;\;\;\;\;\;{{\dot x}_{2d}} < 0 \end{array} \right.\\ {{\bar \omega }_2} = {{\bar \omega }_{2d}} + {\rm{ }}\frac{2}{{{k_6}}}[{\rm{ }}2{k_5}{{\bar u}_{2d}}\cdot{\rm{ }}({\rm{ }}{e_{y2}}{\rm{cos}}\frac{{{e_{\theta 2}}}}{2}{\rm{ }} - {\rm{ }}{e_{x2}}{\rm{sin}}\frac{{{e_{\theta 2}}}}{2}{\rm{ }}){\rm{ }} + \\ \;\;\;\;\;\;\;{\rm{sin}}\frac{{{e_{\theta 2}}}}{2}{\rm{ }}] \end{array} \right. $ | (5) |
根据运动学方程可反推得到离轴式倒车系统的控制方程为:
| $ \left\{ \begin{array}{l} {u_1} = {{\bar u}_2}{\rm{cos}}({\theta _1} - {\theta _2}) + \bar \omega {_2}{l_2}{\rm{sin}}({\theta _1} - {\theta _2})\\ {\omega _1} = {{\bar u}_2}\frac{1}{{{c_1}}}{\rm{sin}}({\theta _1} - {\theta _2}) - {{\bar \omega }_2}\frac{{{l_2}}}{{{c_1}}}{\rm{cos}}({\theta _1} - {\theta _2}) \end{array} \right. $ | (6) |
对于连轴式系统, 由于c1=0, 运动学方程显然已经不适用, 根据模型可推得该系统下运动学方程为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {u_1}{\rm{cos}}{\theta _1}\\ {{\dot y}_1} = {u_1}{\rm{sin}}{\theta _1}\\ {{\dot \theta }_1} = {\omega _1}\\ {u_2} = {u_1}{\rm{cos}}({\theta _1} - {\theta _2})\\ {{\dot \theta }_2} = {\rm{ }}\frac{{{u_1}}}{{{l_2}}}{\rm{sin}}({\theta _1} - {\theta _2}) \end{array} \right. $ | (7) |
根据u2=u1 cos (θ1-θ2), 取控制率的u1为:
| $ {u_1} = {{\bar u}_{2d}}{\rm{sec}}({\theta _1} - {\theta _2}) $ | (8) |
则
| $ {\omega _2} = {{\dot \theta }_2} = \bar u{_{2d}}{\rm{tan}}({\theta _1} - {\theta _2})/{l_2} $ | (9) |
使
| $ \left\{ \begin{align} & {{u}_{1}}=~{{{\bar{u}}}_{2d}}~\text{sec}~({{\theta }_{1}}-{{\theta }_{2}}) \\ & {{\omega }_{1}}=\frac{{{{\bar{u}}}_{2d}}}{{{l}_{2}}}~\text{tan}~({{\theta }_{1}}-{{\theta }_{2}})+ \\ & \ \ \ \ \ \ \ l\frac{_{2}({{{\dot{\bar{\omega }}}}_{2}}+~{{{\bar{\omega }}}_{2}})-\text{ }({{{\dot{\bar{u}}}}_{2d}}+~{{{\bar{u}}}_{2d}})\cdot ~\text{tan}~({{\theta }_{1}}-{{\theta }_{2}})}{~{{{\bar{u}}}_{2d}}\text{se}{{\text{c}}^{2}}({{\theta }_{1}}-{{\theta }_{2}})} \\ \end{align} \right. $ | (10) |
RRT算法[11]是一种随机釆样的典型树结构算法, 采用特定的增量方式进行构造, 其基本思想是由控制理论决定随机树的增长方式, 通过在状态空间随机采样状态点将搜索导向空白区域, 逐步缩短随机状态点与树的期望节点即规划目标点间的距离, 从而找到一条连接起始点与目标点的规划路径。这种规划方式抛弃状态空间对障碍物精确定义的要求, 选用碰撞检测函数 (Extend) 来判定系统每个位形与障碍物的关系。这种方式可以简化对空间的建模, 搜索速度快, 不会出现栅格法、人工势场法等算法中易出现的维数灾难问题。因此用于解决复杂环境下复杂系统的路径规划问题[12-13]。
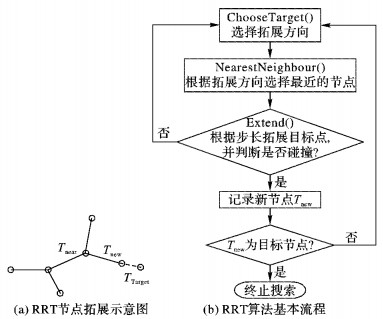
|
图 3 基本RRT算法 Figure 3 Basic RRT method |
基本RRT算法在Extend中采用直线连接的方式拓展新节点, 并根据该直线生成轨迹线进行碰撞检测, 此方法适用于无运动特性约束的单体机器人, 可以提高路径搜索速度。但在拖挂式移动机器人系统中, 由于系统结构复杂, 各个主体 (牵引车和拖车) 运动特性不同, 采用直线拟合轨迹并进行碰撞检测是不切实际的。
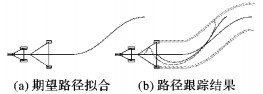
为了合理的将系统运动特性融合入RRT算法中, 并生成合理的路径轨迹, 本文引入样条拟合控制方法, 如图 4所示, 在节点拓展时, 根据Tnear点拖车或牵引车的方位角信息与Tnew点的坐标值, 进行两点间的切向拟合, 形成至Tnew的期望路径, 如图 5(a)所示。根据系统当前工况 (正、倒车、离轴式、连轴式), 选择对应的控制方程 (3)、(6)、(10), 针对期望路径进行路径跟踪, 图 5(b)曲线分别为牵引车后轮、拖车后轮的中点的跟踪轨迹线以及拖车的双轮轨迹线。
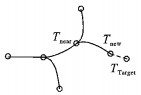
|
图 4 TTMT-RRT节点拓展示意图 Figure 4 Diagram of TTMT-RRT node expansion |
|
图 5 连轴式倒车系统的路径跟踪结果 Figure 5 Path-following result of the connecting-backing system |
牵引车和拖车之间由于几何形状的干涉约束, 往往存在设计最大夹角, 即牵引车与拖车纵向轴的最大夹角 (约50°~90°)。为了在路径规划中考虑夹角安全性问题, 避免倒挂、挤压等问题的出现, 算法添加了夹角约束检测机制, 针对跟踪结果进行最大夹角约束检测, 若满足安全阈值要求, 则进一步进行碰撞检测等; 反之进行重新搜索。
由于在Extend () 时加入了夹角约束条件, 提高了节点拓展的难度, 极易陷入某个局部最优的无限循环中, 即节点树中的某一节点Ti成为随机选择的高概率点, 但由于离环境障碍物过近或者方位角过大, 无法继续拓展, 则会造成算法搜索缓慢甚至搜索失败。为了避免这种情况出现, 就需要在扩展树中删除这种无效点Ti。本文采用节点击中机制, 记录每次拓展所选择的Tnear点以及其击中次数, 选择合理的效率阈值 (亦为节点最大子节点数), 在击中次数超出效率阈值的情况时, 删除Tnear点以及其子树 (子树由于控制约束, 一般无法继承至Tnear的父项)。同时在每次一次拓展失败时, 尝试将Tnear更改为其父节点进行重新拓展。经过测试, 该拓展方法很好地解决局部最优问题, 提高了算法稳定性。
2.2.3 基于贪心思想的结果优化算法由于加入了路径跟踪控制方程, 一般采用上述算法搜索得到的计算结果已经可以直接用于实际操作, 属于可行解, 但不是最优解, 需要对结果路径进行进一步的优化。参考贪心思想, 对节点树主干节点进行优化, 优化方法可分为正向优化与反向优化两种, 此系统采用正向优化方法。
Optimize (T:RRT Tree Points)
1) Pruning (T);
2) New TOpt;
3) TOpt.add (T0, S0);
4) for (int i=0;i < T.st-1;i + +)
5) for (j=T.st-1; j > I)
6) if (Extend (T, Tj, Ti, env)= =TRUE)
7) TOpt.add (Tj); i= j; break;
8) else j--;
9) end for
10) end for
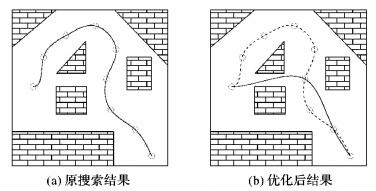
上述算法中, 步骤1) 为对节点树T进行剪枝处理, 留下主干节点 (T0, T1, …, Tn)。步骤2)~10) 为从Ti点和该点系统状态, 依次尝试连接拓展Tn, Tn-1, …, Ti+1, 拓展方法Extend () 参照TTMR Path Planning算法, 直至拓展成功, 若Tj为Tn则结束优化。优化结果如图 6所示。
|
图 6 贪心思想优化算法示意图 Figure 6 Diagram of greedy optimization method |
由贪心思想得到的Ti, 由于改变了Ti点原有的系统状态, 无法保证Tn, Tn-1, …, Ti+1中存在成功拓展点, 若没有则需要进行退回处理, 当Ti退回至T0时必有成功拓展点T1, 因此, 此优化算法是封闭有解的。
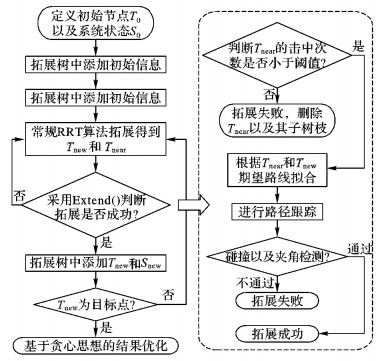
2.2.4 改进算法流程图 7为基于路径跟踪的改进RRT算法流程。
|
图 7 基于路径跟踪的改进RRT算法流程 Figure 7 Improved RRT algorithm flow based on path tracking |
TT MR Path Planning (env: environment, T: RRT Tree Points, Si: System state)
1) Var T0, S0;
2) T.add (T0, S0);
3) TTarget=ChooseTarget ()
4) Tnear=NearestNeighbour (TTarget);
5) Tnew=Calulate (TTarget, Tnear, dl);
6) if (Extend (T, Tnew, Tnear, env)= =TRUE)
7) T.add (Tnew, Snew)
8) if (Tnew= =Tgoal)
9) Optimize (T) and return;
Extend (T, Tnew, Tnear, env) 代码如下:
1) if (HitTimes (Tnear) > n)
2) T.delet (Tnear);
3) return FALSE;
4) el se
5) if (PathTracking (Tnew, Tnear)= =TRUE)
6) if (CollideTest (env)= =FALSE)
7) return TRUE;
8) else return FALSE;
9) else return FALSE;
其中:第1) 行中T0、S0为系统初始状态, 包括牵引车和拖车的初始位置和初始角度 (x10, y10, z10), (x20, y20, z20), 与常规RRT算法不同, TTMR-RRT每个节点记录了系统6个自由度的状态信息。第2)~8) 行为基本RRT算法步骤, 第9) 行为对结果的贪心优化。Extend函数为改进的节点拓展方法, 其中对所选择的Tnear进行击中次数检测, 超出设定的阈值则删减树中的Tnear点以及其子树;否则, 根据样条曲线控制方法拟合期望路径, 计算该曲线的一至三阶导数, 并根据当前拖挂式系统的工况选择合适的路径跟踪控制方程, 进行路径跟踪 (第5) 行), 跟踪的结果满足系统安全夹角要求dθmax=|θ1-θ2} < θrequire, 则进行碰撞检测, 碰撞检测算法一般采用二维面片干涉检查算法, 检测通过则在树上添加新节点。当Tnew为Tgoal, 终止搜索, 对搜索结果进行优化处理 (见图 6), 并根据优化结果进行重新拟合和跟踪。
改进RRT算法可以使搜索结果满足拖挂式移动机器人系统的运动学特性以及安全性要求, 同时, 能保证系统到达目标点的方位角满足需求设定。当系统状态为倒车时, 可精准控制拖车到达目标点的朝向; 当系统状态为正车时, 可控制牵引车到达目标点的朝向。
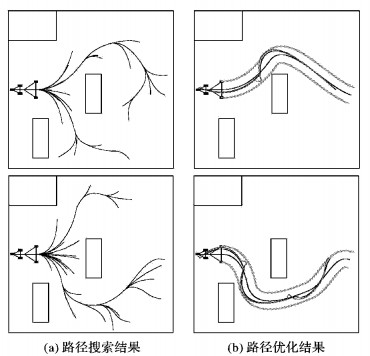
3 实验与分析 3.1 仿真初始信息与典型计算结果根据上述路径跟踪控制方程以及改进RRT算法, 搭建环境模型和系统模型结构, 汇编成软件, 并进行实验验证。以连轴式倒车系统为例, 实验输入数据包括起始点, 起始点朝向A0=180°, 目标点Tgoal(18, 0), 目标点朝向Agoal=160°, 牵引车初始速度u0=-1, 初始角速度ω0=0.6, 系统安全夹角阈值为60°, 搜索步长取为1.5 m, 目标点随机概率取30%, 路径跟踪密度取1 000。典型路径搜索结果如图 8所示。
|
图 8 TTMR-RRT搜索结果 Figure 8 Results of TTMR-RRT method |
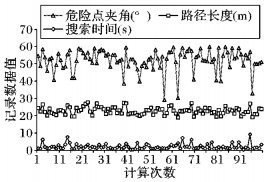
根据当前系统输入参数和环境模型, 进行100次重复计算, 统计结果路径的路径长度、搜索时间以及系统间最大夹角 (见图 9)。
|
图 9 100次仿真计算结果信息 Figure 9 100 simulation results |
图 8(a)为TTMT-RRT搜索得到的节点树状图, 图 8(b)为剪枝以及优化之后的结果。路径行进时间为20.736 s, 牵引车与拖车最大夹角为47.01°, 满足安全阈值60°的要求。由图 8所示, 可行路径主要分为上下两种。
1) 结果切实性。
由图 8可知, 改进算法搜索得到的路径轨迹为连续曲线, 且区分拖车和牵引车各自的运动形态, 存在一定的甩尾现象, 相较原算法的线段式树状图 (图 3(a)) 更贴近实际情况, 因此, 碰撞检测结果也更为准确。
2) 结果稳定性和优化能力。
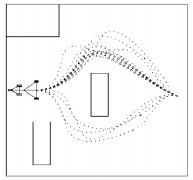
为了验证改进算法的结果稳定性以及时效性, 根据设定的环境和输入信息, 取20次计算结果中拖车双轮中点的轨迹线, 汇总成图 10。由图 10可知, 由于设定的输入信息中标定目标点朝向为160°(偏上), 出现上路结果的概率明显大于下路; 其次, 虽然算法具有一定随机性, 但经过后处理优化后, 路径结果基本趋向稳定。由此可知, 相对于基本RRT算法, 改进算法考虑了终点定位约束, 在结果稳定性上明显优于原算法; 同时, 解决了基本RRT算法存在的绕远问题, 在时效性上更胜一筹。
|
图 10 拖车双轮中点轨迹线20次计算结果汇总图 Figure 10 The 20 trajectory lines of midpoint of trailer's two-wheels |
3) 成功率和安全性。
根据100次仿真结果, 将各结果中系统夹角、路径长度和搜索时间汇总成表 1,成功率为100%。
| 表 1 100次仿真计算统计结果 Table 1 Statistical results of 100 simulations |
由表 1与成功率可知, 相对于未添加节点击中机制情况下的算法搜索成功率 (56.5%), 提高了43.5个百分点, 可见算法解决了陷入局部最优问题,提高了搜索稳定性, 在封闭性和收敛性上是相对成功的; 同时, 系统间最大夹角为59.99°, 未超过设定的安全夹角阈值60°, 因此, 算法在结果安全性上也能够予以保证。
4) 结果时效性。
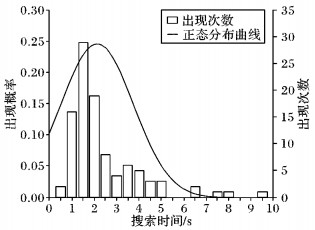
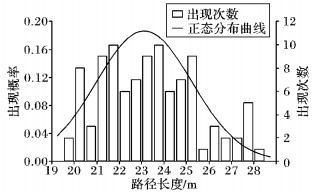
根据统计结果绘制正态分布曲线 (图 11~12), 其中, 路径搜索耗时的标准方差为1.62 s, 路径长度的标准方差为2.13 m。
|
图 11 搜索时间统计结果 Figure 11 Statistical results of searching time |
|
图 12 路径长度统计结果 Figure 12 Statistical results of path length |
由图 12可知, 路径长度分布较为平均, 搜索结果处于在20~25 m中较多, 平均路径长度为22.873 m, 最短路径为19.097 m, 两者相差16.51%, 进一步验证了改了算法在结果时效性上的提高。根据路径长度正态分布曲线可知, 平均只需搜索10次以内, 即可得到最优路径, 结合搜索时间亦可确定此输入状态的系统, 在搜索20 s以内可以得到可行的最优路径。
5) 搜索快速性。
在搜索速度方面, 基本RRT算法在环境变量一致的前提下, 搜索平均耗时在0.78 s, 从统计结果来看, 由于改进算法加入了路径跟踪计算以及夹角约束条件, 牺牲了部分快速性。搜索以及结果优化的平均耗时为2.15 s, 由图 11可知, 结果在2 s以下的占66%, 在1.5 s以下的占47%, 较原算法耗时增加2倍左右, 该时间满足快速设计的需求, 但还不足够用于实时系统, 有一定改进空间。由于搜索耗时和环境复杂度、路径长度、搜索步长、每步长跟踪间隔、电脑性能都有密切关系, 本结果中为了提高结果的精确度, 设定每步长搜索间隔为1/1 000, 若用于实时搜索, 在满足精度的前提下, 可将间隔减低至1/300, 经过验证, 搜索速度将以相同比例提升。
根据上诉仿真算例可知, TTMT-RRT算法在结果稳定性、切实性、成功率、时效性以及安全性上都优于原算法; 反之, 不可避免地在快速性上有所牺牲, 在后续研究中需要进一步优化改进。
4 结语本文针对带一节拖车的拖挂式移动机器人系统, 提出了一种基于路径跟踪技术的自动路径规划算法。该算法融合RRT快速随机数拓展算法, 通过引入样条曲线拟合方法和路径跟踪控制技术, 提高了原算法的精准性; 加入节点击中机制和贪心优化算法优化了算法搜索成功率以及时效性。通过仿真实验分析, 进一步验证了本文算法的正确性和可靠性。
由于加入了诸多约束和计算方程, 算法在搜索耗时上高于基本RRT算法, 牺牲了原有算法搜索速度快的优点, 虽然速度可以通过降低搜索精度的方法予以提高, 但治标不治本, 如何在保证精度的前提下尽可能提高速度将是后续研究的重点。此外, 本文研究的基本对象为带一节拖车的拖挂式移动机器人系统, 理论上可以通过改动路径跟踪控制方程拓展为多节拖车, 在后续研究中, 也将针对多节拖车系统进行进一步研究和验证。
| [1] | MYOUNGKUK P, WOOLIN C, MUNSANG K. Control of a mobile robot with passive multiple trailers[C]//Proceedings of the 2004 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 2004:4369-4374. |
| [2] | 王沛栋. 改进蚁群算法及在路径规划问题的应用研究[D]. 青岛: 中国海洋大学, 2012. ( WANG P D. Research on improved ant colony algorithms and applications for path planning problems[D]. Qingdao: Ocean University of China, 2012. ) |
| [3] | 巩敦卫, 曾现峰, 张勇. 基于改进模拟退火算法的机器人全局路径规划[J]. 系统仿真学报, 2013, 25 (3) : 480-483. ( GONG D W, ZENG X F, ZHANG Y. Global path planning method of robot based on modified simulated annealing algorithm[J]. Journal of System Simulation, 2013, 25 (3) : 480-483. ) |
| [4] | 刘传领. 基于势场法和遗传算法的机器人路径规划技术研究[D]. 南京: 南京理工大学, 2012. ( LIU C L. Researches on technologies for robot path planning based on artificial potential field and genetic algorithm[D]. Nanjing: Nanjing University of Science & Technology, 2012. ) |
| [5] | 杜明博, 梅涛, 陈佳佳, 等. 复杂环境下基于RRT的智能车辆运动规划算法[J]. 机器人, 2015 (4) : 443-450. ( DU M B, MEI D, CHEN J J, et al. RRT-based motion planning algorithm for intelligent vehicle in complex environments[J]. Robot, 2015 (4) : 443-450. ) |
| [6] | LAVALLE S M. Rapidly-exploring random trees: a new tool for path planning[EB/OL].[2016-03-01]. http://msl.cs.illinois.edu/~lavalle/papers/Lav98c.pdf. |
| [7] | 冯林, 贾菁辉. 基于对比优化的RRT路径规划改进算法[J]. 计算机工程与应用, 2011, 47 (3) : 210-213. ( FENG L, JIA J H. Improved algorithm of RRT path planning based on comparison optimization[J]. Computer Engineering and Applications, 2011, 47 (3) : 210-213. ) |
| [8] | 苑晶, 黄亚楼, 孙凤池. 两种连接形式的拖挂式移动机器人路径跟踪控制[J]. 控制理论与应用, 2008, 25 (3) : 398-406. ( YUAN J, HUANG Y L, SUN F C. Path following control for tractor-trailer mobile robots with two kinds of connection forms[J]. Control Theory & Applications, 2008, 25 (3) : 398-406. ) |
| [9] | 徐国华. 带拖车的轮式移动机器人系统的研究[D]. 天津: 南开大学, 1998. ( XU G H. Researches on tractor-trailer mobile robots system[D]. Tianjin: Nankai University, 1998. ) |
| [10] | 刘作军, 孔鑫, 杨鹏, 等. 带拖车移动机器人的运动学分析与仿真[C]//中国控制与决策学术年会文集. 沈阳: 东北大学, 2007: 1309-1316. ( LIU Z J, KONG X, YANG P, et al. Kinematics analyze and simulation for tractor-trailer mobile robot[C]//Proceedings of the 2006 Chinese Control and Decision Conference. Shengyang: Northeastern University, 2007: 1309-1316. ) |
| [11] | LAVALLE S M, KUFFNER J J. Randomized kinodynamic planning[J]. International Journal of Robotics Research, 1999, 20 (5) : 473-479. |
| [12] | 徐娜, 陈雄, 孔庆生, 等. 非完整约束下的机器人运动规划算法[J]. 机器人, 2011, 33 (6) : 666-672. ( XU N, CHEN X, KONG Q S, et al. Motion planning for robot with nonholonomic constraints[J]. Robot, 2011, 33 (6) : 666-672. ) |
| [13] | CHENG P, LAVALLE S M. Reducing RRT metric sensitivity for motion planning with differential constraints[EB/OL].[2016-03-01].http://msl.cs.uiuc.edu/~pcheng1/papers/thesis.ps. |




