差分进化 (Differential Evolution, DE) 算法[1]是基于群体差异的启发式优化算法,其原理简单、受控参数少、鲁棒性强,易于理解和实现[2]。DE算法作为一种简单实用的全局搜索算法,已被证明是求解非线性、不可微和超高维等复杂函数的有效手段[3],在科学研究与实际工程领域都得到了广泛的应用[4]。
类似于其他的进化算法,DE算法也存在着早熟和收敛速度过慢的现象,为了解决这些问题,国内外很多学者对DE算法进行了大量的改进,算法的改进主要聚焦在三个方面,一是对参数的选取机制的研究,如Brest等[5]引入自适应缩放因子 (Factor, F) 和交叉概率 (Crossover Rate, CR),提出一种参数自适应的差分进化算法; 汪慎文等[6]通过改变变异算子的学习方式,提出朴素差分进化算法。二是对差分变异策略的研究,如吕铭晟等[7]将标准差分进化算法的两种变异策略串行组合,提出多变异策略差分进化算法。三是DE与其他具有某种优良特性的策略的集成,如王丛佼等[8]采用DE标准框架,当群体适应值方差小于一定阈值时,引入极值优化算法,提出基于极值优化的混合差分进化算法;匡芳君等[9]设置初始种群为随机双种群,分别采用混沌差分进化算法和混沌粒子群优化算法协同寻优,提出混沌差分进化粒子群协同优化算法;张大斌等[10]在鱼群算法快速收敛的基础上引入差分进化算法,提出基于差分进化的鱼群算法。学者们的改进不同程度地提升了DE的收敛性能,然而DE及其改进算法依然存在收敛精度不高、对不同特征的基准测试函数鲁棒性不好等问题,例如文献[5-8]的算法在病态的Rosenbrock函数上均表现不佳。
本文将混沌分散策略和反向学习机制引入差分进化算法中,设计了一种基于反向学习的跨种群差分进化算法 (Cross-Population Differential Evolution algorithm based on Opposition-based Learning, OLCPDE)。该算法通过混沌分散策略产生初始种群,按适应度值大小将种群划分为精英种群和普通种群,对精英种群采用标准的DE/best/1/bin差分进化策略,对普通种群采用反向学习改进的DE/rand/2/bin差分进化策略;为了增加算法的鲁棒性,提高算法对单峰函数的求解精度和稳定性,同时采用了跨种群的DE/best/1/bin差分进化策略,借助种群间的并行机制和多种策略,以达到提高收敛速度,增强全局搜索能力的目的。通过选取测试函数进行寻优仿真验证了算法具有较高的收敛速度和全局搜索能力。
1 标准差分进化算法DE算法是一种基于实数编码的群体优化算法,与其他进化算法类似,首先需要将种群初始化,然后对种群个体进行交叉、变异和选择操作,通过多次迭代,最终使种群个体趋于全局最优解。差分进化算法的主要操作如下:
1) 种群初始化。令X i(t)=(xi1, xi2, …, xiD) 为第t代种群的第i个个体,根据式 (1) 在可行域内随机产生种群规模为NP,个体分量为D的初始种群X (0)。
| $ \begin{array}{l} {x_{ij}}(0) = x_{ij}^L + {\rm rand}(0,1)(x_{ij}^U - x_{ij}^L);\\ \;\;\;\;\;\;\;\;i = 1,2, \cdots ,NP;j = 1,2, \cdots ,D \end{array} $ | (1) |
其中:xij(0) 表示第0代第i个个体的第j个分量;xijU、xijL分别表示Xi中第j个分量的上下界;rand (0, 1) 表示随机产生[0, 1]区间内的数。
2) 变异操作。变异操作为差分进化算法的核心,从种群中随机选择一个个体X r1,作为待变异个体,再随机选择两个个体X r2,X r3(NP≥4) 作为扰动个体,根据式 (2),将这两个个体的向量差缩放后与待变异个体进行向量合成,得到变异后的个体U i。
| $ \begin{array}{c} {u_{ij}}(t + 1) = {x_{{r_1}}}_j(t) + F \cdot ({x_{{r_2}}}_j(t) - {x_{{r_3}}}_j(t));\\ {r_1} \ne {r_2} \ne {r_3} \end{array} $ | (2) |
其中:F为缩放比例因子,通常取值为[0.5, 1]。
3) 交叉操作。依式 (3),将变异后的个体和当前的演化个体以离散交叉的方式进行交叉操作生成中间个体C i(t+1),以提高种群多样性。
| $ {c_{ij}}(t + 1) = \\ \;\;\;\;\left\{ {\begin{array}{*{20}{l}} {{u_{ij}}(t + 1),\;\;\;{\rm rand}(0,1) \le CR{\rm{ 或 }}j = {\rm rand}(D)}\\ {{x_{ij}}(t),\;\;\;\;\;\;\;\;{\rm{ 其他}}} \end{array}} \right. $ | (3) |
其中:rand (D) 是区间[1, D]的随机整数,CR∈[0, 1]是交叉概率。
4) 选择操作。根据式 (4),对中间个体和当前个体之间进行贪婪选择,通过计算个体目标函数值,将其进行比较,选择适应度大的作为下代种群个体。
| $ {{\boldsymbol{X}}_{{i}}}{{(t + 1)}} = \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{C}}_{{i}}}{{(t + 1)}},\;\;\;{\rm{ }}f({{\boldsymbol{C}}_{{i}}}{{(t + 1)}}) \ge f({{\boldsymbol{X}}_{{i}}}{{(t)}})}\\ {{{\boldsymbol{X}}_{{i}}}{{(t)}},\;\;\;\;\;\;\;\;{\rm{ 其他}}} \end{array}} \right. $ | (4) |
此外,DE算法还有多种差分策略,以上的基本差分算法实质上采用的是DE/rand/1/bin策略,除此之外,还有很多常用和经典的差分策略,如本文后续部分使用到的差分策略是DE/best/1/bin和DE/rand/2/bin,如式 (5) 和式 (6)。
| $ {u_{ij}}(t + 1) = {x_{{\rm{best}}}}_j(t) + F \cdot ({x_{{r_2}}}_j(t){\rm{ - }}{x_{{r_3}}}_j(t));{r_2} \ne {r_3} $ | (5) |
| $ \begin{array}{c} {u_{ij}}(t + 1) = {x_{{r_1}}}_j(t) + F \cdot ({x_{{r_2}}}_j(t) + {x_{{r_3}}}_j(t) - {x_{{r_4}}}_j(t)- \\ {x_{{r_5}}}_j(t));{r_1} \ne {r_2} \ne {r_3} \ne {r_4} \ne {r_5} \end{array} $ | (6) |
DE算法在进化过程中,个体间差异性逐渐变小,种群多样性降低,算法探索能力下降,容易陷入局部最优,出现早熟等问题,为此学者们从不同的角度对算法进行了改进。标准DE算法在寻优过程中的控制参数保持不变,无法较好地满足进化各阶段算法对参数的特殊要求,基于此学者们提出了参数自适应的DE算法;由于初始种群随机产生,初始解的质量无法保证,因此一些学者对初始化进行了改进;差分策略是DE算法的标志性特征,影响着算法收敛速度和寻优精度,因此学者们提出了多种不同的差分进化策略;DE算法的贪婪选择策略在提高算法收敛速度的同时降低了种群的多样性,为避免早熟,学者们改进了选择策略;考虑到单个种群在进化过程中容易丧失多样性,学者们提出了多个子种群进化模式,通过种群间的信息共享和交换,保证算法继续进化。在学习总结学者们的改进策略的基础之上,本文同时对种群初始化、选择策略和单种群进化模式等三个方面进行了改进,提出了基于反向学习的跨种群差分进化算法。
2.1 基于混沌分散策略的种群初始化标准DE算法的初始种群是随机产生的,用这种方式产生的初始种群,可能会使一些种群个体集中在某一区域或者远离最优解,无法保证初始解的质量,因此,限制了算法的求解效率。而混沌是非线性动力学系统中特有的一种现象,具有内在的随机性和遍历性等特点,它能弥补随机产生种群的缺点,提高初始种群的质量,为后续的差分操作找到最优解提供了保证。常用的混沌模型是一维Logistic映射[11],其迭代公式为:
| $ {y_{k + 1}} = \mu {y_k}(1 - {y_k});k = 0,1,2,... $ | (7) |
其中:k为迭代次数,μ为控制系统混沌行为的参数。当μ值确定后,由任意初值y0∈[0, 1], 可以迭代出一个确定的时间序列y1, y2, …, yk。当μ=4时,系统没有稳定解,是[0, 1]区间的满映射,呈现出完全混沌状态。
本文算法初始种群产生的步骤是:随机产生一个分量在区间[0, 1]的D维向量Y 0=(y01, y02, …, y0D),将其代入式 (7),迭代NP-1次,得到混沌向量Y s=(ys1, ys2, …, ysD), s=0, 1, …, NP-1;再将NP个向量的各个分量代入到公式xsj=xsjL+ysj·(xsjU-xsjL), s=0, 1, …, NP-1; j=1, 2, …, D中,得到混沌分散后的初始种群;分别计算这NP个个体的目标函数值,选择最优的
反向学习策略 (Opposition-Based Learning, OBL) 是近年来计算智能领域中出现的一种新技术,已应用到多种优化算法中[12-15]。它的主要思想是:对一个可行解,同时计算并评估其反向解,从中选择较优的解作为下一代种群。反向学习机制通过搜索更多有效区域来提高群体的多样性,增强算法的全局搜索能力。本文将其应用在对普通种群的选择策略上,具体步骤如下:
步骤1 对变异前的普通种群X i(t) 和变异交叉后的中间种群C i(t+1),分别求其反向种群Xi(t)、Ci(t+1),其个体为:
| $ \begin{array}{l} {{{\boldsymbol{\bar X}}}_{{i}}}{{(t)}} = \{ {{\bar x}_{i1}},{{\bar x}_{i2}}, \cdots ,{{\bar x}_{iD}}\} \\ {{{\boldsymbol{\bar C}}}_{{i}}}{{(t + 1)}} = \{ {{\bar c}_{i1}},{{\bar c}_{i2}}, \cdots ,{{\bar c}_{iD}}\} \end{array} $ |
其中:
| $ \begin{array}{l} {{\bar x}_{ij}} = (x_{ij}^U + x_{ij}^L) - {x_{ij}},{{\bar c}_{ij}} = (x_{ij}^U + x_{ij}^L) - {c_{ij}}\\ i = 1,2, \cdots ,NP{\rm{ - }}\left\lceil {NP/2} \right\rceil ;j = 1,2, \cdots ,D \end{array} $ |
步骤2 合并种群X i(t),C i(t+1),Xi(t),Ci(t+1),计算个体的适应度,按适应度值由大到小排序,选取适应度值大的前NP-
将反向学习精英选择策略用于对普通种群变异交叉后进行选择操作,能够有效地提升普通种群进化后的个体的质量,缩小与精英种群个体之间的差距,促进种群之间的交流。反向学习策略通过变换算法的搜索空间,对当前及反向空间进行搜索,使算法避免陷入局部最优,有效提高算法寻优概率[16]。3.3节的实验结果验证了该策略的有效性。
2.3 子种群的并行差分进化策略OLCPDE算法是一种并行的差分进化算法,进化示意图如图 1所示。该算法根据适应度,将种群划分2个子种群:精英种群和普通种群。适应度好的前
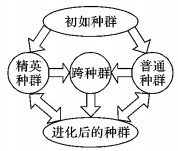
|
图 1 并行进化示意图 Figure 1 Parallel evolution diagram |
为了增加算法的鲁棒性,提高算法的收敛精度和稳定性,以期能获得稳定的最优解,本文提出了一种跨种群的DE/best/1/bin策略进行差分进化。该策略生成种群规模为
步骤1 种群初始化。利用混沌分散种群初始化策略产生规模为NP的初始种群,计算个体适应度,并将其按适应度值大小进行排序,选取前
步骤2 对精英种群采用DE/best/1/bin差分策略进行差分进化,得到个体数为
步骤3 对普通种群采用DE/rand/2/bin差分策略进行变异和交叉,采用2.2节的反向学习精英选择策略进行选择,得到个体数为NP-
步骤4 选取精英种群中的当前最优个体为待变异个体,从普通种群中随机选择两个个体组成扰动向量,采用跨种群的DE/best/1/bin策略进行交叉、变异和选择,得到个体数为
步骤5 将三种策略进化后的NP+
步骤6 判断是否满足算法终止的条件,若当前迭代次数小于最大迭代次数并且没有寻到最优值则转向步骤2,否则转步骤7。
步骤7 结束寻优,输出结果。
3 函数仿真与分析 3.1 测试函数与参数设置为了测试OLCPDE算法的性能,本文选取了12个具有不同特点的基准Benchmark函数进行测试,其中f1至f6为单峰函数,f7至f12为多峰函数,测试函数的特征描述如表 1所示。
| 表 1 测试函数 Table 1 Benchmark functions |
选取4种典型算法与OLCPDE算法进行比较,分别是策略为DE/rand/1/bin和DE/rand/2/bin的标准差分进化算法、被广泛认可的jDE[5]和RMDE[17]。本文选取种群规模NP=80,问题维度n=10。差分进化算法的参数设置主要涉及缩放因子F和交叉概率CR两个参数,OLCPDE、DE/rand/1/bin、DE/rand/2/bin取F=0.5,CR=0.8;jDE的F和CR是自适应的,参照文献[5]的设置;RMDE参照文献[16]的设置F=0.5,CR=0.9,调和参数Mr=0.99。设置f2最大迭代次数设为4 000,f10最大迭代次数为2 000,f11、f12最大迭代次数为1 000,其余的函数最大迭代次数设为300。
3.2 实验结果及分析 3.2.1 算法收敛的性能采用上述5种算法对表 1中12个测试函数进行寻优,每种算法的每个函数独立运行30次,寻优结果见表 2,收敛曲线如图 2所示 (除图 2(g)、(h)、(j)外,其他子图的纵轴均为对数坐标轴)。
| 表 2 OLCPDE与4种经典算法的收敛性能对比 Table 2 Convergence performance comparison between OLCPDE and four classical algorithms |
根据表 2和图 2,对算法性能从收敛速度、求解精度以及稳定性等多角度进行对比分析。
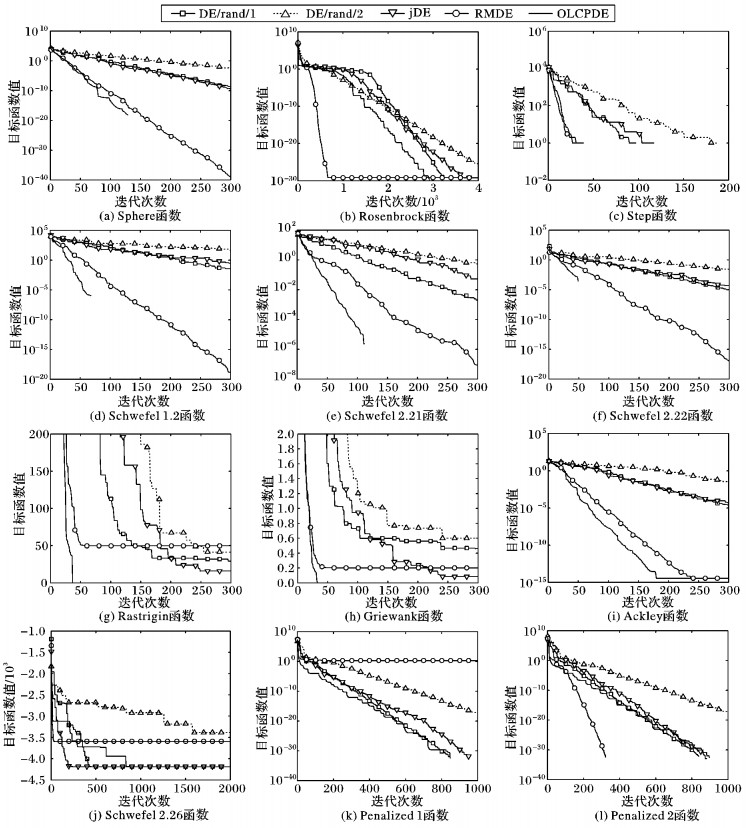
|
图 2 OLCPDE与4种经典算法的收敛曲线 Figure 2 Convergence curves of the OLCPDE and four classical algorithms |
对于f1、f4、f5、f6函数,OLCPDE算法在较少的迭代次数下,能够稳定地收敛到全局最优解,而其他4种算法无论是收敛速度还是求解精度都要差于OLCPDE算法。对于非凸、病态单峰函数f2,OLCPDE算法、DE/rand/1/bin算法、jDE算法和RMDE算法均有可能求解到最优解,但只有前两种算法最稳定。对于步长函数f6,除RMDE算法,其余四种算法均能稳定求解到全局最优解,其中OLCPDE算法的收敛速度最快。综合f1~f6函数的求解结果,在求解单峰函数方面,OLCPDE算法具有较快的收敛速度、较强的全局搜索能力和稳定性。
对于f7、f8、f9函数,OLCPDE算法的收敛速度、求解精度和稳定性都要好于其他算法,虽然在对f9函数求解时发生了1次早熟,但求解的精度仍好于其他4种算法;对于f10、f11、f12函数,OLCPDE算法、DE/rand/1/bin算法和jDE算法表现得十分出色,都能稳定地求解到全局最优解,且这三种算法的求解速度差别不大。综合f7~f12函数的求解结果,求解多峰复杂函数时,OLCPDE算法同样具有较好的收敛速度、求解精度以及鲁棒性。
综上所述,无论单峰函数或多峰函数,OLCPDE算法均可快速获取最优值,实验结果明显优于其他算法,说明OLCPDE算法具有更好的寻优性能。
3.2.2 算法复杂度分析由表 3可以看出,在最大迭代次数相同的情况下,对于f1~f9函数OLCPDE算法的平均耗时最短,DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法次之,RMDE算法的耗时最长。对于f10~f12函数,OLCPDE函数平均耗时大于DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法,约是它们耗时的1.5倍。分析算法可知,DE/rand/1/bin算法、DE/rand/2/bin算法、jDE算法和RMDE算法的时间复杂度相同,均为O(NP*D),其中RMDE算法的过程更为复杂,所以耗时较多。虽然,OLCPDE算法的时间复杂度为O(3NP*D/2),但是由于算法的收敛速度较快,在最大迭代次数之内搜索到全局最优点,停止搜索,因此对f1~f9函数搜索的时间消耗小于其他算法。
| 表 3 OLCPDE与4种经典算法的平均寻优时间 s Table 3 Average optimizing time of OLCPDE and four classical algorithms s |
为了测试反向学习精英选择策略在算法中的有效性,按照对照实验的原则,设置3个参照算法,分别是:普通种群使用1对1贪婪选择的OLCPDE算法 (记作CPDE)、精英种群使用了反向学习精英选择策略的OLCPDE算法 (记作EOLCDE) 和跨种群策略使用反向学习精英选择的OLCPDE算法 (记作COLCDE) 与OLCPDE算法进行比较,参数设置与3.1节相同,寻优结果见表 4。
| 表 4 OLCPDE与3个参照算法的收敛性能和寻到最优值的成功次数对比 Table 4 Comparison of convergence and successful optimization number between OLCPDE and three reference algorithm |
根据表 4可以看出,对于上述12种函数,除了f3函数,不使用反向学习精英选择策略的CPDE算法均无法快速稳定地收敛到全局最优点,说明了使用反向学习精英选择策略能有效加快算法的收敛;将反向学习精英选择策略分别用于对精英种群和对跨种群进行选择的EOLCDE算法和COLCDE算法,能够寻找到一部分函数的最优值,但是对于其他函数,则容易陷入局部最优。因此,引入反向学习精英选择策略能够提高算法的收敛精度和速度,将反向学习精英选择用作普通种群的选择策略,才能够最有效地提升算法的全局寻优能力。
3.3.2 跨种群策略对函数寻优的有效性分析为了测试跨种群策略在算法中的有效性,设置了取消跨种群策略的OLCPDE算法 (记作OLDE) 与OLCPDE算法分别对6个单峰函数和6个多峰函数进行对比测试,参数设置与3.1节相同,寻找到最优解的次数统计结果见表 5。
| 表 5 OLCPDE与OLDE对单峰和多峰函数寻优成功次数比较 Table 5 Comparison of successful optimization number between OLCPDE and OLDE for one-peak functions and multi-peak functions |
根据表 5可以看出虽然跨种群策略对多峰函数的寻优的影响性不显著,但是它能有效提升单峰函数寻优的成功次数,使用跨种群策略的OLCPDE算法能够防止单峰函数早熟,增加算法的稳定性。
3.4 OLCPDE算法分析根据上述图表可以看出,除个别多峰函数外,OLCPDE算法均能够稳定地收敛到全局最优解。通过对本文算法策略性能的进行分析,结论如下:
1) 通过对反向学习精英选择策略的性能进行分析,证明该策略有效提升DE算法的寻优精度;同时,将该策略用于普通种群,能最大限度地提高算法的寻优精度,大幅提升寻到最优解的概率。若取消该策略,使用标准DE算法的选择策略,除个别单峰函数,均无法达到最优解。
2) 通过分析跨种群策略对算法的影响,证明运用该策略能有效提升单峰函数寻优成功的次数,进一步提升算法寻优的稳定性。
3) 本文算法采用多个子种群进化模式,提高种群多样性,有效弥补单种群进化过程中种群多样性不足的缺陷,防止算法早熟。
综上所述,本文算法策略的使用能有效提升算法性能,无论单峰函数还是多峰函数,OLCPDE算法均能高效、稳定地寻到最优解。
4 结语针对差分进化算法寻优精度低、收敛速度慢等缺陷,本文提出了一种基于反向学习的跨种群差分进化算法 (OLCPDE),引入混沌分散策略来种群初始化能有效提升初始种群的质量,对普通子种群应用反向学习精英选择策略,扩大种群的搜索范围,提升算法的全局搜索能力,采用跨种群的差分进化策略,进一步增强了算法寻优的稳定性。通过对12个标准测试函数的实验,说明了OLCPDE算法能有效地避免早熟,具有较好的收敛速度、优化精度和鲁棒性。将改进的算法应用到实际的工程中,进一步检验算法的性能,是下一步将要研究的内容。
| [1] | STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11 (4) : 341-359. doi: 10.1023/A:1008202821328 |
| [2] | VESTERSTROM J, THOMSEN R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems[C]//Proceedings of the 2004 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2004:267-282. |
| [3] | PRICE K, STORN R M, LAMPINEN J A. Differential evolution: a practical approach to global optimization (natural computing series)[J]. Natural Computing, 2005, 141 (2) : 1-24. |
| [4] | VARADARAJAN M, SWARUP K S. Network loss minimization with voltage security using differential evolution[J]. Electric Power Systems Research, 2008, 78 (5) : 815-823. doi: 10.1016/j.epsr.2007.06.005 |
| [5] | BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10 (6) : 646-657. doi: 10.1109/TEVC.2006.872133 |
| [6] | 汪慎文, 张文生, 秦进, 等. 朴素差分进化算法[J]. 计算机应用, 2015, 35 (5) : 1333-1335. ( WANG S W, ZHANG W S, QIN J, et al. Naive differential evolution algorithm[J]. Journal of Computer Applications, 2015, 35 (5) : 1333-1335. ) |
| [7] | 吕铭晟, 沈洪远, 李志高, 等. 多变异策略差分进化算法的研究与应用[J]. 计算机工程, 2014, 40 (12) : 146-150. ( LYU M S, SHEN H Y, LI Z G, et al. Research and application of differential evolution algorithm under multiple mutation strategy[J]. Computer Engineering, 2014, 40 (12) : 146-150. ) |
| [8] | 王丛佼, 王锡淮, 肖建梅. 基于极值优化的混合差分进化算法[J]. 计算机科学, 2013, 40 (5) : 257-260. ( WANG C J, WANG X H, XIAO J M. Hybrid differential evolutionary algorithm based on extremal optimization[J]. Computer Science, 2013, 40 (5) : 257-260. ) |
| [9] | 匡芳君, 张思扬, 金忠, 等. 混沌差分进化粒子群协同优化算法[J]. 微电子学与计算机, 2014, 31 (8) : 29-33. ( KUANG F J, ZHANG S Y, JIN Z, et al. Chaotic differential evolution particle swarm cooperative optimization algorithm[J]. Microelectronics & Computer, 2014, 31 (8) : 29-33. ) |
| [10] | 张大斌, 杨添柔, 温梅, 等. 基于差分进化的鱼群算法及其函数优化应用[J]. 计算机工程, 2013, 39 (5) : 18-22. ( ZHANG D B, YANG T R, WEN M, et al. Fish warm algorithm based on differential evolution and its function optimization application[J]. Computer Engineering, 2013, 39 (5) : 18-22. ) |
| [11] | OU C M. Design of block ciphers by simple chaotic functions[J]. IEEE Computational Intelligence Magazine, 2008, 3 (2) : 54-59. doi: 10.1109/MCI.2008.919074 |
| [12] | 周新宇, 吴志健, 王晖. 一种精英反向学习的差分演化算法[J]. 小型微型计算机系统, 2013, 34 (9) : 1647-1652. ( ZHOU X Y, WU Z J, WANG H. A differential evolution algorithm using elite opposition-based learning[J]. Journal of Chinese Computer Systems, 2013, 34 (9) : 1647-1652. ) |
| [13] | WANG H, WU Z, RAHNAMAYAN S. Enhanced opposition-based differential evolution for solving high-dimensional continuous optimization problems[J]. Soft Computing, 2011, 15 (11) : 2127-2140. doi: 10.1007/s00500-010-0642-7 |
| [14] | WANG H, WU Z, RAHNAMAYAN S, et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences, 2011, 181 (20) : 4699-4714. doi: 10.1016/j.ins.2011.03.016 |
| [15] | AHANDANI M A, ALAVI-RAD H. Opposition-based learning in the shuffled differential evolution algorithm[J]. Soft Computing, 2012, 16 (8) : 1303-1337. doi: 10.1007/s00500-012-0813-9 |
| [16] | 董小刚, 邓长寿, 谭毓澄, 等. 求解大规模优化问题的正交反向混合差分进化算法[J]. 计算机应用研究, 2016, 33 (6) : 1656-1661. ( DONG X G, DENG C S, TAN Y C, et al. Hybridization differential evolution algorithm of orthogonal crossover and opposition-based learning for large-scale optimization problem[J]. Application Research of Computers, 2016, 33 (6) : 1656-1661. ) |
| [17] | 欧阳海滨, 高立群, 孔祥勇. 随机变异差分进化算法[J]. 东北大学学报 (自然科学版), 2013, 34 (3) : 330-334. ( OUYANG H B, GAO L Q, KONG X Y. Random mutation differential evolution algorithm[J]. Journal of Northeastern University (Natural Science), 2013, 34 (3) : 330-334. ) |




