在实际生产生活中,许多工程设计与求解的问题可被看作函数优化问题,这类问题具有多目标、非线性、维度高等特点,而且每个目标间通常会发生冲突,而传统优化算法无法很好解决这些矛盾。20世纪后期,人们从蚂蚁、鸟类等群居生物的自组织行为中受到启发,提出诸多新型元启发式算法,如粒子群算法[1]、蝙蝠算法[2]等,成为处理多目标优化问题的向导。
由于布谷鸟搜索 (Cuckoo Search, CS) 算法[3]参数少、便于实现,具有较高的前瞻性,现已经成功应用于工程设计、背包问题等领域并得到广泛关注[4-7]。鉴于它的简单实用,2011年Yang等[8]在CS算法基础上提出了多目标布谷鸟搜索算法 (Cuckoo Search algorithm for Multi-objective Optimization, MOCS) 用于解决多目标优化问题,并把它与结构设计问题相结合;2012年,Chankraskaran等[9]提出基于混沌理论的多目标布谷鸟搜索算法,提高了收敛速度与精度;2013年,Layeb等[10]将MOCS应用到背包问题;2015年,贺兴时等[11]提出基于小生境技术的逐步档案缩减法,并设计了多目标布谷鸟搜索算法,对解的均匀性改善很明显,但求解精度不高;2015年,杨辉华等[12]对莱维飞行的步长控制量等进行改进,提出一种改进布谷鸟搜索算法 (Improved MOCS, IMOCS),其求解稳定性有待加强。
MOCS算法是目前最前沿的元启发式算法,但同其他群智能算法一样[13-16],存在后期搜索速度慢、精度不高、容易陷入局部最优等缺点,在迭代后期受自身寻优机制限制存在诸多不足。为解决上述问题,提出结合混沌云模型的改进多目标布谷鸟搜索算法 (MOCS based on Chaos Cloud Model,CCMMOCS)。通过5个经典多目标函数对其有效性进行检验,结果表明CCMMOCS在解的多样性、均匀性上都比MOCS、多目标粒子群算法 (Particle Swarm Optimization algorithm for Multi-objective Optimization, MOPSO) 等要好。
1 算法MOCSMOCS是一种新颖的群智能算法, 它的思想主要表现在两点:对布谷鸟寄生育雏行为和鸟类或果蝇飞行模式的模拟。
布谷鸟以它特有的寄生育雏而闻名,繁殖后代的时候把卵产在别的鸟巢中,让别的鸟类为其孵化。当这种鸟类发现这些外来蛋时,会选择丢弃外来蛋或放弃自己的巢,在其他地方重筑新巢。根据这种策略,在布谷鸟更新位置时采用了莱维飞行方式。根据上述特点,CS算法中有以下三条规则:
1) 布谷鸟每次只产一个蛋,随后把蛋送到任意选择的一个鸟巢中;
2) 优质的巢里会有优质的蛋,则后代能够更好地繁殖下去;
3) 可供选择的寄主巢穴的数量有限,而且寄主也会发现这些外来蛋,概率为pa,寄主可能也会扔掉这些蛋,或者直接放弃本身的巢去建一个新巢。
在上述基本准则的前提下,采用莱维飞行及随机游动替换鸟巢位置,由以下公式来表述:
| $ X_i^{t + 1} = X_i^t + \alpha \oplus {\rm Levy}\left( \lambda \right) $ | (1) |
其中:α > 0是一个步长,多数情况下α=O(1);⊕表示被选择的目标;λ由莱维分布中的最大步长决定;Xig是第g代第i维的随机解。
针对p维多目标优化问题,把上述准则进行修改,就能满足p个目标的需求。
1) 一只布谷鸟一次产一个蛋,再把这些蛋丢到任意巢中,第p个蛋代表第p个目标;
2) 任意巢里的蛋都会以pa的概率被丢掉,有p个蛋的一个巢根据蛋的相似性和区别按相同概率被重建。
第一条准则是随机过程,第二条准则的修改近似看作变异策略,这样就使得单目标优化算法修改后为多目标所用。
2 混沌理论和云模型 2.1 混沌理论混沌理论[17]针对全局优化问题而言,是变量从混沌空间与解空间的转换模型,混沌变量对初值敏感,具有遍历性、随机性和规律性。作为优化设计方向通用的优化方式,混沌理论能很好避免其他算法易陷入局部收敛的问题。根据上述特点,把它应用在全局优化搜索中。Logistic映射是典型的混沌系统,可以用混沌序列对部分布谷鸟个体进行混沌扰动:
| $ {x_{i + 1}} = u{x_i}\left( {1 - {x_i}} \right),i = 0,1,...,N $ | (2) |
其中:u为控制变量,u∈(2, 4],当u=4时,Logistic完全处于混沌状态;x0∈(0, 1) 为混沌变量的初始值。
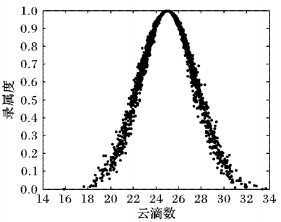
2.2 云模型云模型是由李德毅院士等[18]提出,将定性知识和定性概念与其定量数值表示之间相互转换的有力手段,用于表述日常生活中的不确定概念,是定性定量结合的事物处理不确定模型。正态云模型有三个特征:期望Ex、熵En和超熵He。Ex是定性概念的最高点,隶属度为1,是论域中心值。En与度量范围密切相关,熵值的多少与定性概念被度量范围成正比,同时能反映定性概念中云滴出现的不确定性,体现模糊性和不确定性的关系,熵越小,确定性量化就更精确。He是熵的熵,是云模型云滴离散程度的标志,云图中体现云的“厚度”,He越大则云越厚,隶属度的不确定性及离散度也越大。图 1为Ex=25,En=2.5,He=0.2,云滴数n为2 000的云图。
|
图 1 Ex=25,En=2.5,He=0.2的云图 Figure 1 Cloud for Ex=25, En=2.5, He=0.2 |
在MOCS中,采用随机初始化产生初始鸟巢位置,具有较大的盲目性,解的质量不高;而仅采用莱维飞行搜索机制更新鸟巢位置,在迭代后期收敛速度及精度无法满足优化需求。为解决上述问题,结合混沌云模型来改进MOCS。寻优时,如果当前目标函数的适应度值较大即表示与Pareto真实前沿距离较近,应当缩小范围寻优来提高收敛速度;如果适应度值较小表示与Pareto真实前沿距远,应当扩大搜索范围,提高多样性及均匀性,防止发生局部收敛。基本多目标布谷鸟算法寻优后,位置较差的布谷鸟群利用混沌理论来局部寻优,位置较好的布谷鸟群用云模型来再次全局寻优,二者寻优结果产生的最优解替代之前的位置,使算法有效进行全局搜索,避免陷入局部最优。位置的好坏则利用布谷鸟当前位置和平均的适应度值favg比较来得出,如果当前布谷鸟巢适应度值小于favg,即为位置较好;反之,如果当前布谷鸟巢适应度值大于favg,则位置较差。利用正态云发生器[19]的随机性与稳定倾向性的优点,在优化时满足传统的优势同时提高寻优速度,并保持了前沿的均匀性和多样性。其中,Ex为位置较好的布谷鸟巢个体xi,为缩小搜索范围并提高算法稳定性,选取En=2xi, He=En/5。
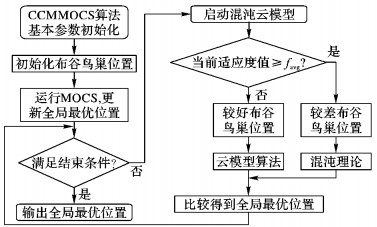
图 2为算法CCMMOCS流程。
|
图 2 算法CCMMOCS流程 Figure 2 Flow chart of CCMMOCS |
算法CCMMOCS的步骤为:
步骤1 初始化。初始化MOCS维数m,鸟窝数量n,被其他鸟类发现并抛弃的概率pa,迭代次数N_iter等。
步骤2 布谷鸟巢位置初始化。随机初始化布谷鸟巢位置。
步骤3 运行MOCS。种群中的每个布谷鸟巢位置执行MOCS, 如果满足结束条件,跳出循环; 否则转步骤4。
步骤4 布谷鸟位置优劣比较。不满足结束条件,启动混沌云模型,比较当前个体布谷鸟巢适应度和平均适应度值favg,分出位置较差的布谷鸟巢和位置较好的布谷鸟巢。
步骤5 混沌理论优化。位置较差的布谷鸟巢利用混沌理论优化。用式 (2) 对位置较差的布谷鸟巢进行Logistic映射产生新个体,产生更优解则取代原位置。
步骤6 云模型优化。位置较好的布谷鸟巢使用云模型来优化。把位置较好的布谷鸟巢个体作为n维正态云云发生器的输入,产生新的布谷鸟个体位置。如果为更优位置,更新最优值。
步骤7 替换最优值。比较云模型和混沌理论分别寻优的值,选出最优值。
步骤8 终止条件。如果满足结束条件,转向步骤9;若不满足,N_iter=N_iter+1,返回步骤4。
步骤9 结束算法,输出最优结果。
4 实验结果 4.1 实验设计为了观察混合算法求解多维优化问题的性能,选择测试环境为: 32位处理器Windows 7,Matlab 2012a。以下是5个标准的多目标测试函数。
1) 测试函数SCH:
| $ {f_1}(x) = {x^2},{f_2}(x) = {\left( {x - 2} \right)^2}, - {10^3} \le x \le {10^3} $ | (3) |
Pareto前沿曲线为凸形,理想Pareto曲线为f2=
2) 测试函数ZDT1:
| $ {f_1}(x) = {x_1},{f_2}(x) = g(1 - \sqrt {{f_1}/g} ) $ | (4) |
| $ g = 1 + \frac{{9}}{{d - 1}}\sum\limits_{i = 2}^d {{x_i}} ;{x_1} \in \left[ {0,1} \right],i = 1,...30 $ | (5) |
其中:d是维数。Pareto前沿曲线为凸形,g=1时为理想Pareto曲线。以下ZDT2、ZDT3中的g与ZDT1中的相同。
3) 测试函数ZDT2:
| $ {f_1}(x) = {x_1},{f_2}(x) = g{(1 - \frac{{{f_1}}}{g})^2} $ | (6) |
ZDT2函数的Pareto前沿曲线为凹形,g=1时为理想Pareto曲线。
4) 测试函数ZDT3:
| $ {f_1}(x) = {x_1},{f_2}(x) = g\left[ {1 - \sqrt {\frac{{{f_1}}}{g} - \frac{{{f_1}}}{g}\sin (10\pi {f_1})} } \right] $ | (7) |
Pareto前沿曲线是分段的,在测试函数ZDT3中,f1的范围为0到0.852,f2的范围为-0.773到1。
5) 测试函数LZ:
| $ {f_1}(x) = {x_1} + \frac{2}{{\left| {{J_1}} \right|}}{\sum\limits_{j \in {J_1}} {\left[ {{x_j} - \sin \left( {6\pi {x_1} + \frac{{j\pi }}{d}} \right)} \right]} ^2} $ | (8) |
| $ {f_2}(x) = 1 - \sqrt {{x_1}} + \frac{2}{{\left| {{J_2}} \right|}}{\sum\limits_{j \in {J_2}} {\left[ {{x_j} - \sin \left( {6\pi {x_1} + \frac{{j\pi }}{d}} \right)} \right]} ^2} $ | (9) |
其中:J1={j|j为奇数且2≤j≤d},J2={j|j为偶数且2≤j≤d}。Pareto前沿曲线为凸状,当xj=sin (6πx1+jπ/d), j=2, 3, …, d, x1∈[0, 1]。LZ的理想Pareto曲线为f2=1-
为验证CCMMOCS的性能,仿真的评价指标主要有两个:两个函数分布之间的误差估计或广义距离 (Generalized Distance, GD) 及测得曲线的多样性Δ。
根据文献[6],定义误差表达式为:
| $ {E_f} = {\left\| {{P^{\rm e}} - {P^{\rm t}}} \right\|^2} = \sum\limits_{j = 1}^N {{{\left( {P_j^{\rm e} - {P^{\rm t}}} \right)}^2}} $ | (10) |
其中:Pe、Pt分别代表所求前沿和理想Pareto前沿。不难发现Ef越接近于0,改进越有效,越接近真实Pareto前沿。
根据文献[10], GD是另一种用来表示所求Pareto与理想Pareto前沿趋近程度指标,GD小,则求得的Pareto与理想Pareto差距小。GD的表达式如下:
| $ GD=\frac{1}{\left| {{P}^{\rm e}} \right|}{{\left( \sum\limits_{i=1}^{\left| {{P}^{\rm e}} \right|}{d_{i}^{2}} \right)}^\frac{1}{2}} $ | (11) |
其中:di为第i个布谷鸟巢与对应理想Pareto前沿的欧氏距离。
Δ是算法多样性的指标,其表达式为:
| $ {\mathit \Delta} = \frac{1}{{(d_1^{\rm e} + d_2^{\rm e}) + \left| {{P^{\rm e}}} \right|\overline d }}\left( {(d_1^{\rm e} + d_2^{\rm e}) + \sum\limits_{i = 1}^{\left| {{P^{\rm e}}} \right| - 1} {\left| {{d_i} - \overline d } \right|} } \right) $ | (12) |
其中:d为d1、d2的平均值,d1e、d2e为在两个目标上所求前沿与对应理想Pareto前沿的极值解之间的距离。Δ同时考虑到多样性及均匀性,d1e、d2e体现分布广度,|di-d|体现分布均匀性。对于理想Pareto前沿,|di-d | =0,d1e=d2e=0。因此,Δ值越接近于0,算法的多样性及均匀性越好。
4.3 实验结果分析在改进程度方面,固定精度Tol=0.25,对迭代次数为500和1 000的CCMMOCS误差进行对比, 结果如表 1所示。
| 表 1 固定精度Tol=0.25时的误差估计Ef Table 1 Estimated error Ef at fixed accuracy Tol=0.25 |
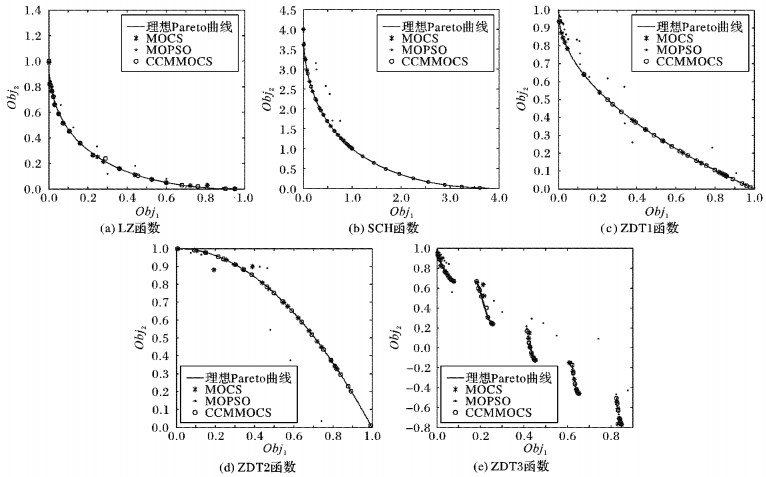
在不同算法的优劣对比方面,选取近年来使用最广泛的MOPSO,设置种群数为30,分别对不同维数的5个常用多目标测试函数进行仿真测试,最大迭代次数为1 000,混沌扰动半径比例系数0.5,独立运行10次。Matlab仿真结果显示在图 3中。由图 3可看出:MOPSO在求解多目标优化问题上精度不高,并且与理想Pareto曲线偏差较大,而CCMMOCS性能则远远优于MOPSO。通过对比标准MOCS,由于云模型的引入更利于全局优化,避免了落入局部收敛,可以明显看出LZ函数及SCH函数 (见图 3(a)和(b)) 更接近理想Pareto曲线,同时在均匀性和多样性上也比标准MOCS要好;图 3(c)中,标准MOCS所得各点分布不均匀,而改进的CCMMOCS波动却很小;对于ZDT2函数 (见图 3(d)),MOCS在搜索后期落入局部最优,而CCMMOCS分布均匀,改进效果也十分明显;图 3(e)为ZDT3函数,改进后的算法在收敛精度上优于原有算法,但由于ZDT3函数前沿是分段的,改进后的算法在寻优过程中的分布相对其他几个函数效果不甚明显。
|
图 3 测试函数的Pareto前沿 Figure 3 Pareto fronts of test functions |
各算法所求GD的均值及方差以及Δ的均值及方差如表 2~3所示。由表可以看出,CCMMOCS的GD及Δ均更接近于0,说明算法的改进是有明显效果的。
| 表 2 MOCS、CCMMOCS、MOPSO所求GD的均值及方差 Table 2 Mean and variance of GD under MOCS, CCMMOC and MOPSO |
| 表 3 MOCS、CCMMOCS及MOPSO所求Δ的均值及方差 Table 3 Mean and variance of diversity under MOCS, CCMMOCS and MOPSO |
表 4中选取了文献中一些可用的结果,将其他算法与改进的CCMMOCS作了对比,可以看出,在相同迭代次数和种群数条件下,CCMMOCS在五个测试函数的优化中具有明显优势,精度比其他算法高出4到5个数量级,改进效果良好。
| 表 4 不同算法的性能评价指标 (n=50, N_iter=500) Table 4 Performance evaluation index of different algorithms (n=50, N_iter=500) |
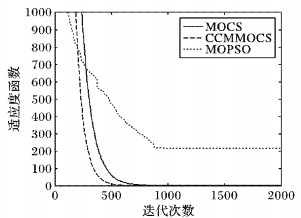
在算法复杂度方面,图 4以SCH函数为例,固定迭代次数为1 000时,CCMMOCS收敛所需次数明显比MOPSO要少,比MOCS也有一定优势,减少了迭代次数,有一定的实用和推广价值。
|
图 4 测试函数SCH在不同算法中的收敛曲线对比 Figure 4 Convergence curve comparison of SCH in different algorithms |
在MOCS进化机制的基础上,利用云模型稳定性与随机性并存的优点和混沌算法随机遍历的特性,提出结合混沌云多目标布谷鸟搜索算法,显著增强了算法均衡全局和局部的搜索能力。实验对比分析说明,CCMMOCS在求解精度、收敛速度和寻找全局最优上都要优于MOCS和文献算法,Pareto前沿曲线更均匀,多样性也有提高。但是云模型和混沌理论在一定程度上对算法的复杂度有影响,研究算法各参数与算法性能的联系,并且将算法更好地应用于生产生活中是下一步需要研究的内容。
| [1] | KENNEDY J, EBERHART R C. Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ: IEEE, 1995: 1942-1948. |
| [2] | YANG X-S. A new metaheuristic bat-inspired algorithm[C]//NICSO 2010: Proceedings of the 2010 Nature Inspired Cooperative Strategies for Optimization, SSCI 284. Berlin: Springer-Verlag, 2010: 65-74. |
| [3] | YANG X-S, DEB S. Cuckoo search via Levy flights[J/OL]. Mathematics, 2010:210-214[2016-05-10]. http://www.oalib.com/paper/3945721#.WNx4OuzNtH4. |
| [4] | YANG X-S, DEB S. Engineering optimization by cuckoo search[J]. International Journal Math Modeling & Numerical Optimization, 2010, 1 (4) : 330-343. |
| [5] | 李志平, 王勇, 张呈志, 等. 云模型的布谷鸟搜索算法[J]. 计算机应用研究, 2016, 33 (1) : 92-98. ( LI Z P, WANG Y, ZHANG C Z, et al. Cloud model cuckoo search algorithm[J]. Application Research of Computers, 2016, 33 (1) : 92-98. ) |
| [6] | 张永韡, 汪镭, 吴启迪. 动态适应布谷鸟搜索算法[J]. 控制与决策, 2014, 29 (4) : 617-622. ( ZHANG Y W, WANG L, WU Q D. Dynamic adaptation cuckoo search algorithm[J]. Control and Decision, 2014, 29 (4) : 617-622. ) |
| [7] | 李煜, 马良. 新型元启发式布谷鸟搜索算法[J]. 系统工程, 2012, 30 (8) : 64-69. ( LI Y, MA L. A New metaheuristic cuckoo search algorithm[J]. Systems Engineering, 2012, 30 (8) : 64-69. ) |
| [8] | YANG X S, DEB S. Multi-objective cuckoo search for design optimization[J]. Computers & Operations Research, 2011, 40 (6) : 1616-1624. |
| [9] | CHANDRASKARAN K, SIMON S-P. Multi-objective scheduling problem: hybrid approach using fuzzy assisted cuckoo search algorithm[J]. Swarm and Evolutionary Computation, 2012, 5 (1) : 1-16. |
| [10] | LAYEB A, LAHOUESNA N, KIRECHE B. A multi-objective binary cuckoo search for bacteria knapsack problem[J]. International Journal of Information Engineering & Electronic Business, 2013, 5 (4) : 8-15. |
| [11] | 贺兴时, 李娜, 杨新社, 等. 多目标布谷鸟搜索算法[J]. 系统仿真学报, 2015, 27 (4) : 731-738. ( HE X S, LI N, YANG X S, et al. Multi-objective cuckoo search algorithm[J]. Journal of Simulation, 2015, 27 (4) : 731-738. ) |
| [12] | 杨辉华, 谢谱模, 张晓凤, 等. 求解多目标优化问题的改进布谷鸟搜索算法[J]. 浙江大学学报 (工学版), 2015, 49 (8) : 1900-1909. ( YANG H H, XIE P M, ZHANG X F, et al. Improved cuckoo search algorithm for multi-objective optimization problems[J]. Journal of Zhejiang University (Engineering Science), 2015, 49 (8) : 1900-1909. ) |
| [13] | ERFANI T, UTYUZHNIKOV S. Directed search domain: a method for even generation of Pareto frontier in multi-objective optimization[J]. Engineering Optimization, 2011, 43 (5) : 467-484. doi: 10.1080/0305215X.2010.497185 |
| [14] | 曾劲涛, 李金忠, 唐卫东, 等. 多目标微粒群优化算法及其应用研究进展[J]. 计算机应用研究, 2011, 28 (4) : 1225-1231. ( ZENG J T, LI J Z, TANG W D, et al. Multi-objective particle swarm optimization algorithm and its application[J]. Application Research of Computers, 2011, 28 (4) : 1225-1231. ) |
| [15] | 郑友莲, 樊俊青. 多目标粒子群优化算法的研究[J]. 湖北大学学报 (自然科学版), 2008, 30 (4) : 351-356. ( ZHENG Y L, FAN J Q. Study on multi-objective particle swarm optimizations algorithm[J]. Journal of Hubei University (Natural Science), 2008, 30 (4) : 351-356. ) |
| [16] | YAHYA M, SAKA M-P. Construction site layout using multi-objective artificial bee colony algorithm with Levy flights[J]. Automation in Construction, 2014, 38 : 14-29. doi: 10.1016/j.autcon.2013.11.001 |
| [17] | DONG S-F, DONG Z-C, MA J-J. Improved PSO algorithm based chaos theory and its application to design flood hydrograph[J]. Water Science and Engineering, 2010, 3 (2) : 156-165. |
| [18] | 李德毅, 刘常昱. 论正态云模型的普适性[J]. 中国工程科学, 2004, 6 (8) : 28-33. ( LI D Y, LIU C Y. Study on the universality of the normal cloud model[J]. Engineering Science, 2004, 6 (8) : 28-33. ) |
| [19] | 付斌, 李道国, 王慕快. 云模型研究的回顾与展望[J]. 计算机应用研究, 2011, 28 (2) : 420-426. ( FU B, LI D G, WANG M K. Review and prospection research of cloud model[J]. Application Research of Computers, 2011, 28 (2) : 420-426. ) |




