子空间降维是机器学习和模式识别的一种常用方法,也是数据挖掘等领域的研究热点。1999年,Lee等[1]在《Nature》上首次提出了非负矩阵分解 (Non-negative Matrix Factorization, NMF) 的概念,通过添加“矩阵中所有元素均非负”的限制条件,保证了分解结果的可解释性。随后,大量改进算法被提出并应用。文献[2]在分解原始矩阵时,对基矩阵和系数矩阵施加稀疏约束,将稀疏编码的思想引入到非负矩阵分解中,提出稀疏约束非负矩阵分解算法 (NMF with Sparseness Constraints, NMFSC) 具有存储空间少的优点; 文献[3]将增量学习与非负矩阵分解相结合,提出了增量非负矩阵分解 (Incremental NMF, INMF) 算法,利用上一步的分解结果参与迭代运算,当再新加入训练样本时不会再重新进行运算,从而节省了运算时间; 文献[4]将稀疏约束和增量学习思想引入到了非负矩阵分解中,提出了稀疏约束下非负矩阵分解 (Incremental NMFSC, INMFSC) 的增量学习算法,在运算时间和稀疏度等指标上都有大幅优化。
上述的标准NMF及其改进算法都属于无监督分解方法,没有考虑样本的标签信息。文献[5]提出一种受限的非负矩阵分解 (Constrained NMF, CNMF) 算法,它充分考虑已有的类别信息,将样本的类别信息作为一个硬约束,使已标记样本类别信息在低维空间中仍保持一致,但该模型没有考虑到数据的几何结构关系。文献[6]将流形学习与非负矩阵分解相结合,提出的图正则化非负矩阵分解 (Graph Regularized NMF, GNMF) 能够在NMF的低维表示中考虑原始样本的近邻结构,使得原始样本的近邻结构在非负矩阵分解的低维中得到很好的保留。
文献[7]提出的稀疏约束图正则非负矩阵分解 (GNMF with Sparseness Constraints, GNMFSC) 算法, 不仅考虑了数据的几何信息,并且对系数矩阵增加稀疏约束,使分解后的图像具有更高的识别率。本文将增量学习的思想引入稀疏约束图正则非负矩阵分解中,提出了稀疏约束图正则非负矩阵分解的增量学习 (Incremental learning based on GNMFSC, IGNMFSC) 算法,不仅有效地保持样本的局部结构,使算法具有较高的分类准确率,还能结合增量学习充分利用上一步的分解结果,避免重复计算从而降低运算时间。下面给出算法的迭代规则,并进行实验验证算法的有效性。
1 非负矩阵分解NMF算法具体描述如下:对给定的非负矩阵V, 寻找合适的非负基矩阵W ∈ R+m×r和非负系数矩阵H∈ R+r×n, 使得V ≈ WH。r代表基向量的个数,当r的取值满足r < < mn/(m+n) 时,原始矩阵V得到了有效的压缩。可归结为最小化下面的欧氏空间的描述形式的目标函数:
| $ \begin{array}{l} {F_{{\rm{NMF}}}} = \frac{1}{2}\left\| {\mathit{\boldsymbol{V}}-\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^T}} \right\|_F^2 = {\rm{ }}\frac{1}{2}{{\rm{(}}{\mathit{\boldsymbol{V}}_{ij}}{\rm{-(}}\mathit{\boldsymbol{WH}}{{\rm{)}}_{ij}}{\rm{)}}^{\rm{2}}}{\rm{ }}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{W}} \ge 0, \mathit{\boldsymbol{H}} \ge 0 \end{array} $ | (1) |
目标函数的乘性迭代规则为:
| $ {w_{ir}} \leftarrow {w_{ir}}\frac{{{{(\mathit{\boldsymbol{VH}})}_{ir}}}}{{{{(\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}})}_{ir}}}} $ | (2) |
| $ {h_{rj}} \leftarrow {h_{rj}}\frac{{{{({\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{W}})}_{rj}}}}{{{{\mathit{\boldsymbol{(H}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}})}_{rj}}}} $ | (3) |
其中:i=1, 2, …, m;j=1, 2, …, n。当给定迭代终止条件后,对随机生成的初始非负矩阵W0和H0, 按式 (2) 和 (3) 交替迭代更新直到满足终止条件,可得到最终的W和H。
2 IGNMFSC算法 2.1 目标函数图正则非负矩阵分解在矩阵分解过程中要求使降维后的数据保持原始数据的几何信息。在分解过程中,GNMF作如下假设:若点xi和xj在原空间中是近邻点,那么在新的基下所对应的坐标vir和vjr也一定是接近的。
设原始数据点构成的图为G,其中Sij是权矩阵,Np(xi) 表示xi的p个近邻,当xi或者xj属于Np(xi), 则Sij=1, 否则为0。定义L=D-S, D是对角矩阵,
| $ \begin{array}{l} {J_{GNMF}} = {\left\| {\mathit{\boldsymbol{V}}-\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^{\rm{T}}}} \right\|^2} + \lambda \cdot {\rm{Tr}}({\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{LH}}){\rm{ }}\\ {\rm{ s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\mathit{\boldsymbol{W}} \ge 0, \mathit{\boldsymbol{H}} \ge 0 \end{array} $ | (4) |
设Wk和Hk分别表示样本集合Vk的非负矩阵分解后得到的基矩阵和系数矩阵,Lk是样本集合Vk的拉普拉斯矩阵,r是基向量的个数,λ是正则化参数,β是稀疏系数,且β∈(0, 1), k表示当前样本集合中存在k个样本。Fk代表Vk经过非负矩阵分解后的目标函数,此时,Fk的表达式包含非负矩阵分解、图正则化、稀疏约束三项,如下所示:
| $ \begin{array}{c} {F_k} = {\left\| {\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{W}}_k}\mathit{\boldsymbol{H}}_k^{\rm{T}}} \right\|^2} + \lambda \cdot {\rm{Tr}}(\mathit{\boldsymbol{H}}_k^{\rm{T}}{\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{H}}_k}) + \beta \left\| {{\mathit{\boldsymbol{H}}_k}} \right\|_{3/2}^{3/2} = \\ \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {{{\left( {{\mathit{\boldsymbol{V}}_{ij}}-{{({\mathit{\boldsymbol{W}}_k}\mathit{\boldsymbol{H}}_k^{\rm{T}})}_{ij}}} \right)}^2}} } + \lambda \cdot {\rm{Tr}}(\mathit{\boldsymbol{H}}_k^{\rm{T}}{\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{H}}_k}) + \beta \left\| {{\mathit{\boldsymbol{H}}_k}} \right\|_{3/2}^{3/2} \end{array} $ | (5) |
当第k+1个训练样本加入后,目标函数变为:
| $ \begin{array}{c} {F_{k + 1}} = {\left\| {\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}} \right\|^2} + \lambda \cdot {\rm{Tr}}(\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{L}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}) + \beta \left\| {{\mathit{\boldsymbol{H}}_{k + 1}}} \right\|_{3/2}^{3/2} = \\ \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {{{\left( {{\mathit{\boldsymbol{V}}_{ij}}-{{({\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}})}_{ij}}} \right)}^2}} } + \lambda \cdot {\rm{Tr}}(\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{L}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}) + \beta \left\| {{\mathit{\boldsymbol{H}}_{k + 1}}} \right\|_{3/2}^{3/2} \end{array} $ | (6) |
其中:Wk+1和Hk+1分别表示样本集合Vk+1非负矩阵分解后得到的值,Lk+1是样本集合Vk+1的拉普拉斯矩阵。
2.2 迭代规则随着训练样本数量的增多,新训练样本的表达能力逐渐减小。因此当训练样本数量足够大时,新加入训练样本对于基矩阵W并不会有太大的影响,其对应的系数向量hk受到的影响也同样较小。所以当新样本vk+1到来时,系数矩阵Hk+1的前k列向量可以近似等于Hk的列向量,即Hk+1=[Hk, hk+1], 目标函数Fk+1可以重写为如下形式:
| $ \begin{array}{l} {F_{k + 1}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{k + 1} {{{\left( {{\mathit{\boldsymbol{V}}_{ij}}- {{({\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}})}_{ij}}} \right)}^2}} } + \\ \;\;\;\;\;\;\;\;\;\lambda \cdot {\rm{Tr}}(\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{L}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}) + \beta \left\| {{\mathit{\boldsymbol{H}}_{k + 1}}} \right\|_{3/2}^{3/2} \approx \\ \;\;\;\;\;\;\;\;\;\;{F_k} + \sum\limits_{i = 1}^m {{{\left( {{{({\mathit{\boldsymbol{v}}_{k + 1}})}_i}- {{({\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{h}}_{k + 1}^{\rm{T}})}_i}} \right)}^2}} + \\ \;\;\;\;\;\;\;\;\;\beta \sum\limits_{i = 1}^m {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_i^{3/2}} + \lambda \cdot [{\rm{Tr}}(\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{L}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}})-\\ \;\;\;\;\;\;\;\;\;{\rm{Tr}}(\mathit{\boldsymbol{H}}_k^{\rm{T}}{\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{H}}_k})] = {F_k} + {f_{k + 1}} \end{array} $ | (7) |
由此可以得到Fk与Fk+1之间的近似关系,这样就利用了上一步的分解结果,当加入了新的训练样本时,不需要重新迭代运算,从而降低了运算规模。fk+1表示新样本加入后损失函数的增量式,在得到目标函数的增量表达式Fk+1后,利用梯度下降法推导出相应的迭代公式。得出系数矩阵增量部分hk+1的迭代规则如下:
| $ {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a} \leftarrow {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a}-{\eta _a}\frac{{\partial {F_{k + 1}}}}{{\partial {{({\mathit{\boldsymbol{h}}_{k + 1}})}_a}}} $ | (8) |
其中:a=1, 2, …, r。
接下来计算Fk+1对hk+1的偏导数:
| $ \begin{array}{l} \frac{{\partial {F_{k + 1}}}}{{\partial {{({\mathit{\boldsymbol{h}}_{k + 1}})}_a}}} \cong \frac{{\partial ({F_k} + {f_{k + 1}})}}{{\partial {{({\mathit{\boldsymbol{h}}_{k + 1}})}_a}}} = \frac{{\partial {f_{k + 1}}}}{{\partial {{({\mathit{\boldsymbol{h}}_{k + 1}})}_a}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-2{(\mathit{\boldsymbol{v}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}})_a} + 2{({\mathit{\boldsymbol{h}}_{k + 1}}\mathit{\boldsymbol{W}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}})_a} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\left( {\mathit{\boldsymbol{\lambda h}}_{k + 1}^{\rm{T}}} \right.{\left. {{{({\mathit{\boldsymbol{L}}_{k + 1}})}_{k + 1, :}}} \right)_a} + \frac{3}{2}\beta \left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a^{1/2} \end{array} $ | (9) |
为了保证迭代过程中数据的非负性,遵循乘性迭代规则得到梯度下降的迭代步长ηa:
| $ {\eta _a} = \frac{{{{\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)}_a}}}{{2\left( {{\mathit{\boldsymbol{h}}_{k + 1}}\mathit{\boldsymbol{W}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}}} \right) + 2{{\left( {\mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{h}}_{k + 1}}{{({\mathit{\boldsymbol{D}}_{k + 1}})}_{k + 1, }}} \right)}_a} + \frac{3}{2}\beta \left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a^{1/2}}} $ | (10) |
其中:Lk+1是样本Vk+1的拉普拉斯矩阵,(Lk+1)k+1, :、(Dk+1)k+1, :和 (Sk+1)k+1, :分别为Lk+1、Dk+1和Sk+1所对应的第k+1行的行向量。
将式 (9) 和 (10) 的偏导数的值和迭代步长代入式 (8) 的迭代公式中,得到hk+1的最终迭代规则:
| $ {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a} \leftarrow {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a}\frac{{{{\left( {\mathit{\boldsymbol{v}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}} + \mathit{\boldsymbol{\lambda }} \cdot {\mathit{\boldsymbol{h}}_{k + 1}}{{({\mathit{\boldsymbol{S}}_{k + 1}})}_{k + 1, }}} \right)}_a}}}{{{{\left( {{\mathit{\boldsymbol{h}}_{k + 1}}\mathit{\boldsymbol{W}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}}} \right)}_a} + \mathit{\boldsymbol{\lambda }} \cdot {{\left( {{\mathit{\boldsymbol{h}}_{k + 1}}{{({\mathit{\boldsymbol{D}}_{k + 1}})}_{k + 1, }}} \right)}_a} + \frac{3}{4}\mu \left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a^{1/2}}} $ | (11) |
用相同的方法可以求得基矩阵W的更新规则为:
| $ {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}} \leftarrow {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}}-{\eta _{ia}}\frac{{\partial {F_{k + 1}}}}{{\partial {{({\mathit{\boldsymbol{W}}_{k + 1}})}_{ia}}}} $ | (12) |
为了区分与系数矩阵H的迭代步长,设ηia为上式中基矩阵W的迭代步长,
| $ {{\eta }_{ia}}=\frac{{{({{\mathit{\boldsymbol{W}}}_{k+1}})}_{ia}}}{2{{({{\mathit{\boldsymbol{W}}}_{k+1}}\mathit{\boldsymbol{H}}_{k}^{\rm{T}}{{\mathit{\boldsymbol{H}}}_{k}})}_{ia}}+2{{({{\mathit{\boldsymbol{W}}}_{k+1}}\mathit{\boldsymbol{h}}_{k+1}^{\rm{T}}{{\mathit{\boldsymbol{h}}}_{k}})}_{ia}}} $ | (13) |
同样地,将式 (13) 和 (14) 中的偏导数值和迭代步长代入基矩阵的迭代公式 (12) 中,得到Wk+1的迭代规则:
| $ {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}} \leftarrow {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}}\frac{{{{({\mathit{\boldsymbol{V}}_k}{\mathit{\boldsymbol{H}}_k} + {\mathit{\boldsymbol{v}}_{k + 1}}{\mathit{\boldsymbol{h}}_{k + 1}})}_{ia}}}}{{{{({\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{\mathit{\boldsymbol{H}}_k} + {\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{h}}_k^{\rm{T}}{\mathit{\boldsymbol{h}}_k})}_{ia}}}} $ | (14) |
由此,归纳IGNMFSC算法步骤如下:
1) 随机初始化正矩阵W和H;
2) 对训练样本集V (包含k个训练样本) 按以下规则进行迭代,直至满足收敛条件:
| $ {w_{ir}} \leftarrow {w_{ir}}\frac{{{{(\mathit{\boldsymbol{VH}})}_{ir}}}}{{{{(\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}})}_{ir}}}};{h_{rj}} \leftarrow {h_{rj}}\frac{{{{({\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{W}})}_{rj}}}}{{{{(\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}})}_{rj}}}} $ |
3) 当加入新训练样本vk+1时,按以下迭代规则更新W和H直至满足收敛条件,
| $ \begin{array}{l} {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a} \leftarrow {\left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a} \cdot \\ \frac{{{{\left( {\mathit{\boldsymbol{v}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}} + \mathit{\boldsymbol{\lambda }} \cdot {\mathit{\boldsymbol{h}}_{k + 1}}{{({\mathit{\boldsymbol{S}}_{k + 1}})}_{k + 1, }}} \right)}_a}}}{{{{\left( {{\mathit{\boldsymbol{h}}_{k + 1}}\mathit{\boldsymbol{W}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{W}}_{k + 1}}} \right)}_a} + \mathit{\boldsymbol{\lambda }} \cdot {{\left( {{\mathit{\boldsymbol{h}}_{k + 1}}{{({\mathit{\boldsymbol{D}}_{k + 1}})}_{k + 1, }}} \right)}_a} + \frac{3}{4}\beta \left( {{\mathit{\boldsymbol{h}}_{k + 1}}} \right)_a^{1/2}}}\\ {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}} \leftarrow {({\mathit{\boldsymbol{W}}_{k + 1}})_{ia}}\frac{{{{({\mathit{\boldsymbol{V}}_k}{\mathit{\boldsymbol{H}}_k} + {\mathit{\boldsymbol{v}}_{k + 1}}{\mathit{\boldsymbol{h}}_{k + 1}})}_{ia}}}}{{{{({\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{\mathit{\boldsymbol{H}}_k} + {\mathit{\boldsymbol{W}}_{k + 1}}\mathit{\boldsymbol{h}}_k^{\rm{T}}{\mathit{\boldsymbol{h}}_k})}_{ia}}}} \end{array} $ |
其中:Hk+1=[Hk, hk+1], hk+1初始化为hk。
3 实验结果及分析实验环境:Windows 7操作系统,CPU为3.30 GHz,内存8 GB,程序环境为Matlab R2014b。
3.1 数据描述及参数设置实验采用标准人脸库ORL和PIE人脸库进行算法的有效性验证。ORL人脸数据库包含40人面部图像,每人10种不同的姿态;在每个类取6个共240个作为训练样本,迭代次数设为200。PIE人脸数据库 (PIE_pose子集) 含68名志愿者面部姿态以及表情图像,共有170种不同的拍摄条件,共11560幅图像;在每个类取100个共6800个作训练样本,迭代次数为150。
IGNMFSC算法模型中有两个关键的折中参数:正则项参数λ和稀疏约束β。
为了确定正则项参数λ, 分别在选取的两个数据集上进行实验。从实验结果来分析,IGNMFSC算法在λ在10~500变化时,其值对文章讨论的运行时间和稀疏度影响不大,根据实际经验,在两个数据集取λ=100。同样,稀疏系数β的值也通过实验结果确定,β∈(0, 1), 若稀疏系数β的值太大会使图像过于稀疏导致不能很好地表示,根据文献[12]提供的一种用准确率和归一化互信息两个指标决定验证算法有效性的思想,分别在两个数据集上进行实验,研究了β值的选取对准确率和归一化互信息的影响。通过对比实验,在ORL数据集上稀疏约束β设为0.3,PIE数据集上稀疏约束β设为0.6。
3.2 运行时间对比在ORL人脸数据库上,初始训练样本为240时NMF[1]、INMFSC[4]、GNMFSC[7]和本文IGNMFSC算法随新增样本数量的增多而消耗的时间如表 1所示;在PIE数据集上,初始训练样本为6 800时算法的时间消耗如表 2所示。
| 表 1 ORL库新增训练样本时不同算法的时间消耗 s Table 1 Time cost for adding training samples on ORL database s |
| 表 2 PIE库新增训练样本时不同算法的时间消耗 s Table 2 Time cost for adding training samples on PIE database s |
由表 1~2可知,与几种对比算法相比,本文算法在运算时间上有明显优势,而当新增训练样本超过一定数量时,IGNMFSC算法仍能保持相对高的运算效率。
3.3 稀疏度的度量度量稀疏度的函数为:
| $ sparseness(\mathit{\boldsymbol{x}}) = \frac{1}{{n- 1}}[n-{(\frac{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_1}}}{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_2}}})^2}] $ | (15) |
其中:n是向量x的维度,‖·‖1是向量的1范数,‖·‖2是向量的2范数,0≤sparseness(x)≤1。当x仅有一个非零元素时, 函数值为1;当所有元素都不为零且相等时,函数值为0。
以式 (15) 作为稀疏度度量标准,则经过NMF[1]、INMFSC[4]、GNMFSC[7]和本文IGNMFSC几种算法分解后得到的基矩阵W和系数矩阵H的稀疏度如表 3所示。
| 表 3 几种算法得到的因子矩阵稀疏度 Table 3 Sparsity of factor matrix obtained by several algorithms |
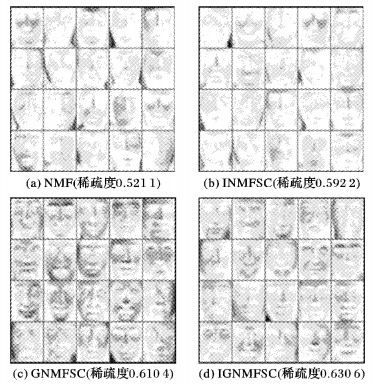
图 1~2表示在数据库ORL和PIE上的基图像。其中,ORL数据集的基矩阵特征维数取36,PIE数据集的基矩阵特征维数取20。由图 1~2可以看出,NMF算法的基向量最接近原图像,容易得到原始样本的最优表示,但是它的稀疏度较差,存储效率低。同其他的NMF改进算法相比,IGNMFSC算法能得到更稀疏的基图像,由此表明算法得到了图像的最佳的局部表示。

|
图 1 ORL数据集的基图像 (r=36) Figure 1 Basis vectors learned on ORL dataset (r=36) |
|
图 2 PIE数据集的基图像 (r=20) Figure 2 Base images learned on PIE dataset (r=20) |
本文提出了稀疏约束图正则非负矩阵分解的增量学习算法,并给出了相应的迭代规则和算法步骤。以ORL人脸库和PIE人脸库的数据作为实验对象进行验证,结果显示本文算法不仅缩短了运行时间,而且使分解后的数据更为稀疏,能得到局部表达能力和判别能力更强的基图像。
| [1] | LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401 (6755) : 788-791. doi: 10.1038/44565 |
| [2] | HOYER P O. Non-negative matrix factorization with sparseness constraints[J]. Journal of Machine Learning Research, 2004, 5 (1) : 1457-1469. |
| [3] | SERHAT S, BUCA B, GUNSEL. Incremental subspace learning via non-negative matrix factorization[J]. Pattern Recognition, 2009, 42 (5) : 788-797. doi: 10.1016/j.patcog.2008.09.002 |
| [4] | 王万良, 蔡竞. 稀疏约束下非负矩阵分解的增量学习算法[J]. 计算机科学, 2014, 41 (8) : 241-244. ( WANG W L, CAI J. Incremental learning algorithm of non-negative matrix factorization with sparseness constraints[J]. Computer Science, 2014, 41 (8) : 241-244. ) |
| [5] | LIU H, WU Z, LI X, et al. Constrained non-negative matrix factorization for image representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34 (7) : 1299-1311. doi: 10.1109/TPAMI.2011.217 |
| [6] | CAI D, HE X, HAN J, et al. Graph regularized non-negative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33 (8) : 1548-1560. doi: 10.1109/TPAMI.2010.231 |
| [7] | 姜伟, 李宏, 于震国, 等. 稀疏约束图正则非负矩阵分解[J]. 计算机科学, 2013, 40 (1) : 218-256. ( JIANG W, LI H, YU Z G, et al. Graph regularized non-negative matrix factorization with sparseness constraints[J]. Computer Science, 2013, 40 (1) : 218-256. ) |
| [8] | 李乐, 章毓晋. 非负矩阵分解算法综述[J]. 电子学报, 2008, 36 (4) : 737-743. ( LI L, ZHANG Y J. A survey on algorithms of non-negative matrix factorization[J]. Acta Electronica Sinica, 2008, 36 (4) : 737-743. ) |
| [9] | 胡丽莹, 郭躬德, 马昌凤. 基于对称非负矩阵分解的重叠社区发现方法[J]. 计算机应用, 2015, 35 (10) : 2742-2746. ( HU L Y, GUO G D, MA C F. Overlapping community discovery method based on symmetric nonnegative matrix factorization[J]. Journal of Computer Applications, 2015, 35 (10) : 2742-2746. ) |
| [10] | 姜小燕. 基于基于非负矩阵分解的图像分类算法研究[D]. 锦州: 辽宁工业大学, 2016. ( JIANG X Y. Research on image classification algorithm based on non-negative matrix factorization[D]. Jinzhou: Liaoning University of Technology, 2016. ) |
| [11] | 汪金涛, 曹玉东, 王梓宁, 等. 图像型垃圾邮件监控系统研究与设计[J]. 辽宁工业大学学报 (自然科学版), 2016, 36 (2) : 78-81. ( WANG J T, CAO Y D, WANG Z N, et al. Research and design of monitoring system on image spam[J]. Journal of Liaoning University of Technology (Natural Science Edition), 2016, 36 (2) : 78-81. ) |
| [12] | 胡学考, 孙福明, 李豪杰. 基于稀疏约束的半监督非负矩阵分解算法[J]. 计算机科学, 2015, 42 (7) : 280-304. ( HU X K, SUN F M. LI H J. Constrained nonnegative matrix factorization with sparseness for image representation[J]. Computer Science, 2015, 42 (7) : 280-304. ) |
| [13] | 杜世强, 石玉清, 王维兰, 等. 基于图正则化的半监督非负矩阵分解[J]. 计算机工程与应用, 2012, 48 (36) : 194-200. ( DU S Q, SHI Y Q, WANG W L, et al. Graph-regularized-based semi-supervised non-negative matrix factorization[J]. Computer Engineering and Applications, 2012, 48 (36) : 194-200. ) |




