2. 西华师范大学 计算机学院, 四川 南充 637009
2. Computer School, China West Normal University, Nanchong Sichuan 637009, China
有序决策问题,即条件属性和决策属性均存在序结构的决策问题,是多规则决策中的一类重要问题。在这种系统中,被评估对象往往由一组属性(条件属性)描述,在决策分析领域,把这一类问题统称为多标准有序决策(或偏好分析)问题[1-3]。有序决策问题在实际应用中广泛出现,如投稿论文的录用决策、人力资源考核、信誉评估、投资风险分析以及学生评定等。
对于有序决策问题,通常分为两种情况。一种是偏好一致的有序决策,在这种系统中,隐含的一致性假设为,条件属性值越大的对象,其决策往往也更好。比如在学生评定系统中,如果学生甲与学生乙其他各方面的表现都完全相同,但学生甲的创新能力比学生乙强,那么,如果学生乙被评定为优秀,那么学生甲也应该评为优秀。另一种就是偏好不一致的有序决策。在这种系统中,存在一些对象,其拥有更好的条件属性值,但其决策却更差。对于偏好一致的有序决策系统,决策方法比较简单,但在现实应用当中,由于可用信息的多规则和多源性,更多地是偏好不一致的情况。显然,由于偏好的不一致性,导致其决策往往具有不确定性。
1948年,Shannon[4]指出,任何信息都存在冗余,冗余大小与信息中每个符号(数字、字母或单词)的出现概率或者说不确定性有关,并借鉴了热力学的概念,定义了信息熵来表示信息中排除了冗余后的平均信息量。从此,信息熵成为了度量不确定性的重要工具,许多研究者把信息熵拓展到了各种不同领域,定义了各种各样的信息熵[5-8]。在有序决策研究领域,2009年,Hu等[9]提出排序熵和排序互信息的概念,并且应用排序互信息来启发式构建有序决策树[10]。此算法较好地体现出序的结构信息,但是此算法在扩展属性选取时,需度量每个属性取值,在大规模的训练集且样例的每个属性取值不同的情况下,其计算复杂度会很高[11]。文献[12]定义了偏好不一致熵,用来度量多规则有序决策中各属性由于偏好不一致带来的决策不确定程度,并将其应用于特征选择和样本压缩。该熵是基于属性的,熵值的大小能够反映出该条件属性对决策的重要程度。
本文借鉴文献[12]的基本思想,基于有序决策的基本目标,定义了一种新的偏好不一致熵(样本的偏好不一致熵)。样本的偏好不一致熵能够表示每一个样本的偏好不一致程度。一个样本被赋予不同的决策,它的偏好不一致熵也是不一致的。熵值越大,表示该决策会导致较大的不确定性;熵值越小,该决策就越趋合理。在多规则决策中,不同的属性的重要程度是不一样的。本文以文献[12]提出的偏好不一致熵作为属性重要度加权,提出了一种多规则有序决策方法。
1 偏好关系与偏好不一致熵在这一部分,将简单介绍文献[12]中介绍和定义的偏好关系与偏好不一致熵等基本概念。
1.1 偏好关系一个决策系统是一个元组PS=〈U, C∪D〉,其中,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d2, …, dn}是决策集。如果d1<d2<…<dn ,并且ai1<ai2<…<aik对所有的ai∈C均成立,决策系统PS就被称为有序决策系统。其中,{ai1, ai2, …, aik}是条件属性ai的值集。给定一个有序决策系统PS=〈U, C∪D〉,偏好关系被定义为:
| $R_C^ \ge = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}a} \right) \le f\left( {y,{\rm{ }}a} \right),\forall a \in C} \right\}$ | (1) |
| $R_C^ \ge = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}a} \right) \le f\left( {y,{\rm{ }}a} \right),\forall a \in C} \right\}$ | (2) |
| $R_D^ \ge = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}D} \right) \ge f\left( {y,{\rm{ }}D} \right)} \right\}$ | (3) |
| $R_D^ \ge = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}D} \right) \le f\left( {y,{\rm{ }}D} \right)} \right\}$ | (4) |
| $R_C^ > = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}a} \right) > f\left( {y,{\rm{ }}a} \right),\forall a \in C} \right\}$ | (5) |
| $R_C^ < = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}a} \right) < f\left( {y,a} \right),\forall a \in C} \right\}$ | (6) |
| $R_D^ > = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}D} \right) > f\left( {y,{\rm{ }}D} \right)} \right\}$ | (7) |
| $R_D^ < = \left\{ {\left( {x,{\rm{ }}y} \right) \in U \times U|f\left( {x,{\rm{ }}D} \right) > f\left( {y,{\rm{ }}D} \right)} \right\}$ | (8) |
其中: f{x, a}是对象x在属性a的取值,f{x, D}是对象x的决策。R≥和R>均被称为向上的偏好关系,R≤和R<均被称为向下的偏好关系。
如果(x, y)∈RC≥,称对象x在条件C上不弱于对象y;如果(x, y)∈RC>,称对象x在条件C上优于对象y;如果(x, y)∈RC≤,称对象x在条件C上不优于对象y;如果(x, y)∈RC<,称对象x在条件C上不及对象y。同理,如果(x, y)∈RD≥,称对象x的决策不弱于对象y;如果(x, y)∈RD>,称对象x的决策优于对象y;如果(x, y)∈RD≤,称对象x的决策不弱于对象y;如果(x, y)∈RD<,称对象x的决策不及对象y。
根据偏好关系的定义,偏好信息粒子被定义为:
| $\left[ x \right]_C^ \ge = \{ y|\left( {y,{\rm{ }}x} \right) \in R_C^ \ge \} $ | (9) |
| $\left[ x \right]_C^ \le = \{ y|\left( {y,{\rm{ }}x} \right) \in R_C^ \le \} $ | (10) |
| $\left[ x \right]_C^ > = \{ y|\left( {y,{\rm{ }}x} \right) \in R_C^ > \} $ | (11) |
| $\left[ x \right]_C^ < = \{ y|\left( {y,{\rm{ }}x} \right) \in R_C^ < \} $ | (12) |
给定有序决策系统PS=〈U, C∪D〉,如果∀x∈U, y∈[x]a>,都有f(y, D)≥f(x, D)成立,称有序决策系统PS是向上偏好一致的;反之,PS是向上偏好不一致的。类似地,如果∀x∈U, y∈[x]a<,都有f(y, D)≤f(x, D)成立,称有序决策系统PS是向下偏好一致的;反之,PS是向下偏好不一致的。如果一个有序决策是系统既是向上偏好一致的,又是向下偏好一致的,称该系统是全局偏好一致系统;反之,则称之为非全局偏好一致系统,简称为偏好不一致系统。
1.2 偏好不一致熵定义 1[12] 给定偏好不一致的有序决策系统PS=〈U, C∪D〉,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是决策集。∀x∈U, A⊆C,其向上的偏好不一致集和向下的偏好不一致集可分别表示为uiconS(x, a)和diconS(x, a)。
| $uiconS\left( {x,a} \right) = \left\{ {y \in \left[ x \right]_b^ > |f\left( {y,D} \right) < f\left( {x,{\rm{ }}D} \right),{\rm{ }}\forall b \in B} \right\}$ | (13) |
| $diconS\left( {x,{\rm{ }}a} \right) = \left\{ {y \in \left[ x \right]_b^ < |f\left( {y,{\rm{ }}D} \right) > f\left( {x,{\rm{ }}D} \right),{\rm{ }}\forall b \in B} \right\}$ | (14) |
可以很容易地得到如下结论。
| $uiconS\left( {x,a \cup b} \right) = uiconS\left( {x,a} \right) \cap uiconS\left( {x,b} \right)$ | (15) |
| $diconS\left( {x,a \cup b} \right) = diconS\left( {x,a} \right) \cap diconS\left( {x,b} \right)$ | (16) |
定义 2[12] 给定偏好不一致的有序决策系统PS=〈U, C∪D〉。∀A⊆C, x∈U,偏好不一致度(PICD)可以定义为:
向上偏好不一致度:
| $upicd\left( {x,A} \right) = \left| {uiconS\left( {x,A} \right)} \right|/\left| U \right|$ | (17) |
向下偏好不一致度:
| $dpicd\left( {x,{\rm{ }}A} \right) = \left| {diconS\left( {x,{\rm{ }}A} \right)} \right|/\left| U \right|$ | (18) |
对于偏好不一致度,∀a1, a2⊆C有如下公式成立。
| $upicd(x,{\rm{ }}{a_1}) \ge upicd(x,{\rm{ }}{a_1} \cup {a_2})$ | (19) |
| $upicd(x,{\rm{ }}{a_2}) \ge upicd(x,{\rm{ }}{a_1} \cup {a_2})$ | (20) |
| $dpicd(x,{\rm{ }}{a_1}) \ge upicd(x,{\rm{ }}{a_1} \cup {a_2})$ | (21) |
| $dpicd(x,{\rm{ }}{a_2}) \ge upicd(x,{\rm{ }}{a_1} \cup {a_2})$ | (22) |
偏好不一致度反映了有序决策系统中样本x的条件属性a与决策的偏好不一致程度:值越大,不一致程度就越高;值越小,一致度就越高;值为0,则表明属性与决策完全一致。属性与决策的偏好不一致,导致了决策的不确定性。
香农信息熵是度量不确定性的有力工具。假设X是一随机变量,x1, x2, …, xn是X的n个可能取值,其概率分布分别为p1, p2, …, pn,且满足
| $H\left( x \right) = - \sum\limits_{i = 1}^n {{p_i}{\rm{lb}}{p_i}} $ | (23) |
用偏好不一致度代替香农信息熵中的概率p, 可得到偏好不一致熵。
定义 3[12] 给定偏好不一致的有序决策系统PS=〈U, C∪D〉,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是有序决策集。∀A⊆C,属性A的偏好不一致熵(Preference Inconsistence-based Entropy, PIE)能被定义为:
向上的偏好不一致熵:
| $UAH\left( A \right) = - \frac{1}{{\left| U \right|}}\sum\limits_{x \in U} {{\rm{lb}}\left( {1 - upicd\left( {x,{\rm{ }}A} \right)} \right)} $ | (24) |
向下的偏好不一致熵:
| $DAH\left( A \right) = - \frac{1}{{\left| U \right|}}\sum\limits_{x \in U} {{\rm{lb}}\left( {1 - dpicd\left( {x,{\rm{ }}A} \right)} \right)} $ | (25) |
定义3定义的偏好不一致熵能度量属性与决策的偏好不一致所引起的决策不确定性大小。由定义3可以看出,偏好不一致熵都是大于或等于0的。偏好不一致熵大于0则表示该属性(或属性子集)与决策是偏好不一致的。熵值越大,属性(或属性子集)与决策是偏好不一致度就越大,由此属性作出决策的不确定性就越大。熵等于0则表示该属性与决策是偏好一致的,决策的偏好对该属性是确定的。显然,熵值越小,属性与决策的一致度就越高,属性对决策的影响就越大,该属性对决策就越重要,因此,基于属性的偏好不一致熵的特征选择和属性约简是合适的。
偏好分析的一个重要任务是偏好决策。也就是说,给定一个未知决策的样本,需要以训练样本集为参照,通过分析样本条件属性的偏好,为其赋予一个最合适的类标签。对于样本分类,需要度量样本与整个样本集的一致程度,显然,定义3定义的基于属性的偏好不一致熵不具有这方面的能力。在下文将定义样本的偏好不一致熵,并将其应用于样本分类。
2 样本的偏好不一致熵与偏好决策定义 4 给定偏好不一致的有序决策系统PS=〈U, C∪D〉,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是有序决策集。∀x∈U,定义样本x的偏好不一致熵(Preference Inconsistence-based Entropy of Object, PIEO)如下。
向上的偏好不一致熵:
| $UOH\left( x \right) = - \frac{1}{m}\sum\limits_{a \in C} {{\rm{lb}}(1 - upicd(x,{\rm{ }}{a_i}))} $ | (26) |
向下的偏好不一致熵:
| $DOH\left( x \right) = - \frac{1}{m}\sum\limits_{a \in C} {{\rm{lb}}(1 - dpicd(x,{\rm{ }}{a_i}))} $ | (27) |
全局偏好不一致熵:
| $\begin{array}{l} ROH\left( x \right) = - \frac{1}{2}\left( {(DOH\left( x \right) \times {\rm{lb}}\left( {1 - DOH\left( x \right)} \right)} \right) + \\ \left. {UOH\left( x \right){\rm{ \times lb}}\left( {1 - UOH\left( x \right)} \right)} \right) \end{array}$ | (28) |
与属性的偏好不一致熵度量的是特定属性或属性集合在偏好决策中的重要程度不同,样本的偏好不一致熵反映的是特定样本与整个训练样本集的偏好不一致程度。熵值越小,样本与训练样本集的一致度就越大。在有监督的偏好决策中,为测试样本赋予不同的类别,其偏好不一致熵通常是不一样的,偏好不一致熵最小的决策应为最优决策。
在多规则决策系统中,不同的条件属性对决策的影响通常是不一样的。定义4的样本的偏好不一致熵没有考虑不同属性对决策影响的差异。通过前面的分析可以知道,定义3给出的属性的偏好不一致熵能够有效反映属性对决策的重要程度。熵值越小,属性对决策越重要。用属性的偏好不一致熵进行加权,可以得到样本的偏好不一致熵的改进形式。
定义 5 给定偏好不一致的有序决策系统PS=〈U, C∪D〉,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是有序决策集。∀x∈U,定义样本x的加权的偏好不一致熵(weighted Preference Inconsistence-based Entropy of Object, wPIEO)如下。
向上的偏好不一致熵:
| $UWH\left( x \right) = - \frac{1}{m}\sum\limits_{a \in C} {w\left( a \right) \times {\rm{lb}}\left( {1 - upicd\left( {x,{\rm{ }}a} \right)} \right)} $ | (29) |
向下的偏好不一致熵:
| $DWH\left( x \right) = - \frac{1}{m}\sum\limits_{a \in C} {w\left( a \right) \times {\rm{lb}}\left( {1 - dpicd\left( {x,{\rm{ }}a} \right)} \right)} $ | (30) |
全局偏好不一致熵:
| $\begin{array}{l} RWH\left( x \right) = - \frac{1}{2}\left. {((DWH\left( x \right) \times {\rm{lb}}\left( {1 - DWH\left( x \right)} \right)} \right) + \\ \left. {UWH\left( x \right) \times {\rm{lb}}\left( {1 - UWH\left( x \right)} \right)} \right) \end{array}$ | (31) |
其中,w(a)是属性的重要性权值。w(a)>0,
| $w\left( a \right) = \frac{{W\left( a \right)}}{{\sum\limits_{a \in C} {W\left( a \right)} }}$ | (32) |
| $W\left( a \right)=\left\{ \begin{matrix} 1/AH\left( a \right), & AH\left( a \right)\ne 0 \\ N, & AH\left( a \right)=0 \\ \end{matrix} \right.$ | (33) |
其中:N为大于max(1/AH(a))(AH(a)≠0时)的常数,AH为定义3定义的关于属性的偏好不一致熵。计算UWH时,AH为UAH;计算DWH时,AH为DAH。AH(a)=0,表明属性a与决策偏好一致,其重要性非常高,因此需要为其赋予更大的权值,通常取N取3~5倍的max(1/AH(a))。
对于偏好不一致有序决策系统PS=〈U
| $L\left( x \right) = \mathop {{\rm{arg min}}}\limits_d \left( {OH} \right)$ | (34) |
其中,OH表示样本的偏好不一致熵。对于向上的偏好决策,OH为UOH;对于向上的偏好决策,OH就为DOH。
下面将给出一种基于样本偏好不一致熵的样本分类算法。
算法 1 基于PIEO的样本分类算法(CPIEO)。
输入:有序决策系统PS=〈U, C∪D〉, 待分类样本x;输出:样本x的类别y;
1) for each a in C
2) 计算各属性的偏好不一致熵AH(a);
3) if AH(a)≠0
4) W(a)=1/AH(a);
5) else
6) W(a)=N;
7) end if
8) end for
9) for each a in C
10) w(a)=W(a)/∑W(a);
11) end for
12) for each d in D
13) f(x, D)=d;
14) U=U∪{x};
15) 计算样本x的加权偏好不一致熵pieo(d)=WH(x);
16) end for
17)
18) return y
算法的时间复杂度为O(n)(n为决策系统条件属性的个数)。由于样本的类别通常都只有有限的几项,因此该算法的时间消耗主要由偏好不一致熵的时间决定。如果希望决策尽可能好,则可以用向上的偏好不一致熵进行计算;如果希望决策尽可能差,则应用向下的偏好不一致熵进行计算;否则,应该用全局的偏好不一致熵进行计算。
3 实验分析本文从WEKA(http://www.cs.waikato.ac.nz/ml/weka/)下载了两个数据集:Pasture Production和Squash Harvest。将基于这两个数据集通过实验来分析本文所提出的偏好决策算法的性能和有效性。为此,针对有序决策系统的特点,本文定义了分类偏离度和分类偏好一致度来度量分类的效果。
定义 6 假设PS=〈U, C∪D〉是偏好不一致有序决策系统。其中,U是非空对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是决策集。∀x∈U,c(x)是对象x被赋予的类标签,o(x)是对象x的原始类标签。本文定义分类偏离度为:
| $ddc = \left( {\sum\limits_{x \in U} {\left| {c\left( x \right) - o\left( x \right)} \right|} } \right)/\left( {\left| U \right| \times n} \right)$ | (35) |
定义 7 假设PS=〈U, C∪D〉是偏好不一致有序决策系统,U是非空有限对象集,C={a1, a2, …, am}是条件属性集,D={d1, d1, …, dn}是决策集。∀x∈U,c(x)是对象x被赋予的类标签,o(x)是对象x的原始类标签。本文定义分类偏好一致度如下。
向上的分类一致度:
| $ucdc = \left( {\sum\limits_{x \in U} {\left| {c\left( x \right) \ge o\left( x \right)} \right|} } \right)/\left| U \right|$ | (36) |
向下的分类一致度:
| $dcdc = \left( {\sum\limits_{x \in U} {|c\left( x \right) \le o\left( x \right)|} } \right)/\left| U \right|$ | (37) |
在分类问题中,通常用分类的准确度来评价一个算法的优劣,但具体到多规则的有序决策问题中,除了要分析分类的准确度之外,还需要分析决策的决策者的偏好问题,因此,本文定义了分类偏离度和偏好一致度分别从这两个维度来对决策算法进行分析。分类偏离度反映的是分类结果与测试样本原始类别的偏离程度,分类偏离度越小,分类的准确度就越高,算法就越好。分类偏好一致度度量的是分类结果与原始决策的偏好一致程度,分类偏好一致度越大,算法就越能反映决策者的偏好,算法也就越好。下面,就用这两个指标来对分析提出的算法的有效性。
数据集Pasture Production是由Dave Barker在1973—1994年间从北岛地区收集的,其目的是要分析各种生物和物理因素对牧场生产的影响。该数据集收集了36个样本,每个样本记录了一个围场的相关数据。每个样本包括22个属性,其中19个是植被情况,其余3个分别表示土壤的化学成分、物理和生物特性,以及土壤水分变化。所有的记录都被分成了三个类别,高、中、低,分别表示该围场的产量情况。
数据集Squash Harvest是由新西兰的一家作物与食品研究机构收集的。收集该数据集的目的是为了研究南瓜在成熟和运输过程中的各种变化,以确定最佳的采摘时间,以便在运到日本市场后能有最好的口感。Squash Harvest数据集共采集了52个样本,每个样本包括24个属性指标。样本的质量被分为了不可接受、可接受和很好三个等级。为便于计算和处理,分别用1、2和3来分别表示这三个等级。为便于表示,把数据集Pasture Production的条件属性依次标记为1,2,3,…,21,22,把数据集Squash Harvest的条件属性依次标记为1,2,3,…,23,24。
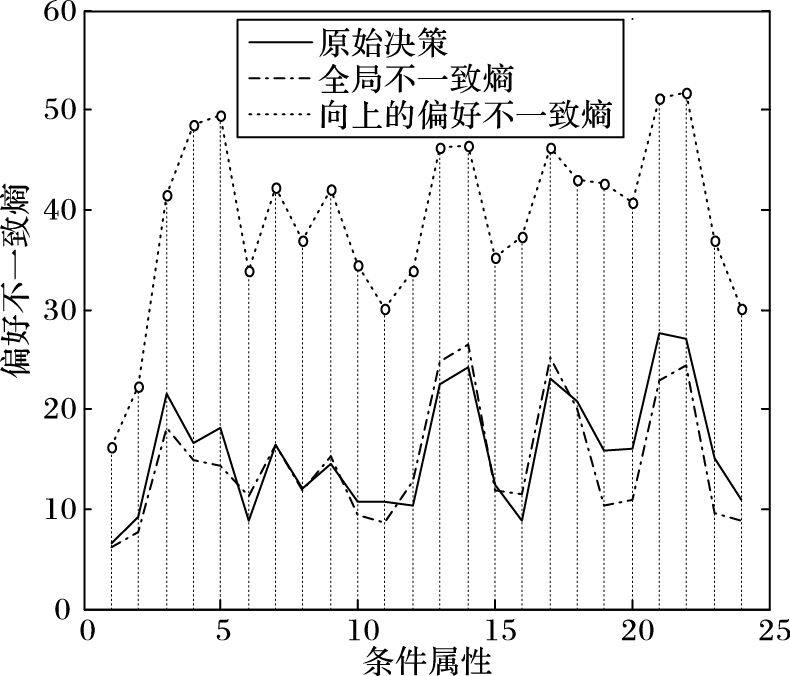
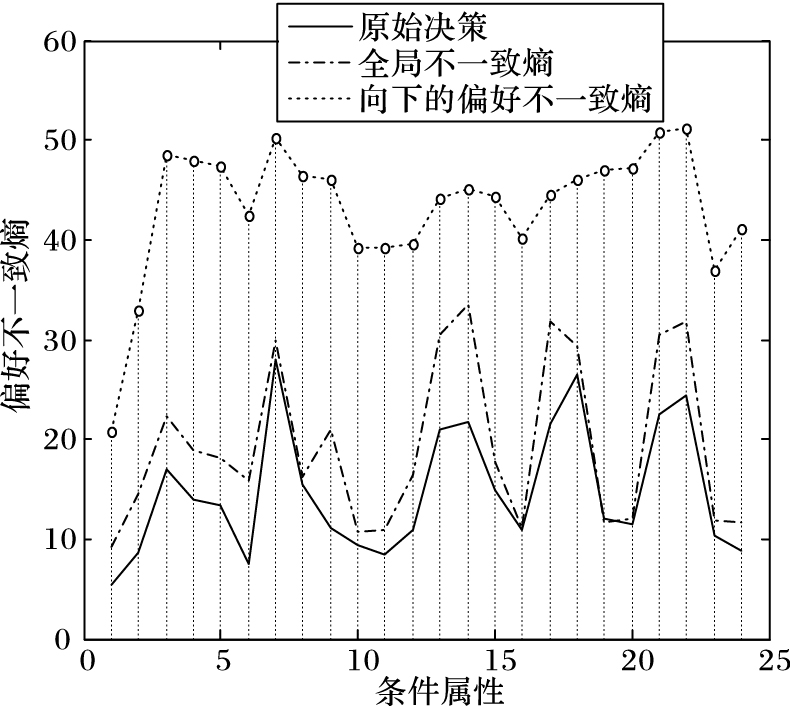
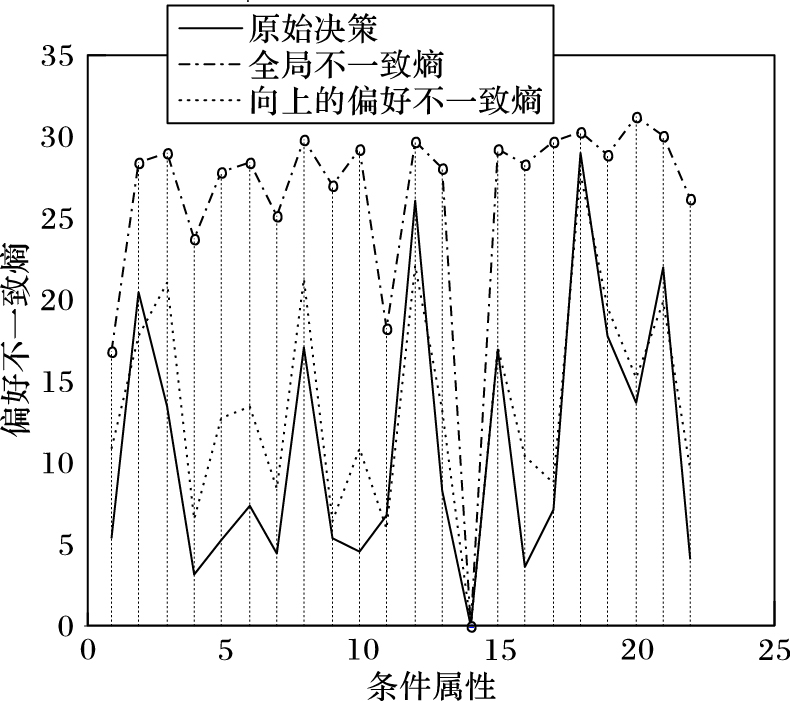
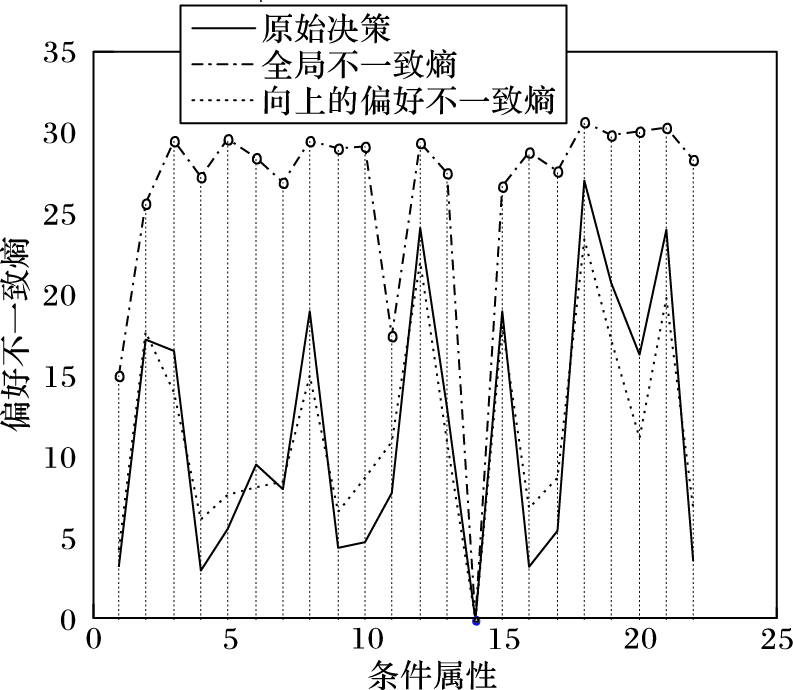
为了便于比较,用基于属性的偏好不一致熵(PIE)来度量各种情况下的分类效果。图 1~4展示了Squash Harvest和Pasture Production两个数据集在原始决策、基于全局偏好不一致熵分类、基于向上偏好不一致熵和向下偏好不一致熵分类情况下各属性的偏好不一致熵。其中的曲线为各种情况下得到的属性的偏好不一致熵的包络。从图 1和图 3可以看出,基于全局偏好不一致熵分类后,各属性的向上偏好不一致熵与原始决策的向上偏好不一致熵非常接近(甚至有部分属性的向上偏好不一致熵比原始决策的向上偏好不一致熵更小),而从图 2和图 4则可以发现各属性的向下偏好不一致熵普遍比原始决策的向下偏好不一致熵略大,这说明这两个数据集的原始决策均是基于向上的偏好做出的;同时还可以看出,基于全局偏好不一致熵分类后,其各属性的偏好不一致熵普遍比基于向上和向下偏好不一致熵分类后的熵值小,而且更接近原始决策的偏好不一致熵,这说明基于全局偏好不一致熵的分类比其他两种情况的分类效果好。
|
图 1 向上的偏好不一致熵(Squash) Figure 1 Upward preference-inconsistent entropy (Squash) |
|
图 2 向下的偏好不一致熵(Squash) Figure 2 Downward preference-inconsistent entropy (Squash) |
|
图 3 向上的偏好不一致熵(Pasture) Figure 3 Upward preference-inconsistent entropy (Pasture) |
|
图 4 向下的偏好不一致熵(Pasture) Figure 4 Downward preference-inconsistent entropy (Pasture) |
表 1是Squash Harvest和Pasture Production两个数据集在各种情况下进行分类的分类偏离度和分类偏好一致度的比较。其中,RWH表示样本的全局偏好不一致熵,UWH表示样本的向上偏好不一致熵,DWH表示样本的向下偏好不一致熵。
| 表 1 不同偏好不一致熵方法分类效果比较 Table 1 Classification effect comparison of different preference inconsistent entropy methods |
表 1的第2和第5行是基于样本的全局偏好不一致熵得到的结果,第3和第6行是基于样本的向上偏好不一致熵得到的结果,第4和第7行是基于样本的向下偏好不一致熵得到的结果。从表 1可以看出:各种情况下的分类偏离度都不大,最低为0.128 2,最大为0.282 1,这说明各种情况下的偏好决策均与原始决策比较接近;而由于原始决策的偏好不一致,各种情况下的分类偏好一致度波动相对较大,但均大于0.5,这说明分类结果与原始决策的偏好是基本一致的。
4 结语针对偏好不一致有序系统中的样本决策问题,基于偏好信息粒子和样本的偏好不一致度,定义了样本的偏好不一致熵,并扩展到加权的偏好不一致熵,进而提出了样本的偏好决策算法。为了评价算法的有效性,依据偏好决策的特点,定义了分类偏离度和分类偏好一致度来度量偏好决策的合理性。
采用Pasture Production和Squash Harvest两个数据集进行仿真实验。实验结果表明,提出的方法在解决偏好不一致有序决策系统中的样本分类问题方面具有较好的效果,当基于全局偏好不一致熵进行分类时,能够得到与原始决策比较接近的结果;但是,在实验中也发现,由于偏好的不一致导致了决策的不确定性,分类的准确度不是很高。在以后的工作中,将进一步对相关的模型和算法进行分析,研究提高分类准确度的方法。
| [1] | BŁASZCZYNSKI J, GRECO S, SŁOWINSKI R. Multi-criteria classification-a new scheme for application of dominance-based decision rules[J]. European Journal of Operational Research, 2007, 181 (3) : 1030-1044. doi: 10.1016/j.ejor.2006.03.004 |
| [2] | WANG Y M, PARKAN C. Optimal aggregation of fuzzy preference relations with an application to broadband Internet service selection[J]. European Journal of Operational Research, 2008, 187 (3) : 1476-1486. doi: 10.1016/j.ejor.2006.09.026 |
| [3] | 徐泽水. 基于不同类型残缺判断矩阵的群决策方法[J]. 控制与决策, 2006, 21 (1) : 28-33. ( XU Z S. Group decision making method based on different types of incomplete judgment matrices[J]. Control and Decision, 2006, 21 (1) : 28-33. ) |
| [4] | SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948 (3) : 379-423. |
| [5] | YANG J, QIU W. A measure of risk and a decision-making model based on expected utility and entropy[J]. European Journal of Operational Research, 2005, 164 (3) : 792-799. doi: 10.1016/j.ejor.2004.01.031 |
| [6] | ZENG K, SHE K, NIU X. Multi-granulation entropy and its application[J]. Entropy, 2013, 15 : 2288-2302. doi: 10.3390/e15062288 |
| [7] | HU Q H, YU D R. Neighborhood entropy[C]//Proceedings of the 2009 International Conference on Machine Learning and Cybernetics. Piscataway, NJ:IEEE, 2009,3:1776-1782. |
| [8] | LOTFI F H, FALLAHNEJAD R. Imprecise Shannon's entropy and multi attribute decision making[J]. Entropy, 2010, 12 : 53-62. doi: 10.3390/e12010053 |
| [9] | HU Q, GUO M, YU D, et al. Information entropy for ordinal classification[J]. Science China (Information Sciences), 2010, 53 (6) : 1188-1200. doi: 10.1007/s11432-010-3117-7 |
| [10] | HU Q, CHE X, ZHANG L, et al. Rank entropy-based decision trees for monotonic classification[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24 (11) : 2052-2064. doi: 10.1109/TKDE.2011.149 |
| [11] | 陈建凯, 王熙照, 高相辉. 改进的基于排序熵的有序决策树算法[J]. 模式识别与人工智能, 2014, 27 (2) : 134-140. ( CHEN J K, WANG X Z, GAO X H. Improved ordinal decisions trees algorithms based on rank entropy[J]. Pattern Recognition and Artifical Intelligence, 2014, 27 (2) : 134-140. ) |
| [12] | PAN W, SHE K, WEI P. Preference inconsistence-based entropy[J]. Entropy, 2016, 18 : 96. doi: 10.3390/e18030096 |




