旅行商问题(Traveling Salesman Problem, TSP)即给定一组城市及它们两两之间的距离,求经过每座城市恰一次并返回出发地的最短路线问题[1],它是典型的NP-难(Non-deterministic Polynomial Hard, NP-hard )问题[2],自1949年被Robinson[3]首次提出后,至今为止仍然没有很好的解决方案。20世纪以来,群体智能的诞生使优化领域得到了很大的发展,科学家们通过模仿自然界的规律设计出了求解复杂优化问题的仿生智能算法,如:遗传算法(Genetic Algorithm, GA)[4]、蚁群算法(Ant Colony Optimization, ACO)[5]、人工蜂群(Artificial Bee Colony, ABC)算法[6]、粒子群优化(Particle Swarm Optimization, PSO)算法[7-8]等。这些智能算法的出现,为解决TSP提供了更好的解决方案。如刘朝华等[9-10]使用免疫算法及其与蚁群算法融合的混合算法求解TSP,并做了大量的相关性研究,改进后的算法求解TSP时收敛速度更快、精度更高;姚明海等[11] 利用改进的模拟退火和遗传算法求解TSP,设计的改进算法在初始解的选择、新解的生成、当前解的改良及交叉方式等方面提出了新的观点,这在很大程度上提高了最优解的搜索速度。除这些算法外,粒子群算法也是用于求解TSP的重要算法之一。
粒子群优化算法是一种群智能算法,最早由Kennedy和Eberhart提出的,它是对鸟群和鱼群捕食过程的模拟。在PSO中,搜索空间的每一个粒子都是优化问题的一个解,每个粒子都有自己的适应度值和速度决定它的距离和方向。PSO从一个随机解出发,通过多次迭代得到最优解。由于PSO具有调整参数较少、运行效率高、易于实现等优点,在函数优化、数据挖掘、神经网络及模糊系统控制等多个领域得到了广泛的应用,并且多种改进算法相继被提出[12-14],但粒子群算法在解决一些实际问题时会出现局部收敛能力较差、易陷入局部最优解的问题,因此该算法的机制需要进一步优化。
近几年来,学者们提出了一系列用于求解TSP的改进离散粒子群算法[15-18]。如:张江维[15]引入变异和利用进化过程信息缩减问题规模等机制,提高了解的精确性,但容易陷入局部最优解;强宁等[16]借鉴力学思想提出一种新的加速度粒子群算法,并设计了基于维度的粒子学习策略和编解码方法,提高解的收敛性和稳定性;Wang等[17]重新定义了粒子的速度和位置,提出了移动算子和移动序列的概念,提高了算法的收敛速度;文献[18]提出了一种基于优秀系数的局部搜索混沌离散粒子群优化算法,给TSP实例中的每段路径设定优秀系数,并在算法机制中添加了混沌序列和局部搜索策略,增强了算法的寻优能力,提高了收敛速度,但静态优秀系数不能根据算法的收敛情况实时更新,对路径的评价具有局限性,可能会导致算法因为保留某段较短路径而不能搜索到全局最优解。为了增强算法的全局搜索能力,对迭代过程中的有用信息进行记录和利用,本文在前面工作[18]的基础上,提出了一种基于自适应优秀系数的粒子群算法(Particle Swarm Optimization algorithm based on Self-adaptive Excellence Coefficient, SECPSO),对原文中的静态优秀系数进行了改进,让其跟随解的变化进行自适应调整,对路径进行更好的评价,从而提高算法全局搜索能力;算法机制中还添加了3-opt搜索策略,提高了算法的局部搜索能力和解的精确性,能更好地求解TSP。
1 研究基础 1.1 旅行商问题的模型旅行商问题的数学描述为给定N座城市以及各城市之间路径的长度,一个旅行商从某个城市出发,遍历所有城市后回到出发点,求一条经过各城市一次且仅一次的最短遍历路线。其形式化描述为:给定一个连通图G(EG, VG),其中EG为顶点(城市)的集合,VG为赋权边(两个城市之间的距离)的集合,问题的目标是确定一条长度最短的Hamilton回路,即遍历所有顶点一次且仅一次的最短回路。
设EG={1, 2, …, H}, VG={(i, j, wij), i, j∈EG, wij∈R+},则Hamilton回路路径为Vk1k2, Vk2k3, …, VkHk1,其中kj∈EG,且
| ${{x}_{ij}}=\left\{ \begin{matrix} 1 & , & \begin{matrix} {} & \begin{matrix} {} & i,j,\text{connected} \\ \end{matrix}\text{ } \\ \end{matrix}\text{ } \\ 0 & , & \begin{matrix} {} & i,j,\text{un-connected} \\ \end{matrix} \\ \end{matrix} \right.$ |
则TSP问题的目标函数是
标准粒子群优化算法中,每个粒子都是优化问题的一个解;粒子根据自身的经验,以及与其他粒子间的信息传递在搜索空间中不断改变自身的飞行速度和方向来搜索问题的最优解。算法利用适应度函数对每个粒子进行评价,并记录下粒子以及整个群体的历史最优位置。
粒子位置用N维向量来表示,设有m个粒子,第i个粒子的位置和速度分别表示为:Xi=(Xi1, Xi2, …, XiN)和Vi=(Vi1, Vi2, …, ViN),其中i=1, 2, …, m。每个粒子的历史最优位置记为pi=(pi1, pi2, …piN),其中∀i(1≤i≤m);整个群体的历史最优位置记为pg=(pg1, pg2, …, pgN)。迭代过程中粒子运动状态可分别由式(1) 及式(2) 来描述:
| ${{\mathit{\boldsymbol{V}}}_{i}}^{t+1}=w{{\mathit{\boldsymbol{V}}}_{i}}^{t}+{{c}_{1}}{{r}_{1}}\left( {{\mathit{\boldsymbol{p}}}_{i}}-{{\mathit{\boldsymbol{X}}}_{i}}^{t} \right)+{{c}_{2}}{{r}_{2}}\left( {{p}_{g}}-{{\mathit{\boldsymbol{X}}}_{i}}^{t} \right)$ | (1) |
| ${{\mathit{\boldsymbol{X}}}_{\bf{i}}}^{t+1}={{\mathit{\boldsymbol{X}}}_{\bf{i}}}^{t}+{{\mathit{\boldsymbol{V}}}_{\bf{i}}}^{t+1}$ | (2) |
其中:i=1, 2, …, m;Vi(t)和Xi(t)分别表示粒子i在t次迭代中的速度和位置;t表示算法当前的迭代次数;w为惯性权重,控制着粒子以前的速度对当前速度的影响,取值在[0,1];c1和c2分别为认知学习率和社会学习率,通常取值为2;r1和r2是两个独立的在区间[0,1]上服从均匀分布的随机数。
1.3 求解TSP的离散粒子群算法利用PSO算法求解离散问题,需要对算法的状态表示和运算规则进行重新定义,扩展传统PSO算法的更新操作,才能实现PSO算法在离散空间的搜索。Clerc[19]针对TSP实例,提出了离散粒子群优化(Discrete Particle Swarm Optimization, DPSO)算法,将粒子位置定义为城市的排列,而速度定义为城市交换的序列,在此基础上,对运算法则也进行了重新定义。
1) 粒子的位置和解空间。
每个粒子的位置向量都表示TSP问题的一个解,设第i个粒子的位置为Xi=(Xi1, Xi2, …, Xin),其中Xi1, Xi2, …, Xin代表n个顶点(城市)的编号,表示从Xi1顶点出发依次经过Xi2,Xi3,…,Xin,最后返回到出发点。
2) 目标函数。
用离散的PSO算法求解TSP,对应的目标函数(即适应度函数)f(Xi)(即为TSP的路径总长度)定义为:
| $f\rm{(}{{\mathit{\boldsymbol{X}}}_{i}}\rm{)}=\sum\limits_{k=1}^{N-1}{{{d}_{ik\rm{(}k+1\rm{)}}}}+{{d}_{1n}}$ | (3) |
目标是求出函数适应度值最小的粒子位置排列,即为TSP所对应的最优解的城市排列。
3) 速度表示。
速度定义为迭代过程中粒子需要进行调整的位置集合,即为TSP中的边的调整集合,是对原来的城市路径进行调整和交换的一个序列。假设速度为V=((a1, a2), (a3, a4), …, (an-1, an)),则(a1, a2)是被最优解选择的排列,在位置调整时保留这个城市排列。借鉴单点调整的思想[20],使用插入法对城市的排序进行改变。如一个城市排列X=(1, 2, 3, 4, 5) ,将速度V=((1, 3) , (2, 5) )作用在X上,找到城市1和城市3的位置,将城市3直接插入到城市1后面,城市排列变为X(1) =(1, 3, 2, 4, 5) ,再继续根据速度序列的第二部分(2, 5) 调整粒子位置,找到城市2和城市5的位置,将城市5插入到城市2的后面,得到最终的城市排列X(2) =(1, 3, 2, 5, 4) 。
4) 更新公式。
对PSO算法进行离散化,运算法则重新定义后,速度和位置的离散迭代公式如下所示:
| $\mathit{\boldsymbol{V}}_{i}^{t+1}=w\otimes \mathit{\boldsymbol{V}}_{i}^{t}\oplus {{r}_{1}}\otimes \left( {{\mathit{\boldsymbol{p}}}_{\rm{best}}}\Theta \mathit{\boldsymbol{X}}_{i}^{t} \right)\oplus {{r}_{2}}\otimes \left( {{\mathit{\boldsymbol{g}}}_{\rm{best}}}\Theta \mathit{\boldsymbol{X}}_{i}^{t} \right)$ | (4) |
| $\mathit{\boldsymbol{X}}_{i}^{t+1}=\mathit{\boldsymbol{X}}_{i}^{t}\oplus \mathit{\boldsymbol{V}}_{i}^{t+1}$ | (5) |
粒子的速度按照式(4) 进行更新,即对城市序列调整序的更新;粒子的位置则按照式(5) 进行更新。由于旅行商问题是离散问题,粒子的位置只能分步依次进行调整,具体调整过程如下:
| $\mathit{\boldsymbol{X}}_{i}^{t+1}\left( 1 \right)={{\mathit{\boldsymbol{X}}}_{i}}^{t}\oplus {{r}_{1}}\otimes \rm{(}{{\mathit{\boldsymbol{p}}}_{\rm{best}}}\Theta {{\mathit{\boldsymbol{X}}}_{i}}^{t}\rm{)}$ | (6) |
| $\mathit{\boldsymbol{X}}_{i}^{t+1}\left( 2 \right)=\mathit{\boldsymbol{X}}_{i}^{t+1}\left( 1 \right)\oplus {{r}_{2}}\otimes \left( {{\mathit{\boldsymbol{g}}}_{\rm{best}}}\Theta \mathit{\boldsymbol{X}}_{i}^{t+1}\left( 1 \right) \right)$ | (7) |
| $\mathit{\boldsymbol{X}}_{i}^{t+1}\left( \rm{3} \right)=\mathit{\boldsymbol{X}}_{i}^{t+1}\left( \rm{2} \right)\oplus w\otimes {{\mathit{\boldsymbol{V}}}_{i}}^{t}$ | (8) |
离散问题与连续优化问题运算法则对应的意义不同,离散PSO算法对运算法则进行了重新定义。运算符定义为原公式里的减号,粒子的最优位置与粒子的当前位置在运算符的作用下,得到一个位置的调整序列,使得当前粒子位置可以通过这个调整序列调整为粒子最优的位置,即粒子的速度。算符定义为原公式里的乘号,概率因子r1,r2与调整序列用作用后,按r1、r2的概率保留速度中的调整序列,得到新的粒子速度即新的位置调整序列;算符⊕定义为调整序列的叠加作用,按照先后顺序对城市的位置进行调整操作。
2 改进3-opt离散粒子群算法求解TSP 2.1 自适应优秀系数基本的离散PSO在解决TSP时收敛速度慢,速度中存在随机项,这样可能会使粒子进入一个自我调整的停滞状态,陷入局部最优解,影响到全局搜索的效率。在之前的工作中为了提高短的边被选中的概率,借鉴轮盘赌选择法的思想,提出了路径优秀系数的概念[18],给每条边都设定一个优秀系数,边(i, j)的优秀系数C的定义如下:
| ${C_{ij}} = \left( {\max (\mathit{\boldsymbol{d}}){\rm{ - }}{d_{ij}}} \right){\rm{/}}\sum {{d_{ij}}} $ | (9) |
| ${{C}_{ij}}=\frac{{{C}^{'}}_{ij}}{\max \rm{(}{{\mathit{\boldsymbol{C}}}^{\bf{'}}}\rm{)}}$ | (10) |
其中:dij为顶点i到顶点j的距离,d为城市之间的距离矩阵,Cij在[0,1]取值。优秀系数的提出大幅度提升了优秀边被留下的概率,同时也降低了距离较长的边被留下的可能,可以充分利用问题领域内的信息,能够提高解的精确性和算法的收敛速度。但本文在后期的研究中发现静态优秀系数无法根据迭代过程中的实时情况进行调整,导致算法在后期只能根据路径的长短判断路径是否优秀,而不能对路径进行综合评价,具有很大的局限性。这可能会导致算法为保留某段较短的路径而产生其他更远的路径连接,无法获得全局最优解,因此本文对静态优秀系数进行了进一步的研究和改进。
为了对迭代过程中的有用信息进行记录和利用,对局部解进一步地挖掘,本文在之前工作的基础上提出了自适应优秀系数的概念,让每一条路径的优秀系数根据在迭代过程中被最优解选中的比例进行自适应动态调整。利用优秀系数的不断更新对算法进行动态评价。自适应优秀系数可以增强算法的探索能力和钻探能力,在每一次迭代过程中对每段路径被最优解选中的次数进行评估,计算它们的选择概率,根据评估的结果决定如何动态调整相应路径的优秀系数。
本算法设置了两个指标index1和index2,它们分别表示某条边在某一次迭代中被m个粒子挑选的次数和未被挑选的次数,显然它们满足index1+index2=m。将两者之比定义为选择概率,并设置阈值参数Limit1和Limit2,以及两个优秀系数权重p1和p2,其中p1<1,p2>1。动态优秀系数的定义如下:
| ${{C}_{ij}}=\left\{ \begin{align} & \begin{matrix} \frac{\max \rm{(}\mathit{\boldsymbol{d}}\rm{)-}{{d}_{ij}}}{\max \rm{(}{{\mathit{\boldsymbol{C}}}^{\bf{'}}}\rm{)}\cdot \sum {{d}_{ij}}}\cdot {{p}_{1}}, & \begin{matrix} {} & \frac{index1}{index2} <Limit1 \\ \end{matrix} \\ \end{matrix} \\ & \begin{matrix} \begin{matrix} \frac{\max \rm{(}\mathit{\boldsymbol{d}}\rm{)-}{{d}_{ij}}}{\max \rm{(}{{\mathit{\boldsymbol{C}}}^{\bf{'}}}\rm{)}\cdot \sum {{d}_{ij}}} & , \\ \end{matrix} & \begin{matrix} {} & Limit2\le \frac{index1}{index2}\le Limit1 \\ \end{matrix} \\ \end{matrix} \\ & \begin{matrix} \frac{\max \rm{(}\mathit{\boldsymbol{d}}\rm{)-}{{d}_{ij}}}{\max \rm{(}{{\mathit{\boldsymbol{C}}}^{\bf{'}}}\rm{)}\centerdot \sum {{d}_{ij}}}\cdot {{p}_{2}}, & \begin{matrix} {} & \frac{index1}{index2}>Limit2 \\ \end{matrix} \\ \end{matrix} \\ \end{align} \right.$ | (11) |
动态优秀系数根据迭代过程中的路径利用率进行实时变化,当某一边的选择概率低于限制参数Limit1时,算法根据优秀系数权重p1降低此条边的优秀系数;当某一边的选择概率高于限制参数Limit2时,算法根据优秀系数权重p2提高此条边的优秀系数;当某一条边的选择概率介于这两者之间,则此条边的优秀系数不变,从而对算法进行动态评价。
添加动态优秀系数后,算法在迭代过程中的更新公式都要发生相应地改变,位置更新公式中的式(6) 、(7) 就可以改为如下形式:
| $\mathit{\boldsymbol{X}}_{i}^{t+1}\left( 1 \right)={{\mathit{\boldsymbol{X}}}_{i}}^{t}\oplus \frac{{{C}_{ij}}\rm{+}{{r}_{1}}}{2}\otimes \rm{(}{{\mathit{\boldsymbol{p}}}_{\rm{best}}}\Theta {{\mathit{\boldsymbol{X}}}_{i}}^{t}\rm{)}$ | (12) |
| $\mathit{\boldsymbol{X}}_{i}^{t+1}\rm{(}2\rm{)}=\mathit{\boldsymbol{X}}_{i}^{t+1}\rm{(}1\rm{)}\oplus \frac{{{C}_{ij}}\rm{+}{{r}_{2}}}{2}\otimes \rm{(}{{\mathit{\boldsymbol{g}}}_{\rm{best}}}\Theta \mathit{\boldsymbol{X}}_{i}^{t+1}\rm{(}1\rm{))}$ | (13) |
自适应优秀系数动态地评价粒子的位置信息,可以充分利用问题领域内的信息,从而提高解的精确性和算法的收敛速度。为了对局部解进一步地挖掘,本文还加入了3-opt局部搜索策略。
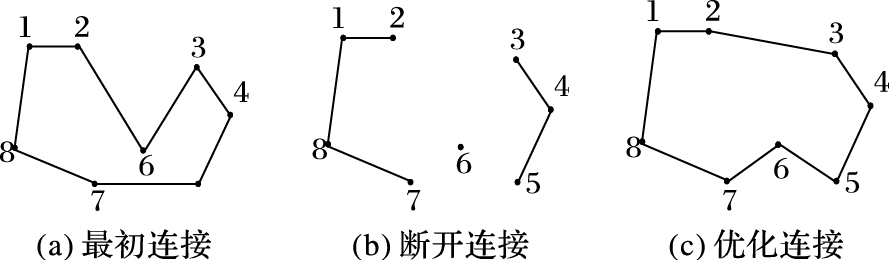
2.2 3-opt局部搜索在优化问题中,3-opt是一种简单的求解TSP的局部搜索算法,加入3-opt交换可以提高解的精确性。3-opt是k-opt算法中的一个特例。如图 1所示,3-opt算法首先要删除一个网络中的3条边, 再尝试重新连接网络的所有其他可能办法, 这个过程涉及到3组不同的连接方式,然后对每次的连接进行评价,选取其中最优的一个。
|
图 1 3-opt的示意图 Figure 1 Schematic diagram of 3-opt |
从图 1可以清晰地看出,图 1(a)是交换前的路径,图 1(b)是断开连接后的状态,如果满足d(2, 3) +d(6, 7) +d(5, 6) <d(2, 6) +d(3, 6) +d(5, 7) ,则接受交换后的路径,如图 1(c)所示,否则恢复原路径。3-opt交换的优点在于仅有被交换的三个边的连接改变了顺序,而其他边的连接情况都没有发生改变,这样极大地减少了检查路径可行性的工作量。
2.3 算法流程自适应优秀系数的粒子群算法求解旅行商问题算法(SECPSO)流程描述如下:
步骤1 算法开始,设置算法所需的参数,如问题规模、粒子数目、迭代次数等;
步骤2 计算算法必需的数据,即每条边的路径长度以及优秀系数;
步骤3 随机产生初始解,即粒子的初始位置和速度并按照式(3) 计算适应度值;
步骤4 判断算法是否达到终止条件;
步骤5 依次按照式(12) 、(13) 、(8) 更新粒子的位置;
步骤6 按照式(11) 更新每段路径的优秀系数;
步骤7 根据3-opt变换对粒子的位置进行局部优化;
步骤8 计算每个粒子的适应度函数值,并与保存的最优值进行比较,若结果更优,则保留并更新粒子最优值,且记录路径,再更新全局的最优值;
步骤9 判断最优值持续不变的次数是否达到:未达到直接返回步骤3;若达到,则程序停止,输出最优解。
3 实验和结果对比分析为了验证改进后的SECPSO算法的性能,本文选取了TSPLIB测试库中的部分案例(数据更新到2013年7月),使用Matlab (R2009b)编程,在CPU为AMD1.65G,RAM为4GB的计算机上进行测试和实验。给出了5种算法在不同城市案例下的求解结果,并对算法的求解结果进行分析和比较,通过实验结果验证算法的有效性。表 1中给出了算法的测试结果,实验设置粒子数为30,最大迭代次数为100,实验测试80次。本文中的实验参数设置为:Limit1=0.4, Limit2=0.5, p1=0.98, p2=1.02, r1=0.4, r2=0.7。
| 表 1 算法的性能测试结果 Table 1 Performance test results of five algorithms |
表 1中的算法分别为基本粒子群算法、基于优秀系数的粒子群算法 (PSO based on Excellence Coefficients, ECPSO)、本文之前的研究工作中提出的改进的局部搜索混沌离散粒子群算法 (Improved Local-search-based Chaotic Discrete Particle Swarm Optimization, ILCDPSO);ILCDPSO+SEC (Self-adaptive Excellence Coefficients)指在ILCDPSO的基础上将静态优秀系数改成自适应优秀系数;SECPSO是本文提出的改进算法。
表 1给出的是算法求解的最优值、平均值、标准差以及平均迭代次数。从表 1中的数据可以看出,ILCDPSO+SEC算法在ILCDPSO的基础上添加了自适应优秀系数后,算法的探索能力进一步加强,搜索范围更广,搜索到的最优值更接近最优解;但算法搜索到的解波动性大,且平均值低于原先算法。与增加了局部搜索策略的ILCDPSO算法相比,添加3-opt搜索策略的算法更好地提高了解的精确性,更接近于已知最优解,且标准差的值也明显降低,这说明算法具有很好的稳定性。本文提出的改进算法结合了3-opt策略和自适应优秀系数,不仅提高了解的精确性,还让算法具有很强的寻优能力并快速地收敛到最优解,算法的标准差也明显低于其他算法,说明SECPSO能够更好地求解TSP。对于规模较大的案例,本文的新算法也能获取到更优的解,由于采用了3-opt策略,使得算法在求解规模较大的案例花费的时间较长,但求解的精度比采用2-opt策略时要好。
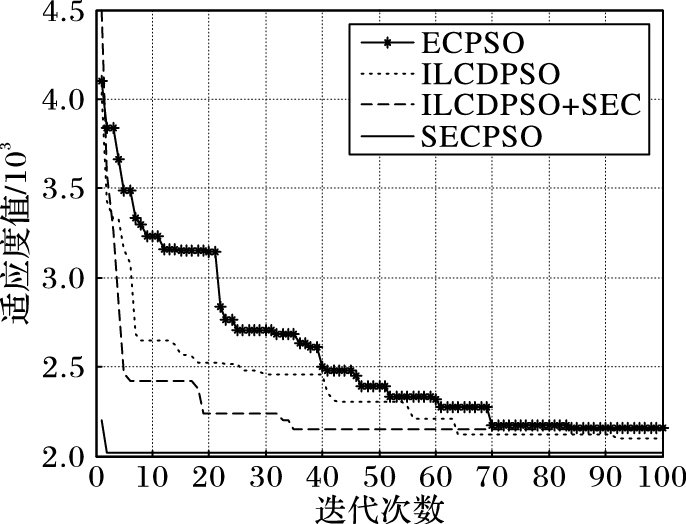
图 1给出了表 1中的五种算法在解决实例Bays29时的收敛曲线图。从图中可以清晰地看出加入3-opt搜索机制后的算法在迭代初期就能够获得比较好的解,并且能快速收敛到最优值。加入了自适应优秀系数的算法相比添加静态优秀系数的算法,收敛速度更快,并能得到更优的解。图 2中也能看出SECPSO的寻优能力和收敛能力都优于其他四种算法。
|
图 2 Bays29实例的不同算法收敛曲线对比 Figure 2 Convergence curve comparison of five algorithms when solving instance Bays29 |
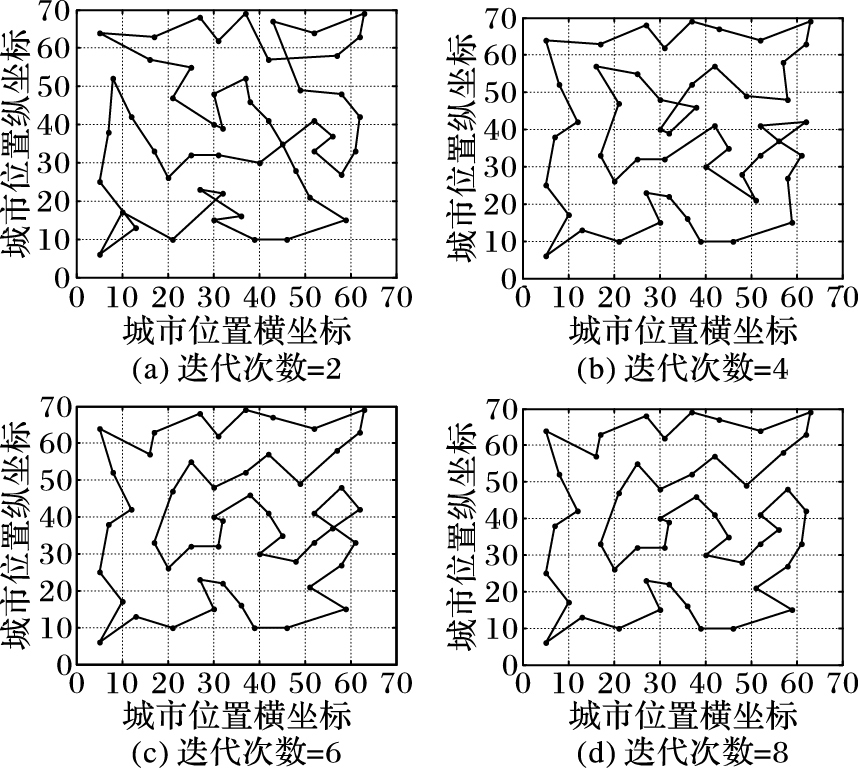
图 3给出的是SECPSO算法在求解实例Eil51时的解的变化过程,分别对应了迭代次数t=2、t=4、t=6以及t=8下的最优解,图 3(a)和3(b)显示算法在快速向最优解靠近,图 3(c)和3(d)反映了算法在求解过程中不断地调整局部位置,防止算法陷入局部最优,直到搜索到最优解为止。
|
图 3 SECPSO算法解决实例Eil51搜索解的变化过程 Figure 3 Process of searching solution of instance Eil51 by SECPSO algorithm |
为了更清晰地看出本算法的优越性,本文将该算法与改进的混沌粒子群优化算法(Improved algorithm of Chaotic Particle Swarm Optimization, ICPSO)[21]进行了性能比较,结果如表 2所示,表中数据的平均解为程序运行30次的平均结果。
| 表 2 SECPSO与ICPSO算法性能比较 Table 2 Performance comparison of SECPSO and ICPSO algorithms |
表 2给出了本文提出的算法与其他文献中的算法的实验比较结果,其中ICPSO是文献[21]中的算法,误差是指算法搜索到的最优解与TSPLIB中给出的已知最优解的相对误差。从表 2中可以清晰看出,本文的算法在最优解的搜索能力上优于ICPSO算法,本文算法得到的最优解更接近已知最优解。虽然在部分实例中,如St70,本文的算法搜索到的最差值比ICPSO要差,但算法平均值都优于它,且误差也明显下降。这说明本文的算法在求解TSP的过程中比ICPSO有较高的寻优能力和钻探能力,算法的性能有了一定的提升。
4 结语为了进一步提高离散粒子群算法的搜索能力,本文在已有的工作基础上进行了改进,提出了一种基于自适应优秀系数的粒子群算法(SECPSO)。改进的策略包括将静态路径优秀系数改成自适应动态优秀系数,及用3-opt变换替换原先算法中的局部搜索策略。SECPSO算法相对ILCDPSO在搜索能力上有了一定的提高,保留了算法原先的优点,即算法在初期保持了粒子位置的随机性,搜索到更多的解;粒子位置调整时保留路径优秀系数较高的边,提高了解的精确性。自适应优秀系数让算法在寻优过程中能够更好地跟随解的搜索情况更新路径的优秀系数,让算法具有很强的寻优能力并快速地达到最优值。实验结果也表明,添加自适应优秀系数,可以提高算法的全局搜索能力,而3-opt搜索策略加快了算法的收敛,提高了算法对最优解的搜索能力。实验结果也验证了两者的结合能够综合提升算法的性能,使得算法在求解TSP时有更好的收敛速度和收敛精度。
| [1] | COOK W J. 迷茫的旅行商:一个无处不在的计算机算法问题[M]. 随春宁,译.北京:人民邮电出版社, 2012:1-278. ( COOK W J. IN Pursuit of the Traveling Salesman:Mathematics at the Limits of Computation[M]. SUI C N, translated. Beijing:Posts & Telecom Press, 2012:1-278. ) |
| [2] | GAREY M R, JOHNSON D S. Computers and Intractability:A Guide to the Theory of NP-Completeness[M]. San Francisco: W.H. Freeman, 1979 : 1 -579. |
| [3] | ROBINSON J B. On the Hamiltonian game (a traveling salesman problem)[J]. Santa Monica, California:RAND Research Memorandum RM-303, 1949 . |
| [4] | BATYRSHIN I, SIDOROV G. Advances in Artificial Intelligence[M]. Berlin: Springer, 2011 : 1 -490. |
| [5] | DORIGO M, MANIEZZO V, COLORNI A. Ant system:optimization by a colony of cooperating Agents[J]. IEEE Transactions on Systems Man & Cybernetics, Part B:Cybernetics, 1996, 26 (1) : 29-41. |
| [6] | KARABOGA D. An idea based on honey bee swarm for numerical optimization, Technical Report-TR06[EB/OL].[2016-02-11]. http://www.rose-hulman.edu/class/se/OldFiles/csse453/schedule/day34/HoneyBeeOptimization.pdf. |
| [7] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ:IEEE, 1995:1942-1948. |
| [8] | KENNEDY J, EBERHART R. A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science. Piscataway, NJ:IEEE, 1995:39-43. |
| [9] | 刘朝华, 张英杰, 章兢, 等. 蚁群算法与免疫算法的融合及其在TSP中的应用[J]. 控制与决策, 2010, 25 (5) : 695-700. ( LIU C H, ZHANG Y J, ZHANG J, et al. Using combination of ant algorithm and immune algorithm to solve TSP[J]. Control and Decision, 2010, 25 (5) : 695-700. ) |
| [10] | 刘朝华, 张英杰, 李小花, 等. 双态免疫优势蚁群算法及其在TSP中的应用研究[J]. 小型微型计算机系统, 2010, 31 (5) : 937-941. ( LIU C H, ZHANG Y J, LI X H, et al. Research of using binary state ACA based on immune dominance to solve TSP[J]. Journal of Chinese Computer Systems, 2010, 31 (5) : 937-941. ) |
| [11] | 姚明海, 王娜, 赵连朋. 改进的模拟退火和遗传算法求解TSP问题[J]. 计算机工程与应用, 2013, 49 (14) : 60-65. ( YAO M H, WANG N, ZHAO L P. Improved simulated annealing algorithm and genetic algorithm for TSP[J]. Computer Engineering and Applications, 2013, 49 (14) : 60-65. ) |
| [12] | LU H, CHEN W. Dynamic-objective particle swarm optimization for constrained optimization problems[J]. Journal of Combination Optimization, 2006, 12 (4) : 409-419. doi: 10.1007/s10878-006-9004-x |
| [13] | LU H, CHEN W. Self-adaptive velocity particle swarm optimization for solving constrained optimization problems[J]. Journal of Global Optimization, 2008, 41 (3) : 427-445. doi: 10.1007/s10898-007-9255-9 |
| [14] | 徐向平, 鲁海燕, 徐迅. 基于环形邻域的混沌粒子群聚类算法[J]. 计算机工程与应用, 2016, 52 (2) : 54-60. ( XU X P, LU H Y, XU X. Ring neighborhood based chaotic particle swarm optimization algorithm for clustering[J]. Computer Engineering and Applications, 2016, 52 (2) : 54-60. ) |
| [15] | 张江维. 自适应混合粒子群优化算法求解大规模旅行商问题[J]. 计算机应用与软件, 2015, 32 (12) : 265-269. ( ZHANG J W. Solving large-scale TSP with adaptive hybrid PSO[J]. Computer Applications and Software, 2015, 32 (12) : 265-269. ) |
| [16] | 强宁, 康凤举. 加速度粒子群算法在多旅行商问题中的应用[J]. 陕西师范大学学报(自然科学版), 2015, 43 (6) : 36-42. ( QIANG N, KANG F J. Application of a new acceleration particle swarm optimization for solving multiple traveling salesman problem[J]. Journal of Shaanxi Normal University (Nature Science Edition), 2015, 43 (6) : 36-42. ) |
| [17] | WANG X, MU A, ZHU S. ISPO:a new way to solve traveling salesman problem[J]. Intelligent Control and Automation, 2013, 4 (2) : 122-125. doi: 10.4236/ica.2013.42017 |
| [18] | 程毕芸, 鲁海燕, 徐向平, 等. 求解旅行商问题的改进局部搜索混沌离散粒子群优化算法[J]. 计算机应用, 2016, 36 (1) : 138-142. ( CHENG B Y, LU H Y, XU X P, et al. Improved local-search-based chaotic discrete particle swarm optimization algorithm for solving traveling salesman problem[J]. Journal of Computer Applications, 2016, 36 (1) : 138-142. ) |
| [19] | CLERC M. Discrete particle swarm optimization, illustrated by the traveling salesman problem[M]. Berlin: Springer, 2004 : 219 -239. |
| [20] | 刘任任. 算法分析与设计[M]. 武汉: 武汉理工大学出版社, 2003 : 1 -155. ( LIU R R. Algorithm Analysis and Design[M]. Wuhan: Wuhan University of Technology Press, 2003 : 1 -155. ) |
| [21] | 李文, 伍铁斌, 赵全友, 等. 改进的混沌粒子群算法在TSP中的应用[J]. 计算机应用研究, 2015, 32 (7) : 2065-2067. ( LI W, WU T B, ZHAO Q Y, et al. Improved algorithm of chaotic particle swarm and its application in TSP[J]. Application Research of Computers, 2015, 32 (7) : 2065-2067. ) |




