支持向量回归是建立在统计学习理论基础上的一种机器学习方法[1],近年来由于机器学习的热潮,得到了广泛应用。传统支持向量回归算法在处理具有多输出问题时通常采用针对单输出构造回归模型,未考虑到输出变量之间相关性,影响预测精度和收敛速度,因此,构建具有多输出支持向量回归算法具有重要的意义。文献[2-4]介绍了多输出支持向量回归算法在解决实际问题中的表现。
支持向量回归求解的问题最终都将转化成最优化问题,而最优化问题中无约束优化问题[5-6]涉及的数学模型更多、更容易求解、解法可以应用于有约束最优化问题,因而得到更广泛的研究与应用。无约束最优化问题的求解方法有很多种,主要有递推下降法、牛顿法、修正牛顿法、共轭梯度法和拟牛顿法[7]。递推下降法结构简单、计算量小,但具有一阶收敛速度且依赖于初始值及步长的选取,靠近极值点时容易产生局部震荡;牛顿法及其改进牛顿法虽然具有二阶收敛速度,但在迭代过程中每一次构造搜索方向时需要先计算目标函数的Hessian矩阵,再去求解线性方程组,计算量大且在Hessian矩阵不正定时不能产生正确的下降方向作为算法的迭代方向;共轭梯度法虽然计算简单,收敛速度也比递推下降法提高了很多,但是全局收敛性无法得到保证;因此使用近似Hessian矩阵计算迭代方向的拟牛顿算法[8]自提出以来就被广泛的研究,是目前求解无约束最优化问题最成熟有效的解法之一,因此,本文研究修正的拟牛顿法结合非精确线搜索技术解决多输出数据依赖核支持向量回归算法。
1 多输出数据依赖核SVR算法 1.1 多输出支持向量回归算法多输出支持向量回归(Multidimensional Support Vector Regression, MSVR)[9]是将单输出推广到多输出。假设给定样本数据:
| $T=\{({{x}_{i}},\rm{ }{{y}_{i}})|{{x}_{i}}\in {{\mathit{\boldsymbol{R}}}^{n}},\rm{ }{{y}_{i}}\in {{\mathit{\boldsymbol{R}}}^{m}},\rm{ }i=1,\rm{ }2,\rm{ }\ldots ,\rm{ }l\}$ | (1) |
建立输入数据与输出数据之间的回归函数:
| $f({{x}_{i}})=W\cdot \varphi ({{x}^{i}})+\mathit{\boldsymbol{B}}$ | (2) |
其中:φ(xi)中表示非线性映射函数,W是由权向量构成的行列式,W=[w1T, w2T, …,wnT]T∈Rm×n,B是由实数构成的向量,B=[b1, b2, …,bn]T∈Rn。
由最小化经验风险和输出误差原则,将MSVR问题直接转化为二次规划问题:
| $\begin{array}{*{35}{l}} \rm{min}\sum\limits_{j=1}^{n}{{}}\|{{w}_{j}}{{\|}^{2}}+C\sum\limits_{j=1}^{l}{{}}\xi _{i}^{2} \\ \rm{s}\rm{.t}.\|{{y}_{i}}-\mathit{\boldsymbol{W}}\cdot \varphi \left( {{x}_{i}} \right)-\mathit{\boldsymbol{B}}\|\le \varepsilon +{{\xi }_{i}};\rm{ }{{\xi }_{i}}\ge 0 \\ \end{array}$ | (3) |
其中:ξi是xi的松弛变量,C为惩罚因子。由于式(3) 中的不等式约束条件不是仿射函数,引入定义在超球面上的ε二次不敏感损失函数:
| $L\varepsilon \left( z \right)=\left\{ \begin{align} & 0, & z <\varepsilon \\ & {{(z-\varepsilon )}^{2}}, & z\ge \varepsilon \\ \end{align} \right.$ | (4) |
将式(4) 代入式(3) 可将MSVR转化为无约束最优化问题:
| ${\rm{min}}\sum\limits_{j = 1}^n {{{\left\| {{\mathit{\boldsymbol{w}}_j}} \right\|}^2}} + C\sum\limits_{j = 1}^l {{L_\varepsilon }} (\left\| {{\mathit{\boldsymbol{y}}_i} - \mathit{\boldsymbol{W}} \times \varphi ({x_i}) - \mathit{\boldsymbol{B}}} \right\|)$ | (5) |
式(5) 中目标函数对自变量W和B来说是凸函数,因此可直接对wj求偏导,其表达式值为0时得到的解就是回归问题的最优解wj*。
由于引入了超球面上的二次不敏感损失函数,在wj*的求解过程中,与单输入支持向量回归不同,MSVR多采用迭代的方法进行求解,如递推下降法、牛顿法、拟牛顿法等,主要思想是根据已有的wk*和Bk来求解下一个wk+1*和Bk+1。
1.2 数据依赖核函数针对MSVR问题引入数据依赖核方法[10]优化模型参数,相对于传统核优化算法,数据依赖核方法能够改变原始数据在映射空间的几何结构,因此具有更好的表现。
通常人们根据问题和样本数据的不同,多靠经验选择不同的核函数。常用的核函数有多项式核、高斯核和线性核等,但这些核函数对于不同的样本数据都是固定的,并未考虑到实际数据中的噪声等干扰,因此根据具体数据构造相应的核函数在参数优化过程中能够有更好的表现。
由Amari等[11]提出的数据依赖核通过修改空间几何结构中的内核方法来提高核函数效果,同时提出共形变换c(x),对传统核函数进行保角变换,确保数据间的角度在映射空间不会发生变化,得到如下公式:
| $\tilde{K}(x,{x}')=c(x)c({x}')K(x,{x}')$ | (6) |
其中:c(x)为关于x的正定函数,$\tilde k$(x, x′)为满足Mercer条件的数据依赖核函数。
1.3 基于数据依赖核的MSVR模型由1.1节推导可知,MSVR算法的求解主要在于解决模型中W和B参数。通过对式(5) 求偏导并令其导数为0可得函数:
| $L({{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}})=\lambda \mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }_{\rm{aug}}^{T}{{\mathit{\boldsymbol{K}}}_{\rm{aug}}}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}}+\sum\limits_{i=1}^{n}{{{L}_{\varepsilon }}}(\left\| {{\mathit{\boldsymbol{y}}}_{i}}-\mathit{\boldsymbol{K}}_{i}^{T}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}} \right\|)$ | (7) |
其中 βaug为简化函数的自定义变量,定义:
| ${{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{i,j}}=-\frac{2}{C}\cdot \frac{\partial }{\partial {{w}_{j}}}{{L}_{\varepsilon }}(||{{y}_{i}}-\mathit{\boldsymbol{W}}\cdot \phi ({{\bf{x}}_{i}})-\mathit{\boldsymbol{B}}||)$ | (8) |
由式(8) 可得:
| $\left\{ \begin{align} & L({{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}})=\lambda \mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }_{\rm{aug}}^{\rm{T}}{{\mathit{\boldsymbol{K}}}_{\rm{aug}}}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}}+\sum\limits_{i=1}^{n}{{{L}_{\varepsilon }}}(\left\| {{y}_{i}}-\mathit{\boldsymbol{K}}_{i}^{T}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}} \right\|) \\ & {{W}_{j}}=\sum\limits_{i=1}^{n}{\Phi ({{x}_{i}})\beta _{j}^{i}} \\ \end{align} \right.$ | (9) |
求解过程转化为对β的求解,为了得到等式(7) 的最小值,采用牛顿迭代法进行递归求解β。由牛顿法的迭代公式:
| $\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }_{\rm{aug}}^{\rm{new}}\rm{=}\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }_{\rm{aug}}^{\rm{old}}\rm{-}\alpha {{\bf{H}}^{\rm{-1}}}\bf{G}$ | (10) |
其中:H为函数关于β的一阶导数,G为函数关于β的二阶导数,α为函数迭代过程中的步长因子。最后将式(6) 代表的数据依赖核函数代入式(7) , 可得最终的模型:
| $L({{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}})=\lambda \mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }_{\rm{aug}}^{\rm{T}}{{K}_{\rm{aug}}}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}}+{{\sum\limits_{i=1}^{M\rm{s}v}{(\left\| {{y}_{i}}-K_{i}^{T}{{\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }}_{\rm{aug}}} \right\|-\varepsilon )}}^{2}}$ | (11) |
对式(11) 求解,满足‖yi-KiTβaug‖>ε的点即为支持向量点。最后通过求解的βi来计算原始模参数W和B,得到最终的回归模型。
2 快速学习算法 2.1 基于数据依赖核的MSVR最优化算法基于数据依赖核的MSVR问题最终转化为无约束最优化问题的求解。通常采用迭代的方法求其最优解,其基本思想是:给定一个初始点,按照指定的迭代规则生成一个点列,使得该点列是有穷点列时,其最后一个点是最优化模型的最优解;当该点列是无穷点列时,它有极值,且极值点是最优化模型问题的最优解。在求解过程中,选择好初始点后,要选择方向和步长。方向由迭代算法确定,如递推下降法dk=-gk、牛顿法dk=-Gk-1gk、拟牛顿法dk=-Hkgk等,其中Gk为目标函数的Hessian矩阵,gk为目标函数的一阶导数,Hk为Hessian矩阵的近似矩阵。通过迭代方法确定好搜索方向后,需要确定从当前点xk处沿着该方向走多远来到达下一个迭代点,过大或者过小的步长都会使迭代收敛速度变慢,甚至有可能使算法发散,通常采用线搜索技术确定迭代过程中的步长来保证最终形成的迭代序列收敛。
2.2 Armijo准则确定步长线搜索技术分为精确线搜索和非精确线搜索,主要区别在于步长的确定方式。对于非精确线搜索,只需要保证步长αk使得目标函数得到可接受的下降量,即:
| $\Delta {{f}_{k}}=f({{x}_{k}})-f({{x}_{k}}+{{\alpha }_{k}}{{d}_{k}})>0$ | (12) |
就能使最终的迭代序列收敛,其中Armijo准则是一种不需要计算较多函数值和梯度值的非精确线搜索算法。
Armijo准则 已知当前迭代点xk和迭代的方向dk,给定β∈(0, 0.5) ,σ∈(ρ, 1) 。令步长因子αk=βmk,其中mk为满足式(13) 的最小非负整数。
| $f({{x}_{k}}+{{\beta }^{m}}{{d}_{k}})\le f({{x}_{k}})+\delta {{\beta }^{m}}{{g}_{k}}^{T}{{d}_{k}}$ | (13) |
由式(13) 可确定下一个迭代点xk+1=xk+αdk。
2.3 拟牛顿法选择迭代方向 2.3.1 经典牛顿法牛顿法利用目标函数的二阶导数信息,用二次曲面拟合局部曲面,具有二阶收敛速度。其基本思想是用迭代点xk处的一阶导数gk和二阶导数Gk对目标函数进行二次近似,然后把二次模型的极小点作为新的迭代点,其推导过程如式(14) ~(16) 。
将目标函数f(x)在xk处进行二次Taylor展开:
| $T(f,{{x}_{k}},3)={{f}_{k}}+{{g}_{K}}^{T}(x-{{x}_{k}})+\frac{1}{2}{{(x-{{x}_{k}})}^{T}}{{G}_{k}}(x-{{x}_{k}})$ | (14) |
对x求导,令其导数为0求其稳定:点
| $\nabla T={{g}_{k}}+G{}_{k}(x-{{x}_{k}})=0$ | (15) |
当Hessian矩阵Gk非奇异时, 式(15) 可求解,其解为式(16) 所示:
| ${{x}_{k+1}}={{x}_{k}}-{{G}_{k}}^{-1}{{g}_{k}}$ | (16) |
式(16) 即为牛顿法的迭代公式。
由上述推导过程可以看出牛顿法在求解过程中需要存储二阶导数信息和计算目标函数的Hessian矩阵,且无法保证Hessian矩阵在迭代的过程中始终处于正定状态,所产生的方向就不一定是目标函数在xk处的下降方向。
2.3.2 修正的BFGS算法牛顿法计算Hessian矩阵工作量大,并且目标函数的Hessian矩阵不一定存在,因此利用目标函数f和其一阶导数信息构造目标函数的曲率近似的拟牛顿法[12]在解决实际问题中收敛速度更快。近似牛顿法的基本思想是用Hessian矩阵Gk的某个近似矩阵Bk取代Gk,使算法产生的方向近似于牛顿方向。
对式(14) 求导,得g(x)≈gk+1+Gk+1(x-xk+1),令x=xk, sk=xk+1-xk, yk=gk+1-gk,则有:
| ${{\mathit{\boldsymbol{G}}}_{k+1}}{{\mathit{\boldsymbol{s}}}_{k}}\approx \mathit{\boldsymbol{y}}{}_{k}$ | (17) |
用近似矩阵Bk代替Hessian矩阵可得拟牛顿方程Bk+1sk=yk,因此搜索方向可由dk=-Hkgk确定(H为矩阵B的逆),Bk被称为校正规则。
拟牛顿法的关键在于选择合适的校正规则。实验发现,基于秩2校正规则的修正BFGS算法在MSVR模型参数拟合过程中具有更好的表现。对于Armijo搜索准则来说,不能满足当skTyk>0时,Bk正定,则Bk+1也正定。修正的更新公式为:
| ${{\mathit{\boldsymbol{B}}}_{k+1}}=\left\{ \begin{align} & {{\mathit{\boldsymbol{B}}}_{k}}\begin{matrix} {} & {} & {} & \mathit{\boldsymbol{s}}_{k}^{T}{{\mathit{\boldsymbol{y}}}_{k}}\le 0 \\ \end{matrix} \\ & {{\mathit{\boldsymbol{B}}}_{k}}-\frac{{{\mathit{\boldsymbol{B}}}_{k}}{{\mathit{\boldsymbol{y}}}_{k}}\mathit{\boldsymbol{y}}_{k}^{T}{{\mathit{\boldsymbol{B}}}_{k}}}{y_{k}^{T}{{\mathit{\boldsymbol{B}}}_{k}}{{\mathit{\boldsymbol{y}}}_{k}}}+\frac{{{\mathit{\boldsymbol{s}}}_{k}}\mathit{\boldsymbol{s}}_{k}^{T}}{\mathit{\boldsymbol{s}}_{k}^{T}{{\mathit{\boldsymbol{y}}}_{k}}},\begin{matrix} {} & \mathit{\boldsymbol{s}}_{k}^{T}{{\mathit{\boldsymbol{y}}}_{k}}>0 \\ \end{matrix} \\ \end{align} \right.$ | (18) |
结合Armijo准则,算法迭代过程如下:
步骤1 给定参数δ∈(0, 1) , σ∈(0, 0.5) ,初始点x0∈R,终止误差0≤ε<1。初始对称正定矩阵H0(通常取G(x0)-1或单位阵In)。令k←0;
步骤2 计算gk=∇f(xk)。若‖gk‖≤ε,停止迭代,输出x*≈xk;
步骤3 计算搜索方向dk=-Hkgk;
步骤4 记mk是满足式(13) 的最小非负整数m;
步骤5 由上式校正公式确定Hk+1;
步骤6 k←k+1,转步骤2。
2.4 算法在MSVR-DDK模型中的应用将修正的BFGS算法应用到MSVR,结合Armijo准则确定搜索步长,多输出数据依赖核支持向量回归模型参数拟合过程如下:
步骤1 初始化β、δ、σ和H0,根据输入样本与数据依赖核函数计算K;
步骤2 计算‖yi-KiTβaug‖>ε的点,找出支持向量;
步骤3 将训练集重新排序,所有支持向量点前置;
步骤4 计算一阶偏导gk,若‖gk‖≤ε,停止迭代,输出βk;
步骤5 计算步长和搜索方向dk=-Hkgk;
步骤6 计算βk+1,βk+1=βk-αH-1G。
步骤7 由校正公式更新Hk+1,返回步骤2。
3 仿真实验考虑到多输出数据依赖核模型的输入数据之间的关联性,采用相互关联模型式(19) 构造样本数据:
| $\left\{ \begin{array}{l} {y_1} = \sin (3x) + cos(10x)\\ {y_2} = \sin ({y_1}/5) + cos({y_1}/2) \end{array} \right.$ | (19) |
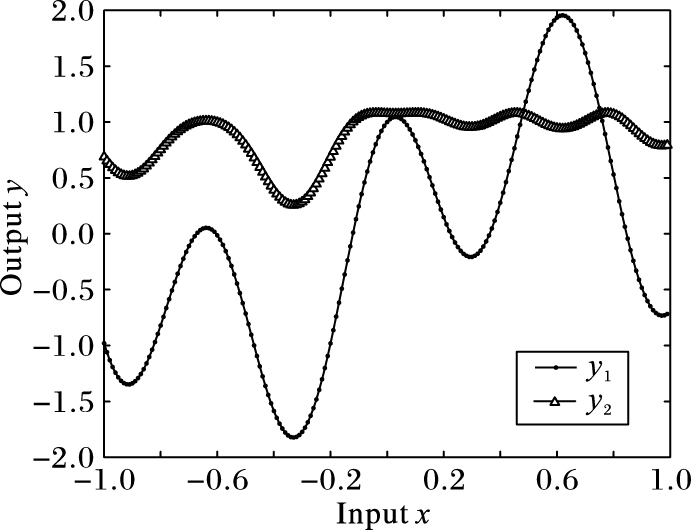
其中:x为样本的输入,y1、y2为相互关联的二维输出。以0.01为间隔,根据式(19) 从-1到1共产生200个样本点。其中前150个点作为训练数据,后50个点作为测试数据,选取C为10,ε为0.1。样本数据的分布如图 1所示。
|
图 1 MSVR-DDK的样本数据分布 Figure 1 Sample data distribution of MSVR-DDK |
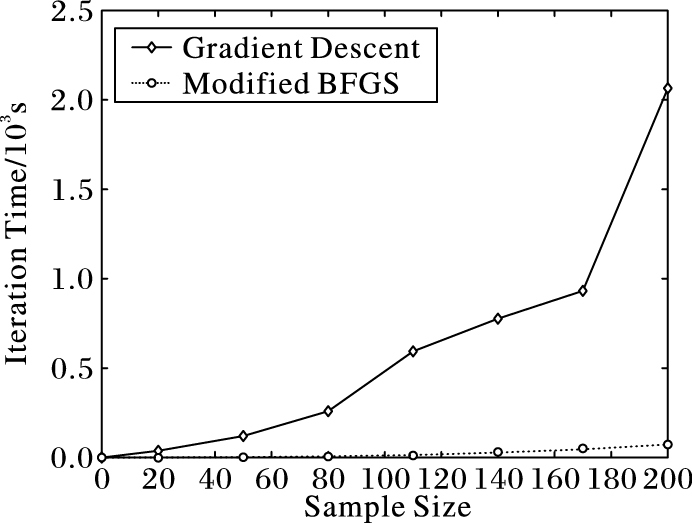
利用MSVR算法针对样本数据建立模型,分别选取不同的初始核函数优化数据依赖核函数生成基于数据依赖核的多输出支持向量回归(Multi-output Support Vector Regression with Data-Dependent Kernel, MSVR-DDK)模型。最后分别使用递推下降法、牛顿法、修正的拟牛顿法进行模型参数的拟合,并比较算法的迭代时间。比较结果如图 2、3所示。
|
图 2 修正BFGS算法与梯度下降法迭代时间比较 Figure 2 Iteration time comparison between modified BFGS algorithm and gradient descent method |
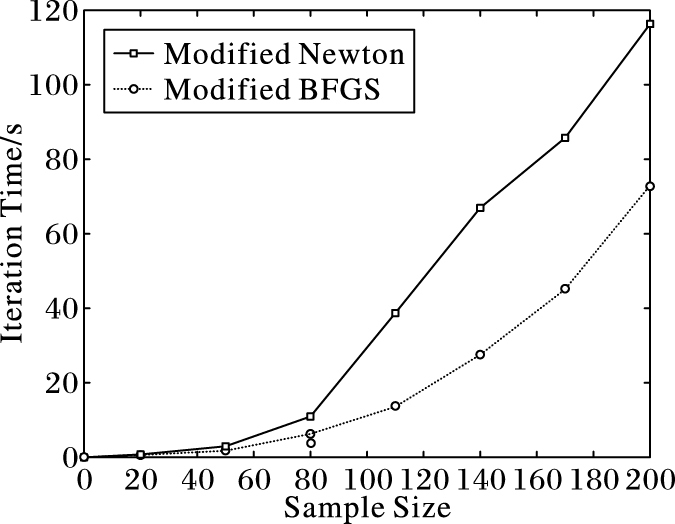
|
图 3 修正BFGS算法与修正牛顿法迭代时间比较 Figure 3 Iteration time comparison between modified BFGS algorithm and modified Newton method |
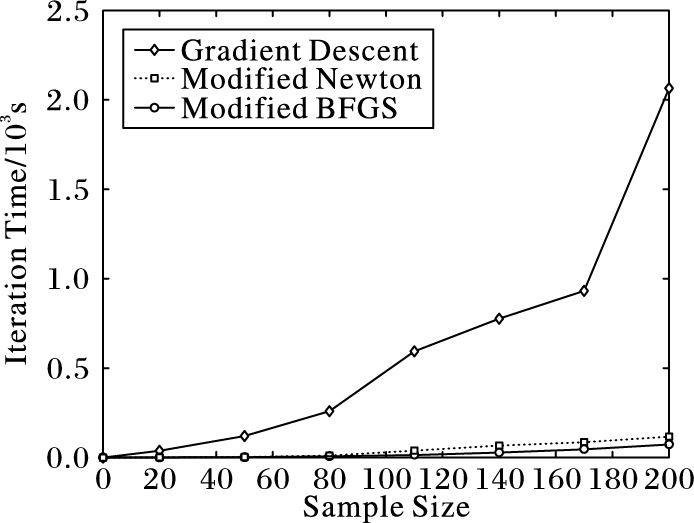
经典牛顿法并不能保证在迭代过程中目标函数的Hessian矩阵都是正定的,因此确定的优化方向并不一定是下降方向,且在Hessian矩阵奇异时算法无法进行下去。为了保证实验结果具有可对比性,迭代过程中对牛顿法进行了修正,修正思想为:在Hessian矩阵正定时,采用牛顿法计算优化方向,否则采用负梯度方向作为优化方向,保证了牛顿法在迭代过程中最终能够收敛。由图 2和图 3可知,在选用多项式核作为数据依赖核的初始核函数进行样本训练时,梯度下降法的迭代时间是修正牛顿法和修正BFGS算法的数十倍,修正的BFGS算法与修正牛顿法在样本数目较少的情况下迭代时间相差不大,但是随着样本数据增多时间差距被逐渐放大。图 4给出三个算法的对比结果。
|
图 4 梯度下降法、修正BFGS算法与修正牛顿法对比 Figure 4 Iteration time comparison of gradient descent method, modified BFGS and modified Newton method |
由图 4可知,修正的BFGS算法在多输出数据依赖核支持向量回归算法的迭代过程中具有最短的迭代时间。
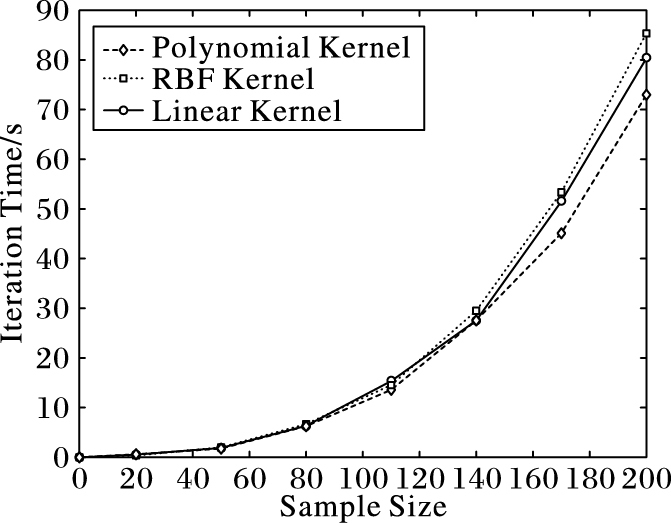
为进一步提升算法的效率,分别采用多项式核、线性核、RBF核作为数据依赖核函数的初始核函数,比较BFGS算法的实验结果,如图 5所示。
由图 5可以看出,选取多项式核作为初始核函数可使算法获得更少的迭代时间。
|
图 5 修正BFGS算法在不同核函数下的迭代时间 Figure 5 Iteration time of modified BFGS algorithm under different kernel functions |
为了定量评价实验结果,定义样本迭代速率SIR:
| $SIR=N/t$ | (20) |
其中,t为算法的迭代时间;N为迭代时样本的数目。三种方法的迭代时间如表 1所示。
| 表 1 三种算法的迭代时间和迭代速率对比 Table 1 Comparison of iteration time and iteration speed of three algorithms |
从表 1的迭代时间可以看出,在200个样本时,修正的BFGS算法迭代时间只有72.98s,明显少于梯度下降法的2065.22s和修正牛顿法的116.34s,具有较好的表现。
表 1的迭代速率为使用式(20) 定义的公式对比三种算法在不同样本数目时的迭代速率。
从表 1的迭代速率可以看出,在200个样本时,修正的BFGS算法收敛速率明显大于梯度下降法与牛顿法,因此证明了算法在模型中的有效性。
4 结语多输出数据依赖核支持向量回归结合非精确线搜索技术(Armijo准则)将秩2校正公式的修正BFGS迭代算法应用于模型参数拟合,同时将模型与基于递推下降法、修正牛顿法拟合的MSVR模型预测结果进行实验分析,实验结果表明,修正的BFGS迭代算法在模型参数拟合过程中具有更快的收敛速度。
| [1] | VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995 : 280 -292. |
| [2] | 王定成, 倪郁佳, 陈北京, 等. 基于数据依赖核支持向量机回归的风速预测模型[J]. 南京师大学报(自然科学版), 2014, 37 (3) : 15-20. ( WANG D C, NI Y J, CHEN B J, et al. A wind speed forecasting model based on support vector regression with data dependent kernel[J]. Journal of Nanjing Normal University (Natural Science Edition), 2014, 37 (3) : 15-20. ) |
| [3] | YANG Y, CHEN D, DONG Z. Novel multi-output support vector regression model via double regularization[C]//Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, NJ:IEEE, 2015:2697-2701. |
| [4] | GAO F, TANG Y, LUO L. Nonlinear correction for thermocouple vacuum sensor based on multiple support vector regressions[C]//Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation. Washington, DC:IEEE Computer Society, 2010, 2:781-784. |
| [5] | 李兵.支持向量机的迭代学习算法及其应用[D].北京:清华大学,2014. ( LI B. Iterative training algorithms of support vector machines and applications[D]. Beijing:Tsinghua University, 2014. ) |
| [6] | 屈晓军.非凸无约束优化问题的修正拟牛顿算法[D].长沙:湖南大学,2014. ( QU X J. The modified quasi-Newton method for nonconvex unconstrained optimization problems[D]. Changsha:Hunan University, 2014. ) |
| [7] | 赖炎连. 优化问题的拟牛顿算法[J]. 咸宁师专学报, 2001, 21 (6) : 1-7. ( LAI Y L. Quasi-Newton methods for the optimization problem[J]. Journal of Xianning Teachers College, 2001, 21 (6) : 1-7. ) |
| [8] | 白华.一类新拟牛顿算法及其收敛性[D].南京:南京理工大学,2006. ( BAI H. A new Quasi-Newton method and its convergence[D]. Nanjing:Nanjing University of Science and Technology, 2006. ) |
| [9] | WANG D, NI Y, CHEN B, et al. Wind speed and direction predictions based on multidimensional support vector regression with data-dependent kernel[M]. Berlin: Springer, 2015 : 427 -436. |
| [10] | 李君宝, 高会军. 基于数据依赖核函数的核优化算法[J]. 模式识别与人工智能, 2010, 23 (3) : 300-306. ( LI J B. Data-dependent kernel function based kernel optimization algorithm[J]. Pattern Recognition and Artificial Intelligence, 2010, 23 (3) : 300-306. ) |
| [11] | AMARI S, WU S. Improving support vector machine classifiers by modifying kernel functions[J]. Neural Networks, 1999, 12 (6) : 783-789. doi: 10.1016/S0893-6080(99)00032-5 |
| [12] | MOKHTARI A, RIBEIRO A. Regularized stochastic BFGS algorithm[J]. IEEE Transactions on Signal Processing, 2014, 62 (23) : 6089-6104. doi: 10.1109/TSP.2014.2357775 |




