2. 广东科学技术职业学院 计算机工程技术学院, 广东 珠海 519090;
3. 东莞理工大学 计算机学院, 广东 东莞 523808;
4. 惠州学院 教育技术中心, 广东 惠州 516007
2. Computer Engineering Technical College, Guangdong Polytechnic of Science and Technology, Zhuhai Guangdong 519090, China;
3. Computer Institute, Dongguan University of Technology, Dongguan Guangdong 523808, China;
4. Educational Technology Center, Huizhou University, Huizhou Guangdong 516007, China
蚁群优化(Ant Colony Optimization, ACO)算法是智能优化应用中的经典算法之一,最早由意大利学者Dorigo等在20世纪90年代提出。原始蚁群算法并不能直接应用于路由寻优,在对该算法进行改进后,可以用于求解多约束服务质量路由(Quality of Service Routing, QoSR)问题。由于QoSR本身是一个难以处理的NP完全(Non-deterministic Polynomial Complete, NP-C)问题[1],因此改进蚁群算法求解QoSR问题一直以来都是学者研究的热点和难点。 Stützle等[2]提出一种最大最小蚁群系统(Max-Min Ant System, MMAS),是一种经典的组合优化算法。MMAS算法的优点是防止过早的停滞现象,寻求全局最优解,但该算法需要将信息素限制在[τmax, τmin],然而τmax和τmin的取值不太容易界定,取值不当反而难以解决局部最优问题,且该算法的收敛速度并不理想。杨洁等[3]提出一种基于信息素强度的蚁群算法,该算法在选择路径时只考虑信息素强度,但信息素强度的初始化和更新结合了路径长度这一因素。文献[4]借助相遇搜索策略对传统蚁群算法进行了改进,将各条寻优路径上的残留信息数限定在一个特定区间,使得改进算法能够相对迅速地收敛。文献[5]在状态转移规则和信息素更新两方面对传统蚁群算法作了部分改进(简称为叶华乔蚁群算法),能够一定程度解决蚁群算法收敛速度慢的问题,但以上蚁群算法的改进重点是收敛速度,而非收敛结果,且以上几种改进蚁群算法的实验模型相对简单,缺乏复杂实验的证明。王宏霞等[6]提出一种量子蚁群算法,该算法针对QoS路由特性对量子蚁群进行了改进,在一定程度上克服了易陷入局部最优的问题,但算法的复杂度有些偏高。文献[7-8]将蚁群算法同免疫算法相融合,有效抑制了蚁群的局部最优问题,缺点同样是增加了算法的复杂度,且没有对改进算法的稳定性进行分析。邢志娟[9]提出一种适用于多目标优化问题的改进蚁群算法,该算法对初始蚁群中处于可行解位置的每只蚂蚁添加一个比较小的随机扰动值,以降低陷入局部最优解的可能性。该算法的改进思想有借鉴作用,但随机扰动值的取值范围较为粗略,作者并没有对随机扰动值如何取值进行深入的理论分析。王永[10]提出一种基于云模型的多目标蚁群算法(Cloud-based Multi-objective Ant Colony Algorithm, CMACA),通过引入云模型次支配解模糊判定机制,找出次支配解,增加蚁群的搜索空间,提高QoSR寻优过程中可行解的多样性。仿真实验结果显示CMACA的Pareto最优解分布更加均匀,但该算法并未对收敛速度进行分析。王健安[11]提出一种基于蚁群优化算法的分布式多约束QoSR算法,将参数自适应策略与最大最小蚂蚁的改进策略结合起来实现对基本蚁群算法的改进,但仿真实验环境较为简单,且并未对算法的收敛速度进行分析。
综上所述,目前多数改进蚁群算法求解QoSR问题仍然存在局部最优以及收敛速度过慢的问题[12],并且改进算法自身的稳定性也较少有人进行研究。为解决以上问题,本文提出一种引入梯度下降的蚁群算法(Ant Colony Algorithm with Gradient Descent, ACAGD),将梯度下降法引入到蚁群算法的局部搜索中,结合残余信息素,综合影响决定蚂蚁的下一跳选择行为策略。蚂蚁不仅以一定概率pi按照信息素浓度搜索下一跳,还以一定概率1-pi按照梯度下降法搜索下一跳,从而降低传统蚁群算法容易陷入局部最优的可能性,得到较优的收敛结果。本文对改进蚁群算法的参数取值进行了实验分析,在一定的参数条件下,ACAGD能够在收敛速度不受影响的情况下取得综合代价相对较低的路由,且算法的稳定性较好。
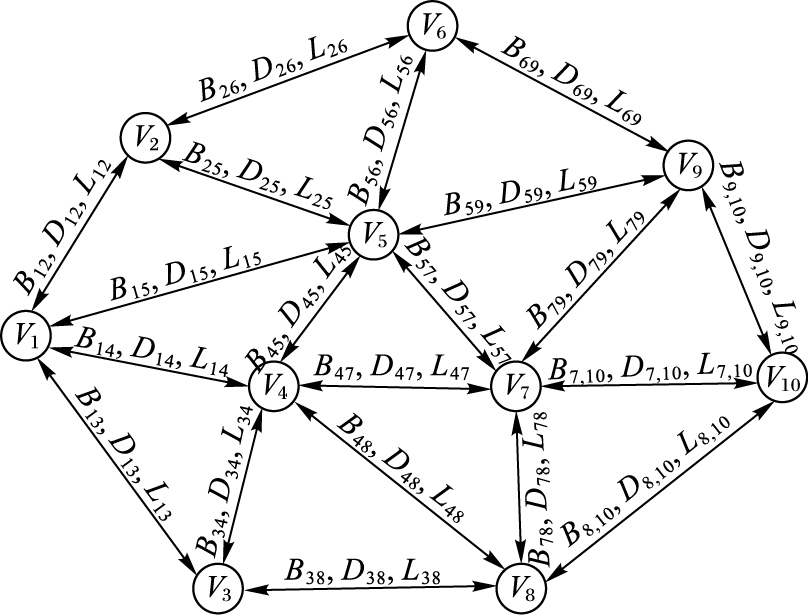
1 QoSR问题描述 1.1 QoSR网络模型约定图 1中的各符号函数如下:G=(V, E):表示该网络模型,其中V、E分表代表节点集和路径集;B、D、L分别表示典型的QoS度量参数:剩余可用带宽、传输时延及丢包率; Eij为节点Vi(i=1, 2, …,10) 到相邻节点Vj(j=1, 2, …, 10,且i≠j)的路径,Bij表示路径Eij的剩余可用带宽;Dij表示路径Eij的传输时延; Lij表示路径Eij的平均丢包率。
|
图 1 QoSR网络模型 Figure 1 QoSR network model |
QoSR问题就是求解源节点Vi(i=1, 2, …, 10) 到目标节点Vj(j=1, 2, …, 10,且i≠j)之间符合QoSR约束条件的最优路径。
以典型的QoS度量参数:剩余可用带宽、传输时延和丢包率为代表进行分析,满足QoSR约束条件的路由需符合以下条件:
1) QoSR请求路由中,每条路径的剩余可用带宽不应小于QoSR请求的最小带宽限制:
| ${\rm{Min }}{B_p}(p) \ge B,p \in {E_p}$ | (1) |
其中:Bp表示路径的剩余可用带宽,Ep表示QoSR请求的路径集合,p为该集合中的一条路径,B表示QoSR请求的最小可用带宽限制。
2) QoSR路由源点到终点的时延不应大于QoSR请求的最大时延限制:
| $\sum\limits_{n \in {V_n}} {{D_n}(n)} + \sum\limits_{p \in {E_p}} {{D_p}(p)} \le D$ | (2) |
其中:Dn表示路由节点处理时延,Dp表示路径时延,D表示QoSR请求的最大时延限制,Vn表示QoSR请求的节点集合,n为该集合中的一个节点,Ep,p符号的含义同式(1) 。
3) QoSR路由源点到终点的丢包率不应大于QoSR请求的最大丢包率限制:
| $\sum\limits_{n \in {V_n}} {{L_n}(n)} + \sum\limits_{p \in {E_p}} {{L_p}(p)} \le L$ | (3) |
其中:Ln表示路由节点的平均丢包率,Lp表示路径的平均丢包率,L表示QoSR请求的最大丢包率限制,Vn,n ,Ep,p符号的含义同式(1) 、式(2) 。
综合上述QoSR约束条件式(1) ~(3) ,得出多约束QoSR模型如下:
| ${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \matrix{ {\rm{Min }}{B_p}(p) \ge B,p \in {E_p} \hfill \cr \sum\limits_{n \in {V_n}} {{D_n}(n)} + \sum\limits_{p \in {E_p}} {{D_p}(p)} \le D \hfill \cr \sum\limits_{n \in {V_n}} {{L_n}(n)} + \sum\limits_{p \in {E_p}} {{L_p}(p)} \le L \hfill \cr} \right.$ | (4) |
蚁群算法求解QoSR问题,其实就是将所有m只蚂蚁放到源节点Va,将食物放到目标节点Vb,由蚂蚁自动搜寻食物,寻找符合QoSR约束条件的最优路径,将该过程简述如下:
步骤1 初始化源节点Va和目标节点Vb,初始化迭代次数x为1,初始化各节点和路径参数和各路径残余信息素。
步骤2 将m只蚂蚁放到源点位置Va。
步骤3 蚂蚁i(i=1, 2, …, m)根据路径综合代价值和路径上的残余信息素值为参考依据,选择下一节点,对经过的路径上的信息素进行局部更新,并将经过的节点加入到禁忌表UNi中,防止蚂蚁访问重复节点。
步骤4 第i+1只蚂蚁重复执行步骤3,直到m只蚂蚁都到达目标节点Vb,此时完成蚂蚁的一轮迭代。
步骤5 假设在本轮迭代中,蚂蚁i(i=1, 2, …, m)搜寻的路径为最优路径,其代价值fab x, min≤fab min,其中fab min表示当前记录的从Va和Vb的最优路径代价值,则令fab min=fab x, min,并且全局更新蚂蚁i在本次迭代中经过的路径的信息素。
步骤6 如果迭代次数x没有超过迭代次数上限xmax,则转至步骤2进行新一轮迭代(x++);否则,终止算法,令fab*=fab min,输出最优路径其中,fab*表示最终求出的从Va和Vb的最优路径代价值。
2.2 ACO算法的关键定义及规则1) 定义在t时刻路径Eij的剩余可用带宽、传输时延和丢包率的综合代价公式为fij(t),则有如下公式:
| ${f_i}_j(t) = \sigma ({{{D_{ij}}(\tau ) \cdot {L_{ij}}(t)} \over {{B_{ij}}(t)}})$ | (5) |
其中:σ是路径综合代价系数,该数值为一个常数;Bij、Dij和Lij分别表示在t时刻,路径Eij的剩余可用带宽、传输时延和平均丢包率;路径的综合代价对残余信息素有着决定性的作用。
2) 下一跳节点集合。
用禁忌表UNk来记录蚂蚁k已经走过的节点,用Ak表示允许蚂蚁k(k=1, 2, …, m)选择的下一跳节点集合,Qk表示蚂蚁k所在节点位置上所有相邻的节点集合,则有如下公式:
| ${A_K} = \{ Q{}_K - {Q_K} \cap U{N_K}\} $ | (6) |
3) 启发函数。
| ${\eta _{ij}}(t) = {1 \over {{f_{ij}}(t)}}$ | (7) |
对于蚂蚁而言,在t时刻路径Eij的综合代价fij(t)越小,则启发函数ηij(t)越大,ηij(t)用来表示蚂蚁从节点Vi到Vj的期望程度。
4) 下一跳节点选择概率公式。
定义τij(t)表示t时刻路径Eij上残余的信息量,蚂蚁根据相邻路径上的残余信息素选择下一跳,而信息素又是由路径综合代价决定的。所以,随着迭代次数的增加,综合代价小的路径上信息素将变得越来越浓。第k只蚂蚁在节点Vi位置上,选择下一跳节点为Vj的概率Pijk(t)为:
| ${P_{ij}}^k(t) = \left\{ \matrix{ {{|{\tau _{ij}}(t){|^\alpha } \cdot |{\eta _{ij}}(t){|^\beta }} \over {\sum\limits_{s \in {A_k}} {|{\tau _{is}}(t){|^\alpha } \cdot |{\eta _{is}}(t){|^\beta }} }} & j \in {A_k} \hfill \cr 0 & {\rm{其他}} \hfill \cr} \right.$ | (8) |
蚂蚁k在运动过程中根据各条路径上的信息素量决定转移的方向。由上式可知,由于
5) 信息素的局部更新公式。
在t时刻,蚂蚁k从节点Vi移动到相邻节点Vj(Vj∈AK)后,路径Eij上信息素浓度的局部更新公式为:
| ${\tau _{ij}}(t + 1) = (1 - \rho ) \cdot {\tau _{ij}}(t) + \rho \cdot \Delta \tau _{ij}^k$ | (9) |
| $\Delta \tau _{ij}^k = \theta {\eta _{ij}}(t)$ | (10) |
其中ρ∈(0, 1) ,表明在t时刻,蚂蚁k在从节点Vi到达Vj后,路径Eij上挥发的信息素浓度,Δτijk表示路径Eij上信息素浓度的增量,θ是一个常数,ηij(t)用来表示蚂蚁从节点Vi到Vj的期望程度。
6) 信息素全局更新公式。
假设在x次迭代后,第k只蚂蚁生成了当前最优解,则该蚂蚁经过的路径Eij上信息素浓度的全局更新公式如下:
| ${\tau _{ij}}^{new} = (1 - \rho ) \cdot {\tau _{ij}}^{old} + \rho \cdot \Delta {\tau _{ij}}^{}$ | (11) |
| $\Delta {\tau _{ij}} = \sum\limits_{k \in {s_x}}^{} {\Delta {\tau _{ij}}^k} $ | (12) |
其中:τijnew表示更新后路径Eij上的信息素浓度,τijold表示更新前路径Eij上的信息素浓度。Δτij为第x次迭代中,路径Eij上信息素的增量,初始时刻,Δτij(0) =0。Sx表示第x次迭代中生成最优解的蚂蚁集合,Δτijk表示第k只蚂蚁在本次迭代中由节点Vi到达Vj后,路径Eij上信息素的增量。
3 引入梯度下降的蚁群算法ACAGD 3.1 梯度下降法梯度下降法是一个有效的最优化算法,很多优化算法以它为基础进行改进和修正。梯度下降法最早由数学家Cauchy在1847年提出,该算法以某一点的负梯度方向作为下降方向[13],其简要步骤如下:
步骤1 求解函数f(a)的最优值,令初始点a0∈Rn,精度ε>0,x=0,x表示迭代次数;
步骤2 沿负梯度方向搜索,计算sx=-∇f(ax),如果‖sx‖≤ε,则停止迭代,最优值a*=ax;
步骤3 线性搜索:
梯度下降法在最优化中具有重要的理论意义,该算法中的下降方向反映了被优化目标的局部性质。本文将梯度下降法引入到蚁群的局部搜索过程中,结合残余信息素浓度,综合影响蚁群的下一跳选择行为,增强蚁群算法的局部搜索能力,在一定程度上,改进传统蚁群算法的搜索性能,尽量避免陷入局部最优的可能性。
3.2 ACAGD中蚂蚁局部搜索方法的改进传统蚁群算法中,蚂蚁完全依赖式(8) 搜索下一跳,也就是完全取决于当前节点和下一节点路径上的残余的信息量这一因素,该局部搜索机制很大程度上降低了蚁群算法的搜索效率,且容易陷入局部最优。为解决以上问题,特将梯度下降法引入到蚁群的局部搜索中,使得蚁群的搜索更具有全局性,在一定程度上提高寻找其他还未发现的优化路径的可能性,但简单的引入梯度下降法并不能避免局部最优问题。为解决该问题,特设计如下的局部搜索方法:
改进1 第i(i=1, 2, …, m)只蚂蚁在节点Vk(k=1, 2, …, n)位置上,选择下一跳节点的机制如下,其中pi∈(0, 1) :
1) 以概率pi按式(8) 进行搜索,确定蚂蚁下一跳;
2) 以概率1-pi按梯度下降法搜索,确定蚂蚁下一跳。
蚂蚁i的下一跳节点选择公式如式(13) 所示:
| $next\_hop=\left\{ \begin{array}{*{35}{l}} a(\text{8}) & {{p}_{i}} \\ \text{gradient}\ \text{descent}\ \text{algorithm,} & 1-{{p}_{i}} \\ \end{array} \right.$ | (13) |
改进2设置蚂蚁已搜寻路径中节点个数上限,屏蔽明显不合理的蚂蚁搜索路径。以hop*表示允许蚂蚁从源点Va到终点Vb搜寻过程中,所经过路径中包含的节点个数上限,如果超过hop*该蚂蚁还没有找到终点,则表示该蚂蚁搜索过的路径一定非最优路径,停止该蚂蚁搜索,在一定程度上提高蚂蚁搜索的准确率。
ACAGD的局部搜索使得蚂蚁i在搜索下一跳时,并不全部依赖于下一跳选择式(8) ,还有1-pi的概率基于梯度下降法进行搜索,信息素和梯度下降法的结合,使得蚁群算法降低了陷入局部最优的可能性;同时蚂蚁已搜寻路径中节点个数上限hop*的引入与干涉,使得蚂蚁搜索结果的准确率进一步得到提升。
3.3 ACAGD伪代码ACAGD伪代码如下,其中各项符号的解释参见本文第1章QoSR问题描述部分。
算法1 ACAGD。
1) Begin
2) Input G, Va, Vb, m, σ, a, b, c, n, hop*, x, xmax, ρ, p, α, β, UNi, ε等各项参数
3) For(i=1;i<=m;i++)
4) Va → ant i //蚂蚁i从源点Va开始搜索;
5) formula(13) → next hop of ant i
//蚂蚁i按照式(13) 搜寻下一跳;
6) next hop∈UNi //将下一跳节点加入到UNi;
7) Update{local pheromone} by formula (9) and (10) //按照式(9) 和(10)
更新局部信息素;
8) If(ant i !→ Vb) //如果蚂蚁i还没有到达终点Vb;
9) If(num of UNi <hop*)//
UNi中节点数小于hop*;
10) go to 5) ;
11) Else // UNi中节点数达到hop*;
12) stop(ant i) //蚂蚁i提前终止搜索;
13) Else //如果蚂蚁i已经到达终点Vb;
14) If(i <m) //还有其他蚂蚁未完成本次迭代;
15) {i++; go to 5) ;} //第m+1只蚂蚁搜索
16) Else// m只蚂蚁均已完成本次迭代
17) If(fab x, min≤fab min) //存在更优解
18) {Update{global pheromone}by (10) and (11) ,
fab min=fab x, min)}
//按照式(11) 和(12) 更新全局信息素,并且更新当前最优解
19) If(x≥xmax) //达到迭代次数上限
20) {fab*=fab min, //最优路径代价值
Output optimum solution} //输出最优解;
21) Else //还未达到迭代次数上限
22) {i=1, x++; go to 4) } //开始新一轮迭代
23) End
4 ACAGD的理论分析多约束QoSR问题本身是一个NP完全问题,因此改进蚁群算法求解多约束QoSR具有NP-C的复杂度。因为蚁群算法在t时刻达到最优状态的概率p*(t)在实际算法运行中很难准确确定[14],所以对于改进蚁群算法求解QoSR问题的收敛速度的时间界定很难进行理论求证;同时,ACAGD主要是改进蚂蚁的下一跳搜索策略,在一定程度上提高了寻找其他还未发现的优化路径的可能性,尽可能地避免了局部最优问题,重点不是改进蚁群算法的收敛速度,因此,本文主要从收敛性和复杂度两方面对改进蚁群算法ACAGD进行理论分析。
4.1 ACAGD的收敛性证明引理1 假设在ACAGD的全部迭代过程中,信息素浓度τij(t)的全局最大值为τmax,可行最优解集合为S(S∉),s*为S中一个解,τij(s*)为任意时刻路径Eij上最大的信息素浓度,μ为一常数,μ∈[0,1],对于∀tij,有如下公式成立:
| $\mathop {{\rm{lim}}}\limits_{t \to \infty } {\tau _{ij}}(t) \le {\tau _{\max }} = {{{\tau _{ij}}({s^*})} \over \mu }$ | (14) |
引理2 假设在ACAGD的全部迭代过程中,信息素浓度τij(t)的全局最小值为τmin。假设在t时刻,ACAGD求得的最优路径中包含Eij,该路径的信息素浓度为τij*(t),则应有τij*(t)≥tmin。参考ACAGD下一跳节点选择式(13) ,在每次迭代中,第i只蚂蚁在节点Vi,有pi的概率选择节点Vj,而pi∈[0.80, 0.85],因此τij*(t)有呈单调增加的趋势。对于∀(Vi, Vj)∈s*,应有如下公式成立:
| $\mathop {{\rm{lim}}}\limits_{t \to \infty } \tau _{ij}^*(t) = {\tau _{\max }} = {{\tau _{ij}^{}({s^*})} \over \mu }$ | (15) |
收敛性证明即证明定理1和定理2的过程。
定理1 假设p*(t)为t时刻内ACAGD求出最优解的概率,则对于∀δ>0和足够长的时间t,则有p*(t)≥1-δ,当t→∞时,应有式(16) 成立:
| $\mathop {\lim }\limits_{t \to \infty } {p^*}(t) = 1$ | (16) |
证明假设${\widehat p_{\min }}$为ACAGD经过xmax次迭代后,最差求解状况下的概率下界,结合引理1和引理2可以得出式(17) :
| ${\widehat p_{\min }} = {{\tau _{\min }^\alpha } \over {({x^{\max }} - 1)\tau _{\max }^\alpha + \tau _{\min }^\alpha }}$ | (17) |
其中:τmin为信息素浓度τij(t)的全局最大值,τmin为信息素浓度τij(t)的全局最小值,α为蚂蚁在运动中信息素对选择下一跳的影响权重参数,xmax为迭代次数上限。
假设pmin为ACAGD经过xmax次迭代后,最差求解状况下的概率,则有对于∀pmin,
| ${p^*}(t) = 1 - {(1 - \widehat p(t))^t}$ | (18) |
因
即
定理2 假设t0为ACAGD首次求得最优解的时刻,对于∀(vi, vj)∈s*,∀(x, y)∈ZG∩((x, y)∉s*),存在一个时刻Δt,当∀t>t0+Δt,应有式(19) 成立:
| ${\tau _{ij}}(t) > {\tau _{xy}}(t)$ | (19) |
其中:ZG是网络模型图G中两两相邻节点的集合。
证明 假设(vi, vj)∈s*,且τij*(t0)=τmin;假设(vx, vy)∈s*,且τxy*(t0)=τmax,在t0+t′时刻,则有式(20) 成立:
| $\begin{align} & \tau _{ij}^{*}({{t}^{0}}+{{t}^{'}})={{(1-\mu )}^{{{t}^{'}}}}\cdot {{\tau }_{\min }}+\sum\limits_{j=0}^{{{t}^{'}}-1}{{{(1-\mu )}^{j}}\cdot {{\tau }_{ij}}({{s}^{*}})} \\ & >{{t}^{'}}\cdot {{(1-\mu )}^{({{t}^{'}}-1)}}\cdot \tau _{ij}^{{}}({{s}^{*}}) \\ \end{align}$ | (20) |
在t0+t′时刻,有式(21) 成立:
| $\tau _{xy}^{*}({{t}^{0}}+{{t}^{'}})=\max \left\{ {{\tau }_{\min }},{{(1-\mu )}^{{{t}^{'}}}}\cdot {{\tau }_{\max }} \right\}$ | (21) |
可以推导出式(22) :
| $\tau _{ij}^{*}({{t}^{0}}+{{t}^{'}})>\tau _{xy}^{*}({{t}^{0}}+{{t}^{'}})$ | (22) |
当t′·(1-μ)(t′-1) ·τij*(s*)>(1-μ)t′·τmax时,即:
| ${{t}^{'}}>\frac{{{\tau }_{\max }}\cdot (1-\mu )}{{{\tau }_{ij}}({{s}^{*}})}$ |
结合引理2可以推导出式(23) :
| ${{t}^{'}}>(1-\mu )/\mu $ | (23) |
分析式(23) ,即t′∈(0, ∞)时式(22) 一直成立,因此可以推导出,当∀t>t0+Δt时,有定理2中的式(19) 成立:
即τij(t)>τxy(t) 证毕。
4.2 ACAGD复杂度分析 4.2.1 时间复杂度分析分析算法1可以得出,时间复杂度最高的语句应为5) ,即蚂蚁i选择下一跳语句的复杂度。而蚂蚁i选择下一跳又以概率pi按式(8) 确定下一跳;以概率1-pi按梯度下降法确定下一跳。无论是式(8) 还是梯度下降法,蚂蚁i选择下一跳时均与两个集合UNi及Ai相关,而UNi和Ai均与网络拓扑节点个数n直接相关,因此,算法1中语句5) 的时间复杂度应为O(n2)。
因蚂蚁数量为m,所以m个蚂蚁执行完一次全局搜索,时间复杂度为O(m·n2)。假设ACAGD收敛完毕需总共执行xmax次,则ACAGD的完整时间复杂度应为O(xmax·m·n 2),并没有增加原ACO算法的时间复杂度。
4.2.2 空间复杂度分析因网络拓扑节点数量为n,则网络拓扑模型G需要一个n×n的二维数组来存储数据,此处空间复杂度为O(n2);G中的信息素变量也需要一个n×n的二维数组来存储数据,此处空间复杂度也为O(n2);两个集合UNi及Ai中的元素均为G中的节点,因此空间复杂度为O(n),考虑到蚂蚁数量为m,此处空间复杂度为O(n·m)。
因此,ACO的空间复杂度应为O(n2)+O(n·m),但考虑到ACAGD为蚂蚁i搜索下一跳时引入了梯度下降法,需要增加额外的空间复杂度,其中,每只蚂蚁均需要一个梯度变量si 存储下一跳代价递减值,因为空间复杂度为O(m);而控制精度ε和搜寻路径中节点个数上限hop*均为常数,因此需要2个变量存储;综合以上分析ACAGD的复杂度为O(n2)+O((n+1) ·m)+2,基本等同于原ACO的空间复杂度O(n2)+O(n·m)。
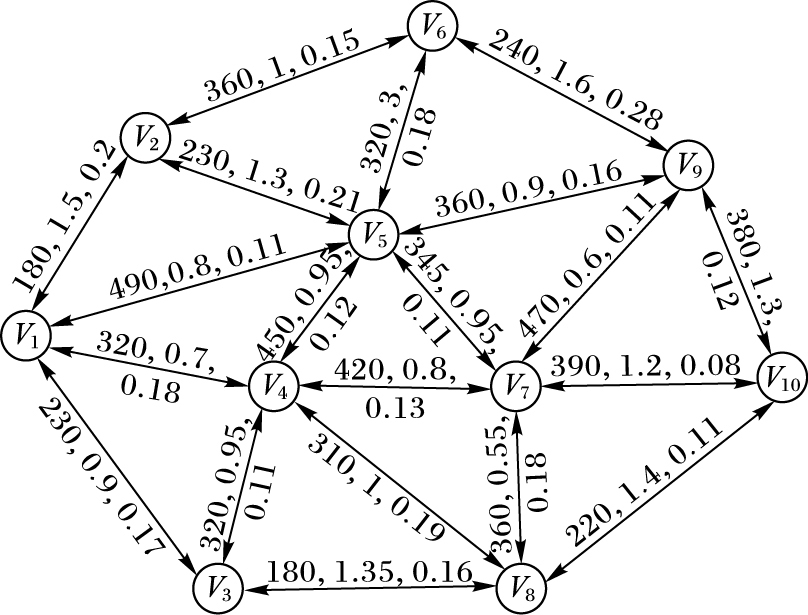
5 仿真实验与结果分析 5.1 仿真环境服务器采用HP ProLiant ML10,内存8GB,3100MHz主频四核CPU,Windows 7操作系统。采用Lingo 14.0软件进行算法建模,基于Waxman网络模型连续生成10~100个路由节点的仿真网络拓扑,构造邻接矩阵,随机给出基于剩余带宽、传输时延和丢包率的路径状态和约束条件。限于篇幅原因,节点过多时,网络拓扑图较难全部绘出。鉴于不同节点数量的网络模型图类似,只是节点数量不同。下面以其中10个路由节点的网络拓扑图作代表,见图 2(以10节点作代表,节点数量1~100) 。
|
图 2 实验拓扑图 Figure 2 Experimental topology |
图 2中,每条路径上的三个数字参数分别表示:剩余带宽(单位为Mb/s)、传输时延(单位为ms)和丢包率(单位为1%)。
5.2 ACAGD参数的实验分析 5.2.1 ACAGD参数的取值分析ACAGD的主要改进是在蚂蚁下一跳搜索策略,为保证ACO的收敛性,蚂蚁应以较大的概率按照下一跳搜索式(8) 来搜寻路由,以较小的概率按照梯度下降法来搜寻下一跳,因此,与梯度下降法没有直接关联的参数,可以参照一般改进蚁群算法求解QoSR问题的取值范围。参阅文献[10-11]可知,改进蚁群求解QoSR问题的主要参数一般设置如表 1所示。
| 表 1 求解QoSR问题的一般参数 Table 1 General parameters for solving QoSR problem |
而参数pi和ε是梯度下降法中的重要参数,它们的取值对于ACAGD的收敛性能和稳定性有着重要的影响。其中,pi则控制着蚂蚁i以1-pi的概率按照梯度下降法来搜索下一跳,而ε控制着蚂蚁i对比下一跳路径代价差的对比精度。下面将对这两个参数的取值范围,进行详细的实验证明。
5.2.2 不同参数组合的实验分析1) 实验方法与计算公式。
本实验主要进行ACAGD参数的稳定性实验分析。仿真实验采用Lingo 14.0软件进行仿真。为增加算法的计算复杂度,在不同路由节点的网络拓扑中,随机选取相距较远的两节点作为源点和终点,在参数pi和ε的不同组合下,应用ACAGD进行100次独立实验,每次实验结果的路由代价值s和收敛时间t,并计算其中最优实验结果的路由代价s*,最小的收敛时间t*,以及100次实验的路由代价平均值s和收敛时间的平均值。假设第i次实验结果的路由代价值为si,收敛时间为ti则有如下公式:
| ${s^*} = \min \{ {s_1},{s_2},...{s_{100}}\} $ | (24) |
| $\bar s = \sum\limits_{i = 1}^{100} {{s_i}} /100$ | (25) |
| $t* = \min \{ {t_1},{t_2},...{t_{100}}\} $ | (26) |
| $\bar{t}=\sum\limits_{i=1}^{100}{{{t}_{i}}}/100$ | (27) |
根据统计学理论,定义如下样本偏差公式:
| $\vartriangle s=\sqrt{\frac{1}{100}\cdot \sum\limits_{i=1}^{100}{{{({{s}_{i}}-\bar{s})}^{2}}}}$ | (28) |
即:
| $\vartriangle s=\frac{1}{10}\sqrt{\cdot \sum\limits_{i=1}^{100}{{{({{s}_{i}}-\bar{s})}^{2}}}}$ | (29) |
| $\vartriangle t=\sqrt{\frac{1}{100}\cdot \sum\limits_{i=1}^{100}{{{({{t}_{i}}-\bar{t})}^{2}}}}$ | (30) |
即:
| $\vartriangle t=\frac{1}{10}\sqrt{\cdot \sum\limits_{i=1}^{100}{{{({{t}_{i}}-\bar{t})}^{2}}}}$ | (31) |
其中:Δs为100次实验所求的路由代价的偏差,Δt为收敛时间的偏差,偏差Δs和Δt越小,表明ACAGD的稳定性越高。
2) 参数的取值范围。
根据网络拓扑中剩余带宽、传输时延及丢包率的一般取值范围进行经验总结,ε∈[0.05, 0.15]是比较合适的取值范围,如果ε取值超过此集合上限,容易触发梯度下降法,降低ACAGD的收敛速度;而如果ε取值低于此集合下限,则难以让梯度下降法搜索到有意义的下一跳,失去了ACAGD改进的意义。
蚂蚁i下一跳搜索概率pi的取值对ACAGD的搜索结果有较大的影响,如果pi的取值趋近于1,则使得ACAGD失去了梯度下降法搜索的作用;pi的取值如果过小,则使得ACAGD的局部搜索很大程度上偏离了原始ACO局部搜索式(8) 的搜索结果,容易出现寻优结果的不稳定性,难以快速收敛。ACAGD收敛结果的稳定性主要还是体现在ACO算法的稳定性上,根据大量仿真实验数据分析,pi∈[0.80, 0.95]是合理的取值空间。
以上是ACAGD的参数pi和ε的较为粗糙的取值空间,为获取更具指导意义的参数取值范围,将参数pi和ε的实验取值范围进行组合编排进行实验验证,具体参数组合和取值范围列在表 2。
| 表 2 参数组合和取值范围 Table 2 Parameter combination and range |
3) 实验结果分析。
在表 2描述出的不同参数组合条件下,应用ACAGD算法分别进行100次独立实验,分别记录每次实验的路由低价和收敛时间,按照式(25) 和式(27) 计算路由代价的平均值、收敛时间的平均值,按照式(29) 和式(31) 计算路由代价的偏差以及收敛时间的偏差,将结果绘于图 3~6中。
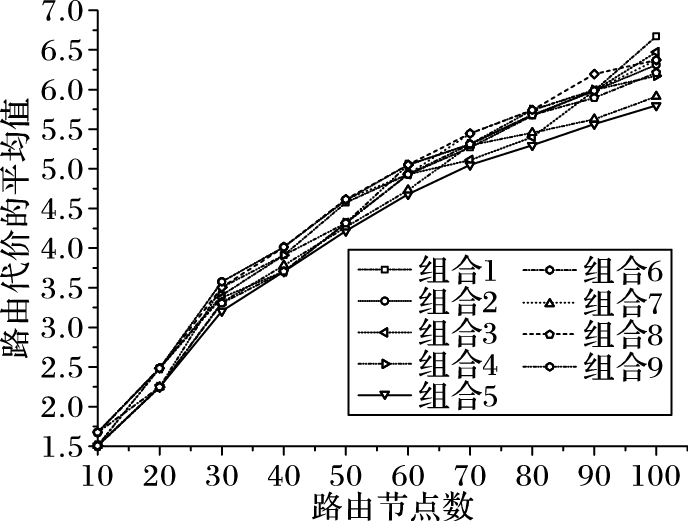
|
图 3 不同参数组合下的路由代价平均值 Figure 3 Average routing cost under different parameter combinations |
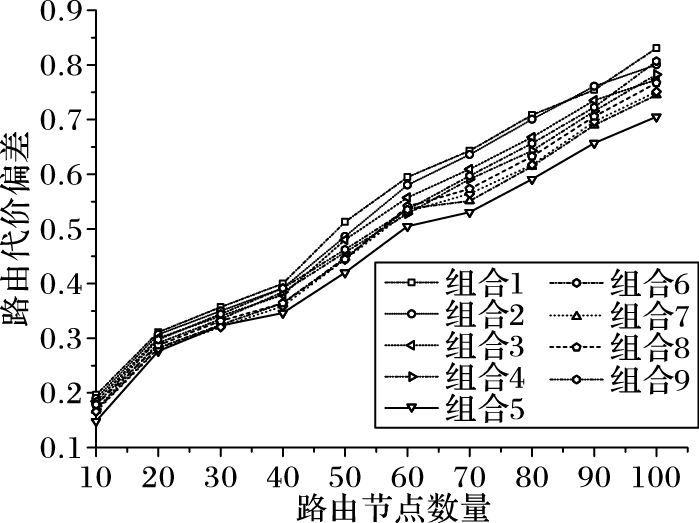
|
图 4 不同参数组合下的路由代价偏差 Figure 4 Routing cost deviation under different parameter combinations |
|
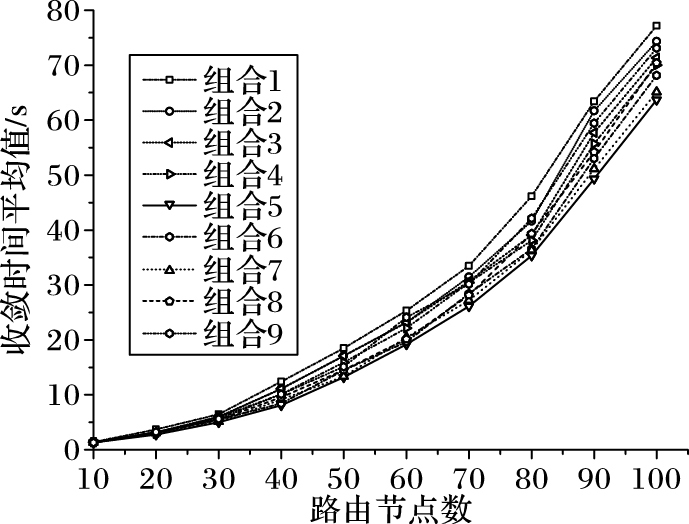
图 5 不同参数组合下的收敛时间平均值 Figure 5 Convergence time average under different parameter combinations |
|
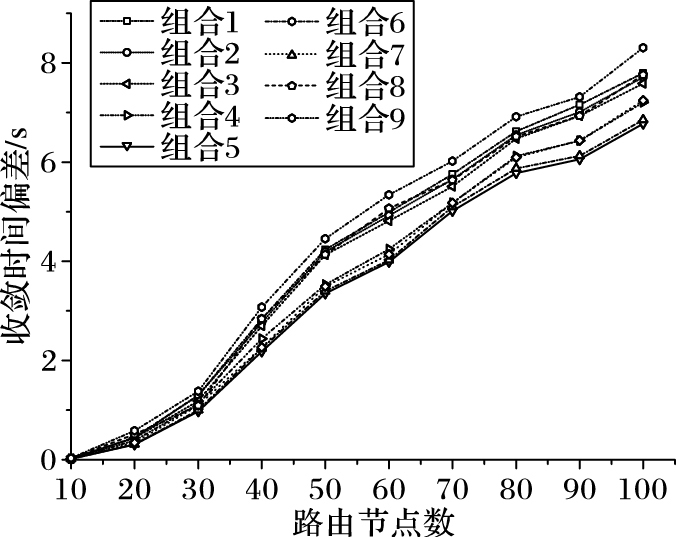
图 6 不同参数组合下的收敛时间偏差 Figure 6 Convergence time deviation under different parameter combinations |
分析图 3,参数组合5或者组合6的路由代价平均值一直处于相对较低的位置,表明在这两组参数条件下,ACAGD的收敛结果较好。
分析图 4,参数组合5的路由代价偏差一直较低,表明在参数组合5的条件下,ACAGD收敛结果的稳定性较好。
分析图 5,参数组合5和组合7的收敛时间相对较小,表明在这两组参数条件下,ACAGD的收敛速度较好。
分析图 6,参数组合5和组合6的收敛时间偏差相对较低,表明在参数组合5和组合6的条件下,ACAGD收敛速度的稳定性较好。
将以上实验结果简列于表 3。
| 表 3 较优的参数组合 Table 3 Better parameter combinations |
分析表 3,可以看出,在参数组合5的条件下,ACAGD的收敛结果和收敛速度都较为优秀,且收敛结果和收敛速度的稳定性也相对较好。
因此,在参数组合5以及表 1中的参数条件下,将ACAGD同其他改进蚁群算法进行对比实验。
5.3 ACAGD同其他算法的对比实验仿真实验采用Lingo 14.0软件进行仿真,为增加算法的计算复杂度,在不同路由节点的网络拓扑中,随机选取相距较远的两节点作为源点和终点,针对每次路由请求分别用ACAGD、叶华乔蚁群算法、量子蚁群算法、基于云模型的多目标蚁群算法CMACA和基于蚁群的分布式多约束QoSR算法分别进行100次独立实验。
5.3.1 算法收敛结果和收敛速度的对比分析对以上五种改进蚁群算法分别进行100次独立实验,分别记录每次实验的路由代价和收敛时间,按照式(25) 和式(27) 计算以上五种算法收敛后的路由代价和收敛时间的平均值,如图 7、8所示。
|
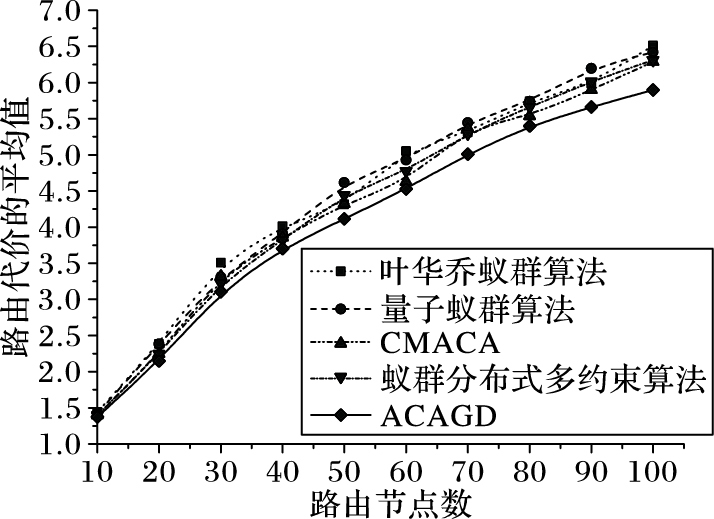
图 7 不同算法的路由代价平均值 Figure 7 Average value of routing cost for different algorithms |
|
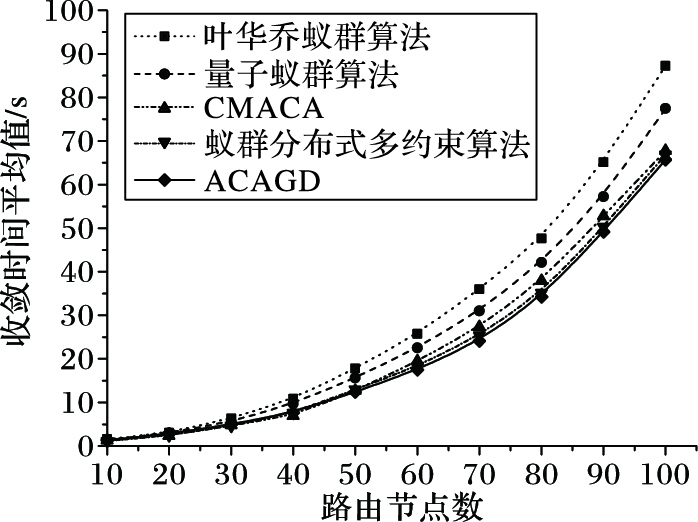
图 8 不同算法的收敛时间平均值 Figure 8 Mean value of convergence time for different algorithms |
分析图 7,五种改进蚁群算法在含有较少路由节点的网络环境中,搜寻到的路径总路由代价的平均值基本相同,但随着网络路由节点的增加,ACAGD、CMACA和蚁群分布式多约束算法的总路由代价的平均值相比其他两种算法一直有一定的优势,尤其是ACAGD的路由代价的平均值一直处于相对较低的位置,且优势越来越明显,表明ACAGD在避免陷入局部最优的改进上取得了一定成功。这是由于ACAGD中蚂蚁进行下一跳搜索时不仅仅依赖于信息素浓度,还取决于梯度下降法,因此ACAGD在一定程度上提高了寻找其他还未发现的优化路径的可能性,尽可能地避免了局部最优问题,搜寻到了综合代价相对较低的路由。
分析图 8,五种改进蚁群算法在含有较少路由节点的网络环境中,达到收敛所需的收敛时间的平均值基本相同,且随着网络路由节点的增加均呈上升趋势,但ACAGD、CMACA和蚁群分布式多约束算法的收敛时间的平均值相比其他两种算法较少的优势却越发明显。表明在中大型网络拓扑中,ACAGD、CMACA和蚁群分布式多约束算法的搜索QoSR路由速度有一定程度的优势,但ACAGD的收敛时间相比CMACA和蚁群分布式多约束算法并没有明显的优势,这是因为在蚁群的局部搜索中引入梯度下降法是为了避免陷入传统蚁群的局部最优问题,并不是追求收敛速度,但ACAGD并没有明显提高传统蚁群算法的复杂度,因此,ACAGD的收敛速度仍不差。
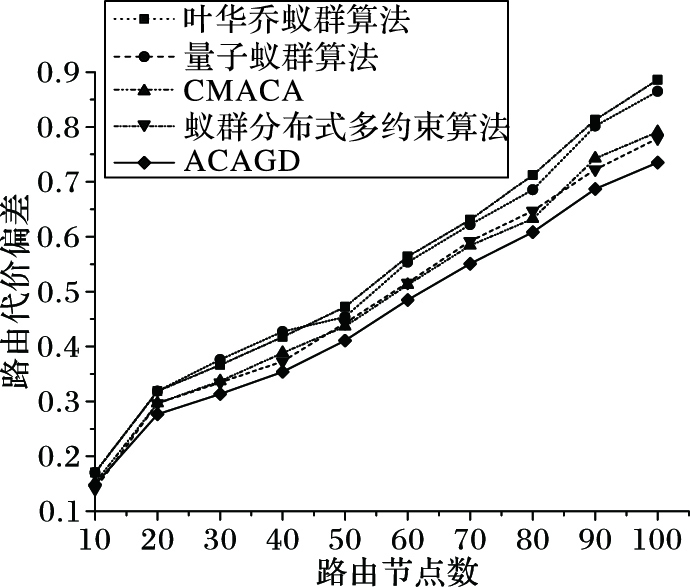
5.3.2 算法稳定性的对比分析算法稳定性的对比,主要从收敛结果和收敛时间的稳定性两方面去验证,因此,将以上五种改进蚁群算法分别进行100次独立实验,分别记录每次实验的路由代价和收敛时间,按照式(29) 和式(31) 计算以上五种算法收敛后的路由代价的偏差以及收敛时间的偏差,结果如图 9~10所示。
|
图 9 不同算法的路由代价偏差 Figure 9 Routing cost deviation for different algorithms |
分析图 9和图 10,可以看出ACAGD的路由代价偏差和收敛时间偏差相比于其他改进蚁群算法更小,且随着路由节点数量的增加,ACAGD偏差值的优势更加明显。实验结果证明了ACAGD具有相对较好的稳定性,比较适合用于求解多约束QoSR问题,特别是在中大型网络拓扑下,ACAGD的稳定性更加明显。
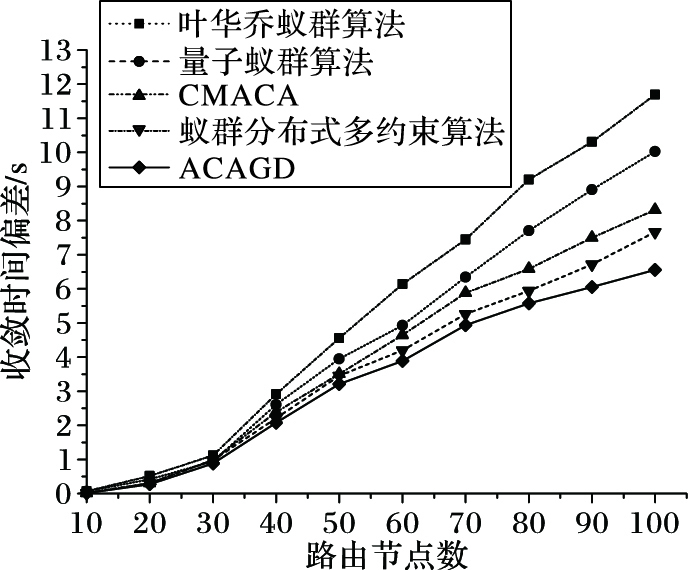
|
图 10 不同算法的收敛时间偏差 Figure 10 Convergence time deviation for different algorithms |
利用改进蚁群算法求解多约束服务质量路由一直是路由优化领域内的研究热点,本文将梯度下降法引入到到蚁群的局部搜索中,提出一种引入梯度下降的蚁群算法ACAGD。仿真实验结果表明,同其他改进蚁群算法相比,ACAGD在收敛速度不受影响的情况下搜寻到了综合路径代价相对较低的路由,且该算法的稳定性较好,为解决实际网络中的QoSR问题,提供了一条新的思路。下一步将对ACAGD的收敛速度作进一步研究。
| [1] | 夏小云.随机启发式搜索算法的性能分析[D].广州:华南理工大学,2015:11. ( XIA X Y. On the performance analysis of randomized search heuristics[D]. Guangzhou:South China University of Technology, 2015:11. ) |
| [2] | STVTZLE T, HOOS H H. MAX-MIN ant system[J]. Future Generation Computer Systems, 2000, 16 (9) : 889-914. |
| [3] | 杨洁, 杨胜, 曾庆光, 等. 基于信息素强度的蚁群算法[J]. 计算机应用, 2009, 29 (3) : 865-867. ( YANG J, YANG S, ZENG Q G, et al. Ant colony algorithm based on pheromone intensity[J]. Journal of Computer Applications, 2009, 29 (3) : 865-867. doi: 10.3724/SP.J.1087.2009.00865 ) |
| [4] | 段海滨, 马冠军, 王道波, 等. 一种求解连续空间优化问题的改进蚁群算法[J]. 系统仿真学报, 2007, 19 (5) : 974-977. ( DUAN H B, MA G J, WANG D B, et al. Improved ant colony algorithm for solving continuous space optimization problems[J]. Journal of System Simulation, 2007, 19 (5) : 974-977. ) |
| [5] | 叶华乔. 基于改进蚁群算法的计算机网络路由优化研究[J]. 计算机仿真, 2015, 32 (4) : 265-268. ( YE H Q. Research on routing optimization of computer network based on improved ant colony algorithm[J]. Computer Simulation, 2015, 32 (4) : 265-268. ) |
| [6] | 王宏霞, 李亚龙. 求解QoS最佳路由选择问题的量子蚁群算法[J]. 计算机仿真, 2014, 31 (3) : 295-298. ( WANG H X, LI Y L. Quantum ant colony algorithm for QoS best routing problem[J]. Computer Simulation, 2014, 31 (3) : 295-298. ) |
| [7] | 刘朝华, 张英杰, 章兢, 等. 蚁群算法与免疫算法的融合及其在TSP中的应用[J]. 控制与决策, 2010, 25 (5) : 695-700. ( LIU Z H, ZHANG Y J, ZHANG J, et al. Using combination of ant algorithm and immune algorithm to solve TSP[J]. Control and Decision, 2010, 25 (5) : 695-700. ) |
| [8] | 刘朝华, 张英杰, 李小花, 等. 双态免疫优势蚁群算法及其在TSP中的应用研究[J]. 小型微型计算机系统, 2010, 31 (5) : 937-941. ( LIU Z H, ZHANG Y J, LI X H, et al. Research of using binary state ACA based on immunodominance to solve TSP[J]. Journal of Chinese Computer Systems, 2010, 31 (5) : 937-941. ) |
| [9] | 邢志娟.多目标优化问题的蚁群算法研究[D].北京:中国地质大学,2010:5. ( XING Z J. Study on multi-objective optimization problem based on ant colony optimization algorithm[D]. Beijing:China University of Geosciences, 2010:5. ) |
| [10] | 王永.多目标路由问题中的蚁群优化算法研究[D].长沙:湖南大学,2009:5. ( WANG Y. The research on multi-objective routing problems based on ant colony optimization algorithm[D]. Changsha:Hunan University, 2009:5. ) |
| [11] | 王健安.基于蚁群优化算法的分布式多约束QoS路由算法研究[D].长春:长春理工大学,2014:3. ( WANG J A. Research of multiple constrained distributed QoS routing based on improved ant colony algorithm[D]. Changchun:Changchun University of Science and Technology, 2014:3. ) |
| [12] | 宋悦.蚁群算法在路由优化中的应用研究[D].北京:北京交通大学,2015:4. ( SONG Y. The study and application of ant colony algorithm in the field of routing optimization[D]. Beijing:Beijing Jiaotong University, 2015:4. ) |
| [13] | 胡朝明.几类谱共轭梯度方法理论及数值行为研究[D].长沙:中南大学,2012:9. ( HU C M. Research on some types of spectral conjugate gradient methods from the viewpoints of theory and numerical performance[D]. Changsha:Central South University, 2012:9. ) |
| [14] | 黄翰, 郝志峰, 吴春国, 等. 蚁群算法的收敛速度分析[J]. 计算机学报, 2007, 30 (8) : 1345-1353. ( HUANG H, HAO Z F, WU C G, et al. The convergence speed of ant colony optimization[J]. Chinese Journal of Computers, 2007, 30 (8) : 1345-1353. ) |




