兰州大学 信息科学与工程学院, 兰州 730000
收稿日期:2016-09-19;修回日期:2016-11-11
基金项目:国家自然科学基金面上项目(61272213);中央高校基本科研业务费专项资金资助项目(lzujbky-2016-k07,lzujbky-2016-142)
作者简介:张变兰(1991-),女,山西吕梁人,硕士研究生,主要研究方向:模式识别;
张海涛(1986-),男,甘肃兰州人,博士,主要研究方向:模式识别、软件工程
通讯联系人:路永钢(1974-),男,甘肃陇南人,教授,博士,CCF会员,主要研究方向:模式识别、人工智能、生物信息. E-mail:
ylu@lzu.edu.cn
Spherical embedding algorithm based on Kullback-Leibler divergence and distances between nearest neighbor points
School of Information Science and Engineering, Lanzhou University, Lanzhou Gansu 730000, China
Foundation Item: This work is partially supported by the National Natural Science Foundation of China (61272213), the Fundamental Research Funds for the Central Universities (lzujbky-2016-k07, lzujbky-2016-142)
Author introduction: ZHANG Bianlan, born in 1991, M.S. candidate. Her research interests include pattern recognition;
ZHANG Haitao, born in 1986, Ph.D. Her research interests include pattern recognition, software engineering
Corresponding author:
LU Yonggang, born in 1974, Ph.D., professor. His research interests include pattern recognition, artificial intelligence, bioinformatics. E-mail:
ylu@lzu.edu.cn
0 引言
近年来,数据可视化分析已经成为处理大数据的重要方法之一。研究表明,人们从外界接收的各种信息中80%以上是通过视觉获得的[1]。通过对大数据可视化,人们可以对数据产生直观的理解,以便对其进行分析和研究,因此,数据可视化在大数据分析中正起着越来越重要的作用。为了避免维数灾难带来的影响,以及更好地对大数据进行可视化分析[2],数据降维方法常被用来产生数据的一个低维可视化表示。
在计算机视觉和模式识别中,许多问题都是基于样本点间的距离的,例如手势识别和形状识别等。在这些问题中,只知道样本点间的相似性或者距离度量,而不知道样本在原始空间的坐标或者其对应的特征向量。这时,可以使用嵌入算法来得到样本点在对应空间中的坐标分布。在嵌入低维的情况下,也可以通过降维得到样本的可视化表示。处理该类问题的嵌入算法有多维尺度分析(MultiDimensional Scaling,MDS)[3]、最 大 方 差 展 开 (Maximum Variance Unfolding,MVU)[4]、等距映射(Isometric Mapping,IsoMap)[5]和t分布随机邻域嵌入(t-Distributed Stochastic Neighbor Embedding,t-SNE)[6]等,它们都是利用所有样本间的相似性或者距离信息来构建样本的低维表示,并使得样本在低维空间中的结构与高维空间的分布尽量保持一致[3, 7]。
然而,这类算法大部分都是将数据嵌入线性空间。在计算机视觉中,对于很多类型的数据,其样本都是分布在高维非线性空间中的,因此,将这些数据嵌入至低维线性空间是不可行的[8-9]。针对上述问题,出现了很多基于曲面的嵌入算法,例如将数据嵌入环形表面或者球面,以便对此类数据进行可视化研究。其中,关于球面嵌入的研究更为广泛,而且球面嵌入算法有很多实际应用,例如在地球模型表面的数据表示,或类球状物表面的纹理贴图等[8, 10]。文献[10-11] 中的算法都能够有效地将数据嵌入至球面空间,它们都是基于MDS算法的改进,最终成功将数据嵌入到非线性空间[8]。这类算法的关键步骤是优化过程,它们首先定义一个衡量嵌入质量的目标函数[8, 10-11],然后通过优化算法不断调整低维空间中样本点的位置来优化目标函数。文献[11]中提出了一种球面MDS的嵌入算法,这是最早提出球面嵌入算法的论文之一。它用球面极坐标来表示样本点,用克鲁斯克系数(Kruskal Stress)[11]构造目标函数。算法采用了最速下降法进行优化,通过调整点在球面的位置来使目标函数最小。文献[8]中,提出了一种曲面流形嵌入算法,将已知的所有点对间距离的数据集嵌入恒定曲率的曲面空间,如球面或双曲面,并且可求出该曲面空间的曲率半径;该算法还可以将数据嵌入超球面空间。该算法的最大优点是,在无需任何优化的情况下,根据已知的对称距离矩阵可以快速有效地将数据嵌入曲面空间,并估计出曲面空间的曲率半径;但是,现有的球面嵌入算法的共同缺点是,必须利用所有点间的相似性或距离信息来进行嵌入。
而对于许多高维数据来说,只有近邻点间的相似性度量是比较可靠的,所以大多数非线性降维算法只采用近邻点间的距离进行低维嵌入,例如MVU[4]、IsoMap[5]和局部线性嵌入(Locally Linear Embedding,LLE)[12]等。这些算法的本质是,先找到每个样本点的前K个近邻点,通过优化目标函数,使得近邻点间的距离尽量保持不变,从而将非线性数据嵌入至线性空间。
本文提出了一种新的球面嵌入算法,能够在只知道近邻点间距离的情况下将数据集嵌入到单位球面上,并尽量保持近邻点间的结构。这样就实现了只利用近邻点间的相似性信息,将非线性数据嵌入至球面空间。据考证,目前还没有类似的算法,而本文是首次提出了基于近邻点间距离的球面半径未知情况下的球面嵌入算法。该方法用KL散度[13-14]来计算嵌入球面前后每对近邻点间的相对分布差异,并基于此差异构建出目标函数。然后利用带有动量的随机梯度下降法[15-16]进行优化,使得所有近邻点间相对分布的差异之和最小。这样就可以将任意尺度的高维数据嵌入到单位球面上。最后,利用嵌入前后所有近邻点间的距离之和的比值,就可估计出适合原始数据分布的球面半径。
1 球面嵌入算法
1.1 球面上的距离计算
在球面坐标系中,球面上的点的坐标为xi=(θi,φi),极角θi表示向量xi与z轴的夹角,方位角φi表示向量xi与x轴的夹角。在球面上,两点间的距离为两向量间夹角对应的球面上的弧长。若在半径为r的球面上,两点间的夹角记为Θij,则它们在此球面上的距离可表示为:
|
${d_{ij}} = r{\mathit{\Theta }_{ij}}$
|
(1) |
|
$\begin{array}{l}
{\mathit{\Theta }_{ij}} = {\cos ^{ - 1}}\left( {\cos {\theta _i}\cos {\theta _j} + \sin {\theta _i}\sin {\theta _j}\cos \left( {{\varphi _i} - {\varphi _j}} \right)} \right)\\
\end{array}$
|
(2) |
1.2 球面嵌入算法
首先,该算法将输入的所有近邻间的距离整体归一化。对于样本点xi和点xj,其归一化距离为pij:
|
${p_{ij}} = {d_{ij}}/\left( {\sum\limits_{m \ne n} {{w_{mn}}{d_{mn}}} } \right)$
|
(3) |
|
${d_{ij}} = \left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|$
|
(4) |
嵌入单位球面空间后,用同样的归一化方法,可得到点yi与点yj的归一化距离qij:
|
${q_{ij}} = {\mathit{\Theta }_{ij}}/\left( {\sum\limits_{m \ne n} {{w_{mn}}{\mathit{\Theta }_{mn}}} } \right)$
|
(5) |
|
${\mathit{\Theta }_{ij}} = \left\| {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{y}}_j}} \right\|$
|
(6) |
其中:Θij表示嵌入到单位球面上的两点间的距离,也就是两点对应的向量间的夹角。另外,该算法中定义了一个系数因子w,当点xi和点xj为近邻时,wij=1,否则wij=0。算法将只利用wij=1的这部分归一化距离进行数据嵌入。
对于任意wij=1对应的两个近邻点,如果嵌入单位球面后的归一化距离qij和原始样本点间的归一化距离pij相等,就意味着嵌入前后这两点的相对分布一致,因此,该算法的目标就是在嵌入的球面空间中调整近邻点的位置分布,使得每对近邻点之间pij和qij的差异最小,进而使得所有近邻点间的归一化距离在嵌入前后的差异之和达到最小。本文利用KL散度作为衡量pij和qij间差异的指标,因此,所有近邻点之间的KL散度之和构成目标函数:
|
$C = \sum {KL\left( {P||Q} \right) = \sum\limits_i {\sum\limits_j {{w_{ij}}({p_{ij}}\ln {\textstyle{{{p_{ij}}} \over {{q_{ij}}}}})} } } $
|
(7) |
此目标函数的梯度为:
|
$\nabla C = (\frac{{\partial C}}{{\partial {\theta _i}}},\frac{{\partial C}}{{\partial {\varphi _i}}})$
|
(8) |
|
$\frac{{\partial C}}{{\partial {\theta _i}}} = \frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}}\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}}}$
|
(9) |
|
$\frac{{\partial C}}{{\partial {\varphi _i}}} = \frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}}\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\varphi _i}}}$
|
(10) |
|
$\frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}} = \frac{{{q_{ij}} - {p_{ij}}}}{{{\mathit{\Theta }_{ij}}}}$
|
(11) |
|
$\begin{array}{l}
\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}}} = \frac{{\sin {\theta _i}\cos {\theta _j} - \cos {\theta _i}\sin {\theta _j}\cos ({\varphi _i} - {\varphi _j})}}{{\sin {\mathit{\Theta }_{ij}}}}\\
\end{array}$
|
(12) |
|
$\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\varphi _i}}} = \frac{{\sin {\theta _i}\sin {\theta _j}\sin ({\varphi _i} - {\varphi _j})}}{{\sin {\mathit{\Theta }_{ij}}}}$
|
(13) |
在该球面嵌入算法中,首先将单位球面上随机产生的样本点分布作为嵌入空间中的初始分布,然后采用带有动量的随机梯度下降法进行优化,具体的迭代过程为:
|
$\mathit{\boldsymbol{y}}_i^{(k)} = \left( {\theta _i^{(k)},\varphi _i^{(k)}} \right)$
|
(14) |
|
$\mathit{\boldsymbol{y}}_i^{(k + 1)} = \mathit{\boldsymbol{y}}_i^{(k)} + \Delta \mathit{\boldsymbol{y}}_i^{(k + 1)}$
|
(15) |
|
$\Delta \mathit{\boldsymbol{y}}_i^{(k + 1)} = - {\rho ^{(k)}}\frac{{\nabla C(\mathit{\boldsymbol{y}}_i^{(k)})}}{{\left\| {\nabla C(\mathit{\boldsymbol{y}}_i^{(k)})} \right\|}} + \alpha \Delta \mathit{\boldsymbol{y}}_i^{(k)}$
|
(16) |
|
$\alpha = \left\{ {\begin{array}{*{20}{c}}
{0.5{\kern 1pt} ,k < 250}\\
{0.8,k \ge 250}
\end{array}} \right.$
|
(17) |
|
${\rho ^{(k)}} = \frac{{\sum\limits_{i = 1}^N {\left\| {\nabla C(\mathit{\boldsymbol{y}}_i^{(k)})} \right\|} }}{{\sum\limits_{i = 1}^N {\frac{{\nabla C{{(\mathit{\boldsymbol{y}}_i^{(k)})}^{\rm{T}}}{\bf{D}}(\mathit{\boldsymbol{y}}_i^{(k)})\nabla C(\mathit{\boldsymbol{y}}_i^{(k)})}}{{{{\left\| {\nabla C(\mathit{\boldsymbol{y}}_i^{(k)})} \right\|}^2}}}} }}$
|
(18) |
式(16) 中,α表示动量;k表示迭代次数;Δyi表示在每次迭代后样本点i的位置的变化量,带动量的随机梯度下降法每次都记录这个位置变化,并利用梯度和前一次的位置变化量的组合得出新的位置变化量;ρ(k)表示第k次迭代的最佳步长,确定最佳步长的计算过程见式(18) 。在式(18) 中,D(yi) 为C(yi)的二阶偏导数矩阵,详细计算过程为:。
|
$\mathit{\boldsymbol{D}} = \left( {\begin{array}{*{20}{c}}
{\frac{{{\partial ^2}C}}{{\partial \theta _i^2}}} & {\frac{{{\partial ^2}C}}{{\partial {\theta _i}\partial {\varphi _i}}}}\\
{\frac{{{\partial ^2}C}}{{\partial {\theta _i}\partial {\varphi _i}}}} & {\frac{{{\partial ^2}C}}{{\partial \varphi _i^2}}}
\end{array}} \right)$
|
(19) |
其中:
|
$\frac{{{\partial ^2}C}}{{\partial {\theta _i}^2}} = \frac{{{\partial ^2}C}}{{\partial \mathit{\Theta }_{ij}^2}}{\left( {\frac{{\partial C}}{{\partial {\theta _i}}}} \right)^2} + \frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}}\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial \theta _i^2}}$
|
(20) |
|
$\frac{{{\partial ^2}C}}{{\partial {\theta _i}\partial {\varphi _i}}} = \frac{{{\partial ^2}C}}{{\partial \mathit{\Theta }_{ij}^2}}\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}}}\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\varphi _i}}} + \frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}}\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}\partial {\varphi _i}}}$
|
(21) |
|
$\frac{{{\partial ^2}C}}{{\partial \varphi _i^2}} = \frac{{{\partial ^2}C}}{{\partial \mathit{\Theta }_{ij}^2}}{\left( {\frac{{\partial {\Theta _{ij}}}}{{\partial \varphi }}} \right)^2} + \frac{{\partial C}}{{\partial {\mathit{\Theta }_{ij}}}}\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial \varphi _i^2}}$
|
(22) |
|
$\frac{{{\partial ^2}C}}{{\partial \mathit{\Theta }_{ij}^2}} = \frac{{{p_{ij}} - q_{ij}^2}}{{\mathit{\Theta }_{\mathit{ij}}^\mathit{2}}}$
|
(23) |
|
$\begin{array}{l}
\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial \theta _i^2}} = \frac{{\cos {\theta _i}\cos {\theta _j} + \sin {\theta _i}\sin {\theta _j}\cos ({\varphi _i} - {\varphi _j})}}{{\sin {\mathit{\Theta }_{ij}}}} - {(\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}}})^2}\frac{{\cos {\mathit{\Theta }_{ij}}}}{{\sin {\mathit{\Theta }_{ij}}}}\\
\end{array}$
|
(24) |
|
$\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}\partial {\varphi _i}}} = \frac{{\cos {\theta _i}\sin {\theta _j}\sin ({\varphi _i} - {\varphi _j})}}{{\sin {\mathit{\Theta }_{ij}}}} - \frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\theta _i}}}\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\varphi _i}}}\frac{{\cos {\mathit{\Theta }_{ij}}}}{{\sin {\mathit{\Theta }_{ij}}}}$
|
(25) |
|
$\frac{{{\partial ^2}{\mathit{\Theta }_{ij}}}}{{\partial \varphi _i^2}} = \frac{{\sin {\theta _i}\sin {\theta _j}\cos ({\varphi _i} - {\varphi _j})}}{{\sin {\mathit{\Theta }_{ij}}}} - {\left( {\frac{{\partial {\mathit{\Theta }_{ij}}}}{{\partial {\varphi _i}}}} \right)^2}\frac{{\cos {\mathit{\Theta }_{ij}}}}{{\sin {\mathit{\Theta }_{ij}}}}$
|
(26) |
最后,在求得嵌入单位球面的样本之后,即可利用嵌入前后近邻点间的距离之和的比值,求出原始样本分布的球面半径R,公式如下:
|
$R = \left( {\sum\limits_{i \ne j} {{w_{ij}}{d_{ij}}} } \right)/\left( {\sum\limits_{i \ne j} {{w_{ij}}{\mathit{\Theta }_{ij}}} } \right)$
|
(27) |
2 实验和结果分析
为了验证本文提出的球面嵌入算法的正确性,文中设计了两类模拟数据进行测试,一类是球面均匀分布的数据集,另一类是球面正态分布的数据集。下面将在2.1节中详细介绍产生这两类模拟数据的过程,在2.2节中详细介绍实验过程和评价结果。
2.1 模拟数据的产生
下面介绍两类模拟数据集:球面均匀分布的数据集和球面正态分布的数据集的产生过程。
2.1.1 球面均匀分布的模拟数据集
每个样本点可表示为xi=(θi,φi),i=1,2,…,N,其中θi∈[0,π],φi∈[0,2π],N为样本总数。首先模拟产生了随机均匀分布于单位球面的N=2 000个样本,然后利用式(2) 计算出这些样本两两间的夹角Θij,设半径r为0.5,利用式(1) ,即可得到均匀分布于半径为0.5的球面上的数据对应的距离矩阵。
2.1.2 球面正态分布的模拟数据集
本实验用Kent分布[17]模拟产生了位于单位球面上的正态分布数据。这个数据集(N=913) 主要由三部分组成,一部分是呈圆形的正态分布,另两部分都是呈椭圆形的正态分布,而且这两个椭圆形分布的数据,其分布大小和密度都不同。之后,得到一个分布于半径为2的球面上的包含3个不同Kent分布的数据集对应的距离矩阵。
2.2 实验结果
在实验中,先取每个样本点和其前nn(nn∈[0,N])个近邻点的距离构成稀疏距离矩阵,将此作为球面嵌入算法的输入。算法的输出为所有样本点在单位球面上的坐标。通过此坐标可以计算出嵌入单位球面空间后样本点间的夹角Θij,然后利用式(27) 计算出适合原始数据分布的球面半径R。最后以均方根误差(Root Mean Square Error,RMSE)为指标,衡量所有的原始数据两两间的夹角dij/r与嵌入球面后对应的数据两两间的夹角Θij间的误差,见式(28) 。用近邻均方根误差(Root Mean Square Error between Nearest Neighbors,NN_RMSE)来表示原始数据的近邻点间的夹角与嵌入球面后对应的夹角之间的误差,见式(29) 。另外,半径的估算误差(Radius estimation Error,R_Error)计算见式(30) 。
|
$RMSE = \sqrt {\frac{1}{{{N^2}}}\sum\limits_{i,j = 1}^N {{{\left( {{d_{ij}}/r - {\mathit{\Theta }_{ij}}} \right)}^2}} } $
|
(28) |
|
$NN\_MSE = \sqrt {\frac{1}{{\sum\limits_{i,j = 1}^N {{w_{ij}}} }}\sum\limits_{i,j = 1}^N {{w_{ij}}{{\left( {{d_{ij}}/r - {\mathit{\Theta }_{ij}}} \right)}^2}} } $
|
(29) |
|
$R\_Error = \left| {R - r} \right|$
|
(30) |
若这三个值越小,则说明将样本嵌入球面空间的效果越好。
对于球面均匀分布的数据集,设置近邻点个数nn={N,0.75N,0.5N,0.25N,0.05N}进行实验,由于该算法的初始化是随机的,因此在每个参数设置下同一个实验都重复运行3次。最后,对于半径为r=0.5的数据的实验结果汇总于表 1。
表 1
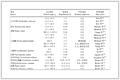
表 1 嵌入算法对两类模拟数据的处理结果
Table 1 Processing results of two kinds of simulated data by the proposed embedding algorithm
|
数据 | 近邻数nn | 误差 | 第一次 | 第二次 | 第三次
|
球面
均匀
分布 |
2 000 |
NN_RMSE | 1.90E-10 | 1.93E-10 | 1.96E-10 |
|
RMSE | 1.90E-10 | 1.93E-10 | 1.96E-10 |
|
R_Error | 4.05E-15 | 4.03E-14 | 1.90E-14 |
|
1 500 |
NN_RMSE | 2.24E-10 | 2.19E-10 | 3.65E-02 |
|
RMSE | 1.95E-10 | 1.91E-10 | 4.19E-02 |
|
R_Error | 1.18E-14 | 1.74E-14 | 2.24E-04 |
|
1 000 |
NN_RMSE | 2.72E-10 | 2.72E-10 | 2.68E-10 |
|
RMSE | 1.94E-10 | 1.94E-10 | 1.91E-10 |
|
R_Error | 7.88E-15 | 2.57E-14 | 1.45E-13 |
|
500 |
NN_RMSE | 6.30E-10 | 3.79E-10 | 3.74E-08 |
|
RMSE | 5.58E-10 | 1.91E-10 | 4.19E-08 |
|
R_Error | 3.50E-13 | 4.16E-13 | 1.48E-10 |
|
100 |
NN_RMSE | 2.48E-05 | 2.14E-05 | 6.09E-07 |
|
RMSE | 9.80E-05 | 9.09E-05 | 2.64E-06 |
|
R_Error | 1.25E-06 | 9.55E-07 | 2.99E-08 |
球面
正态
分布
|
913 |
NN_RMSE | 6.89E-02 | 2.81E-10 | 3.12E-02 |
|
RMSE | 6.89E-02 | 2.81E-10 | 3.12E-02 |
|
R_Error | 5.43E-04 | 2.71E-10 | 3.62E-05 |
|
700 |
NN_RMSE | 5.69E-02 | 1.27E-01 | 9.90E-02 |
|
RMSE | 5.81E-02 | 1.28E-01 | 1.01E-01 |
|
R_Error | 3.07E-04 | 4.75E-04 | 6.31E-04 |
|
500 |
NN_RMSE | 7.08E-02 | 1.06E-01 | 8.33E-02 |
|
RMSE | 7.92E-02 | 1.26E-01 | 9.40E-02 |
|
R_Error | 9.90E-03 | 1.30E-02 | 1.14E-02 |
|
300
|
NN_RMSE | 1.13E-01 | 6.28E-02 | 1.10E-01 |
|
RMSE | 4.02E-01 | 3.31E-01 | 4.02E-01 |
|
R_Error | 2.63E-01 | 1.76E-01 | 2.56E-01
|
|
表 1 嵌入算法对两类模拟数据的处理结果
Table 1 Processing results of two kinds of simulated data by the proposed embedding algorithm
|
从表 1中可以看出,针对不同的近邻点个数设置,本文提出的嵌入算法都能得到较准确的结果,所有的均方根误差(RMSE)基本都小于0.000 01,并且,当每个样本点拥有的近邻点数目越多,则算法嵌入的效果越好,得到的整体数据在单位球面上的分布与原始空间中的分布的一致性也越高。
另外,对于半径r=3.2 的球面均匀分布的数据也做了相同的实验,并得到了类似的测试结果。可见对均匀分布于球面的数据,该算法即使在非近邻点间距离信息缺失较多的情况下,仍然能够较准确地还原出球面空间中数据的分布结构;而且算法还可以较精确地估算出适合数据分布的球面半径。
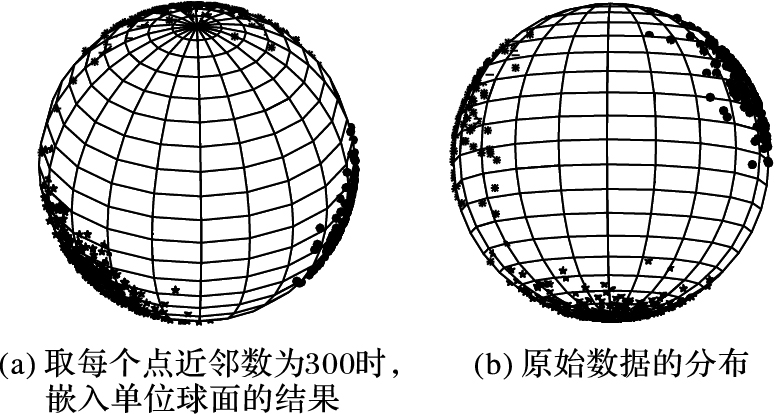
接着,对球面正态分布(Kent分布)的数据也进行了类似的测试,其球面半径的设置为r=2,并取近邻点个数nn={N,700,500,300},在每个参数设置下都重复运行3次,实验结果见表 1。在nn=300时,第一次运行的球面嵌入结果如图 1(a)所示。作为参照,图 1(b)显示了原始数据的分布。
实验结果表明,对于球面正态分布的数据,从图 1和表 1都可以看出,其嵌入球面后的整体分布与原始分布比较接近,但是,整体嵌入后的误差都明显比表 1中球面均匀分布数据的误差大很多。另外,随着近邻点数目的减少,算法将其嵌入单位球面空间后,虽然可以较好地保持其近邻点结构,但是非近邻点间的分布却与原始数据中的分布相差较大。例如表 1中,对于球面正态分布的数据nn=300时,NN_RMSE都小于0.113,然而RMSE的值则都大于0.331;同时,对于适合原始数据分布的球面半径的估算误差也随近邻数的减小而增大。
此外,由于初始化是随机的,本文提出的算法有时会陷入局部极小,因此导致实验结果的不稳定。例如,表 1中,对于球面均匀分布的数据nn=1 500时,三次运行结果波动很大,第三次实验的运行结果中RMSE和NN_RMSE比前两次对应的误差分别高了8个数量级。另外表 1中,对于球面正态分布的数据nn=913时,第二次运行结果的RMSE和NN_RMSE明显比其他两次运行结果的误差低了8个数量级。所以,为保证实验结果的准确性和正确性,每个实验都要经过多次运算。
3 结语
本文首次提出了一种针对球面半径未知且原始数据间的非近邻距离缺失情况下的球面嵌入算法。该算法能够在只已知近邻点间距离的情况下,将任意尺度的数据嵌入至单位球面,还可以估算出适合原始数据分布的球面半径。
本文提出的算法对于球面均匀分布的数据,在非近邻点间距离信息缺失较多的情况下,仍然能得到较准确的球面嵌入结果;但是,对于非均匀分布的数据,嵌入球面空间后,虽然近邻点间的相对位置可以较好地保持,但是无法准确地还原非近邻点间的相对位置,因此对于非均匀分布的数据,球面嵌入算法还有待改进。