从1963年美国气象学家Lorenz[1]开始研究混沌现象至今,已有40多年的历史,已成为理解和运用丰富的动力学的一种常见理念,它是一种对初始条件、参数变量、环境噪声等因素相当敏感的非线性动态系统,基于系统的不确定性与敏感特性,对于混沌系统的同步控制,越来越多的研究者开始进行深入探讨研究,将许多控制理论与技术应用于混沌控制中[2-4],旨在消除系统非线性控制中出现的混沌现象。例如:文献[5]中提出脉冲同步控制;文献[6]中介绍H∞同步控制;文献[7]中引入状态观测器实现同步控制;文献[8]中运用线性矩阵不等式技术达到同步控制;文献[9-10]中设计滑模控制器完成同步控制;文献[10-11]中阐述反推式线性算法的同步控制;文献[12-13]中说明了模糊逻辑的同步控制。同时,随着Pecora等[14]对混沌现象的开创性工作的进行,混沌控制的研究理论与技术被广泛应用于医药科学、生物工程、图像加密、通信安全、信息处理等高科技领域,对现今科技的发展具有深远影响。
其中,在电力电子领域,Kuroe等[15]在1989年将混沌控制引入电动机驱动系统中,指出 永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM) 中混沌现象弊端:电机参量在一定范围内变化时,引起电机转矩随机变化、转速大范围内间歇震荡、不规则的电流噪声、控制性能不稳定等后果,影响了PMSM系统运行的平稳性。现代工业进程中自动化的发展使电动机系统的混沌控制获得越来越多的关注,尤其是PMSM以其效率高、体积小、噪声小、温升低、节能等优势,特别是在目前国家“节能减排”的大环境下,具有极为广阔的应用前景。例如:在电动汽车驱动系统领域,1996年,丰田汽车公司的电动车RAV4就采用了东京电机公司的插入式PMSM作为驱动电机;在电梯领域,国内宁渡欣达公司、山东百斯特电梯有限公司都加大了对PMSM同步无齿轮拽引机的研制;通力公司开发了EcoDiso永磁盘式无齿拽引机;在船舶电力推进领域,西门子开发出了以PMSM为系统方案合作伙伴项目的推进系统。PMSM是高新技术产业强大的技术基础,与电力电子技术和微电子控制技术结合,创造出新型的性能优异的机电一体化产品和装备,是21世纪电机发展方向的风向标,已经有不少学者对永磁同步电动机进行了深入的研究。 例如:文献[16-17]介绍了PMSM的分岔与混沌现象。许多控制理论与技术也被运用在永磁同步电动机的混沌控制中,例如:利用时间延迟反馈技术实现的电动同步机控制[18],利用自适应反推式原理实现的电动机同步控制[19],利用确定的线性化微分几何理论实现的电动机同步控制[20],利用李雅诺夫瞬态指数控制算法实现的电动机同步控制[21],以及利用最优输出反馈H∞技术实现的电动机同步控制[22]等。这些控制方法都实现了PMSM的同步控制,但只能保证平衡点的同步控制,仍存在不能控制非平衡点的缺陷。
以往的研究方法大多考虑不确定参数和外部扰动量的影响,因为在电动机的实际运转过程中,不可避免地存在一些不确定参数和外部扰动量;此外,由于多数控制是使电动机达到平衡点或周期点,不能根据工程需求灵活地调整PMSM的输入输出。针对以上两个缺点,本文以同步误差理论与李雅普诺夫理论为基础,设计了一种新形式的自适应控制器,实现带有不确定参数与外部扰动量的永磁同步电动机的平衡状态控制;运用有限时间原理,证明PMSM在有限时间内的收敛性与稳定性,保证永磁同步电动机在有限时间内快速地达到电动机的预期控制设定值;最后,通过Matlab软件进行数值仿真来验证所设计的自适应控制器的鲁棒性与可行性。
1 PMSM的数学模型及问题阐述经过转换后的均匀气隙的永磁同步电动机的数学模型如下:
| $\left\{ \begin{align} & \frac{d{{i}_{d}}}{dt}=-{{i}_{d}}+w{{i}_{q}}+{{u}_{d}} \\ & \frac{d{{i}_{q}}}{dt}=-{{i}_{q}}-w{{i}_{d}}+\gamma w+{{u}_{q}} \\ & \frac{dw}{dt}=\sigma \left( {{i}_{q}}-w \right)-{{T}_{L}} \\ \end{align} \right.$ | (1) |
系统(1) 中id、iq、w是系统的状态变量;id、iq分别表示定子电流在纵轴和正交轴上的分量电流;w表示电机的转子角速度;ud、uq表示定子电压在纵轴和正交轴上的分量电压;TL表示负载的转矩;γ、σ表示系统参量。
在实际的PMSM模型中,系统参量γ、σ具有不确定性,诸如分岔和混沌等现代非线性理论已经被应用在系统(1) 中非线性动态性能的研究中,研究结果表明,系统参量γ、σ在一定范围内变动,混沌现象出现在PMSM中,在文献[16]中详细地介绍了分岔的尺度标准,一般情况下,考虑PMSM没有外力的情形,此时可以看作PMSM是空载运行一段时间后突然断电,各项外部输入为零,即ud=uq=TL=0,系统模型变为:
| $\left\{ \begin{align} & \frac{d{{i}_{d}}}{dt}=-{{i}_{d}}+w{{i}_{q}} \\ & \frac{d{{i}_{q}}}{dt}=-{{i}_{q}}-w{{i}_{d}}+\gamma w \\ & \frac{dw}{dt}=\sigma \left( {{i}_{q}}-w \right) \\ \end{align} \right.$ | (2) |
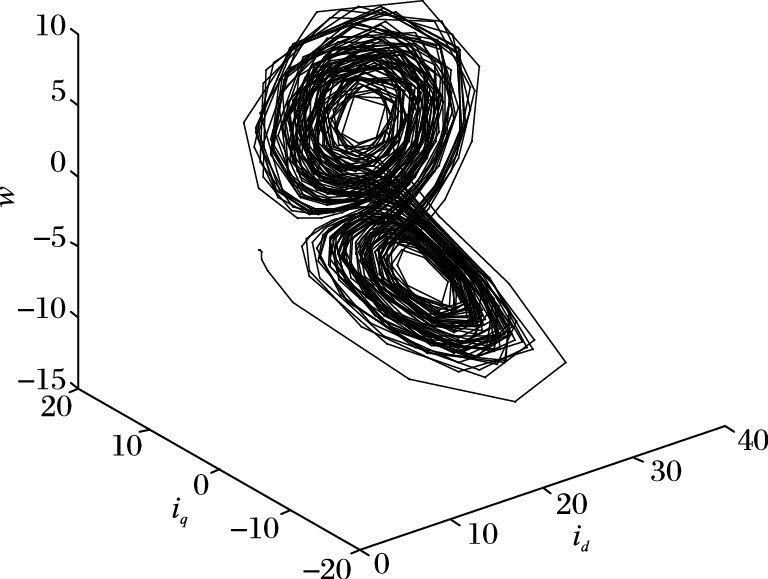
系统(2) 出现混沌现象,此时令γ=20,σ=5.46,id(0) =5 A, iq(0) =1 A,w(0) =-1 rad/s,其仿真的三维混沌吸引子如图 1所示。
|
图 1 PMSM的奇异吸引子 Figure 1 Singular attractor of PMSM |
从图 1中可知,混沌吸引子的存在会严重影响PMSM的正常运转,甚至导致传动系统崩溃,本文旨在用有效灵活的方法抑制PMSM的混沌现象。
设id0、iq0、w0分别为系统(2) 的id、iq、w的预期控制设定值,令e1=id-id0,e2=iq-iq0,e3=w-w0,得到相应的误差系统:
| $\left\{ \begin{align} & {{{\dot{e}}}_{1}}=-{{e}_{1}}+{{e}_{2}}{{e}_{3}}+{{w}_{0}}{{e}_{2}}+{{i}_{q0}}{{e}_{3}}+{{u}_{1}} \\ & {{{\dot{e}}}_{2}}=-{{e}_{2}}-{{e}_{1}}{{e}_{3}}+\gamma {{e}_{3}}-{{w}_{0}}{{e}_{1}}-{{i}_{d0}}{{e}_{3}}+a+{{u}_{2}} \\ & {{{\dot{e}}}_{3}}=\sigma ({{e}_{2}}-{{e}_{3}})+{{u}_{2}} \\ \end{align} \right.$ | (3) |
其中:a=-iq0-w0id0+γw0;u1、u2、u3分别是误差系统(3) 的控制输入。
引理1 Barbalat引理[23]。设f: [0,∞)→R一阶可导,且t→∞时极限存在,如果
引理2 Jensen引理[24]。设xi≥0(1≤i≤n),则有以下不等式成立:(x1c1+x2c1+x3c1+…+xnc1)1c1≤(x1c2+x2c2+x3c2+…+xnc2)1c2。
引理3[25] 设定一个动态非线性系统:
如果存在三个连续可微函数
| $\begin{align} & V(t,0)=0,t\in \left[ 0,\infty \right) \\ & \alpha \left( \left\| x \right\| \right)\le V(t,x)\le \beta \left( \left\| x \right\| \right),t\in \left[ 0,\infty \right),x\in M \\ & \dot{V}(t,x)\le -k(t){{(V(t,x))}^{\lambda }};t\in \left[ 0,\infty \right),x\in M \\ \end{align}$ |
那么,当时间函数
引理4[26] 设定一个动态非线性系统
定义1 基于电磁同步电动机系统(2) 构造的电磁同步电动机误差系统(3) ,在自适应控制器和自适应矫正律的作用下,如果存在一个常数T(T≥0) ,误差系统(3) 达到状态:
| $\underset{t\to T}{\mathop{\lim }}\,{{\left\| \mathit{\boldsymbol{e}} \right\|}_{i}}=0;(i=1,2,3)$ | (4) |
且当t≥T时,‖e(t)‖=0,则电磁同步电动机误差系统(3) 在有限时间T或大于等于T内可以实现混沌控制,即保证电磁同步电动机系统(2) 在T或大于等于T内达到电动机的预期控制设定值并维持平衡状态下正常运转,实现电动机的混沌控制。
2 自适应控制的实现为确保PMSM能在有限时间内快速收敛到电动机的预期控制设定值,并维持平衡状态下系统(2) 的正常运转,最终抑制PMSM中的混沌现象,本文设计自适应控制器的数学模型如下所示:
| $\left\{ \begin{align} & {{u}_{1}}=-{{k}_{1}}sign({{e}_{1}})\mathop{\left| {{e}_{1}} \right|}^{\alpha } \\ & {{u}_{2}}=-{{k}_{2}}sign({{e}_{2}})\mathop{\left| {{e}_{2}} \right|}^{\alpha }-\hat{\gamma }{{e}_{3}}-a \\ & {{u}_{3}}=-{{k}_{3}}sign({{e}_{3}})\mathop{\left| {{e}_{3}} \right|}^{\alpha }-\hat{\sigma }({{e}_{2}}-{{e}_{3}})-({{i}_{q0}}{{e}_{1}}-{{i}_{d0}}{{e}_{2}}) \\ \end{align} \right.$ | (5) |
其中:ki>0(i=1,2,3) ;0 <α<1;
γ、σ是电磁同步电动机中的可操作参量,故设计校正律的数学模型如下所示:
| $\left\{ \begin{align} & \dot{\hat{\gamma }}={{e}_{2}}{{e}_{3}} \\ & \dot{\hat{\sigma }}={{e}_{2}}{{e}_{3}}-{{e}_{3}}^{2} \\ \end{align} \right.$ | (6) |
证明 选取正定的李雅普诺夫函数:
| $V=\frac{1}{2}e_{1}^{2}+\frac{1}{2}e_{2}^{2}+\frac{1}{2}e_{3}^{2}+\frac{1}{2}{{\tilde{\gamma }}^{2}}+\frac{1}{2}{{\tilde{\sigma }}^{2}}$ | (7) |
对式(7) 求导可得:
| $\dot{V}={{e}_{1}}{{\dot{e}}_{1}}+{{e}_{2}}{{\dot{e}}_{2}}+{{e}_{3}}{{\dot{e}}_{3}}-\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }}$ | (8) |
将式(3) 代入式(8) 可得:
| $\begin{align} & \dot{V}={{e}_{1}}(-{{e}_{1}}+{{e}_{2}}{{e}_{3}}+{{w}_{0}}{{e}_{2}}+{{i}_{q0}}{{e}_{3}}+{{u}_{1}}) \\ & \text{ }+{{e}_{2}}\left( -{{e}_{2}}-{{e}_{1}}{{e}_{3}}+\gamma {{e}_{3}}-{{w}_{0}}{{e}_{1}}-{{i}_{d0}}{{e}_{3}}+{{u}_{2}} \right) \\ & \text{ }+{{e}_{3}}\left( \sigma ({{e}_{2}}-{{e}_{3}})+{{u}_{3}} \right)-\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }} \\ \end{align}$ | (9) |
对式(9) 进行化简:
| $\begin{align} & \dot{V}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-\sigma {{e}_{3}}^{2}+a{{e}_{2}}+{{i}_{q0}}{{e}_{1}}{{e}_{3}}-{{i}_{d0}}{{e}_{2}}{{e}_{3}}+(\gamma +\sigma ){{e}_{2}}{{e}_{3}} \\ & \text{ }+{{e}_{1}}{{u}_{1}}+{{e}_{2}}{{u}_{2}}+{{e}_{3}}{{u}_{3}}\text{+}\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }} \\ \end{align}$ | (10) |
将自适应控制器(5) 代入式(10) 可得:
| $\begin{align} & \dot{V}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-\sigma {{e}_{3}}^{2}+a{{e}_{2}}+{{i}_{q0}}{{e}_{1}}{{e}_{3}}-{{i}_{d0}}{{e}_{2}}{{e}_{3}} \\ & \text{ }+(\gamma +\sigma ){{e}_{2}}{{e}_{3}}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \text{ }-a{{e}_{2}}-{{i}_{q0}}{{e}_{1}}{{e}_{3}}+{{i}_{d0}}{{e}_{2}}{{e}_{3}}-\left( \hat{\gamma }+\hat{\sigma } \right){{e}_{2}}{{e}_{3}}-\hat{\sigma }{{e}_{3}}^{2}-\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }} \\ \end{align}$ | (11) |
将
| $\begin{align} & \dot{V}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-\tilde{\sigma }{{e}_{3}}^{2}+\left( \tilde{\gamma }+\tilde{\sigma } \right){{e}_{2}}{{e}_{3}}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1} \\ & \text{ }-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1}-\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }} \\ \end{align}$ | (12) |
将自适应校正律(6) 代入式(12) 可得:
| $\begin{align} & \dot{V}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-\tilde{\sigma }{{e}_{3}}^{2}+\left( \tilde{\gamma }+\tilde{\sigma } \right){{e}_{2}}{{e}_{3}}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1} \\ & \text{ }-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1}-\tilde{\gamma }{{e}_{2}}{{e}_{3}}-\tilde{\sigma }\left( {{e}_{2}}{{e}_{3}}-{{e}_{3}}^{2} \right) \\ \end{align}$ | (13) |
对式(13) 进行化简:
| $\dot{V}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1}\le 0$ | (14) |
由式(14) 可得:
| $V(t)\le V(0)$ | (15) |
即:
| $V(t)=\frac{1}{2}e_{1}^{2}+\frac{1}{2}e_{2}^{2}+\frac{1}{2}e_{3}^{2}+\frac{1}{2}{{\tilde{\gamma }}^{2}}+\frac{1}{2}{{\tilde{\sigma }}^{2}}\le V(0)$ | (16) |
由此,自适应控制器(5) 保证了解决方案
设定初始状态,e1(0) =e2(0) =e3(0) =0,式(16) 化简可得:
| ${{\tilde{\gamma }}^{2}}+{{\tilde{\sigma }}^{2}}\le 2V(0)$ | (17) |
设定下列式子:
| ${{V}_{1}}=\frac{1}{2}e_{1}^{2}+\frac{1}{2}e_{2}^{2}+\frac{1}{2}e_{3}^{2}$ | (18) |
由式(12) 可知:
| $\begin{align} & {{{\dot{V}}}_{1}}=-{{e}_{1}}^{2}-{{e}_{2}}^{2}-\tilde{\sigma }{{e}_{3}}^{2}+\left( \tilde{\gamma }+\tilde{\sigma } \right){{e}_{2}}{{e}_{3}}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1} \\ & \text{ }-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ \end{align}$ | (19) |
假定:
| $\begin{align} & {{{\dot{V}}}_{11}}=-{{e}_{2}}^{2}-\tilde{\sigma }{{e}_{3}}^{2}+\left( \tilde{\gamma }+\tilde{\sigma } \right){{e}_{2}}{{e}_{3}}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & {{{\dot{V}}}_{11}}\le -{{e}_{2}}^{2}-\tilde{\sigma }{{e}_{3}}^{2}+\frac{{{\left( \tilde{\gamma }+\tilde{\sigma } \right)}^{2}}{{e}_{3}}^{2}}{4}+{{e}_{2}}^{2}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & =-\tilde{\sigma }{{e}_{3}}^{2}+\frac{{{\left( \tilde{\gamma }+\tilde{\sigma } \right)}^{2}}{{e}_{3}}^{2}}{4}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \le \left( \frac{{{{\tilde{\gamma }}}^{2}}+{{{\tilde{\sigma }}}^{2}}}{2}+\left| {\tilde{\sigma }} \right| \right){{e}_{3}}^{2}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \le \left( \left( V(0)+\sqrt{2V(0)} \right){{\left| {{e}_{3}} \right|}^{1-\alpha }}-\frac{{{k}_{3}}}{2} \right)\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ \end{align}$ | (20) |
由分析可知,当e3满足条件
| $\left| {{e}_{3}} \right|\le {{\left( \frac{{{k}_{3}}}{2\left( V(0)+\sqrt{2V(0)} \right)} \right)}^{{}^{1}\!\!\diagup\!\!{}_{1-\alpha }\;}}$ |
时,
根据Jensen引理可知:
| $\begin{align} & {{(\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}+\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}+\mathop{\left| {{e}_{3}} \right|}^{\alpha +1})}^{\frac{1}{\alpha +1}}} \\ & \ge {{(\mathop{\left| {{e}_{1}} \right|}^{2}+\mathop{\left| {{e}_{2}} \right|}^{2}+\mathop{\left| {{e}_{3}} \right|}^{2})}^{\frac{1}{2}}}={{\left( 2{{V}_{1}} \right)}^{0.5}} \\ \end{align}$ | (21) |
由式(16) 化简式(18) :
| $\begin{align} & {{{\dot{V}}}_{1}}\le -{{e}_{1}}^{2}-{{e}_{2}}^{2}-{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \text{ }\le -{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-\frac{{{k}_{3}}}{2}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \text{ }\le -{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1} \\ & \text{ }\le -\min \left\{ {{k}_{1}},{{k}_{2}},{{k}_{3}} \right\}{{\left( \mathop{\left| {{e}_{1}} \right|}^{2}+\mathop{\left| {{e}_{2}} \right|}^{2}+\mathop{\left| {{e}_{3}} \right|}^{2} \right)}^{\frac{\alpha +1}{2}}} \\ & \text{ }=-\min \left\{ {{k}_{1}},{{k}_{2}},{{k}_{3}} \right\}{{\left( 2{{V}_{1}} \right)}^{\frac{\alpha +1}{2}}} \\ \end{align}$ | (22) |
根据引理可知,对于任意
| $\begin{align} & ({{e}_{1}},{{e}_{2}},{{e}_{3}},\hat{\gamma },\hat{\sigma },\tilde{\gamma },\tilde{\sigma })\in \Omega = \\ & \left\{ {{\left( 2{{V}_{1}} \right)}^{0.5}}\le {{\left( \frac{{{k}_{3}}}{2\left( V(0)+\sqrt{2V(0)} \right)} \right)}^{{}^{1}\!\!\diagup\!\!{}_{1-\alpha }\;}} \right\} \\ & {{{\dot{V}}}_{1}}\le -\min \left\{ {{k}_{1}},{{k}_{2}},{{k}_{3}} \right\}{{\left( 2{{V}_{1}} \right)}^{\frac{\alpha +1}{2}}} \\ \end{align}$ |
所以当初始条件满足:
| $\begin{align} & ({{e}_{1}}(0),{{e}_{2}}(0),{{e}_{3}}(0),\hat{\gamma }(0),\hat{\sigma }(0),\tilde{\gamma }(0),\tilde{\sigma }(0))\in \Omega \\ & {{{\dot{V}}}_{1}}\le -\min \left\{ {{k}_{1}},{{k}_{2}},{{k}_{3}} \right\}{{\left( 2{{V}_{1}} \right)}^{\frac{\alpha +1}{2}}} \\ \end{align}$ |
根据引理3可知,对于t=0时的误差系统(3) 是局部一致有限时间稳定,进而再根据引理4可知,误差系统(3) 在控制输入(5) 在作用下,(e1(0) ,e2(0) ,e3(0) )=(0,0,0) 时是全局有限时间自适应稳定。
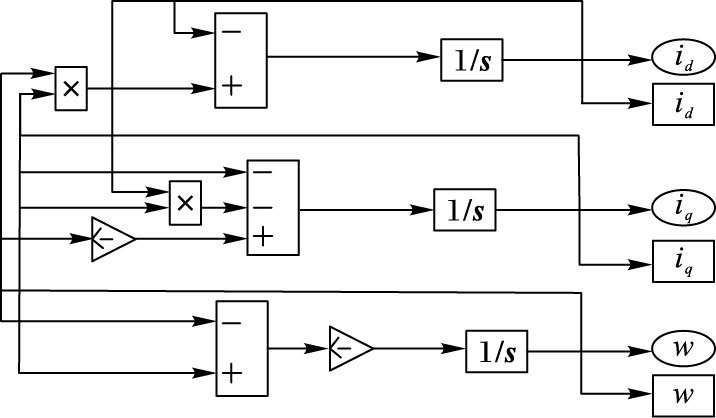
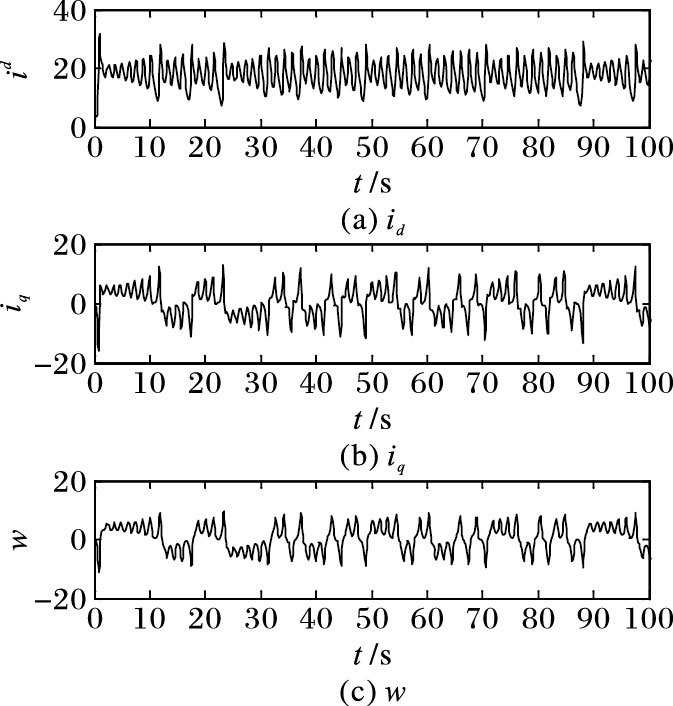
3 仿真结果与分析为验证本文所提出的控制方法的有效性,通过Matlab软件中的Simulink模块搭建PMSM模型如图 2所示,对该同步控制方法进行数值仿真。当设定γ=20,σ=5.46时,永磁同步电动机出现混沌现象,令初始条件为id(0) =5 A,iq(0) =1 A, w(0) =-1 rad/s,PMSM的各状态变量随时间变化的状态如图 3所示。
|
图 2 PMSM的Simulink模型 Figure 2 Simulink model of PMSM |
|
图 3 PMSM的状态变量 Figure 3 State variables of PMSM |
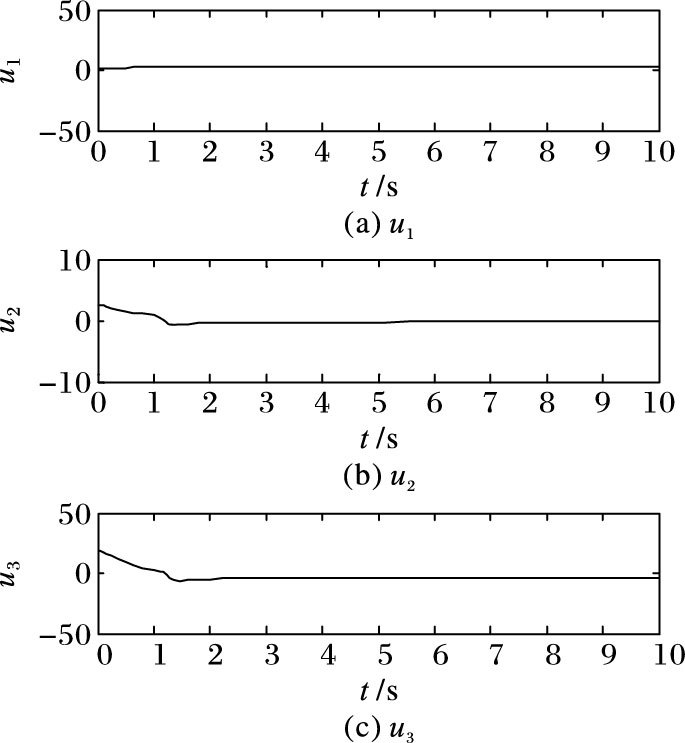
此时,设定控制器中各参量值:k1=1.8,k2=3,k3=5,α=0.5,校正率中参量初始值:
|
图 4 控制输入的时间状态 Figure 4 Time state of control input |
|
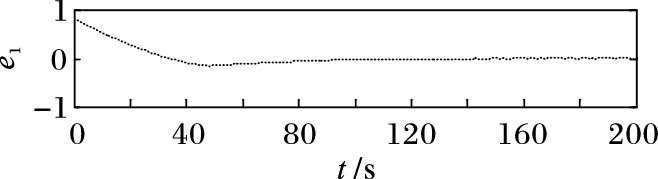
图 5 误差状态变量e1=id-id0 Figure 5 Error state variable of e1=id-id0 |

|
图 6 误差状态变量e2=iq-iq0 Figure 6 Error state variable of e2=iq-iq0 |
|
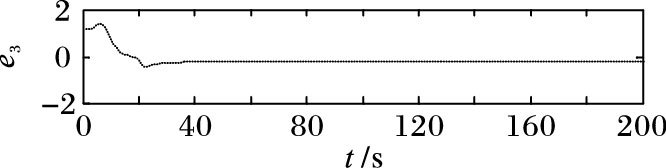
图 7 误差状态变量e3=w-w0 Figure 7 Error state variable of e3=w-w0 |
在一个闭环系统中,不可避免地会出现外部干扰,在外部干扰量的作用下,本文的同步控制方法同样可以使PMSM在有限时间内快速地达到电动机的预期控制设定值,并维持在平衡状态运转。考虑到外部干扰量,建立如下PMSM模型:
| $\left\{ \begin{align} & {{{\dot{e}}}_{1}}=-{{e}_{1}}+{{e}_{2}}{{e}_{3}}+{{w}_{0}}{{e}_{2}}+{{i}_{q0}}{{e}_{3}} \\ & \text{ }+\text{ }{{f}_{1}}\left( t \right)-{{k}_{1}}sign({{e}_{1}})\mathop{\left| {{e}_{1}} \right|}^{\alpha } \\ & {{{\dot{e}}}_{2}}=-{{e}_{2}}-{{e}_{1}}{{e}_{3}}+\gamma {{e}_{3}}-{{w}_{0}}{{e}_{1}}-{{i}_{d0}}{{e}_{3}} \\ & \text{ }+{{f}_{2}}\left( t \right)-{{k}_{2}}sign({{e}_{2}})\mathop{\left| {{e}_{2}} \right|}^{\alpha }-\hat{\gamma }{{e}_{3}} \\ & {{{\dot{e}}}_{3}}=\sigma ({{e}_{2}}-{{e}_{3}})+{{f}_{3}}\left( t \right)-{{k}_{3}}sign({{e}_{3}})\mathop{\left| {{e}_{3}} \right|}^{\alpha } \\ & \text{ }-\hat{\sigma }({{e}_{2}}-{{e}_{3}})-{{e}_{3}}-({{i}_{q0}}{{e}_{1}}-{{i}_{d0}}{{e}_{2}}) \\ \end{align} \right.$ | (23) |
外部扰动量为:
| $\left\{ \begin{align} & {{f}_{1}}\left( t \right)=0.01sin(100{{i}_{d}}) \\ & {{f}_{2}}\left( t \right)=0.01sin(100{{i}_{q}}) \\ & {{f}_{3}}\left( t \right)=0.01sin(100w) \\ \end{align} \right.$ | (24) |
证明
| $V=\frac{1}{2}e_{1}^{2}+\frac{1}{2}e_{2}^{2}+\frac{1}{2}e_{3}^{2}+\frac{1}{2}{{{\tilde{\gamma }}}^{2}}+\frac{1}{2}{{{\tilde{\sigma }}}^{2}}$ |
因为:
| ${{i}_{d}}{{f}_{1}}\le {{i}_{d}}^{2},{{i}_{q}}{{f}_{2}}\le {{i}_{q}}^{2},w{{f}_{3}}\le {{w}^{2}}$ |
所以:
| $\begin{align} & \dot{V}={{e}_{1}}{{{\dot{e}}}_{1}}+{{e}_{2}}{{{\dot{e}}}_{2}}+{{e}_{3}}{{{\dot{e}}}_{3}}-\tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\dot{\hat{\sigma }} \\ & \text{ }={{e}_{1}}(-{{e}_{1}}+{{e}_{2}}{{e}_{3}}+{{w}_{0}}{{e}_{2}}+{{i}_{q0}}{{e}_{3}}+{{f}_{1}}-{{k}_{1}}sign({{e}_{1}})\mathop{\left| {{e}_{1}} \right|}^{\alpha })+ \\ & \text{ }{{e}_{2}}\left( -{{e}_{2}}-{{e}_{1}}{{e}_{3}}+\gamma {{e}_{3}}-{{w}_{0}}{{e}_{1}}-{{i}_{d0}}{{e}_{3}}+{{f}_{2}}- \right. \\ & \text{ }\left. {{k}_{2}}sign({{e}_{2}})\mathop{\left| {{e}_{2}} \right|}^{\alpha }-\hat{\gamma }{{e}_{3}}_{2} \right)+{{e}_{3}}\left( \sigma ({{e}_{2}}-{{e}_{3}})+{{f}_{3}}- \right. \\ & \left. {{k}_{3}}sign({{e}_{3}})\mathop{\left| {{e}_{3}} \right|}^{\alpha }-\hat{\sigma }({{e}_{2}}-{{e}_{3}})-{{e}_{3}}-({{i}_{q0}}{{e}_{1}}-{{i}_{d0}}{{e}_{2}}) \right)- \\ & \tilde{\gamma }\dot{\hat{\gamma }}-\tilde{\sigma }\hat{\sigma }\le -{{k}_{1}}\mathop{\left| {{e}_{1}} \right|}^{\alpha +1}-{{k}_{2}}\mathop{\left| {{e}_{2}} \right|}^{\alpha +1}-{{k}_{3}}\mathop{\left| {{e}_{3}} \right|}^{\alpha +1}\le 0 \\ \end{align}$ |
同理可知,PMSM在受到温度、气压、白噪声等外部扰量的影响下,用本文所提出的控制方法仍可以有效地在平衡状态下稳定运转,实现电动机的快速同步控制,保证了PMSM具有良好的鲁棒性能。
5 结语综上所述,自适应控制器配合校正率的使用有效地抑制了PMSM中产生混沌吸引子的现象,强有力地保证了PMSM短时间内达到电动机的预期控制设定值,并在该设定值状态下稳定正常运转,对未知参数具有良好的动态响应,对外部干扰量引起的大幅度抖振具有良好的鲁棒特性,最终实现带有不确定参数与外部扰动量的PMSM同步控制的平衡状态。
| [1] | LORENZ E. Deterministic nonperiodic flow[J]. Journal of the Atmospheric Sciences, 1963, 20 (2) : 130-141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [2] | JU H P, JI D H, WON S C, et al. H∞ synchronization of time-delayed chaotic systems[J]. Applied Mathematics & Computation, 2008, 204 (1) : 170-177. |
| [3] | 王银河, 高子林, 王钦若, 等. 基于自适应模糊逻辑系统的一类混沌系统同步控制[J]. 控制与决策, 2013, 28 (9) : 1309-1314. ( WANG Y H, GAO Z L, WANG Q R, et al. Synchronous control in a class of chaotic systems of adaptive fuzzy logic system[J]. Control and Decision, 2013, 28 (9) : 1309-1314. ) |
| [4] | CHEN X, JING Z, FU X. Chaos control in a pendulum system with excitations and phase shift[J]. Nonlinear Dynamics, 2014, 78 (1) : 317-327. doi: 10.1007/s11071-014-1441-y |
| [5] | LIU X G, ZHEN Y X, MAN F H. Projective synchronization in drive response networks via impulsive control[J]. Chinese Physics Letters, 2008, 25 (8) : 2816-2819. doi: 10.1088/0256-307X/25/8/023 |
| [6] | LIN T C, HSU K W. A new adaptive H∞ control for chaos synchronization between two different chaotic systems[J]. International Journal of Innovative Computing, Information and Control, 2012, 8 (1) : 701-714. |
| [7] | 王兴元, 段朝锋. 基于线性状态观测器的混沌同步及其在保密通信中的应用[J]. 通信学报, 2005, 26 (6) : 105-111. ( WANG X Y, YIN C F. Based on the chaotic synchronization of the linear state observer and its application in secret communication[J]. Journal on Communications, 2005, 26 (6) : 105-111. ) |
| [8] | RAFIKOV M, BALTHAZAR J M. On control and synchronization in chaotic and hyper chaotic systems via linear feedback control[J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13 (7) : 1246-1255. doi: 10.1016/j.cnsns.2006.12.011 |
| [9] | ZHANG X, LIU X, ZHU Q. Adaptive chatter free sliding mode control for a class of uncertain chaotic systems[J]. Applied Mathematics & Computation, 2014, 232 : 431-435. |
| [10] | VAIDYANATHAN S. Global chaos synchronization of duffing double-well chaotic oscillators via integral sliding mode control[J]. International Journal of Chemtech Research, 2015, 8 (11) : 141-151. |
| [11] | GALLEGOS J A. Nonlinear regulation of a Lorenz system by feedback linearization techniques[J]. Dynamics & Control, 1994, 4 (4) : 277-298. |
| [12] | MIKKILI S, PANDA A K. Fuzzy logic in control systems:fuzzy logic controller-part 2[J]. International Journal of Emerging Electric Power Systems, 2015, 20 (4) : 419-35. |
| [13] | PAI N S, YAU H T, KUO C L. Comments on "fuzzy logic combining controller design for chaos control of a rod-type plasma torch system"[J]. Expert Systems with Applications, 2010, 37 (12) : 8278-8283. doi: 10.1016/j.eswa.2010.05.057 |
| [14] | PECORA L M, CARROLL T L. Synchronization of chaotic systems[J]. Physical Review Letters, 1990, 64 (8) : 821-824. doi: 10.1103/PhysRevLett.64.821 |
| [15] | KUROE Y, HAYASHI S. Analysis of bifurcation in power electronic induction motor drive systems[C]//Proceedings of the 1989 Power Electronics Specialists Conference, 1989. Piscataway, NJ:IEEE, 1989:923-930. |
| [16] | 夏非, 范莉, 王绍夫. 永磁同步发电机分岔及双参数特性分析[J]. 电源技术, 2012, 36 (12) : 1904-1906. ( XIA F, FAN L, WANG S F. Bifurcation and double parameters characteristics analysis of permanent magnet synchronous motor[J]. Chinese Journal of Power Source, 2012, 36 (12) : 1904-1906. ) |
| [17] | 任海鹏, 刘丁, 李洁. 永磁同步电动机中混沌运动的延迟反馈控制[J]. 中国电机工程学报, 2003, 23 (6) : 175-178. ( REN H P, LIU D, LI J, et al. Delay feedback control of chaos in permanent magnet synchronous motor[J]. China Society Electronic Engineering, 2003, 23 (6) : 175-178. ) |
| [18] | GE X, HUANG J. Chaos control of permanent magnet synchronous motor[C]//Proceedings of the Eighth International Conference on Electrical Machines and Systems. Piscataway, NJ:IEEE, 2005:484-488. |
| [19] | HU J, LIU L, MA D W. Robust nonlinear feedback control of a chaotic permanent-magnet synchronous motor with a load torque disturbance[J]. Journal of the Korean Physical Society, 2014, 65 (12) : 2132-2139. doi: 10.3938/jkps.65.2132 |
| [20] | WEI D Q, LUO X S, WANG B H, et al. Robust adaptive dynamic surface control of chaos in permanent magnet synchronous motor[J]. Physics Letters A, 2007, 363 (1/2) : 71-77. |
| [21] | ZRIBI M, OTEAFY A, SMAOUI N. Controlling chaos in the permanent magnet synchronous motor[J]. Chaos Solitons & Fractals, 2009, 41 (3) : 1266-1276. |
| [22] | 马鸿增, 杨益飞, 骆敏舟, 等. 永磁同步发电机混沌运动分析及最优输出反馈H∞控制[J]. 物理学报, 2015, 64 (4) : 34-40. ( MA H Z, YANG Y F, LUO D Z, et al. Analysis of the chaotic motions of the permanent magnet synchronous generator and the optimal output feedback h-infinity control[J]. Acta Physica Sinica, 2015, 64 (4) : 34-40. ) |
| [23] | WANG J, CHEN X, FU J. Adaptive finite-time control of chaos in permanent magnet synchronous motor with uncertain parameters[J]. Nonlinear Dynamics, 2014, 78 (2) : 1321-1328. doi: 10.1007/s11071-014-1518-7 |
| [24] | DELAVARI H, BALEANU D, SADATI J. Stability analysis of Caputo fractional-order nonlinear systems revisited[J]. Nonlinear Dynamics, 2012, 67 (4) : 2433-2439. doi: 10.1007/s11071-011-0157-5 |
| [25] | HADDAD W M, NERSESOV S G, DU L. Finite-time stability for time-varying nonlinear dynamical systems[C]//Proceedings of the 2008 American Control Conference. Piscataway, NJ:IEEE, 2008:4135-4139. |
| [26] | HONG Y, WANG H O, BUSHNELL L G. Adaptive finite-time control of nonlinear systems[C]//Proceedings of the 2001 American Control Conference. Piscataway, NJ:IEEE, 2001:4149-415. |




