2. 北京理工大学 计算机学院, 北京 100081
2. School of Computer Science & Technology, Beijing Institute of Technology, Beijing 100081, China
随着数字图像和多媒体技术的快速发展,大量的图像被广泛地应用到人类生活中。在这些图像中,有许多包含敏感信息,例如医疗图像、电子支票、军事雷达图像等。因此,需要对这些图像进行保护。当前,许多应用把敏感图像存储在普通服务器或云服务器中。为了保护服务器中的信息,大量的方法被采用,例如在操作系统级进行校验、基于语言的安全策略的执行、应用程序代码静态或动态分析等。尽管采用了这些安全措施,数据泄露事件仍在发生。例如,纽约时报报导,2014年12月,全球金融公司摩根士丹利有大约350 000客户资料被泄露。另一个例子是HeartBleed漏洞,这个漏洞允许攻击者获取系统的安全证书、用户名和密码等敏感信息。当然,还有很多例子表明,在服务器上存储原始数据是不安全的。保护这些敏感图像的一种方法是对存储在服务器上的图像进行加密。这种方法具有很好的应用前景,因为即使攻击者能够攻入服务器,也只能访问被加密过的数据,不能理解明文信息。
经过多年研究,研究人员提出了很多图像加密算法[1-5]。考虑到混沌具有初始条件敏感性、伪随机性、周期性和可再生性等优点,基于混沌的图像加密算法已经成为图像加密领域的一个重要分支。
当前,基于混沌的图像加密可分为三类:即基于空域[6-10]、变换域(频域)[11-16]以及混合域的图像加密[17-18]。基于空域的图像加密算法于1998年由Fridrich首次提出[10];此后,该类加密算法大量涌现。这类加密算法的特征是混乱和扩散都在空间域发生,加密过程不会引入额外的图像变形,因此,被加密的图像保真;然而,这类算法具有弱加密强度、低加密效率等不足[17-18]。基于变换域的图像加密源于光学领域[15],通过对输入平面和傅里叶平面进行随机相位编码获取编码图像用于安全领域;此后,涌现了更多的变换域图像加密算法[11-16]。这类算法的原理是变换域系数的任何改变都会通过逆变换反映在图像的所有像素上。为了改进加密效率,一些算法利用这个原理,仅仅改变部分变换域系数,来实现高效率加密图像的目的。随着基于空域和频域加密算法的出现,基于混合域图像加密算法自然地被提出。这类算法的主要特点是空域和频域都参与到加密算法中,通过频域置乱、空域替换,充分利用空域和频域加密的优点,更好地实现高强度最小扭曲的图像保护。目前有很多这类算法,其中文献[17]提出的算法最具代表性。尽管文献[17]中的算法声称简单、安全,但在置乱和替换部分仍需要改进:算法在置乱部分采用的是分段线性混沌映射,但该映射结构和混沌轨道都非常简单,随着混沌信号估计技术的发展,当提取少量信息时,其混沌方程能够被估计[19-20],参数和初值也可能被预测[21];算法在替换部分仅采用了异或操作,但随着模加操作大量属性被推导,许多对称加密算法被破解[22-23]。
基于这些事实,为了提高基于混合域图像加密算法的抗攻击能力,本文提出了一种新的混合域图像加密算法。该算法的图像置乱部分在小波域实现,并且讨论了小波分解级数,利用混沌魔方变换进行置乱;在空域部分则引入了伽罗瓦域元素乘法和异或混合加密技术;另外还采用了扰动技术来实现一次性运行密钥。实验表明本文提出的图像加密算法具有很强的抗攻击性。
1 基本理论 1.1 二维Sine Logistic调制映射二维Sine Logistic调制映射(Two Dimensional Sine Logistic Modulation Map,2D-SLMM) 方程如下:
| $\left\{ \begin{align} & {{x}_{i+1}}=\alpha \times (sin(\text{ }\!\!\pi\!\!\text{ }{{y}_{i}})+\beta )\times {{x}_{i}}\times (1-{{x}_{i}}) \\ & {{y}_{i+1}}=\alpha \times (sin(\text{ }\!\!\pi\!\!\text{ }{{x}_{i+1}})+\beta )\times {{y}_{i}}\times (1-{{y}_{i}}) \\ \end{align} \right.$ | (1) |
其中:α和β是控制参数,α∈[0,1],β∈[0,3]。
2D-SLMM 由Logistic和Sine 映射推导而来,该混沌动力系统轨道和迭代值难以预测。当参数接近3时,2D-SLMM 呈现出很好的混沌性能[6]。
1.2 2D Logistic映射2D Logistic映射方程[17]如下:
| $\left\{ \begin{align} & {{y}_{n+1}}={{\mu }_{1}}{{y}_{n}}(1-{{y}_{n}})+{{\gamma }_{1}}z_{n}^{2} \\ & {{z}_{n+1}}={{\mu }_{2}}{{z}_{n}}(1-{{z}_{n}})+{{\gamma }_{2}}(y_{n}^{2}+{{y}_{n}}{{z}_{n}}) \\ \end{align} \right.$ |
其中:μ1∈(2.75,3.4],μ2∈(2.75,3.45],γ1∈(0.15,0.21],γ2∈(0.13,0.15],yn,zn∈(0,1) 。
1.3 互绕Logistic映射互绕Logistic映射(intertwining Logistic map)[5]方程如下:
| $\left\{ \begin{align} & {{u}_{n+1}}=[\mu \times {{k}_{1}}\times {{v}_{n}}\times (1-{{u}_{n}})+{{w}_{n}}]mod1 \\ & {{v}_{n+1}}=[\mu \times {{k}_{2}}\times {{v}_{n}}+{{w}_{n}}\times 1/(1+{{({{u}_{n}}_{+1})}^{2}})]\times mod1 \\ & {{w}_{n+1}}=[\mu \times ({{u}_{n+1}}+{{v}_{n+1}}+{{k}_{3}})\times \sin ({{w}_{n}})]\times mod1 \\ \end{align} \right.$ | (2) |
其中:un,vn,wn∈(0,1) ,μ∈(0,3.999],|k1|>33.5, |k2|>37.9, |k3|>35.7。和经典Logistic映射相比,互绕Logistic映射能够克服经典Logistic映射的稳定窗、空白窗、序列的非均匀分布、弱密钥等问题。
1.4 伽罗瓦域元素加法和乘法具有有限数目的域称为有限域或伽罗瓦域,用Fq或GF(q)表示,其中q代表域中元素的数目。域中元素的数目一定是素数或素数的阶数,例如q=p或q=pm,p为素数。本文提出的加密方案采用的伽罗瓦域为GF(256) (GF(28))。该域中元素采用阶数小于8的关于x的多项式表示,多项式的系数位于有限域GF(2) 。GF(2) 只能取{0,1},并进行二进制加法和乘法,但是不能进位,即:1+1=0。
在计算伽罗瓦域GF(256) 中两个元素加法时,采用普通多项式加法运算,只不过计算系数在GF(2) 域中进行。例如:(x4+x3+1) +(x3+x2+1) =x4+x2,这是多项式的正常加法,只不过计算系数发生在GF(2) 域。
在计算伽罗瓦域GF(256) 中两个元素乘法时,首先像普通多项式一样进行乘法运算;接着,把计算的结果除以不可约多项式m(x),比如m(x)=x8+x4+x3+x2+1;然后取余数。例如:
(47) 10×(235) 10=(x5+x3+x2+x+1) × (x7+x6+x5+x3+x+1) mod m(x)=(x12+x11+x7+x5+x3+1) mod m(x)=x7+x6+x4+x3+x=(218) 10
1.5 离散小波变换 1.5.1 基本定义离散小波变换[24]定义为:
| ${{W}_{\varphi }}({{j}_{0}},k)=\frac{1}{\sqrt{K}}\sum\limits_{x}{f(x)}{{\varphi }_{j}}{{_{_{0}}}_{,k}}(x)$ | (3) |
| ${{W}_{\psi }}(j,k)=\frac{1}{\sqrt{K}}\sum\limits_{k}{f(x)}{{\psi }_{j}}_{,k}(x)$ | (4) |
逆离散小波变换定义为:
| $\begin{align} & f(x)=\frac{1}{\sqrt{K}}\sum\limits_{k}{{{W}_{\varphi }}({{j}_{0}},k)}{{\varphi }_{j}}{{_{_{0}}}_{,k}}(x)+ \\ & \frac{1}{\sqrt{K}}\sum\limits_{j={{j}_{0}}}^{\infty }{\sum\limits_{k}{{{W}_{\psi }}(j,k)}}{{\psi }_{j,k}}(x) \\ \end{align}$ | (5) |
其中: f(x)、φj0,k(x)和ψj,k(x)是离散变量x=0,1,2,…,K-1的函数。通常情况下,j0=0,K是2的幂,例如K=2J。式(3) ~(5) 是在x=0,1,2,…,K-1,j=0,1,2,…,J-1和k=0,1,2,…,2J-1上求和。将式(3) 和式(4) 中的系数分别称为近似和细节。
φ(x)是伸缩函数,φj0,k(x)是φ(x)经过变换和伸缩得到的,具体公式如下:
| ${{\varphi }_{j}}_{,k}(x)={{2}^{j/2}}\varphi ({{2}^{j}}x-k)$ | (6) |
ψj,k(x)是小波函数ψ(x)经过伸缩和平移变换得到的,具体公式如下:
| ${{\psi }_{j}}_{,k}(x)={{2}^{j}}^{/2}\psi ({{2}^{j}}x-k)$ | (7) |
把一维离散小波变换重复地应用在矩阵的水平数据和垂直数据上,就实现了二维离散小波变换。
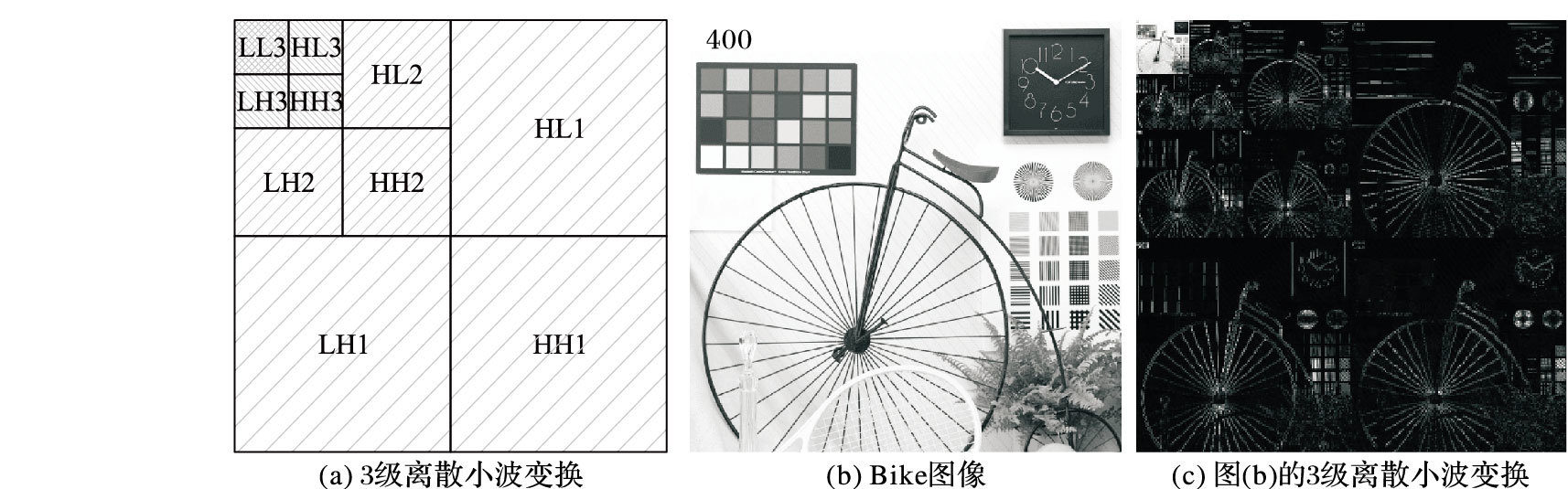
1.5.2 离散小波变换在图像中的应用处在任何一级的小波系数,对其低频信道进行分解就能得到下一级的分解系数。在每一级对图像进行二维离散小波变换,该图像就能被分解成4个子带LL、LH、HL和HH,分别对应图像的低频分量、垂直分量、水平分量和对角分量。图 1中:(a)给出了3级二维离散小波变换;(b)给出了标准测试图像Bike;(c)给出了对图像Bike进行3级离散小波变换的结果。
|
图 1 小波图像变换 Figure 1 Wavelet image transformation |
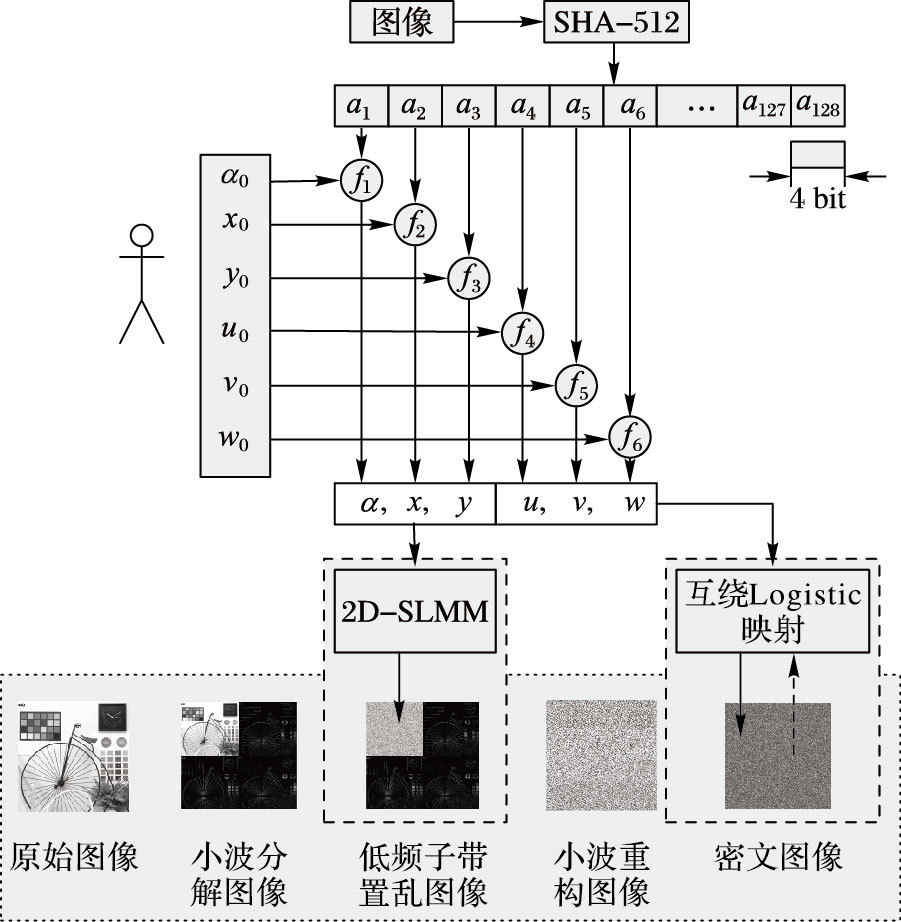
首先,对原始图像执行一级二维离散小波变换,得到四个不重叠的多分辨率系数集:LL1、HL1、LH1和HH1; 接着,使用2D-SLMM混沌动力系统生成混沌序列,并使用该序列置乱LL1,具体置乱算法为混沌魔方变换算法[6]; 此后,完成逆离散小波变换,生成置乱图像; 最后,在空域完成图像替换和扩散操作,其中像素变换采用有限域多项式乘法和异或操作。整体框架见图 2。
|
图 2 本文方案框架图 Figure 2 Framework of the proposed scheme |
步骤1 读取图像X,使用SHA-512算法得到原始图像的哈希值。
h=hash(X(:),′SHA- 512′)
步骤2 依据比特序列,把获取的哈希值分成128组,每组4个比特。随机选取6组,例如:a1,a2,a3,a4,a5,a6。
步骤3 获取用户初始密钥α0,x0,y0,u0,v0,w0。
步骤4 计算两个混沌动力系统的初始变量值。
f1:α=α0+mod(a1/2016,(1-α+))
f2:x=x0+mod(a2/2016,(1-x+))
f3:y=y0+mod(a3/2016,(1-y+))
f4:u=u0+mod(a4/2016,(1-u+))
f5:v=v0+mod(a5/2016,(1-v+))
f6:w=w0+mod(a6/2016,(1-w+))
其中:v0=0.25,w0=0.36。
步骤5 对原始图像进行一级二维离散小波分解,提取低频小波系数。这里小波基可以取Haar、Daubechies、Biorthogonal、Coiflets、Symlets、Morlet、Mexican Hat、Meyer等。
步骤6 使用2D-SLMM混沌动力系统生成混沌序列。
步骤7 使用混沌魔方变换置乱低频子带,具体过程如下:
1) 对混沌矩阵SM×N的每一列排序得到排序矩阵T,其中M代表图像的高度,N代表图像的宽度。
2) 通过下面规则生成置乱索引矩阵I:
T(i,j)=S(k,j),则令I(i,j)=k
3) 把低频子带矩阵L中位置是(Ii,1,1) ,(Ii,2,2) ,(Ii,3,3) ,…,(Ii,N,N)的像素连接成一个循环链表。
4) 把循环链表中的像素向左移动i(i初值为1) 个位置。
5) 重复3)~4)直到i=M,得到被置乱的低频子带矩阵L′。
步骤8 用所有小波系数完成一级逆离散小波重构。
步骤9 对于置乱后的图像进行空域加密,加密的顺序是从第一个字节到最后一个字节。
1) 迭代式(2) 生成3分量向量(u,v,w),接着得出像素值选择变量:
| $op=\text{mod}(\text{fix}((v\times {{2}^{n}}-fix(v\times {{2}^{n}}))\times {{2}^{n+k}}),2)$ | (8) |
2) 如果op=0,使用伽罗瓦域元素乘法加密当前像素:
| $\left\{ \begin{align} & cipher=\text{poly }\!\!\_\!\!\text{ mult}\left( plaintext,key,m\left( x \right) \right) \\ & m\left( x \right)={{x}^{8}}+{{x}^{4}}+{{x}^{3}}+x+1 \\ \end{align} \right.$ |
其中:AB=poly_mult(A,B,MOD_POL)表示在伽罗瓦域GF(28)上执行元素A、B乘法运算;MOD_POL代表度为8的不可约模多项式。
如果op=1,使用异或操作模式加密当前像素:
| $\left\{ \begin{align} & cipher=xor\left( plaintext,key \right) \\ & key=\text{mod}(\text{fix}((u\times {{2}^{m}}-\text{fix}(u\times {{2}^{m}}))\times {{2}^{m}}^{+j}),255)+1 \\ \end{align} \right.$ |
3) 使用式(9) 生成长度为len的二值向量:
| $\left\{ \begin{align} & \mathit{\boldsymbol{V}}=({{b}_{1}},{{b}_{2}},\cdots \cdots ,{{b}_{len}}) \\ & feedback=\text{mod}(\text{fix}((w\times {{2}^{r}}-\text{fix}(w\times {{2}^{r}}))\times {{2}^{r}}^{+s}),{{2}^{len}}) \\ & {{b}_{i}}=\text{bitget}\left( feedback,i \right);i\in \left\{ 1,2,\ldots ,len \right\}; \\ \end{align} \right.$ | (9) |
其中:bitget(A,i)表示提取整数A的第i个比特。
4) 对于当前的密文像素,应用如下的密文反馈模式重加密:
| $\left\{ \begin{align} & {{E}_{i}}=(ciphe{{r}_{i}}\oplus {{b}_{1}}\times E(i-1)\oplus {{b}_{2}}\times \\ & E(i-2)\oplus \cdots \oplus {{b}_{i-1}}\times E(1)),i\le L \\ & {{E}_{i}}=(ciphe{{r}_{i}}\oplus {{b}_{1}}\times E(i-1)\oplus {{b}_{2}}\times \\ & E(i-2)\oplus \cdots \oplus {{b}_{L}}\times E(i-L)),\ italic>L \\ \end{align} \right.$ |
5) 扰动分量u,得到的扰动结果u′作为互绕Logistic映射的输入值。
6) 重复步骤1) ~5) ,直到最后一个像素完成。
步骤10 整个加密过程结束。
2.3 解密过程由于本文的加密方案是对称加密算法,故解密过程和加密过程类似,唯一的区别是算法的执行顺序。当解密图像时,首先完成空域的解密工作,然后执行频域的逆置乱变换,最后得到原始图像。
3 实验结果为了验证本文算法的可行性和有效性,进行了大量的实验。下面以灰度图像Bike和索引图像lily为例,给出原始图像和密文图像的空间直方图。从图 3所示的实验结果可以看出,本文方案具有很好的密文空间分布。

|
图 3 原始图像、密文图像及其直方图 Figure 3 Original image, ciphertext image and their histograms |
在引入小波变换前,本文实现了基于空域的图像加密算法,即直接在空域应用伽罗瓦域乘法和异或相混合的变换方式对像素加密,尽管视觉看不出基于空域密文图像和基于混合域密文图像的区别,但应用像素变化率(Number of Pixel Change Rate,NPCR)和一致均匀变化强度(Unified Average Change Intensity,UACI)对密文图像进行测试,发现NPCR≈99.37%,UACI≈33.23%,和理论值(NPCR≈99.609 4% 和 UACI≈33.463 5%)[7]有一定差距。这一事实表明基于空域的图像加密受到差分攻击的威胁。因此,本文算法引入小波变换是必要的。
NPCR和UACI定义如下:
| $NPCR=\frac{1}{MN}\sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{N}{\left| \text{sign}({{\mathit{\boldsymbol{C}}}_{1}}(i,j)-{{\mathit{\boldsymbol{C}}}_{2}}(i,j)) \right|}}\times 100%$ |
| $UACI=\frac{1}{MN}\sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{N}{\frac{\left| {{\mathit{\boldsymbol{C}}}_{1}}(i,j)-{{\mathit{\boldsymbol{C}}}_{2}}(i,j) \right|}{255}}}\times 100%$ |
其中:C1和C2代表图像矩阵,M、N分别代表图像的高度和宽度。
4.2 离散小波分解级数的讨论依照文献[17]给出的频域图像置乱算法,本文首先对原始图像完成离散小波分解,接着置乱低频子带,然后完成逆离散小波变换,实现图像小波域置乱。图 4给出了在不同小波分解级数情况下的图像置乱结果。可以看出,随着离散小波分解级数的增加,被置乱低频子带系数的数目减少,置乱后获取的图像轮廓信息变得越来越清楚。大量的实验结果表明,采用2级或2级以上离散小波分解的置乱算法,信息泄露问题严重。依据这一理论,文献[17]算法提出采用三级小波分解置乱的算法具有弱安全性。为了避免信息泄露进而提高安全性,本文方案采用一级离散小波分解置乱的算法。

|
图 4 基于不同级数的离散小波分解置乱结果 Figure 4 Scrambling results based on discrete wavelet decomposition with different levels |
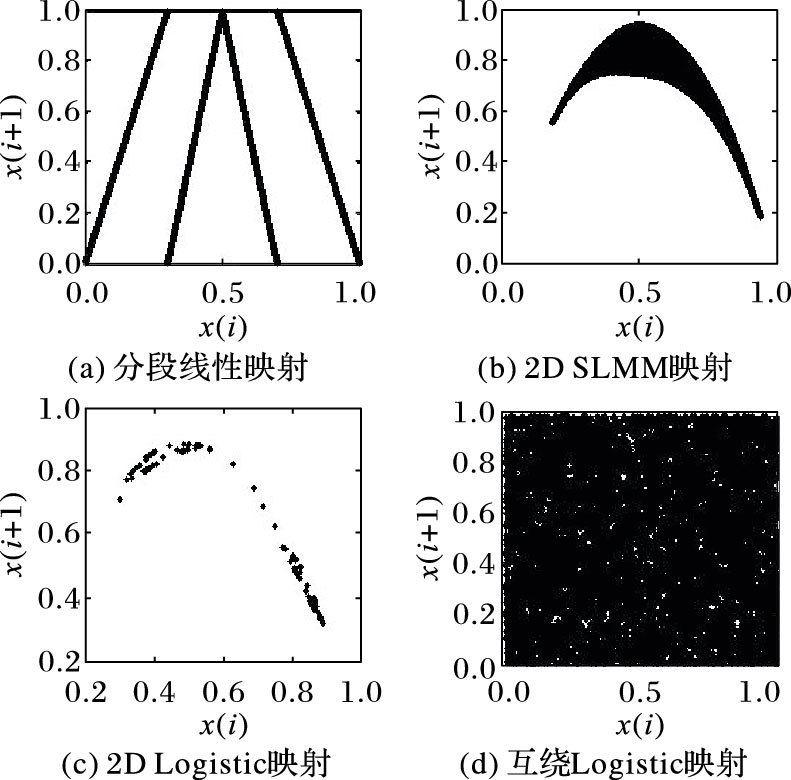
密钥相空间是加密算法安全性的重要组成部分,密钥相空间越大,加密算法越安全。本文算法的密钥相空间包括频域置乱密钥相空间和空域加密密钥相空间。文献[17]算法的频域置乱密钥由一维分段线性混沌映射生成,空域加密密钥由2D Logistic映射生成;本文算法的频域置乱密钥由2D SLMM映射生成,空域加密由互绕Logistic映射生成。这两种方案的频域置乱密钥空间和空域加密密钥空间比较如图 5所示。可以看出,无论是频域置乱密钥相空间还是空域加密密钥相空间,本文算法均优于文献[17]算法。
|
图 5 各映射函数相空间 Figure 5 Phase space of each mapping function |
从密钥相空间具体量化指标来看,假设计算机计算精度为10-14,则文献[17]算法的相空间为10112,本文算法的相空间为10154。因此,本文算法的相空间优于文献[17]算法。
4.4 像素零的处理在本文提出的加密算法中利用伽罗瓦域上乘法加密像素,其加密强度高于模加和异或、低于公钥加密算法。然而,运用伽罗瓦域上乘法加密像素的主要缺陷是不能处理像素零。因此,当加密过程跳转到伽罗瓦域元素乘法模式并且加密对象又是零像素时,算法规定加密对象保持不变,这个零元像素由随后的反馈加密决定。总之,原始图像的像素零由置乱和反馈加密决定。
4.5 重构攻击分析随着混沌信号估计技术的发展,当少量混沌序列信息被提取时,对应的混沌轨道有可能被估计,对应的参数或初值有可能被预测。这种技术被称为相空间重构,是以Taken延迟嵌入理论为基础的。使用混沌序列生成加密密钥的加密算法有可能受到相空间攻击的威胁。为了重构相空间,获取同一动力系统的观测状态序列是前提。但是,对于本文方案,攻击者观测的序列已经被密文扰动。依据混沌序列的敏感性,扰动序列和混沌原始序列完全不同。因此,相空间重构攻击不起作用。文献[17-18]都没有对混沌映射生成的序列进行扰动,存在重构攻击的风险。
4.6 差分攻击分析攻击者经常使用加密算法加密原始图像和其修改后的图像,然后比较两个加密图像以找出原始图像和加密图像的相关性。这种攻击称为差分攻击[25]。具有理想扩散属性的加密算法能够抵御差分攻击。指标NPCR和UACI能够反映加密系统抵御差分攻击的能力。
以Bike、 Lily、 Lena和Baboon图像为例,对于每一图像随机地选取一位置并轻微地修改对应位置的值,计算它们的NPCR和UACI,并重复100次后计算平均值,结果如表 1所示。可以看出,NPCR和UACI的测试值非常接近理论值。这些实验可以证明建议算法能够有效抵御差分攻击。依据文献[17]给出的实验结果NPCR≈99.48%,UACI≈33.28%,表明该方案和理论值有一定差距。文献[18]给出空域加密2轮后的结果NPCR>99.6%,UACI>33.4%,接近理论值。由此可见本文算法在抗差分攻击方面优于文献[17]算法。
| 表 1 明文敏感性测试结果 Table 1 Sensitivity test results of plaintext |
除了安全方面,加密系统的运行速度是评估图像加密算法的另一重要因素。从算法时间复杂度来看,本文方案的时间复杂度为O(P)+O(Q)+O(R),文献[17]算法的时间复杂度也为O(P)+O(Q)+O(R),文献[18]的时间复杂度为O(P)+O(Q)+O(2R)。其中:O(P)、O(Q)、O(R)分别代表小波分解时间复杂度、频域置乱时间复杂度以及空域加密复杂度,O(2R)代表空域进行2轮加密时间复杂度。
下面以Lily和Bike图像(大小为512×512) 为例分析算法的实际运行时间,其中本文算法由Matlab R2012实现。算法最初加密512×512的图像耗时为4.6 s,耗时太多。利用Matlab探测器观察程序每一部分的耗时情况发现,伽罗瓦域上元素乘法耗时2.4 s,占据整个运行时间的52%。为了提高运行效率,提前计算伽罗瓦域GF(256) 上所有可能的元素乘法,将原来的元素乘法用查表法代替,这样能使加密速度得到显著提升,加密一幅图片大约需要2.34 s。考虑到本文算法和文献[17]算法具有相同的时间复杂度,而文献[17]算法加密同样大小的图像时间约为708~730 ms,故进一步优化了频域置乱算法并且对数组变量进行了存储空间预分配,这样加密一幅图像平均需要720 ms,实现了时间复杂度和实际运行时间的统一。采用文献[18]加密同样大小图像大约需要950 ms。
从时间复杂度和实际运行时间来看,本文方案加密速度具有可行性。
4.8 和现有加密算法其他方面的比较文献[17-18]算法和本文算法都是基于混合域的图像加密算法,即置乱在小波域,替换和扩散在空域。在明文敏感性保证方面,文献[17]算法和本文算法都采用了哈希函数来保证敏感性;而文献[18]是通过传统的空域多轮加密方式来保证,这种通过时间来换取敏感性的算法导致其加密效率低于文献[17]算法和本文算法。在像素变换加密方面,文献[17]只采用了简单异或方式来实现;而文献[18]采用了异或组合移位等多种基本操作集合,然而通过这种简单操作实现的加密算法易于破解[22-23];本文则采用了基于伽罗瓦域元素乘法和异或混合的像素变换加密方式,提高了加密算法的安全性。
5 结语在设计图像加密算法的过程中,安全为第一驱动力,速度位居其次。基于这一理念,本文分析了基于混沌理论的混合域图像加密算法的代表性文献[17],针对其加密强度弱的缺点,设计了一个新的混合域加密算法。首先,执行图像的一级小波分解,接着在小波域使用二维置乱变换——混沌魔方变换重排了原始图像的低频系数;然后完成逆离散小波变换;此后,空域的像素变换被连续应用到置乱图像,使得最终图像无法理解。值得一提的是,伽罗瓦域上的多项式乘法被首次应用完成像素变换,这一做法极大地增强了加密算法的安全性。另外,采用密文反馈和扰动技术实现了一次性密钥。利用模拟实验比较了相关算法的性能,结果表明本文算法具有高安全性。
| [1] | KUMAR M, IQBAL A, KUMAR P. A new RGB image encryption algorithm based on DNA encoding and elliptic curve Diffie-Hellman cryptography[J]. Signal Processing, 2016, 125 : 187-202. doi: 10.1016/j.sigpro.2016.01.017 |
| [2] | YANG Y-G, TIAN J, LEI H, et al. Novel quantum image encryption using one-dimensional quantum cellular automata[J]. Information Sciences, 2016, 345 : 257-270. doi: 10.1016/j.ins.2016.01.078 |
| [3] | 葛滨, 鲁华祥, 陈旭, 等. 基于超混沌的快速图像加密算法[J]. 系统工程与电子技术, 2016, 38 (3) : 699-705. ( GE B, LU H X, CHEN X, et al. Fast image encryption algorithm based on hyper-chaos[J]. System Engineering and Electronics, 2016, 38 (3) : 699-705. ) |
| [4] | WADI S M, ZAINAL N. Rapid encryption method based on aes algorithm for grey scale HD image encryption[J]. Procedia Technology, 2013, 11 : 51-56. doi: 10.1016/j.protcy.2013.12.161 |
| [5] | SHATHEESH SAM I, DEVARAJ P, BHUVANESWARAN R S. An intertwining chaotic maps based image encryption scheme[J]. Nonlinear Dynamics, 2012, 69 (4) : 1995-2007. doi: 10.1007/s11071-012-0402-6 |
| [6] | HUA Z, ZHOU Y, PUN C-M, et al. 2D Sine Logistic modulation map for image encryption[J]. Information Sciences, 2015, 297 : 80-94. doi: 10.1016/j.ins.2014.11.018 |
| [7] | ZHANG Y. The image encryption algorithm with plaintext-related shuffling[J]. IETE Technical Review, 2016, 33 (3) : 310-322. doi: 10.1080/02564602.2015.1087350 |
| [8] | CAO G, ZHANG X, LIU Y. Image encryption with variable length key[J]. IETE Technical Review, 2016, 33 (3) : 297-309. doi: 10.1080/02564602.2015.1088412 |
| [9] | SHATHEESH SAM I, DEVARAJ P, BHUVANESWARAN R S. An intertwining chaotic maps based image encryption scheme[J]. Nonlinear Dynamics, 2012, 69 (4) : 1995-2007. doi: 10.1007/s11071-012-0402-6 |
| [10] | FRIDRICH J. Symmetric ciphers based on two-dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8 (6) : 1259-1284. doi: 10.1142/S021812749800098X |
| [11] | LIMA J B, MADEIRO F, SALESC F J R. Encryption of medical images based on the cosine number transform[J]. Signal Processing:Image Communication, 2015, 35 : 1-8. doi: 10.1016/j.image.2015.03.005 |
| [12] | TEDMORI S, AL-NAJDAWIB N. Image cryptographic algorithm based on the Haar wavelet transform[J]. Information Sciences, 2014, 269 : 21-34. doi: 10.1016/j.ins.2014.02.004 |
| [13] | TANEJA N, RAMAN B, GUPTA I. Selective image encryption in fractional wavelet domain[J]. AEU-International Journal of Electronics and Communications, 2011, 65 (4) : 338-344. doi: 10.1016/j.aeue.2010.04.011 |
| [14] | HENNELLY B, SHERIDAN J T. Fractional Fourier transform-based image encryption:phase retrieval algorithm[J]. Optics Communications, 2003, 226 (1/2/3/4/5/6) : 61-80. |
| [15] | PHILIPPE R, JAVIDI B. Optical image encryption based on input plane and Fourier plane random encoding[J]. Optics Letters, 1995, 20 (7) : 767-769. doi: 10.1364/OL.20.000767 |
| [16] | LIU Z, LI S, LIU W, et al. Image encryption algorithm by using fractional Fourier transform and pixel scrambling operation based on double random phase encoding[J]. Optics and Lasers in Engineering, 2013, 51 (1) : 8-14. doi: 10.1016/j.optlaseng.2012.08.004 |
| [17] | ZHANG X, ZHU G, MA S. Remote-sensing image encryption in hybrid domains[J]. Optics Communications, 2012, 285 (7) : 1736-1743. doi: 10.1016/j.optcom.2011.12.023 |
| [18] | ABD EL-LATIF A A, NIU X, AMIN M. A new image cipher in time and frequency domains[J]. Optics Communications, 2012, 285 (21/22) : 4241-4251. |
| [19] | ARROYO D, RHOUMA R, ALVAREZ G, et al. On the security of a new image encryption scheme based on chaotic map lattices[J]. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2008, 18 (3) : 033112. doi: 10.1063/1.2959102 |
| [20] | LING C, WU X, SUN S. A general efficient method for chaotic signal estimation[J]. IEEE Transactions on Signal Processing, 1999, 47 (5) : 1424-1428. doi: 10.1109/78.757236 |
| [21] | LI C, CHEN G. On the security of a class of image encryption schemes[C]//ISCAS 2008:Proceedings of the 2008 IEEE International Symposium on Circuits and Systems. Piscataway, NJ:IEEE, 2008:3290-3293. |
| [22] | LI C, LIU Y, ZHANG L Y, et al. Breaking a chaotic image encryption algorithm based on modulo addition and XOR operation[J]. International Journal of Bifurcation & Chaos, 2013, 23 (4) : 1350075. |
| [23] | WU X, HU H, ZHANG B. Parameter estimation only from the symbolic sequences generated by chaos system[J]. Chaos, Solitons & Fractals, 2004, 22 (2) : 359-366. |
| [24] | RGONZALEZ R C, WOODS R E. Digital Image Processing[M]. Upper Saddle River, NJ: Prentlce-Hall, 2012 : 510 -512. |
| [25] | RHOUMA R, SOUMAYA M. OCML-based colour image encryption[J]. Chaos, Solitons & Fractals, 2009, 40 (1) : 309-318. |




