Delaunay三角剖分在图形学、地理学以及有限元分析等领域是一项极为重要的预处理技术。随着计算机技术的发展以及分析对象的复杂性,Delaunay三角剖分在这些领域扮演着重要角色。例如,在有限元分析中,需要把研究的区域分解成三角形单位元。如果剖分的三角形角度过小,那么有限元算法的收敛性得不到保证。因为Delaunay三角剖分可以最大化最小角,所以Delaunay三角剖分是一种有效的剖分方法。
目前,平面上的Delaunay三角剖分的研究已经相当成熟。平面上的Delaunay三角剖分分为点集Delaunay三角剖分和约束Delaunay三角剖分。对于平面点集Delaunay三角剖分来说,Lee等[1]给出了点集Delaunay三角剖分的几何性质和算法。Dwyer[2]利用分治合并算法构建了点集Delaunay三角剖分。近年来,对于点集Delaunay三角剖分的研究都是不断降低时间复杂度,插入点混合定位算法[3]有效降低算法的时间复杂度。对于平面约束Delaunay三角剖分来说,Chew[4]提出了分治合并算法,Lee等[5]对平面直线图形作约束Delaunay三角剖分。近几年,关于平面约束Delaunay三角剖分的研究也都是不断降低复杂度,如带断层约束的Delaunay三角剖分混合算法[6],它在生成网格质量和时间效率上都优于传统算法。随着计算机技术的发展,约束Delaunay三角剖分已经不能满足生产需求。在有限元分析中,网格的质量对有限元方程的收敛性有着直接的影响。Ruppert[7]通过添加“Steiner”点提出Delaunay Refinement算法以及Shewchuk[8]提出的Delaunay Refinement算法增大了输出三角形的最小角角度,这些网格都适用于有限元方程。但是Ruppert's Refinement算法复杂度的证明由Barbic等[9]完成。Rand[10]提出的“Off-Centers”不仅提高输出三角形的质量,还添加更少的输出点。
近年来,出现了非欧空间的Delaunay三角剖分,如Caroli等[11]给出了球面点集Delaunay三角剖分和Zeng等[12]提出的双曲曲面Delaunay Refinement三角剖分。在计算Ricci Flow方程时,一旦出现某个退化的球面三角形,就有可能出现不收敛的情况,文献[13-14]研究就需要高质量的球面三角形。因此,必须提高球面三角形的质量。本文通过添加Delaunay劣弧中点以及球面三角形外接测地圆圆心,有效地提高整体球面三角形的质量,避免狭小角的出现,有效解决Ricci Flow方程不收敛的问题。
1 球面凸类图形Delaunay三角剖分再分算法首先,给出几个相关概念。
定义1 球面上两点之间劣弧的长度, 称之为球面上两点之间的距离, 简称距离。
定义2 球面n边形A1A2…An总在它的每一边所在大圆的半个球面内, 那么称这个球面多边形为球面凸n边形。
定义3 球面凸n边形以及包含在球面凸n边形内的点和劣弧称为球面凸类图形。
因为不同半径的球面之间可以建立一一映射,所以不妨在单位球面上对输入的球面凸类图形进行Delaunay三角剖分再分,如果没有特殊说明,下文中的球面指的是单位球面。
为了方便,假设球面凸类图形中球面凸n边形两条相交劣弧夹角角度至少是90°,这个限制根据文献[7]中的“Corner-Lopping”可以解除,具体不再赘述;同时,记球面凸类图形为X。另外本文中提到的角指的是球面角。
球面凸类图形Delaunay三角剖分再分算法是在球面点集Delaunay三角剖分算法基础上生成的,球面点集Delaunay三角剖分(Sphere Delaunay Triangulation (V))简记为SDT(V)。球面点集Delaunay三角剖分指的是给定球面上一系列点,由球面点集Delaunay三角剖分算法产生的所有球面三角形最短边对应的外接球面小圆圆心角达到最大,也就是最大化最小圆心角。如果球面上不存在四点共圆,那么这个SDT(V)是唯一的。如果存在四点共圆,两条对角线任取一条不影响最小圆心角的大小,不妨取对角线最短的作为边。具体的算法实现见参考文献[11]。为了方便下文的分析,本文只需要对球面凸类图形内部进行Delaunay三角剖分再分,故球面凸类图形外的球面三角形全部删除。
把球面凸类图形中的劣弧以及剖分产生的劣弧叫作Delaunay劣弧,用集合G表示。球面上任意一条劣弧AB记为AB。为了方便,也可用AB表示球面上A和B两点之间的距离,那么球面上AB的取值范围为(0, π]。同时,把球面凸类图形中的点以及剖分添加的点叫作顶点,用集合V表示。球面上任意一个点叫作点。对于这个算法,初始时,V就是所有输入的顶点,G就是所有的输入劣弧。
生成球面点集Delaunay三角剖分之后,利用本文算法继续剖分,添加点的原因有两个:保证G中的Delaunay劣弧是点集Delaunay三角剖分产生的测地线;整体提高球面三角形最短边外接球面小圆圆心角。
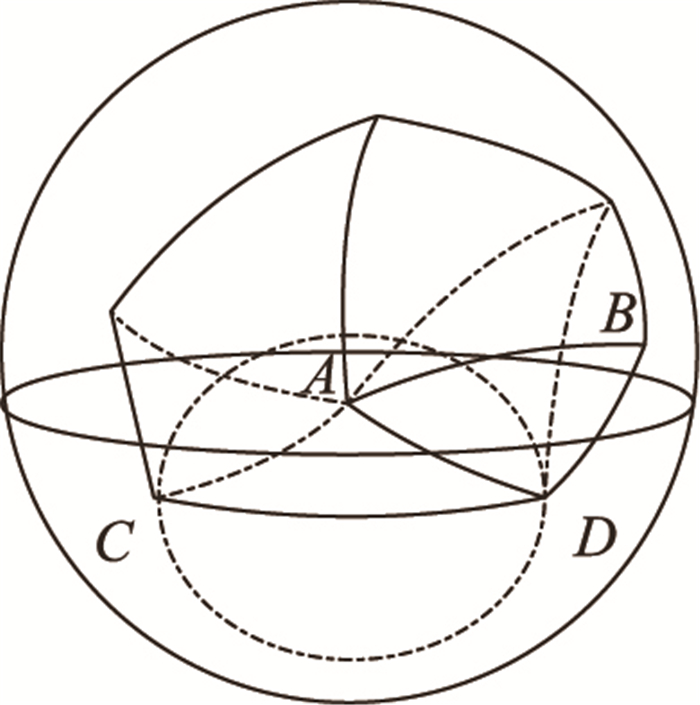
对Delaunay劣弧g来说,以g为测地直径的球面小圆称为g的测地直径圆。如果有一个顶点A在g的测地直径圆内,称顶点A“侵占”Delaunay劣弧g。如图 1所示,输入的球面凸类图形是图中的实Delaunay劣弧,球面点集Delaunay三角剖分是图中除Delaunay劣弧AB外,其他实Delaunay劣弧和虚劣弧组成的图形。对于球面凸类图形来说,这不是它的Delaunay三角剖分,因为AB不是点集Delaunay三角剖分中的测地线且顶点A“侵占”Delaunay劣弧CD。
|
图 1 非法球面Delaunay三角剖分 Figure 1 Delaunay triangulation of illegal sphere |
本文算法的核心操作有两个:第一,如果某条Delaunay劣弧被“侵占”,通过添加Delaunay劣弧中点分割Delaunay劣弧;第二,如果存在“瘦”球面三角形,通过添加球面三角形外接球面小圆圆心分解球面三角形,“瘦”球面三角形是球面三角形外接球面小圆中,球面三角形最短边对应的圆心角的角度小于φ(φ是预先给定的值)的球面三角形。
下面给出球面凸类图形Delaunay三角剖分再分算法:
输入 球面凸类图形X和参数φ。
BEGIN
初始化 计算初始球面点集Delaunay三角剖分SDT(V)
while Delaunay劣弧g被“侵占”:
SpliltGeo(Delaunay劣弧g)
if“瘦”球面三角形t的外接球面小圆圆心P “侵占”Delaunay劣弧g1, g2, …, gk
for i=1 to k:
SplitGeo(Delaunay劣弧gi)
else SplitStri (球面三角形t)
end if
until没有Delaunay劣弧被“侵占”和没有球面三角形最短边所对应的圆心角<φ
END
子算法SplitStri(球面三角形t)。
输入 球面三角形t。
BEGIN
添加球面三角形t的外接球面小圆圆心到V中,更新SDT(V)
END
子算法SplitGeo(Delaunay劣弧g)。
输入 Delaunay劣弧g。
BEGIN
添加Delaunay劣弧g的中点到V中,更新SDT(V),将g从G中移除,将g分成的两个子段g1和g2添加到G中
END
2 算法收敛性分析在本章证明本文算法在执行有限的步骤之后是可以终止的,这与输入球面凸类图形的局部特征尺度有关,给出局部特征尺度的概念。
定义4 给定一个球面凸类图形X,以球面上任意一点P为圆心的与X中两个和P不相关的顶点或Delaunay劣弧相交的最小球面小圆的测地半径叫作点P的局部特征尺度,记为lfs(P)。
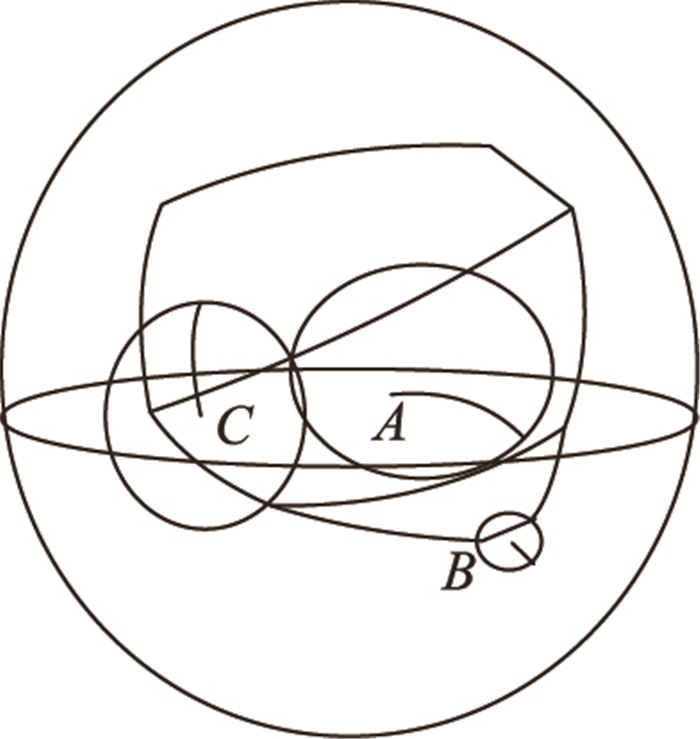
在球面上,根据定义1知,lfs(P)的取值范围为(0, π)。图 2是对这个定义的直观解释,lfs(A)、lfs(B)和lfs(C)分别对应图 2中三个球面小圆的测地半径,其中lfs(C)有一部分顶点或Delaunay劣弧相交。对于给定的输入球面凸类图形X,lfs(X)是连续函数且满足下列引理1。
|
图 2 局部特征尺度 Figure 2 Local feature scale |
引理1 局部特征尺度是Lipschitz函数,即任意给定一个球面凸类图形,在球面上任取两个点P和Q,有:
| $ lfs(Q) \le lfs(P) + PQ $ |
其中PQ是球面上两点P和Q的距离。
证明 根据lfs()的定义,lfs(P)是以点P为圆心的与球面凸类图形中两个和P不相关的顶点或Delaunay劣弧相交的最小球面小圆的测地半径,记这个球面小圆为D1。
1) 若lfs(P)+PQ≥π,因为lfs()<π,显然成立。
2) 若lfs(P)+PQ<π,现在以点Q为圆心,r=lfs(P)+PQ为测地半径的球面小圆记为D2,那么D1包含在D2中,因此:
| $ lfs(Q) \le r $ |
故得到:
| $ lfs(Q) \le r = lfs(P) + PQ $ |
每当一个点添加之后,它不改变lfs()的性质,lfs()只和输入的球面凸类图形有关,下面的引理2说明顶点的密度完全是由lfs()决定。
引理2 1) 初始时,对于每个输入的顶点P,P到它最近的顶点的距离至少是lfs(P)。
2) 当点P是球面“瘦”球面三角形的外接球面小圆圆心时,点P到它最近顶点的距离至少是lfs(P)/CT(点P属于这个三角剖分中的顶点或者是“侵占”某条Delaunay劣弧)。
3) 当顶点P是某条Delaunay劣弧的中点时,点P到它最近的顶点的距离至少为lfs(P)/CG。
证明 当顶点P是输入的点时,根据lfs()的定义,顶点P到它最近的顶点的距离至少是lfs(P)。对于后来加进去的点,假设这个引理对之前所有的顶点都成立。
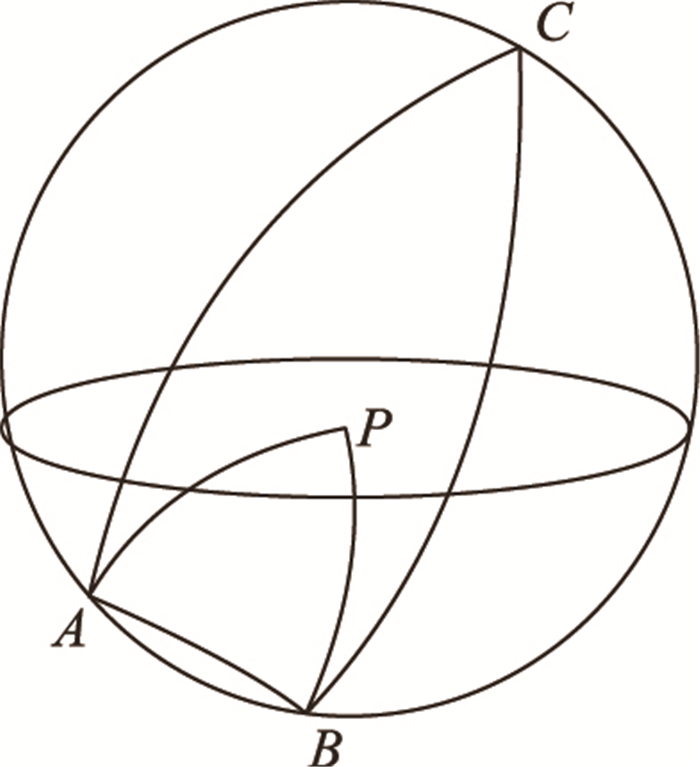
1) 当点P是球面“瘦”三角形t的外接球面小圆圆心时,那么点P到球面“瘦”三角形t的顶点最近。设点P到球面“瘦”三角形t的顶点A、顶点B和顶点C的距离等于r1,那么r1的取值范围为(0, π/2)。如图 3所示,不妨假设弧AB是球面△ABC的最短边,那么弧AB所对应的圆心角最小,设为ψ。
|
图 3 球面三角形及其圆心角 Figure 3 Spherical triangle and its central angle |
不失一般性,首先考虑点A是在点B之后加进去的或者两者都是输入的顶点。当点A是输入的顶点时,则lfs(A)≤AB;当点A是球面三角形外接球面小圆圆心时,设这个球面小圆的测地半径为rA,根据这个引理有lfs(A)≤CTrA≤CTAB;当点A是某条Delaunay劣弧的中点时,在A点利用这个引理有lfs(A)≤CGAB。
假设给定条件CG≥CT≥1,则上面几种情况综合起来为:
| $ lfs(A) \le {C_G}AB $ |
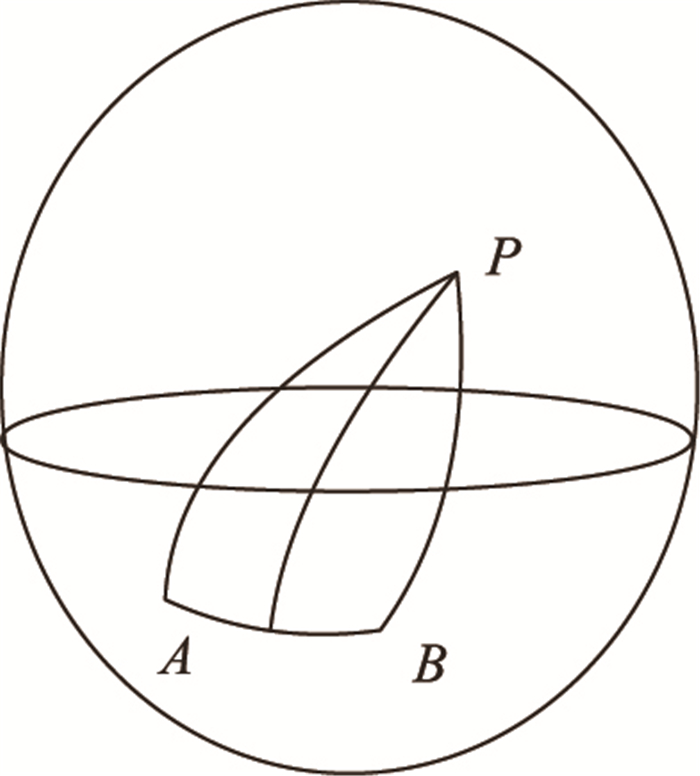
如图 4所示,先把球面△PAB提出来,再由点P作AB的垂线,根据球面正弦定理有:
| $ \frac{{\sin {r_1}}}{{\sin \left( {{\rm{ \mathsf{ π} }} /2} \right)}} = \frac{{\sin \left( {\left( {AB} \right)/2} \right)}}{{\sin \left( {\psi /2} \right)}} $ |
|
图 4 球面三角形及其垂线 Figure 4 Spherical triangle and its vertical |
由此得到:
| $ AB = 2\arcsin (\sin \left( {\psi /2} \right) \cdot \sin {r_1}) $ |
令ρ(ψ, r1)=(AB)/(2r1),因为:
| $ lfs(P) \le lfs(A) + {r_1} $ |
则ρ(ψ, r1)在r1∈(0, π/2)上的最大值的上确界为sin(ψ/2),得:
| $ {r_1} \ge \frac{{lfs(P)}}{{2\sin \left( {\psi /2} \right){C_G} + 1}} $ |
这里只需要取CT≥2sin(ψ/2)CG+1。
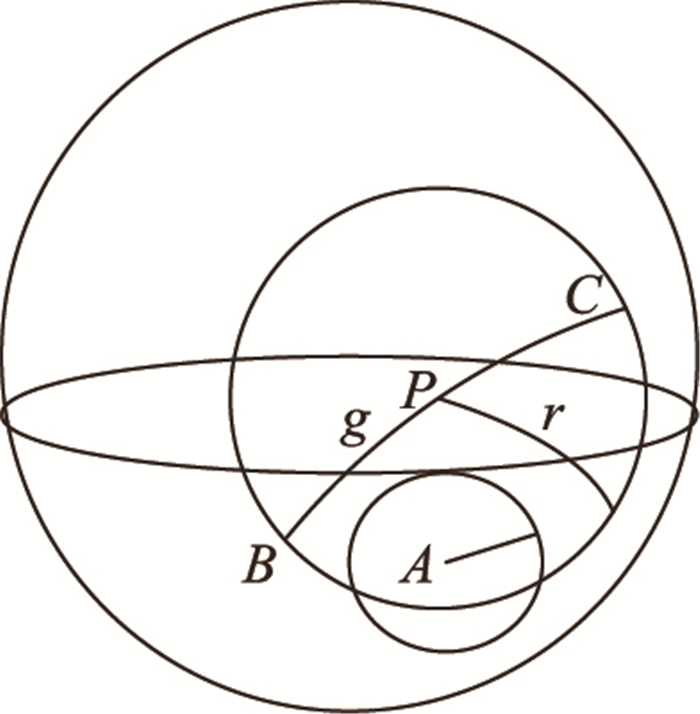
2) 如图 5所示,当顶点P是Delaunay劣弧g的中点时,如果存在顶点A或某个球面“瘦”三角形外接球面小圆圆心A在以g为测地直径的球面小圆内时,Delaunay劣弧g需要添加中点并假设这个球面小圆的测地半径为r2,易知,r2的取值范围为(0, π/2)。
|
图 5 点A “侵占”劣弧BC Figure 5 Vertex A "encroaches upon" minor arc BC |
a) 点A位于Delaunay劣弧h上并且和Delaunay劣弧g不相交,之前假设所有的输入球面凸类图形的角度至少是90°,所以必然存在两个不相交的Delaunay劣弧,一个包含点P,另一个包含点A,使得它们的距离比r2小。因此,得到:
| $ lfs(P) \le {r_2} $ |
根据CG≥1知,这种情况是成立的。
b) 点A是球面“瘦”三角形外接球面小圆圆心,但是这个点在以Delaunay劣弧g为测地直径的球面小圆内,所以这个点是不存在于三角剖分内。那么存在一个以点A为圆心,测地半径为rA的球面小圆CA使得圆内没有其他点,在A点应用这个引理得到:
| $ {r_A} \ge lfs(A)/{C_T} $ |
同时,点B和点C在CA之外,故当rA最大时有:
| $ \cos {r_A} = \cos {r_2} \times \cos {r_2} $ |
令ρ(r2)=rA/r2,根据引理1有:
| $ lfs(P) \le lfs(A) + {r_2} $ |
ρ(r2)在(0, π/2)上的最大值的上确界为
| $ {r_2} \ge lfs(P)/\left( {\sqrt 2 {C_T} + 1} \right) $ |
这里只需取CG≥2CT+1。
根据上面的分析,得到如下不等式:
| $ \left\{ \begin{array}{l} {C_G} \ge {C_T} \ge 1\\ {C_T} \ge 2\sin \left( {\psi /2} \right){C_G} + 1\\ {C_G} \ge \sqrt 2 {C_T} + 1 \end{array} \right. $ |
通过解这个方程组,得到:
| $ \psi \le 2\arcsin \left( {\sqrt 2 /4} \right) \approx {41.4^ \circ } $ |
所以ψ的一个上界为φ=41.4°。
引理2表明当点P加进去之后,没有其他顶点在以P为圆心、lfs(P)/CG为测地半径的球面小圆内。下面的这个定理表明当点加进去之后,顶点P到其他顶点的距离存在下界。
定理1 给定输出的球面凸类图形的Delaunay三角剖分再分,对于任意一个顶点P,顶点P到它最近的顶点的距离至少是lfs(P)/(CG+1)。
证明 引理2解决了除P在Q之后加入的情况,利用这个引理2对Q进行处理,得到:
| $ PQ \ge lfs(Q)/{C_G} $ |
结合引理1得到:
| $ PQ \ge lfs(P)/\left( {{C_G} + 1} \right) $ |
有了上面的定理之后, 就能证明输出顶点存在上界。
定理2 Delaunay三角剖分再分输出球面三角网格中,顶点的数量至多是:
| $ {C_1}\int_B {\frac{1}{{lf{s^2}(x)}}} {\rm{d}}x $ |
其中:B是球面凸类图形的内部;C1是具体的常数。
证明 在生成的球面网格中,根据定理1得到每个以顶点P为圆心、以lfs(P)/(CG+1)为测地半径的球面小圆内没有其他顶点。现在以顶点P为圆心,以rP=lfs(P)/[2(CG+1)]为测地半径作球面小圆,记为DP。易知,这样构造的测地圆是不可能相交的。再根据球面凸类图形的假设知,每个DP至少有1/4在球面凸类图形内,可以得到
| $ \int_B {\frac{1}{{lf{s^2}(x)}}{\rm{d}}x \ge \frac{1}{4}} \sum\limits_{P \in V} {\int_{{D_P}} {\frac{1}{{lf{s^2}(x)}}} } {\rm{d}}x $ |
根据引理1,在DP中,lfs()的最大值是lfs(P)+rP,设DP的面积为SDP,故:
| $ \int_{{D_P}} {\frac{1}{{lf{s^2}(x)}}} {\rm{d}}x \ge \frac{{{S_{{D_P}}}}}{{{{(lfs(P) + {r_p})}^2}}} $ |
下面对rP分情况讨论:
1) 当rP≤π/2时,因为SDP=4πsin2(rP/2),所以:
| $ \int_{{D_P}} {\frac{1}{{lf{s^2}(x)}}} {\rm{d}}x \ge \frac{8}{{{{(2{C_G} + 3)}^2}{\rm{ \mathsf{ π} }}}} $ |
综合起来得:
| $ \int_B {\frac{1}{{lf{s^2}(x)}}{\rm{d}}x \ge \frac{2}{{{{(2{C_G} + 3)}^2}{\rm{ \mathsf{ π} }}}}} \sum\limits_{P \in V} 1 $ |
因此,只需取
2) 当π/2<rP≤π时,易知SDP=4π-4π sin2((π-rP)/2),同理得:
| $ \int_B {\frac{1}{{lf{s^2}(x)}}} {\rm{d}}x \ge \frac{1}{{{{(2{C_G} + 3)}^2}{\rm{ \mathsf{ π} }}}}\sum\limits_{P \in V} 1 $ |
因此,只需取C1≥(2CG+3)2π即可。
根据以上两种情况知,只需取C1≥(2CG+3)2π。
由上面的分析知,当输入的参数φ≤41°时,本文算法在执行过程中添加的点是有限的,也就是本文算法是收敛的。
3 算法实现及分析球面凸类图形的Delaunay三角剖分再分算法比欧氏空间的Delaunay Refinement Algorithm复杂。Delaunay Refinement Algorithm收敛条件由剖分的三角形最小角限定,本文算法收敛条件是由剖分三角形最短边对应的球面圆心角限定。这是因为球面三角形内角和不是固定常数,导致无法通过球面三角形最小角限定收敛条件。在具体算法实现过程中,球面凸类图形Delaunay三角剖分再分算法比Delaunay Refinement Algorithm更复杂。Delaunay Refinement Algorithm可以由Matlab直接实现并且可视化,但是球面凸类图形Delaunay三角剖分再分算法只能通过程序语言输出边和点的数据,再由其他绘图软件可视化。
本文算法的核心操作和平面的情况是相同的,具体的证明过程见参考文献[9], 所以本文算法的时间复杂度和平面情况相同,都是O(n2)。本文算法的程序实现如图 6所示。

|
图 6 程序实现图(最小圆心角为41.4°) Figure 6 Program implementation diagram (minimum central angle is 41.4°) |
本文算法还可以适当提高最小圆心角的角度,可以在本文算法中插入一个限制球面三角形大小的语句,不妨以球面三角形外接测地圆半径为限制。这种方法可以在球面上作近似均匀剖分,生成尽量同样大小的三角形,并且可以加密剖分,满足许多应用的要求。
4 结语近年来,有关Delaunay三角剖分研究重点仍然是在欧氏空间进行。对于非欧空间的Delaunay三角剖分研究得还不够深入。在求解Ricci Flow方程时,Ricci Flow的收敛性是和剖分的三角形相关的,一旦出现某个角度过小的三角形,Ricci Flow就有可能出现不收敛情况。本文中的三角网格通过提高最短边对应的圆心角提高三角形最小角角度,有效解决不收敛的问题。本文算法中添加的是球面三角形外接测地圆的圆心,下一步可以研究添加“Off-center Steiner Vertices”,或许这种方法输出的点更少,且可以突破本文收敛条件41.4°的限制,提高到更大的角度。
| [1] | LEE D T, SCHACHTER B J. Two algorithms for constructing Delaunay triangulations[J]. International Journal of Computer and Information Sciences, 1980, 9(3): 219-242. DOI:10.1007/BF00977785 |
| [2] | DWYER R A. A faster divide-and-conquer algorithm for constructing Delaunay triangulations[J]. Algorithmica, 1987, 2(1/2/3/4): 137-151. |
| [3] | 高莉. 改进的Deluanay三角剖分算法研究[D]. 兰州: 兰州交通大学, 2015: 30-33. (GAO L. An improved Deluanay triangulation algorithm[D]. Lanzhou:Lanzhou Jiaotong University, 2015:30-33.) http://cdmd.cnki.com.cn/Article/CDMD-10732-1015449171.htm |
| [4] | CHEW L P. Constrained Delaunay triangulation[J]. Algorithmica, 1989, 4(1/2/3/4): 97-108. |
| [5] | LEE D T, LIN A K. Generalized Delaunay triangulation for planar graphs[J]. Discrete & Computational Geometry, 1986, 1(3): 201-217. |
| [6] | 张群会, 解子毅. 带断层约束的Delaunay三角剖分混合算法[J]. 西安科技大学学报, 2014, 34(1): 52-56. (ZHANG Q H, XIE Z Y. Mixed algorithm of Delaunay triangular subdivision with fault constraint[J]. Journal of Xi'an University of Science and Technology, 2014, 34(1): 52-56.) |
| [7] | RUPPERT J. A Delaunay refinement algorithm for quality 2-dimensional mesh generation[J]. Journal of Algorithms, 1995, 18(3): 548-585. DOI:10.1006/jagm.1995.1021 |
| [8] | SHEWCHUK J R. Delaunay refinement algorithms for triangular mesh generation[J]. Computational Geometry, 2002, 22(1/2/3): 21-74. |
| [9] | BARBIC J, MILLER G. A quadratic running time example for ruppert's refinement algorithm[EB/OL].[2017-04-16]. http://www-bcf.usc.edu/~jbarbic/BarbicMiller-RupperQuadraticExampleTechReport.pdf. |
| [10] | RAND A. Where and how Chew's second Delaunay refinement algorithm works[C/OL]//Proceedings of the 201323rd Annual Canadian Conference on Computational Geometry, [2017-04-16]. http://www.w.cccg.ca/proceedings/2011/papers/paper91.pdf. |
| [11] | CAROLI M, DE CASTRO P M M, LORIOT S, et al. Robust and efficient Delaunay triangulations of points on or close to a sphere[C]//Proceedings of the 20109th International Conference on Experimental Algorithms. Berlin:Springer, 2010:462-473. |
| [12] | ZENG W, SHI R, GU X F. Global surface remeshing using symmetric Delaunay triangulation in uniformization spaces[C]//Proceedings of the 2011 Eighth International Symposium on Voronoi Diagrams in Science and Engineering. Piscataway, NJ:IEEE, 2011:160-169. |
| [13] | GU X F, GUO R, LUO F, et al. A discrete uniformization theorem for polyhedral surfaces Ⅱ[EB/OL].[2017-04-16]. http://math.oregonstate.edu/~guoren/docs/u10-10.pdf. |
| [14] | GU X F, GUO R, LUO F, et al. A discrete uniformization theorem for polyhedral surfaces Ⅰ[EB/OL].[2017-04-16]. https://arxiv.org/pdf/1401.4594.pdf. |
| [15] | PREPARATA F P, SHAMOS M I. Computational Geometry-an Introduction[M]. New York: Springer, 1985: 241-276. |




