0 引言

粗糙集理论是波兰数学家Pawlak^[1]提出的能有效处理不精确、不一致和不完备数据的方法，目前，粗糙集理论已广泛用于机器学习、数据挖掘、特征选择等领域^[2-4]。从粒计算的角度看，经典的粗糙集模型是基于单粒度和单层次的，无法从多粒度、多层次的角度分析和处理问题。为了使粗糙集能够更好地解决实际问题，Qian等^[5]提出了多粒度粗糙集，在多粒度粗糙集中，目标决策可以通过多个粒度空间中的信息粒进行刻画，因此可以从多个角度、多个层次出发分析问题并获得更加满意、合理的求解。此后，许多学者提出了基于多粒度粗糙集的扩展粗糙集模型，例如，多粒度优势关系粗糙集、多粒度模糊关系粗糙集、邻域多粒度粗糙集、多粒度决策理论粗糙集、可变多粒度粗糙集等^[6-10]。这些多粒度粗糙集的扩展模型对粗糙集理论具有重要的推广作用。

在多粒度粗糙集中，粒度约简是一个重要问题，通过粒度约简能够在保持信息系统决策能力不变的前提下，选择一个无冗余的粒度空间子集。为了对多粒度粗糙集进行粒度约简，Qian等^[5]首先提出了启发式的粒度约简算法，该算法首先基于整个粒度空间对所有粒度按照粒度重要度大小进行排序，然后按序将粒度加入约简集直到获得一个粒度约简结果，但是该算法并没有给出每步粒度选取时的启发式函数，且在算法的最后并没有进一步对约简集进行冗余粒度的反向消除，获得的约简结果可能存在冗余粒度。张明等^[10]提出了可变多粒度粗糙集粒度约简算法，该算法在获得一个粒度约简集之后也没有进一步对约简集进行冗余粒度的反向消除，所以约简结果也可能存在冗余粒度。桑妍丽等^[11]发展了一种适合悲观多粒度粗糙集的粒度约简算法，虽然该算法效率较高，但并不适用于乐观多粒度粗糙集。此后，Yang等^[12]提出了一种多粒度粗糙集粒度约简的启发式算法，该算法能获得约简率较高的约简结果，但约简效率并不高。然而，在实际应用中，面对的往往是数据量很大的决策信息系统，此时，如何提高多粒度粗糙集粒度约简的效率就成为了一个关键问题。

为了提高多粒度粗糙集粒度约简的效率，本文定义了决策类下近似布尔矩阵，该矩阵能简化多粒度粗糙集粒度约简过程中决策类下近似的计算，基于该矩阵给出了计算决策类下近似算法和计算粒度重要度算法，并提出了粒度动态增加时快速计算粒度重要度算法来优化粒度约简过程中粒度重要度的计算。在此基础上，本文提出了一种多粒度粗糙集粒度约简的高效算法(Effective Algorithm for Granulation Reduction of Multi-granulation Rough Set, EAGRMRS)，最后通过实验验证了本文所提算法的有效性和高效性。

1 相关概念

在本章，介绍本文用到的相关知识。

定义1  四元组IS=(U, AT, V, f)是一个信息系统，其中：U为对象的非空有限集合，即论域；AT为属性的非空有限集合；$V = \bigcup\limits_{a \in AT} {{V_a}} $，V_a是属性a∈AT的值域；f:U×AT→V是一个信息函数，它为每个对象的每个属性赋予一个信息值，即$\forall a \in AT $，x∈U，f(x, a)∈V_a。如果AT=C∪D，C是条件属性的集合，D是决策属性的集合，则DIS=(U, C∪D, V, f)称为决策信息系统。

定义2^[5]  设信息系统IS=(U, AT, V, f)，B⊆AT，对于X⊆U，X的下、上近似集合和边界域定义为：

$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{B} \left( X \right) = \left\{ {x \in U|{{\left[x \right]}_B} \subseteq X} \right\} $

(1)

$ \overline B \left( X \right) = \left\{ {x \in U\left| {{{\left[x \right]}_B} \cap X \ne \emptyset } \right.} \right\} $

(2)

$ BN{D_B}\left( X \right) = \overline B \left( X \right)-\underline B \left( X \right) $

(3)

其中[x]_B是x在B上的等价类。

当$BN{D_B}\left( X \right) = \emptyset $，即B(X)=B(X)时，称X在信息系统中是可以定义的，否则称X是粗糙的。X的正域POS_B(X)=B(X)，X的负域NEG_B(X)=U-B(X)。

为了能够从多粒度、多层次的角度分析和处理问题，Qian等^[5]提出了多粒度粗糙集。本文中用上标O(Optimistic)表示乐观的语义，用上标P(Pessimistic)表示悲观的语义，以此来区分乐观多粒度粗糙集和悲观多粒度粗糙集。

定义3^[5]  设信息系统IS=(U, AT, V, f)，A={A₁, A₂, …, A_m}是AT的m个属性子集族。对于$\forall X \subseteq U $，X关于A的乐观多粒度下近似和乐观多粒度上近似分别定义如下：

$ \begin{gathered} {\underline {\sum\limits_{i = 1}^m {{A_i}} } ^{\rm{O}}}\left( X \right) = \left\{ {x:{{\left[x \right]}_{{A_1}}} \subseteq X \vee } \right. \hfill \\ \;\;\;\;\;\;\;\;{\left[x \right]_{{A_2}}} \subseteq X \vee \cdots \left. { \vee {{\left[x \right]}_{{A_m}}} \subseteq X, x \in U} \right\} \hfill \\ \end{gathered} $

(4)

$ {\overline {\sum\limits_{i = 1}^m {{A_i}} } ^{\text{O}}}\left( X \right) = \sim \left( {{{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\text{O}}}\left( { \sim X} \right)} \right) $

(5)

定义4^[5]  设信息系统IS=(U, AT, V, f)，A={A₁, A₂, …, A_m}是AT的m个属性子集族。对于$\forall X \subseteq U $，X关于A的悲观多粒度下近似和悲观多粒度上近似分别定义如下：

$ \begin{gathered} {\underline {\sum\limits_{i = 1}^m {{A_i}} } ^{\rm{P}}}\left( X \right) = \left\{ {x:{{\left[x \right]}_{{A_1}}} \subseteq X \wedge {{\left[x \right]}_{{A_2}}} \subseteq X \wedge \cdots \wedge } \right. \hfill \\ \left. {{{\left[x \right]}_{{A_m}}} \subseteq X, x \in U} \right\} \hfill \\ \end{gathered} $

(6)

$ {\overline {\sum\limits_{i = 1}^m {{A_i}} } ^{\text{P}}}\left( X \right) = \sim \left( {{{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\text{P}}}\left( { \sim X} \right)} \right) $

(7)

定义5^[13]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，决策属性D导出的划分为U/D={X₁, X₂, …, X_r}。用粒度集A表示U/D的近似质量(也称为依赖度)，定义为：

$ \gamma \left( {A,D} \right){\text{ = }}\sum\limits_{j = 1}^r {\left\{ {\left| {{{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\text{O}}}\left( {{X_j}} \right)} \right|:{X_j} \in U/D} \right\}\left| U \right|} $

(8)

2 多粒度粗糙集的粒度约简

目前，为了满足不同的需要，已经有许多不同的约简定义^[14-16]被提出，一个常用的定义是保持决策信息系统的正域不变。

定义6 ^[11]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，决策属性D导出的划分为U/D={X₁, X₂, …, X_r}，则基于A的乐观下近似分布函数定义如下：

$ \underline D _A^{\rm{O}} = \left( {{{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\rm{O}}}\left( {{X_1}} \right), {{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\rm{O}}}({X_2}), \cdots, {{\underline {\sum\limits_{i = 1}^m {{A_i}} } }^{\rm{O}}}({X_r})} \right) $

(9)

若D_A^O=D_C^O，则称A是C的粒度乐观下近似分布一致集。粒度下近似分布一致集保持每个目标决策的下近似不变，即可保持分类的不变。

定义7^[11]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，决策属性D导出的划分为U/D={X₁, X₂, …, X_r}，若A是C的粒度乐观下近似分布一致集，且对$\forall A' \subset A $，都有D_A′^O≠D_C^O，则称A是C的粒度乐观下近似分布约简。

定义8^[11]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，给定粒度集A′，$\emptyset \subset A' \subseteq A $，X∈U/D。

若${\underline {\sum\limits_{{A_i} \in A} {{A_i}} } ^{\rm{O}}}\left( X \right){\rm{ = }}{\underline {\sum\limits_{{A_i} \in A, {A_i} \notin A'} {{A_i}} } ^{\rm{O}}}\left( X \right) $，则称A′在A中关于X是不重要的；

若${\underline {\sum\limits_{{A_i} \in A} {{A_i}} } ^{\rm{O}}}\left( X \right) \ne {\underline {\sum\limits_{{A_i} \in A, {A_i} \notin A'} {{A_i}} } ^{\rm{O}}}\left( X \right) $，则称A′在A中关于X是重要的。

定理1^[11]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，A′⊆A，则：

$ \underline {{A_i}} \left( X \right) \subseteq {\underline {\sum\limits_{{A_i} \in A'} {{A_i}} } ^{\rm{O}}}\left( X \right) \subseteq {\underline {\sum\limits_{{A_i} \in A} {{A_i}} } ^{\rm{O}}}\left( X \right) $

根据定义3，该定理显然成立。由该定理可知，在乐观多粒度粗糙集中，随着粒度空间的增大，下近似中对象的个数增加。在悲观多粒度粗糙集中，也可以得出类似的结论，随着粒度空间的增大，下近似中对象的个数减少。因此，可以利用下近似中对象个数的变化来衡量粒度的重要性。

定义9^[12]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族。

1) A′⊆A，∀A_i∈A′，定义在粒度集A′上，A_i关于D的粒度重要度为：

$ Si{g_{{\rm{in}}}}({A_i}, A', D) = {\rm{abs}}(\gamma (A', D)-\gamma (A'-{A_i}, D)) $

(10)

2) A′⊆A，∀A_i∈A－A′，定义在粒度集A′上，A_i关于D的粒度重要度为：

$ Si{g_{{\rm{out}}}}({A_i}, A', D){\rm{ = abs}}(\gamma ({A_i} \cup A', D)-\gamma (A'{\rm{, }}D)) $

(11)

其中：abs(N)表示N的绝对值。在粒度约简的过程中，一般以粒度重要度为启发来设计粒度约简算法。

3 多粒度粗糙集粒度约简的高效算法 3.1 决策类下近似布尔矩阵

粒度约简中计算粒度重要度时要多次求不同粒度集合下决策类的下近似，为了将过多且有重复的集合运算转换为布尔运算来提高效率，本文定义了决策类下近似布尔矩阵并给出了根据决策信息系统求决策类下近似布尔矩阵的算法。

定理2  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，决策属性D导出的划分为U/D={X₁, X₂, …, X_r}，若x∈X_k，则$x \notin \underline {{A_j}} \left( {U-{X_k}} \right)\left( {k \in \left\{ {1, 2, \cdots, r} \right\}} \right) $。

该定理显然成立，对于∀x∈U，x仅可能属于决策类X_k(x∈X_k)的下近似，也就是说x最多属于一个决策类的下近似。

定义10  设决策信息系统DIS=(U, C∪D, V, f)，U={x₁, x₂, …, x_n}, A={A₁, A₂, …, A_m}是C的m个属性子集族，决策属性D导出的划分为U/D={X₁, X₂, …, X_r}，定义决策类下近似布尔矩阵为M=(M_m(i, j)), 其中M_m(i, j)表示第i行第j列的元素(1≤i≤n, 1≤j≤m)，元素定义如下：

$ M\_m\left( {i, j} \right) = \left\{ \begin{gathered} 0, \;\;\;\;{x_i} \notin \underline {{A_j}} \left( {{X_k}} \right) \hfill \\ 1, \;\;\;\;{x_i} \in \underline {{A_j}} \left( {{X_k}} \right) \hfill \\ \end{gathered} \right. $

(12)

其中x_i∈X_k(k∈{1, 2, …, r})。

决策类下近似布尔矩阵包含|U|行、|A|列，|U|表示决策信息系统中的实例数，|A|表示粒度集合大小。

显然，决策信息系统的决策类下近似布尔矩阵包含了所有对象在每个粒度上是否属于对应决策类下近似的信息。这样，求某个决策类在某个粒度集合上的下近似时我们只需要进行布尔矩阵元素的0、1判断，不需要再进行集合运算。因此，该矩阵可将粒度约简中的集合运算转化为布尔运算。以完备决策信息系统为对象，本文给出计算决策类下近似布尔矩阵的算法。

算法1  计算决策类下近似布尔矩阵算法。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}；

输出 下近似布尔矩阵M。

1)  设置$\mathit{\boldsymbol{M}} \leftarrow \emptyset $，i←1，j←1；

2)  计算U/D={X₁, X₂, …, X_r}；

3)  For i=1 to |U|

  For j=1 to m

   If [x_i]_Aj⊆X_k

    M_m(i, j)=1；

   Else

    M_m(i, j)=0；

   Endif

  Endfor

 Endfor

4)  输出M。

该算法的复杂度为O(|A|·|U|²)，建立了上述决策类下近似布尔矩阵以后，粒度约简算法中计算粒度重要度时，可以基于该矩阵快速计算决策类在任意粒度上的下近似，这个过程只需要简单地判断矩阵中元素M_m(i, j)的取值。若M_m(i, j)=0，则对象x_i在粒度A_j上不属于x所在决策类X_k的下近似; 若M_m(i, j)=1，则对象x_i在粒度A_j上属于x所在决策类X_k的下近似，避免了过多并且耗时的集合运算。

下面以文献[17]中的决策信息系统为例，说明构建决策类下近似布尔矩阵的过程。

例1  给定一个决策信息系统DIS=(U, C∪D, V, f), 如表 1所示，其中:U={x₁, x₂, x₃, x₄, x₅, x₆}为对象集，A={{a₁}, {a₂}, {a₃}, {a₄}, {a₅}, {a₆}}为粒度空间。

首先，根据决策属性导出划分为U/D={{x₁, x₂, x₃}, {x₄, x₅, x₆}}，令X₁={x₁, x₂, x₃}，X₂={x₄, x₅, x₆}。

然后，对于每个对象x_i计算其在每个粒度{a_j}上的等价类[x]_{aj}并判断是否包含于对应的决策类，若是，设置矩阵M对应的位置M_m(i, j)=1，否则设置M_m(i, j)=0。对于对象x₁，[x₁]_{a1}={x₁, x₃, x₅, x₆}⊄X₁，设置M_m(1, 1)=0；[x₁]_{a2}={x₁, x₅}⊄X₁，设置M_m(1, 2)=0；[x₁]_{a3}={x₁, x₃, x₄, x₅}⊄X₁，设置M_m(1, 3)=0；[x₁]_{a4}={x₁, x₄, x₅, x₆}⊄X₁，设置M_m(1, 4)=0；[x₁]_{a5}={x₁, x₄, x₅, x₆}⊄X₁，设置M_m(1, 5)=0；[x₁]_{a6}={x₁, x₂, x₃}⊂X₁，设置M_m(1, 6)=1。类似，可以计算出x₂，x₃，x₄，x₅，x₆在粒度{a₁}，{a₂}，{a₃}，{a₄}，{a₅}，{a₆}上的等价类并判断是否包含于对应的决策类，最终，可以建立如下决策信息系统的决策类下近似布尔矩阵：

$ {M_{\left| U \right| \times \left| A \right|}} = \left[{\begin{array}{*{20}{c}} 0&0&0&0&0&1 \\ 0&0&0&1&1&1 \\ 0&0&0&1&1&1 \\ 0&0&0&0&0&1 \\ 0&0&0&0&0&1 \\ 0&0&0&0&0&1 \end{array}} \right] $

接下来以乐观多粒度粗糙集为例，给出基于决策类下近似布尔矩阵计算决策类下近似算法和基于决策类下近似布尔矩阵计算粒度重要度算法。

算法2  基于决策类下近似布尔矩阵计算决策类下近似算法。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}，X_k∈U/D，决策类下近似布尔矩阵M=(M_m(i, j))；

输出 X_k的下近似集合L。

1)  设置$L \leftarrow \emptyset $，j←1；

2)  ∀x_i∈X_k，

 For j=1 to m

  If M_m(i, j)=1

   L←L∪{x_i}，break；

  Endif

 Endfor

3)  输出L。

然后利用算法2计算决策类下近似，根据定义9易得下面乐观多粒度粗糙集基于决策类下近似布尔矩阵计算粒度重要度算法。

算法3  基于决策类下近似布尔矩阵计算粒度重要度算法。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}，决策属性D导出的划分U/D={X₁, X₂, …, X_r}，决策类下近似布尔矩阵M=(M_m(i, j))，A′⊆A，∀A_i∈A；

输出 在粒度集A′上，A_i关于D的粒度重要度Sig^O。

1)  设置$D' \leftarrow \emptyset $，$D'' \leftarrow \emptyset $，k←1；

2)  For k=1 to r

  利用算法2计算${\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

  $D' = D' \cup {\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

 Endfor

3)  If A_i⊆A′

  A″=A′－A_i；

 Else

  A″=A′∪A_i；

 For k=1 to r

  利用算法2计算${\underline {\sum\limits_{{A_j} \in A''} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

  $D'' = D'' \cup {\underline {\sum\limits_{{A_j} \in A''} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

 Endfor

4)  基于D′和D″，根据定义9计算Sig^O；

5)  输出Sig^O。

3.2 快速计算粒度重要度算法

文献[18]中对粒度动态变化时如何快速计算某个对象集的下、上近似进行了研究，提出了一个在粒度动态变化时快速计算下、上近似的算法。而在粒度约简算法中，选取当前重要度最大的粒度加入约简集，就涉及粒度动态增加时计算决策类的下近似，基于决策类下近似布尔矩阵，参考文献[18]可以设计算法来优化计算粒度重要度过程中决策类下近似的计算。

定理3 ^[18]  设决策信息系统DIS=(U, C∪D, V, f)，A={A₁, A₂, …, A_m}是C的m个属性子集族，X⊆U, 有：

$ {\underline {\sum\limits_{j = 1}^m {{A_j}} } ^{\rm{O}}}\left( X \right) = {\underline {\sum\limits_{j = 1}^{m- 1} {{A_j}} } ^{\rm{O}}}\left( X \right) \cup \left\{ {x \notin {{\underline {\sum\limits_{j = 1}^{m- 1} {{A_j}} } }^{\rm{O}}}\left( X \right):{{\left[x \right]}_{{A_m}}} \subseteq X} \right\} $

(13)

$ {\underline {\sum\limits_{j = 1}^m {{A_j}} } ^{\rm{P}}}\left( X \right) = {\underline {\sum\limits_{j = 1}^{m- 1} {{A_j}} } ^{\rm{P}}}\left( X \right)- \left\{ {x \in {{\underline {\sum\limits_{j = 1}^{m- 1} {{A_j}} } }^{\rm{P}}}\left( X \right):{{\left[x \right]}_{{A_m}}} \not\subset X} \right\} $

(14)

该定理表明，在乐观多粒度粗糙集中，若已知粒度空间{A₁, A₂, …, A_m－1}上对象集X的下近似为${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{O}}}\left( X \right) $，当新增加一个粒度A_m时，重新计算X的下近似只需计算${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{O}}}\left( X \right) $之外的对象在粒度A_m上是否属于X的下近似，若是，则将其并入${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{O}}}\left( X \right) $即可；在悲观多粒度粗糙集中，若已知粒度空间{A₁, A₂, …, A_m－1}上对象集X的下近似为${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{P}}}\left( X \right) $，当新增加一个粒度A_m时，重新计算X的下近似只需计算${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{P}}}\left( X \right) $中的对象在粒度A_m上是否属于X的下近似，若否，则将其从${\underline {\sum\limits_{j = 1}^{m-1} {{A_j}} } ^{\rm{P}}}\left( X \right) $中移除即可。

以乐观多粒度粗糙集为例，基于决策类下近似布尔矩阵，根据定理3给出粒度动态增加时快速计算决策类下近似算法和粒度动态增加时快速计算粒度重要度算法。

算法4  粒度动态增加时快速计算决策类下近似算法。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}，决策类X_k∈U/D，决策类下近似布尔矩阵M=(M_m(i, j))，粒度空间A′⊆A上X_k的下近似${\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $，一个新增加的粒度∀A_i∈A－A′；

输出 ${\underline {\sum\limits_{{A_j} \in A' \cup {A_i}} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $。

1)  ${\underline {\sum\limits_{{A_j} \in A' \cup {A_i}} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) = {\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

2)  对于$\forall {x_t} \notin {\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $且x_t∈X_k，

 If M_m(t, i)=1

  ${\underline {\sum\limits_{{A_j} \in A' \cup {A_i}} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) = {\underline {\sum\limits_{{A_j} \in A' \cup {A_i}} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) + \left\{ {{x_t}} \right\} $；

 Endif

3)  输出${\underline {\sum\limits_{{A_j} \in A' \cup {A_i}} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $。

基于算法4，得出如下粒度动态增加时快速计算粒度重要度的算法。

算法5  粒度动态增加时快速计算粒度重要度算法。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}，决策属性D导出的划分U/D={X₁, X₂, …, X_r}，决策类下近似布尔矩阵M=(M_m(i, j))，粒度空间A′⊆A上决策类下近似构成的集合$ \underline D _{A'}^{\rm{O}} = \left\{ {{{\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } }^{\rm{O}}}\left( {{X_1}} \right), {{\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } }^{\rm{O}}}\left( {{X_2}} \right)} \right., \cdots, \left. {{{\underline {\sum\limits_{{A_j} \in A'} {{A_j}} } }^{\rm{O}}}\left( {{X_r}} \right)} \right\}, \forall {A_i} \in A-A'$；

输出 在粒度集A′上，A_i关于D的粒度重要度Sig^O。

1)  设置$A'' \leftarrow \emptyset, D_{A''}^{\rm{O}} \leftarrow \emptyset $；

2)  A″=A′∪A_i；

 For k=1 to r

  基于D_A′^O，利用算法4计算${\underline {\sum\limits_{{A_j} \in A''} {{A_j}} } ^{\rm{O}}}\left( {{X_k}} \right) $；

  $\underline D _{A''}^{\rm{O}} = \underline D _{A''}^{\rm{O}} \cup \left\{ {{{\underline {\sum\limits_{{A_j} \in A''} {{A_j}} } }^{\rm{O}}}\left( {{X_k}} \right)} \right\} $

 Endfor

3)  基于D_A′^O和D_A″^O，根据定义9计算Sig^O；

4)  输出Sig^O。

悲观多粒度粗糙集中快速计算粒度重要度算法类似，在此不再赘述。

3.3 EAGRMRS

粒度约简算法的基本过程如下：首先获得一个原始粒度空间下不可除去的粒度集合(粒度约简核)，然后以这个粒度集为起点，以粒度重要度为启发，每次选择当前粒度空间下最为重要的粒度加入到约简粒度集中，直到其下近似分布与原始粒度空间下近似分布一致。

算法6  多粒度粗糙集粒度约简的高效算法(EAGRMRS)。

输入 决策信息系统DIS=(U, C∪D, V, f)，粒度空间A={A₁, A₂, …, A_m}，决策属性D导出的划分U/D={X₁, X₂, …, X_r}；

输出 粒度约简集RED^O。

1)  设置$RE{D^{\rm{O}}} \leftarrow \emptyset $；

2)  利用算法1建立决策类下近似布尔矩阵M；

3)  对于∀A_i∈A，利用算法3计算Sig_in(A_i, A, D)，

 If Sig_in(A_i, A, D)≠0

  RED^O=RED^O∪A_i；

 Endif

 令CORE^O=RED^O；

4)  利用算法2计算粒度集合RED^O上的决策类下近似构成的集合$\underline {D_{RE{D^{\rm{O}}}}^{\rm{O}}} $；

 Do

  ∀A_i∈A－RED^O，基于$\underline {D_{RE{D^{\rm{O}}}}^{\rm{O}}} $，利用算法5计算Sig_out(A_i, RED^O, D)；

  If Sig_out(A_k, RED^O, D)=max{Sig_out(A_i, RED^O, D):A_i∈ A－RED^O}

   RED^O=RED^O∪A_k；

   更新$\underline {D_{RE{D^{\rm{O}}}}^{\rm{O}}} $；

  Endif

 Until γ(RED^O, D)=γ(A, D)；

5)  ∀A_i∈RED^O－CORE^O

 If γ(RED^O－A_i, D)=γ(A, D)

  RED^O=RED^O－A_i；

 Endif

6)  输出RED^O。

算法复杂度分析：第2)步时间复杂度为O(|A|·|U|²)，第3)步时间复杂度为O(|A|²·|U|)，第4)步时间复杂度为O(|A|²·|U|)，所以算法6的时间复杂度为O(|A|·|U|²+|A|²·|U|)。悲观多粒度粗糙集粒度约简的高效算法与乐观多粒度粗糙集粒度约简的高效算法类似。

4 实验结果与分析

文献[12]提出了一种多粒度粗糙集粒度约简的启发式算法(Heuristic Approach to Granular Structure Selection, HAGSS)，其中计算决策类下近似可以参考文献[5]。将本文所提算法EAGRMRS与算法HAGSS进行比较，比较两种算法的运行效率以及运行效率与数据集包含的数据量的关系。

选用UCI机器学习库中的4个数据集进行测试，数据集具体信息见表 2，其中：数据集Zoo、Chess是完备的，数据集Audiology、Mushroom有缺失的属性值，是不完备的。对于不完备的数据集等价关系将不再适用，本文中用容差关系来处理不完备的数据集^[14]。

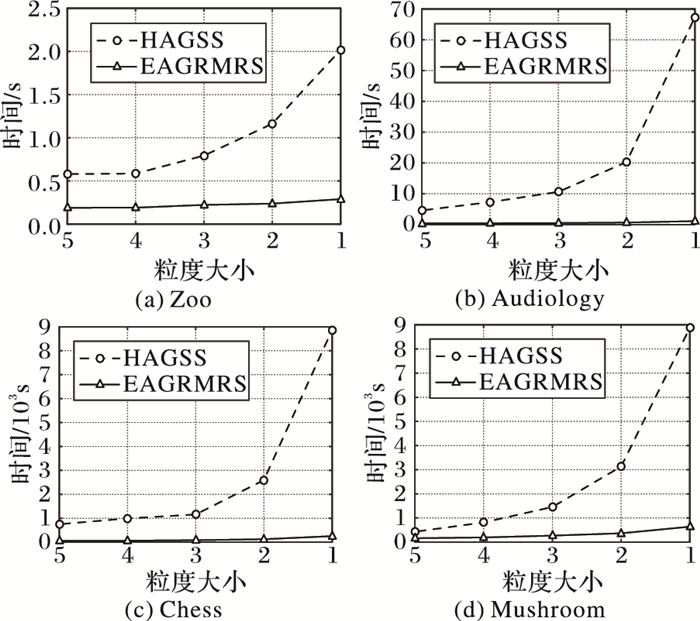
多粒度粗糙集中一个粒度可能包含多个属性，为了模拟多粒度的情况，对于表 2中的数据集，从第一个属性开始，分别以每1、2、3、4、5个属性构成一个粒度，若数据集的条件属性个数不能被1、2、3、4、5整除，最后余下的属性构成一个粒度，实验结果如图 1所示。

粒度大小就是构成一个粒度的属性个数，对于同一个数据集，因为条件属性一定，所以当选取的粒度大小越大，所组成的粒度空间就越小。从图 1中可以看出，在所有数据集上，算法EAGRMRS进行粒度约简的运行时间均少于算法HAGSS，且随着粒度大小变小，也就是粒度空间变大时，HAGSS运行效率下降较为明显，而算法EAGRMRS运行效率较为稳定。所以，本文所提算法在约简效率和稳定性方面都优于算法HAGSS。

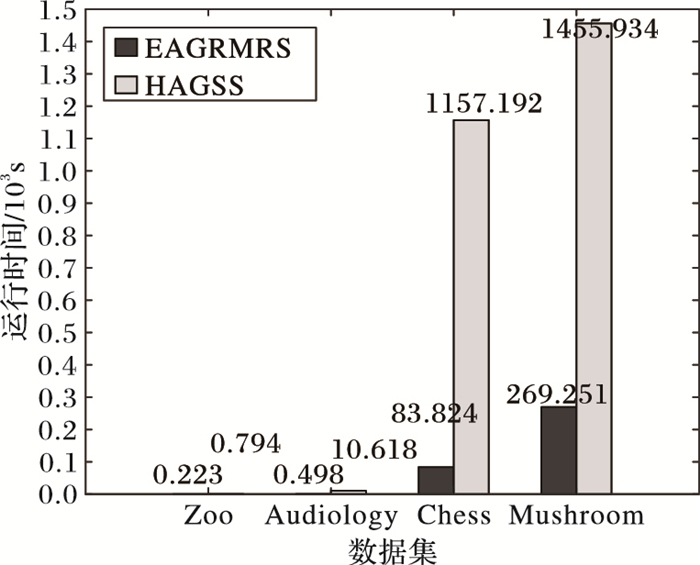
接下来，为了比较算法EAGRMRS和算法HAGSS的约简效率与数据集包含的数据量的关系，取粒度大小为3时，四个数据集的约简时间如图 2所示。

由表 2可知，编号为1、2、3、4的数据集包含的数据量是递增的，由图 2可知，随着数据集包含的数据量越大，算法HAGSS的运行时间增加得较快，而算法EAGRMRS的运行时间增加较慢，所以在对数据量较大的决策信息系统进行粒度约简时，本文所提算法效率优势将更加明显。

5 结语

本文以决策信息系统为对象，定义了决策信息系统决策类下近似布尔矩阵，该矩阵能简化多粒度粗糙集粒度约简过程中决策类下近似的计算，基于该矩阵给出了计算决策类下近似算法和计算粒度重要度算法。此外，针对计算粒度重要度时存在冗余计算，基于决策类下近似布尔矩阵提出了粒度动态增加时快速计算粒度重要度算法，在此基础上，提出了一种多粒度粗糙集粒度约简的高效算法(EAGRMRS)。在UCI数据集上的实验结果验证了本文所提算法的有效性和高效性。粒度约简能够获得保持决策信息系统决策能力不变的粒度空间子集，如何在粒度约简之后对每个粒度中的属性进行进一步的约简，并对约简后的决策信息系统进行规则提取是接下来要研究的问题。