0 引言

压缩感知(Compressed Sensing, CS)^[1-3]技术因其高效的信息采样机制，已被广泛应用到信道估计、神经网络、雷达信号处理、核磁共振成像等领域。传统压缩感知技术采用非自适应的观测过程，即通过预先设计观测矩阵并对信号进行一次性观测，观测向量的能量均匀分配，这样做使得观测向量每次都对整个信号域观测，感知能量大部分被用来观测不含非零元素的位置，造成能量利用效率和抗噪性能不高。

为了提高传统CS算法的能量效率和抗噪性能，研究者们对自适应压缩感知(Adaptive CS, ACS)展开了一系列研究，其主要思想是根据以前的观测值自适应地设计下一步的观测向量，可在观测过程中剔除一些非支撑坐标，使感知能量集中在含有支撑坐标的少数位置。目前的一些典型的自适应算法主要分别从提高观测信噪比或优化观测矩阵出发考虑，并未将两者有机地结合。贝叶斯压缩感知(Bayesian Compressed Sensing, BCS)^[4-5]在相关向量机的基础上，根据贝叶斯推断和最小微分熵来指导设计下一步观测向量，由于高维求逆，导致计算量较大。文献[6]建立一种信息贪婪(Info-Greedy)自适应压缩感知框架，观测向量设计依据最大化当前观测值与信号相对于以前的观测值的最大条件互信息增益，需要信号概率分布的参数先验。BCS和文献[6]中算法所设计的新观测向量均具有随机性，这可能导致每步的信噪比增益不稳定，并且具有较高的复杂度。文献[7]考虑数据间的关联性，提出一种利用信号自相关性的自适应观测方案。文献[8]考虑到实际应用的物理约束，预先设置观测池，提出一种能够根据支撑集估计情况自适应地从观测池中选择原子的感知方案。文献[9]从动态规划的角度利用粒子群算法设计了一种观测矩阵更新机制。文献[10]在生物信息研究中提出可自适应选择基向量的动态旋钮框架。上述各自适应算法虽然从提高观测信噪比的角度实现了较好的抗噪恢复性能，但未考虑优化观测矩阵本身所能带来的性能增益。文献[11-13]在连续观测过程中，将Gram矩阵向对角阵优化，通过迭代收缩Gram矩阵非对角元素，完成对观测矩阵的优化，有效提高了信号重构概率和抗噪性能；但这些算法未考虑提高观测信噪比可能带来的性能增益。

综上，自适应观测与优化观测矩阵均能提高传统CS算法的重构精度。为综合利用这二者的优势，并提高传统CS算法的能量利用效率和抗噪性能，本文设计一种自适应观测机制，将观测能量集中估计支撑集的位置，以提高观测信噪比，同时将Gram矩阵向对角阵优化，以减小其他位置的干扰。仿真实验结果表明，本文所提观测机制可有效提高观测信噪比，减小非对角元素能量，并且能够有效改善传统CS重构算法的抗噪性能。

1 压缩感知基本理论

假设信号x仅有K个非零元素，其他元素均为0，则称信号x是K-稀疏的，并定义信号x的支撑集：

$ \mathit{\Lambda} = \left\{ {i|{x_i} \ne 0} \right\} $

(1)

其中：x_i为信号x的第i个元素，易知|Λ|=K，此处|·|表示集合中元素的个数。若信号并非稀疏，如果可将信号在某个变换域Ψ展开，即x=Ψc，若变换系数c是稀疏的，则仍可应用压缩感知理论。

设观测矩阵为Φ，观测过程可表示为：

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} + \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} c}} + \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} c}} + \mathit{\boldsymbol{w}} $

(2)

其中：Θ=ΦΨ称为感知矩阵；w~N(0, σ_w²)为高斯观测噪声。常见的CS恢复算法有正交匹配追踪(Orthogonal Matching Pursuit, OMP)^[14]、子空间追踪(Subspace Pursuit, SP)^[15]和基追踪(Basic Pursuit, BP)^[1]等。

2 利用观测矩阵优化的自适应观测 2.1 理论推导

为简化分析，假设原信号x是稀疏的，那么Θ=Φ。根据文献[3]易知，若Gram矩阵G=Φ^TΦ近似于对角阵(假设此对角阵为单位阵I，即有G≈I)，G的列具有正交性，此时其互相干系数μ(G)=0，则观测矩阵Φ是理想的。设Φ=[A^T  a]^T∈R^(M+1)×N，其中矩阵A∈R^M×N是当前使用的观测矩阵，向量a∈R^N×1是所要设计的下一步观测向量。若约束每个观测向量的能量为‖a‖₂²=a^Ta=1，则观测矩阵优化问题可描述为：

$ \mathop {\arg \min }\limits_\boldsymbol{a} \frac{1}{2}\left\| {{\boldsymbol{\Phi }^{\rm{T}}}\boldsymbol{\Phi } - \boldsymbol{I}} \right\|_{\rm{F}}^2 $

(3)

s.t. a^Ta=1

将Φ=[A^T  a]^T代入(3)，可得：

$ \mathop {\arg \min }\limits_\boldsymbol{a} \frac{1}{2}\left\| {{\boldsymbol{A}^{\rm{T}}}\boldsymbol{A} + \boldsymbol{a}{\boldsymbol{a}^{\rm{T}}} - \boldsymbol{I}} \right\|_{\rm{F}}^2 $

(4)

s.t. a^Ta=1

其中‖·‖_F表示Frobenius范数。利用拉格朗日乘子法，式(4)等价于：

$ \mathop {\arg \min }\limits_\boldsymbol{a} J\left( \mathit{\boldsymbol{a}} \right) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A + a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}-\mathit{\boldsymbol{I}}} \right\|_{\rm{F}}^2 + \mathit{\boldsymbol{\lambda }}\left( {1-{\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{a}}} \right) $

(5)

其中λ是拉格朗日常数。式(5)中代价函数对向量a求导，可得：

$ \begin{array}{l} \frac{{\partial J\left( \mathit{\boldsymbol{a}} \right)}}{{\partial \mathit{\boldsymbol{a}}}} =- 2\mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{a}}^{\rm{T}}} + \\ \frac{1}{2}\frac{\partial }{{\partial \mathit{\boldsymbol{a}}}}\left[{{\rm{tr}}{{\left\{ {{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\bf{T}}}-\mathit{\boldsymbol{I}}} \right\}}^{\bf{T}}}\left( {{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\bf{T}}}-\mathit{\boldsymbol{I}}} \right)} \right] = \\ 2{\mathit{\boldsymbol{a}}^{\bf{T}}}\left( {{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} -\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\bf{T}}}} \right) -2\mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{a}}^{\bf{T}}} = \\ 2\left( {{\mathit{\boldsymbol{a}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} -{\mathit{\boldsymbol{a}}^{\rm{T}}} + {\mathit{\boldsymbol{a}}^{\bf{T}}}\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\bf{T}}}} \right) - 2\mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{a}}^{\bf{T}}}\mathop = \limits^{{\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{a}} = 1} \\ 2\left( {{\mathit{\boldsymbol{a}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{a}}^{\rm{T}}} + {\mathit{\boldsymbol{a}}^{\bf{T}}}} \right) - 2\mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{a}}^{\bf{T}}} = \\ 2\left( {{\mathit{\boldsymbol{a}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{\lambda }}{\mathit{\boldsymbol{a}}^{\rm{T}}}} \right) \end{array} $

(6)

其中tr{·}表示矩阵的迹，令式(6)等于0，则可得：

$ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Aa}} = \mathit{\boldsymbol{\lambda a}} $

(7)

即下一步观测向量a是Gram矩阵A^TA对应于特征值λ的特征向量：

$ \mathit{\boldsymbol{a}} = {\mathit{\boldsymbol{u}}_i};\;\;i = 1, 2, \cdots, N $

(8)

其中，u_i为对应于特征值λ_i的特征向量。因为A^TA是奇异的，即rank(A^TA)=M < N，其最小的N－M个特征值对应的特征向量构成干扰空间，若新的观测向量属于此空间，势必会对观测矩阵优化产生不利影响。因此新观测向量应设计为：

$ \mathit{\boldsymbol{a}} = {\mathit{\boldsymbol{u}}_i};\;\;\;i = 1, 2, \cdots, M $

(9)

将式(9)代入式(5)，可得：

$ \begin{array}{l} {J_{\min }} = \frac{1}{2}\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}-\mathit{\boldsymbol{I}}} \right\|_{\rm{F}}^2 + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}{\rm{tr}}\left\{ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Aa}}{\mathit{\boldsymbol{a}}^{\rm{T}}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}-\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}} \right\} = {J_0} + \mathit{\boldsymbol{\lambda }}-\frac{1}{2} \end{array} $

(10)

其中${J_0} = \frac{1}{2}\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}-\mathit{\boldsymbol{I}}} \right\|_{\rm{F}}^2 $为常数，表示未使用新观测向量时的代价函数。易知当λ最小时，J(a)有最小值，因此下一步观测向量设计为A^TA最小非零特征值对应的特征向量。

Gram矩阵A^TA是一个N×N的矩阵，对其进行特征分解运算量很大，也无法提高观测信噪比。为有效提高观测信噪比，本文考虑通过传统CS恢复算法获得估计支撑集，继而将能量集中在这些位置，对其他位置不分配能量。一般说来，因为估计支撑集中含有支撑坐标，对其分配更多的能量符合自适应观测的思想。假设某次观测的估计支撑集为$\mathit{\tilde {\Lambda}} $，且$\left| \mathit{\tilde {\Lambda}} \right| = K $，则新观测向量设计为:

$ \mathit{\boldsymbol{\varphi }} = \left( {{\mathit{\boldsymbol{a}}^{\bf{T}}}\;\;\;{\bf{0}}} \right) \in {{\bf{R}}^{1 \times N}} $

(11)

其中a∈R^K×1且‖a‖₂²=1为新观测向量的非零部分。

设观测矩阵$\mathit{\boldsymbol{ \boldsymbol{\varPhi} = }}\left[\begin{array}{l} \mathit{\boldsymbol{A}}\;\;\;\mathit{\boldsymbol{B}}\\ {\mathit{\boldsymbol{a}}^{\bf{T}}}\;\;{\mathit{\boldsymbol{b}}^{\bf{T}}} \end{array} \right] \in {{\bf{R}}^{\left( {M + 1} \right) \times N}} $，其中:A∈R^M×K为原观测矩阵中坐标在集合$\mathit{\tilde {\Lambda}} $中的列组成的子矩阵; B∈R^M×(N-K)为原观测矩阵中剩余的列组成的子矩阵。新观测向量φ=(a^T  b^T)∈R^1×N，其中a∈R^K×1，b∈R^(N-K)×1，于是式(3)可转化为如下问题：

$ \mathop {\arg \min }\limits_\boldsymbol{a} \frac{1}{2}\left\| {\left[\begin{array}{l} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}\;\;\;{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{b}}^{\rm{T}}}\\ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{b}}{\mathit{\boldsymbol{a}}^{\rm{T}}}\;\;\;{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{b}}{\mathit{\boldsymbol{b}}^{\rm{T}}} \end{array} \right] -\mathit{\boldsymbol{I}}} \right\|_{\rm{F}}^2 $

(12)

s.t. a^Ta+b^Tb=1

其中，I为N×N的单位矩阵。为完成自适应观测，设置b=0，这相当于把全部能量都分配到估计支撑位置，估计支撑集中可能含有少量非支撑坐标，这些非支撑坐标会获得少量能量分配，这种分配方式相比将能量分配在整个信号域的方案获得信噪比增益高很多；并且，由于噪声观测值的随机性，在后续观测中这些坐标将会被逐步取代。于是式(12)化简为：

$ \mathop {\arg \min }\limits_\boldsymbol{a} \frac{1}{2}\left\| {\left[\begin{array}{l} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}-{\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{A}}}\;\;\;{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}}\\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{A}}\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{B}}} \end{array} \right]} \right\|_{\rm{F}}^2 $

(13)

s.t. a^Ta=1

其中, I_A∈R^K×K、I_B∈R^{(N－K)×(N－K)}表示单位阵，又a只影响A^TA+aa^T－I_A, 从而式(13)等价于：

$ \mathop {\arg \min }\limits_\boldsymbol{a} \frac{1}{2}\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{T}}}-{\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{A}}}} \right\|_{\rm{F}}^2 $

(14)

s.t. a^Ta=1

问题式(14)与式(4)具有相同的形式，易知其解为：

$ \mathit{\boldsymbol{a = u}} $

(15)

因为A^TA是满秩的，可知u为Gram矩阵A^TA的最小特征值对应的特征向量。于是可知，新观测向量的支撑集为$\mathit{\tilde {\Lambda}} $，非零项的值为u，这表明如果按照式(11)的方式分配观测能量、以式(15)的方式设计新观测向量可使J(a)最小。

2.2 自适应观测机制

若考虑将a设计为随机观测向量，每次观测仍将能量全部分配给a，这样仍能带来观测信噪比的增益，但a的随机性并不能保证它是最优的，即它不能保证J(a)将取得最小值，也未实现观测矩阵的优化。若按照式(11)设计新观测向量每一步都可以保证J(a)最小，完成了观测矩阵优化。

经过2.1节的分析可知，若能确定每步观测使用的子矩阵A，则可根据式(11)计算得到新的观测向量，完成自适应观测。假设M₀、M_max分别为初始观测数和最大观测数，第i(i=0, 1, …, M_max－M₀)步观测所用观测矩阵为Φ^[i]，设第i次设计的新观测向量为φ_i=(a_i^T  b_i^T)∈R^1×N，其中, a_i∈R^L×1，b_i=0。刚开始观测时，为了保证初始估计的支撑集的可信度，应当预先分配适量随机观测向量作为初始观测矩阵，一般要求M₀>2K。在获得初始观测值后，利用传统CS重构算法得到估计支撑集${\mathit{\tilde {\Lambda}} ^{\left[0 \right]}} $，然后根据式(11)计算新的观测向量。新观测向量观测信号可获得新观测值，新观测向量与原观测矩阵组合成新的观测矩阵，新观测值与原观测值向量组成新的观测值向量，继而可通过传统CS重构方法获得估计支撑集。重复上述步骤，可完成自适应观测。本文所提自适应观测过程主要流程如下：

输入 初始观测矩阵Φ^[0](已经归一化)，初始观测值y^[0]，总观测数M_max；

输出 输出估计信号${\mathit{\boldsymbol{\tilde x}}^{\left[i \right]}} $，估计支撑集${\mathit{\tilde {\Lambda}} ^{\left[i \right]}} $。

初始化 步数i=0。

1) 利用传统CS恢复算法得到信号的估计${\mathit{\boldsymbol{\tilde x}}^{\left[i \right]}} $及支撑集估计${\mathit{\tilde {\Lambda}} ^{\left[i \right]}} $。

2) 获得子矩阵${\mathit{\boldsymbol{A}}^{\left[i \right]}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varLambda} }}}^{\left[i \right]}}}^{\left[i \right]} $。

3) 按照式(15)得到a_i，设置b_i=0，得到新观测向量φ_i=(a_i^Tb_i^T)，更新观测矩阵Φ^[i+1]=[Φ^[i]  φ_i]^T。

4) 观测信号：y_i+1=φ_i^Tx+w_i+1，w_i+1~N(0, σ_w²)为高斯观测噪声，更新观测值向量y^[i+1]=(y^[i]  y_i+1)^T。

5) 回到步骤1)，i=i+1，继续迭代，直到i=M_max－M₀。

上述机制的计算复杂度主要集中在获取估计支撑集和特征值分解，参与特征值分解的矩阵维度在K×K，这远低于贝叶斯方法求逆的矩阵维度N×N，即本文算法运算较之更快。又因为$ K \ll N$，复杂度可忽略不计，采用贪婪算法获得估计支撑集的复杂度一般在O(KM_maxN)，因为每一步观测都要运行贪婪算法，那么算法复杂度为O(KM₀N+K(M₀+1)N+…+KM_maxN)，显然高于贪婪算法，这是提高贪婪算法抗噪性能付出的代价。若减小自适应观测步数，在一定程度上，这种代价是可以接受的。

3 仿真实验与分析

为说明自适应观测和观测矩阵优化对传统CS恢复算法的抗噪性能的改善作用，仿真实验对SP算法及其相应自适应算法进行对比分析。为简化描述，将a设计为随机向量且采用SP恢复信号的自适应机制命名为随机自适应SP算法(Random Adaptive SP, R-ASP)，将a按式(15)设计且采用SP恢复信号的机制命名为优化的自适应SP算法(Optimized Adaptive SP, O-ASP)。为检验本文所提观测方案与其他类似方案的优劣，加入与BCS的性能对比，BCS初始观测数与O-ASP相同，其他参数参考文献[4]。

为评价本文所提自适应压缩感知算法的恢复性能，实验采用相对支撑集误差(Relative Support Set Error, RSSE)和归一化均方误差(Normalized Mean Square Error, NMSE)作为评价标准，它们可分别通过式(16)、(17)计算：

$ RSSE = 1-\left| {\mathit{\Lambda }-\cap \mathit{\tilde {\Lambda }}} \right|/K $

(16)

$ NMSE = 10\lg \left( {\left\| {\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{\tilde x}}} \right\|_2^2/\left\| \mathit{\boldsymbol{x}} \right\|_2^2} \right) $

(17)

其中: $\mathit{\tilde {\Lambda }} $、Λ分别为估计支撑集和真实支撑集；$\mathit{\boldsymbol{\tilde x}} $、x分别为估计信号和测试信号。随着观测信噪比的提高，Gram矩阵对角元素增大，J(a)并不能很好地描述误差性能，本文实验采用Gram矩阵的非对角元素(Off-diagonal Elements, OE)能量来描述，即：

$ {E_{{\rm{OE}}}} = \left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}-{\rm{diag}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)} \right\|_{\rm{F}}^2 $

(18)

其中diag(·)表示矩阵的对角元素构成的对角阵。

测试信号x为长为N的K-稀疏信号，且其非零项相互独立且服从均值为0、方差为1的高斯分布。观测矩阵元素相互独立且服从均值为0、方差为1的高斯分布并对其行向量归一化，那么总观测能量为M_max。定义观测信噪比为：

$ SNR = 10\lg \left( {\left\| \mathit{\boldsymbol{y}} \right\|_2^2/\left( {{M_{\max }}\sigma _\mathit{\boldsymbol{w}}^2} \right)} \right) $

(19)

其中y表示观测值向量；σ_w²表示高斯观测噪声的方差。观测信噪比增益通过式(20)计算：

$ {G_{{\rm{SNR}}}} = 10\lg \left( {\left\| {{\mathit{\boldsymbol{y}}_{{\rm{ad}}}}} \right\|_2^2/\left\| {{\mathit{\boldsymbol{y}}_{{\rm{nad}}}}} \right\|_2^2} \right) $

(20)

其中，y_nad、y_ad分别表示非自适应观测和自适应观测所得观测值向量。对于非自适应算法有y_ad=y_nad，则G_SNR=0。各实验分别进行500次蒙特卡洛仿真。

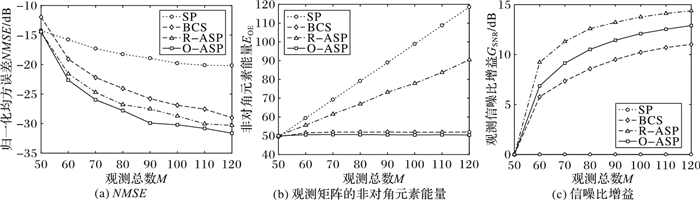
图 1(a)为不同算法重构NMSE随观测总数变化曲线；图 1(b)为随机观测矩阵和自适应观测矩阵(采用SP估计支撑集)非对角元素的能量E_OE随观测总数变化曲线; 图 1(c)为各算法信噪比增益G_SNR与观测总数的关系。图 1中，测试信号长度N=256，稀疏度K=5，自适应算法的初始观测数M₀=50，信噪比SNR=10 dB。

从图 1(a)易知，自适应观测对传统CS恢复算法的重构NMSE改善在10 dB以上，并且随着观测数增多改善越明显；R-ASP、O-ASP算法的重构NMSE低于BCS；O-ASP性能优于R-ASP，说明优化观测矩阵的策略是有效的。从图 1(b)可以看出，非自适应的随机观测和采用随机方式设计新观测向量的自适应观测的非对角元素能量都随着观测数增多而增大，而采用优化观测向量的BCS和O-ASP却几乎保持不变，并且O-ASP的非对角元素能量低于BCS，这是因为BCS设计新观测向量并未考虑观测矩阵的优化。从图 1(c)可知，自适应算法R-ASP、O-ASP和BCS的信噪比增益逐渐增大，而未实现自适应观测的SP算法没有信噪比增益；O-ASP的信噪比增益低于R-ASP而高于BCS，因为考虑了观测矩阵优化，O-ASP的重构性能仍优于R-ASP；因为BCS每一步的观测能量分配的位置一般多于K个，使其观测信噪比增益低于R-ASP和O-ASP。

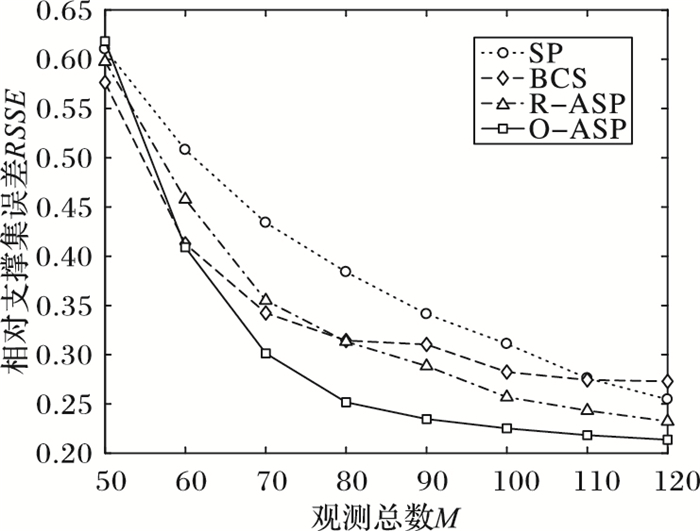
图 2为不同算法的RSSE与观测数的变化趋势，其中测试信号长度N=256，稀疏度K=15，自适应算法的初始观测数M₀=50，信噪比SNR=10 dB。由图 2可以发现，自适应算法BCS、R-ASP、O-ASP比非自适应算法SP具有更小的RSSE，当观测数较少时(M < 60)，BCS的RSSE相对最小，但误差仍较大，而随着观测数增多，O-ASP性能则优于BCS，且RSSE较小。而未采用观测矩阵优化的R-ASP直到M>80时RSSE才低于BCS，这进一步说明在自适应观测过程中考虑观测矩阵优化的策略是有效的。

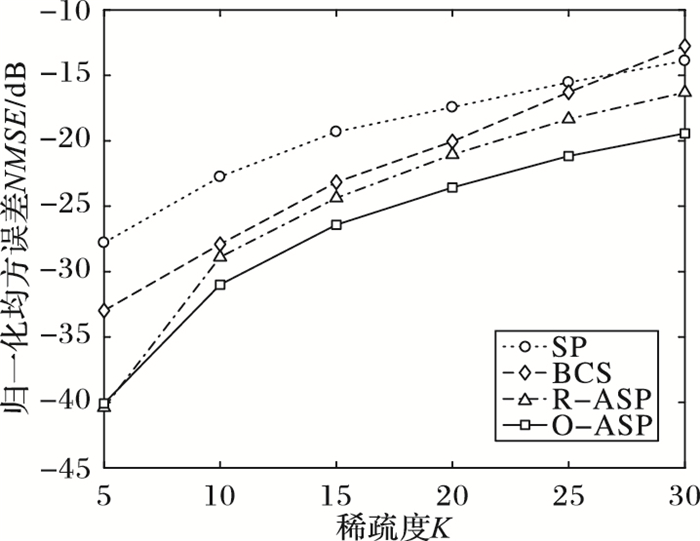
图 3为不同算法重构NMSE与稀疏度的关系，其中测试信号长度N=256，自适应算法的初始观测数M₀=70，总观测数M_max=128，信噪比SNR=15 dB。由图 3可知:随着稀疏度增大，各算法重构NMSE均增大，自适应算法BCS、R-ASP、O-ASP的NMSE一般低于SP; 但BCS随着K增大性能迅速恶化，甚至差于SP(当K>27)，R-ASP和O-ASP仍然具有最小的NMSE，而O-ASP的NMSE始终低于R-ASP，说明观测矩阵优化策略对恢复大稀疏度的信号具有优势。

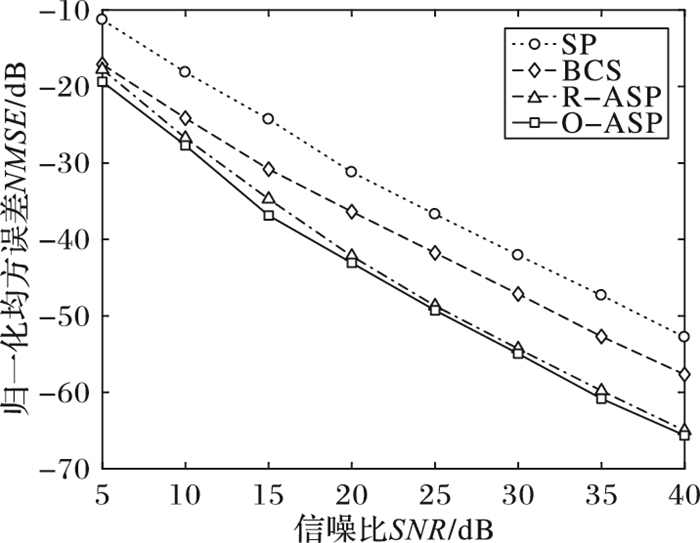
图 4为不同算法重构NMSE随信噪比变化曲线，其中测试信号长度N=256，稀疏度K=5，自适应算法的初始观测数M₀=50，总观测数M_max=80。

由图 4可知，R-ASP、O-ASP可改善SP重构NMSE达10 dB以上，并且随着信噪比增大，改善效果越明显，这验证了自适应观测对恢复性能的增益；O-ASP具有比R-ASP更低重构NMSE，表明观测矩阵优化对恢复性能的增益；并且，O-ASP的重构NMSE比BCS低至少5 dB(当SNR≥15 dB)，这是因为O-ASP每次观测都将能量集中在K个位置，而BCS的能量分配位置一般多于K个，故而O-ASP对观测信噪比的增益更高，使它们的抗噪性能优于BCS。

4 结语

本文结合自适应观测和观测矩阵优化的思想，提出一种自适应观测机制，在实现自适应观测的同时，也使观测矩阵得到优化。O-ASP的良好性能建立在估计支撑集的正确度上，如果估计支撑集不够准确(如观测数过少、信噪比过低等)，则使O-ASP恢复性能不及BCS；如果估计支撑集足够准确，则仅需要少量观测步骤就可恢复信号，并且恢复效果优于BCS。O-ASP综合利用了自适应观测和观测矩阵优化的优势，重构效果始终优于未采用自适应观测的SP和未采用观测矩阵优化的R-ASP。本文所提自适应观测机制因为每一步都需要传统CS恢复算法获得估计支撑集，需要更多的重构时间。此外，恢复信号要求预先设置观测总数，这不利于自适应观测。下一步工作将考虑如何以更低的复杂度获取较为准确的估计支撑集，以及如何自适应确定恢复信号所需的观测总数或确定停止观测条件。