2. 河南理工大学 物理与电子信息工程学院, 河南 焦作 454003
2. School of Physics and Electronic Information Engineering, Henan Polytechnic University, Jiaozuo Henan 454003, China
分布式多输入多输出(Distributed Multiple Input Multiple Output, D-MIMO)系统因其能够通过缩短收发距离提高数据速率, 减小发射功率,受到学术界和产业界的广泛关注[1-3]。在D-MIMO系统中,配置大规模天线的基站(Base Station, BS)与空间独立分布的多天线接入端口(Access Port, AP)通信。因此,BS与APs的链路受小尺度和大尺度衰落的影响,使得D-MIMO系统的性能分析更具挑战性[3]。另外,目前大多文献主要基于二维(Two-Dimensional, 2D)信道模型进行研究,但2D信道模型只考虑天线水平辐射增益的影响,忽略了垂直辐射增益的影响。为了使信道模型更加符合实际,提出了三维(Three-Dimensional, 3D) MIMO信道模型。对于3D-MIMO信道,天线下倾角3D模型是最普遍的模型,该模型被广泛应用于雷达和射频通信系统[4-5],并被第三代合作伙伴计划(the third Generation Partnership Project, 3GPP)采纳为LTE-Advanced (LTE-A)的无线通信标准[7]。然而,针对复合衰落信道下的3D D-MIMO系统性能的研究仍处于初始阶段。因此,本文研究基于K复合衰落信道的3D D-MIMO系统和速率的性能。
和速率作为性能的关键指标,被用来分析MIMO系统的性能[5, 7-12]。在文献[7]中,基于高斯-埃尔米特多项式,推导给出了瑞利/对数正态(Rayleigh/Lognormal, RLN)复合衰落信道场景下点对点MIMO系统的近似和速率闭式表达式。文献[8]基于Nakagami-m/对数正态(Nakagami-m/Lognormal, NLN)复合衰落信道,推导给出集中式MIMO和D-MIMO系统的和速率上下界的闭式表达式。运用随机矩阵理论,文献[5]推导出RLN复合衰落信道下迫零(Zero-Forcing, ZF)接收的3D MIMO系统和速率的闭式上界表达式,所得上界同时考虑小尺度衰落、大尺度衰落以及3D天线的辐射损耗。同时考虑水平和垂直增益,文献[9]提出一种联合有限反馈预编码方案。文献[10]基于K复合衰落信道,推导出3D多用户MIMO系统和速率的闭式下界,并进一步研究了下倾角对3D MIMO系统的性能影响。针对高楼覆盖场景,文献[11]研究基于线性最小均方误差(Minimum Mean Square Error, MMSE)检测方案下3D MIMO系统和速率性能,推导出系统和速率闭式表达式。然而,由于对数正态分布的存在,使得信息输出信噪比不存在闭式表达式。为了避免这个问题,文献[10, 12]用伽马分布近似对数正态分布,分析分布式MIMO和多用户MIMO和速率性能。上述所得模型,即K复合衰落,将是本文的参考模型。
鉴于上述分析,本文研究在K复合衰落信道下的3D D-MIMO系统性能,推导出D-MIMO系统ZF接收和速率上界的闭式表达式。所得和速率上界考虑AP分布和BS天线下倾角对系统性能的影响。基于所得闭式表达式,分析3D D-MIMO系统和速率渐进性能,推导出高信噪比条件下的近似表达式。最后,针对大规模天线配置下D-MIMO系统渐进性能进行分析。
1 3D-MIMO衰落信道模型和用户分布 1.1 3D MIMO衰落信道模型本文考虑单小区上行3D D-MIMO系统,每个小区分为三个扇区,每个扇区的BS配置有Nr个接收天线,K个AP,每个AP有Nt个发射天线(Nr≥KNt)。假设所有AP未知信道状态信息(Channel State Information, CSI),BS获知完备的CSI。因此,最佳的传输方案是全部用户等功率(pu)发送信息,根据以上所述,BS的接收信号向量y∈CNr×1[10]如下:
| $\mathit{\boldsymbol{y}} = \sqrt {\frac{{{p_u}}}{{K{N_t}}}} \mathit{\boldsymbol{Gx}}{\rm{ + }}\mathit{\boldsymbol{n}}$ | (1) |
其中:G∈CNr×KNt表示所在BS与所有AP之间的信道矩阵;gnk=[G]nk是BS的第n个天线与第k个AP之间的信道系数;x∈CKNt×1是K个AP的发送信号向量;n∈CNr×1是零均值、单位协方差的加性高斯白噪声(Addition White Gaussian Noise, AWGN), n~CN(0, INr)。
信道矩阵G包括小尺度和大尺度衰落,其表达式[12]为:
| $\mathit{\boldsymbol{G}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{\frac{1}{2}}}$ | (2) |
其中:H∈CNr×KNt表示瑞利衰落,其元素为CN(0, 1);对角矩阵Ω∈CKNt×KNt表示大尺度衰落,其表达式为Ω=diag{Ωk}k=1K=diag{ξka(Δφk, Δθk)dmvINt}k=1K(k=1, 2,…, K),其中dk表示BS与第k个AP的距离,v∈[2, 8]是路径损耗指数[13]。相应地,阴影衰落考虑伽马分布,ξk的概率密度函数(Probability Density Function, PDF)[3]为:
| $p\left( {{\xi _k}} \right) = \frac{{s_k^{{s_k}}\xi _k^{{s_k} - 1}}}{{\Gamma \left( {{s_k}} \right)m_k^{{s_k}}}}{\rm{exp}}\left( { - \frac{{{s_k}{\xi _k}}}{{{m_k}}}} \right),{\xi _k},{s_k},{m_k} \ge 0$ | (3) |
其中:sk和mk分别是伽马分布的形状和尺度参数[14]。
对于3D天线模型,下倾角模型被广泛应用于无线通信标准中,如LTE-A[6]。系数a(Δφk, Δθk)是BS 3D天线的辐射增益,由水平方位角和垂直俯仰角决定。(xBS, yBS, zBS)和(xk, yk, zk)分别是BS与第k个用户的坐标,第k个AP与BS的x轴坐标差值即Δxk=xk-xBS。同理,可获得Δyk和Δzk。
则相应的水平方位角和垂直俯仰角[5]为:
| $\Delta {\phi _k} = {\rm{atan}}2\left( {\Delta x,\Delta y} \right) - {\alpha _{{\rm{orn}}}}$ | (4) |
| $\Delta {\theta _k} = {\rm{atan}}2\left( {\Delta z,\sqrt {{{\left( {\Delta x} \right)}^2} + {{\left( {\Delta y} \right)}^2}} } \right) - {\beta _{{\rm{tilt}}}}$ | (5) |
其中:αorn为固定初始方向角,βtilt∈[-90°, 90°]表示天线下倾角。
因此,天线增益a(Δφk, Δθk)可以表示如下(所有a值用分贝表示)[6]:
| $a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right) = {a_h}\left( {\Delta {\phi _k}} \right) + {a_v}\left( {\Delta {\theta _k}} \right)$ | (6) |
| ${a_{\rm{h}}}\left( {\Delta {\phi _k}} \right) = - {\rm{min}}\left\{ {12{{\left( {\Delta {\phi _k}/{\phi _{{\rm{3dB}}}}} \right)}^2},SL{L_{\rm{h}}}} \right\} + {A_{\rm{m}}}$ | (7) |
| ${a_{\rm{v}}}\left( {\Delta {\theta _k}} \right) = {\rm{max}}\left\{ { - 12{{\left( {\Delta {\theta _k}/{\theta _{{\rm{3dB}}}}} \right)}^2},SL{L_{\rm{v}}}} \right\}$ | (8) |
其中:ah和av分别表示天线的水平和垂直增益;φ3dB和θ3dB分别表示水平和垂直半功率波束宽度(Half-Power BeamWidth, HPBW);SLLh和SLLv分别表示水平和垂直旁瓣电平;最后,Am表示最大天线增益。此外,第k个用户与BS之间的距离dk可表示为:
| ${d_k} = \sqrt {{{\left( {\Delta x} \right)}^2} + {{\left( {\Delta y} \right)}^2} + {{\left( {\Delta z} \right)}^2}} $ | (9) |
综上所述,大尺度衰落系数[5]可表示为:
| ${\mathit{\Omega }_k} = {\xi _k}{10^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}d_k^{ - v}$ | (10) |
本节讨论AP的分布。为了便于分析,假设小区近似为圆形,AP独立且均匀地分布在R1≥R0的环形区域内。因此,用户极坐标(x, α)形式的概率密度函数[10]为:
| $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{2x}}{{R_1^2 - R_0^2}},} & {{R_0} \le x \le {R_1}}\\ {0,} & {其他} \end{array}} \right.$ | (11) |
| $f\left( \alpha \right) = 1/\left( {2{\rm{ \mathsf{ π} }}} \right),0 \le \alpha \le 2{\rm{ \mathsf{ π} }}$ | (12) |
其中:R1是小区的半径,R0是BS与AP的最小距离。
2 可达和速率及上界本章分析基于K复合衰落信道的3D D-MIMO系统的上界。首先,给出基于ZF接收的3D D-MIMO系统的可达和速率性能。基于信号与干扰加噪声比(Signal Interference Plus Noise Ratio, SINR)的统计特征, 推导出在K复合衰落信道下,ZF接收的3D D-MIMO系统的两种可达和速率上界的闭式表达式。
2.1 3D D-MIMO系统的可达和速率如第1章的讨论,所有AP未知CSI,BS获知完备的CSI。通过线性检测器,BS检测后信息为:
| $\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{y}}$ | (13) |
将式(1)代入式(13),检测信息可表示为:
| $\mathit{\boldsymbol{r}} = \sqrt {\frac{{{p_u}}}{{K{N_t}}}} {\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{Gx}} + {\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{n}}$ | (14) |
因此,由第k个AP发送到BS的接收信号为:
| ${\gamma _k} = \sqrt {\frac{{{p_u}}}{{K{N_t}}}} \mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_k}{\mathit{\boldsymbol{x}}_k} + \sum\limits_{i = 1,i \ne k}^{K{N_t}} {\sqrt {\frac{{{p_u}}}{{K{N_t}}}} \mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{x}}_i}} + \mathit{\boldsymbol{a}}_k^{\rm{H}}\mathit{\boldsymbol{n}}$ | (15) |
其中,ak和gk分别表示检测矩阵A和信道矩阵G的第k列元素,因此第k个AP的SINR为:
| ${\gamma _k} = \frac{{\frac{{{p_u}}}{{K{N_t}}}{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_k}} \right|}^2}}}{{\frac{{{p_u}}}{{K{N_t}}}\sum\limits_{i = 1,i \ne k}^K {{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_i}} \right|}^2} + {{\left\| {{\mathit{\boldsymbol{a}}_k}} \right\|}^2}} }}$ | (16) |
本文采用ZF检测器,AH=(GHG)-1GH[15],因此系统的SINR式γkZF为:
| $\gamma _k^{{\rm{ZF}}} = \frac{{{p_u}}}{{K{N_t}{{\left[ {{{\left( {{\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{G}}} \right)}^{ - 1}}} \right]}_{kk}}}} = \frac{{{p_u}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}}}{{K{N_t}{{\left[ {{{\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)}^{ - 1}}} \right]}_{kk}}}}$ | (17) |
根据式(17)可知,可达和速率是通过所有独立AP速率之和获得:
| ${{\mathscr{R}}^{{\rm{ZF}}}} = \sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {1 + {\gamma _k}} \right)} \right]} $ | (18) |
其中期望操作针对小尺度衰落H和大尺度衰落Ω(阴影衰落和路径损耗)。
2.2 和速率的闭式上界利用文献[16]和[17]的相关结论,推导出K复合衰落信道场景下3D D-MIMO系统和速率上界的闭式表达式,具体由以下定理给出。
定理 1 对于K复合衰落信道,基于ZF接收的3D D-MIMO系统可达和速率上界通过
| $\begin{array}{l} {{\mathscr{R}}_1^{{\rm{ZF}}}} = \\ \quad K{N_t}{\mathop{\rm l}\nolimits} {\rm{b}}\left( {\frac{1}{{{N_r} - K{N_t}}} + \frac{{2\alpha {p_u}}}{{{{\left( {K{N_t}} \right)}^2}}}\sum\limits_{k = 1}^{K{N_t}} {\left( {{m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right)} } \right) + \\ \quad \frac{{K{N_t}}}{{{\rm{ln}}2}}\psi \left( {{N_r} - K{N_t} + 1} \right) \end{array}$ | (19) |
其中:
证明 为便于分析,令W=HHH。将式(17)代入式(18),可得出:
| $\begin{array}{l} {\mathscr{R}^{_{{\rm{ZF}}}}} = \sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}(1 + \frac{{{p_u}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}}}{{K{N_t}{{\left[ {{{\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)}^{ - 1}}} \right]}_{kk}}}})} \right]} = \\ \;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}(1 + \frac{{{p_u}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}}}{{K{N_t}{{\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]}_{kk}}}})} \right]} = \\ \;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}({{\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]}_{kk}} + \frac{{{p_u}}}{{K{N_t}}}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}) - {\mathop{\rm l}\nolimits} {\rm{b}}\left( {{{\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]}_{kk}}} \right)} \right] = } \\ \;\;\;\;\;\;\underbrace {\sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}({{\left[ {{{\bf{W}}^{ - 1}}} \right]}_{kk}} + \frac{{{p_u}}}{{K{N_t}}}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}})} \right]} }_c - \\ \;\;\;\;\;\;\;\;\underbrace {\sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {{{\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]}_{kk}}} \right)} \right]} }_d \end{array}$ | (20) |
鉴于文献[16],式(20)的第一项的上界可表示为:
| $\begin{array}{l} c\mathop \le \limits^{\left( a \right)} \\ K{N_t}E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\frac{1}{{K{N_t}}}\left( {\sum\limits_{k = 1}^{K{N_t}} {\left( {{{\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]}_{kk}}} \right) + \frac{1}{{{{\left( {K{N_t}} \right)}^2}}}\sum\limits_{k = 1}^{K{N_t}} {\left( {{p_u}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}} \right)} } } \right)} \right] = \\ K{N_t}E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {\frac{1}{{K{N_t}}}{\rm{tr}}\left( {{\mathit{\boldsymbol{W}}^{ - 1}}} \right) + \frac{1}{{{{\left( {K{N_t}} \right)}^2}}}\sum\limits_{k = 1}^{K{N_t}} {\left( {{p_u}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}} \right)} } \right)} \right]\;\mathop \le \limits^{\left( b \right)} \\ K{N_t}\left( {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {\frac{1}{{K{N_t}}}E\left[ {{\rm{tr}}\left( {{\mathit{\boldsymbol{W}}^{ - 1}}} \right)} \right] + \frac{1}{{{{\left( {K{N_t}} \right)}^2}}}{p_u}\sum\limits_{k = 1}^{K{N_t}} {E\left\{ {{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}} \right\}} } \right)} \right) = \\ K{N_t}\left( {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {E\left[ {{\lambda ^{ - 1}}} \right] + \frac{1}{{{{\left( {K{N_t}} \right)}^2}}}{p_u}\sum\limits_{k = 1}^{K{N_t}} {E\left\{ {{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}} \right\}} } \right)} \right) \end{array}$ | (21) |
其中:λ是矩阵H的无序特征值,(a)源于算数平均值和几何平均值之间的关系,(b)通过杰森不等式获得。
式(21)的第一项可通过文献[19]的结果简化为:
| $E\left\{ {\frac{1}{\lambda }} \right\} = \frac{1}{{{N_r} - K{N_t}}}$ | (22) |
由于阴影衰落、辐射增益、路径损耗相互独立,式(21)的最后一项可改写为:
| $\begin{array}{l} E\left\{ {{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}} \right\} = E\left\{ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_k}} \right\} = E\left( {{\xi _k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}d_k^{ - v}} \right) = \;\\ \underbrace {E\left( {{\xi _k}} \right)}_{①}\underbrace {E\left( {{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right)}_{②}\underbrace {E\left( {d_k^{ - v}} \right)}_{③} \end{array}$ | (23) |
| $\begin{array}{l} ① = \int_0^{ + \infty } {{\xi _k}p\left( {{\xi _k}} \right)} {\rm{d}}\left( {{\xi _k}} \right) = \\ \frac{{s_k^{{s_k}}}}{{\Gamma \left( {{s_k}} \right)m_k^{{s_k}}}} \times \int_0^{ + \infty } {\xi _k^{{s_k} - 1}{\xi _k}} {\rm{exp}}\left( { - \frac{{{s_k}{\xi _k}}}{{{m_k}}}} \right){\rm{d}}\left( {{\xi _k}} \right) \end{array}$ | (24) |
使用下面的积分恒等式和伽马函数的性质[19]:
| $\int_0^{ + \infty } {{x^{u - 1}}} {\rm{exp}}\left( { - \mu x} \right){\rm{d}}x = \frac{{\Gamma \left( u \right)}}{{{\mu ^u}}}$ | (25) |
| $\Gamma \left( {x + 1} \right) = x\Gamma \left( x \right)$ | (26) |
经过一些简化,式(24)的结果可以进一步简化为:
| $① = {m_k}$ | (27) |
对于②,结果如下:
| $② = {10^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}$ | (28) |
结合式(11)和期望的定义,③可以进一步表示为:
| $\begin{array}{l} ③ = \int_{{R_0}}^{{R_1}} {d_k^{ - v}p\left( {{d_k}} \right)} {\rm{d}}\left( {{d_k}} \right) = \frac{2}{{R_1^2 - R_2^2}}\int_{{R_0}}^R {d_k^{ - v + 1}} {\rm{d}}\left( {{d_k}} \right) = \\ \;\;\;\;\frac{{2\left( {R_1^{2 - v} - R_0^{2 - v}} \right)}}{{\left( {R_1^2 - R_0^2} \right)\left( {2 - v} \right)}} \end{array}$ | (29) |
代入式(27)、(28)和(29)到式(23),可获得大尺度衰落:
| $E\left\{ {{\mathit{\Omega }_k}} \right\} = 2{m_k}{10^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}\frac{{\left( {R_1^{2 - v} - R_0^{2 - v}} \right)}}{{\left( {R_1^2 - R_0^2} \right)\left( {2 - v} \right)}}$ | (30) |
因此,结合式(22)和式(30),可获得式(21)的最后结果:
| $\begin{array}{l} c = K{N_t}{\mathop{\rm l}\nolimits} {\rm{b}}\left( {\frac{1}{{{N_r} - K{N_t}}} + \frac{{{p_u}}}{{{{\left( {K{N_t}} \right)}^2}}}} \right. \times \\ \left. {\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} {\left( {{m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}\frac{{2\left( {R_1^{2 - v} - R_0^{2 - v}} \right)}}{{\left( {R_1^2 - R_0^2} \right)\left( {2 - v} \right)}}} \right)} } \right) \end{array}$ | (31) |
借助于以下关键矩阵性质[20]:
| ${\left[ {{\mathit{\boldsymbol{W}}^{ - 1}}} \right]_{kk}} = \frac{{{\rm{det}}({\mathit{\boldsymbol{W}}_{kk}})}}{{{\rm{det}}\left( \mathit{\boldsymbol{W}} \right)}} = \frac{{{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})}}{{{\rm{det}}\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)}}$ | (32) |
将式(32)代入式(20)的d可表示为:
| $\begin{array}{l} d = \sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})} \right) - {\mathop{\rm l}\nolimits} {\rm{b}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)} \right)} \right]} {\rm{ = }}\\ \;\quad \sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})} \right)} \right] - K{N_t}E\left[ {{\mathop{\rm l}\nolimits} {\rm{b}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)} \right)} \right]} {\rm{ = }}\\ \;\quad \sum\limits_{k = 1}^{K{N_t}} {\frac{1}{{{\rm{ln2}}}}E\left[ {{\rm{ln}}\left( {{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})} \right)} \right] - } \\ \;\quad \frac{{K{N_t}}}{{\ln 2}}E\left[ {{\rm{ln}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)} \right)} \right] \end{array}$ | (33) |
根据文献[16],可知:
| $E\left[ {{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})} \right] = \frac{{{N_r}!}}{{({N_r} - K{N_t})!}}$ | (34) |
| $E\left[ {{\rm{ln}}\left( {{\rm{det}}(\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}_k})} \right)} \right] = \sum\limits_{m = 0}^{K{N_t} - 1} {\psi ({N_r} - m)} $ | (35) |
经过一些运算,结合式(31)、(33)、(34)和式(35),可得出式(19)的结论。
由定理1可知,和速率随着参数pu、mk、a(Δφk, Δθk)和R0的增加而增加,随着小区较大半径R1的增加而减少。此外,还可以观察到,增加更多的发射天线对于和速率并不总是有益的。
为了揭示系统参数对和速率的影响,接下来的推论对高信噪比条件下的和速率进行渐进性分析。
推论 1 对于高信噪比,和速率上界可进一步表述为:
| $\mathscr{R}{{_{1}^{\text{ZF}}}^{\infty }}=K{{N}_{t}}1\text{b}\left( \frac{{{p}_{u}}}{K{{N}_{t}}} \right)+K{{N}_{t}}1\text{b}\left( \frac{2\alpha }{K{{N}_{t}}}\sum\limits_{k=1}^{K{{N}_{t}}}{{{m}_{k}}{{10}^{\frac{a\left( \Delta {{\phi }_{k}},\Delta {{\theta }_{k}} \right)}{10}}}} \right)$ | (36) |
证明 对于高pu值,式(19)中对数函数的常数项可忽略不计。用定理1相似的方法可完成证明。
对于推论1,可以观察到,和速率随着天线的最小值的增大而增大,此结果与文献[16]的结果相一致。接下来,用不同的方法推导出相似的上界,以下定理给出了关键的结果。
定理 2 在K复合衰落信道情况下,基于ZF接收的3D D-MIMO系统可达和速率的上界可表示为
| $\begin{array}{l} \mathscr{R}_2^{{\rm{ZF}}} = \sum\limits_{k = 1}^{K{N_t}} {\left( {1{\rm{b}}\left( {\frac{{{N_r}!}}{{\left( {{N_r} - K{N_t} + 1} \right)!}} + \frac{{2\alpha {p_u}{N_r}!}}{{K{N_t}\left( {{N_r} - K{N_t}} \right)!}} \times } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left. {\left( {{m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right)} \right)} \right) - \frac{{K{N_t}}}{{{\rm{ln}}2}}\sum\limits_{m = 1}^{K{N_t} - 1} {\psi \left( {{N_r} + 1 - m} \right)} \end{array}$ | (37) |
证明 结合式(17)和式(18),可得出表达式:
| $\begin{array}{l} { \mathscr{R}^{{\rm{ZF}}}} = \sum\limits_{k = 1}^{K{N_t}} {E\left[ {1{\rm{b}}\left( {1 + \frac{{\frac{{{p_u}}}{{K{N_t}}}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}{\rm{det}}\left( \mathit{\boldsymbol{W}} \right)}}{{{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right)}}} \right)} \right] = } \\ \;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} {E\left[ {1{\rm{b}}\left( {\frac{{{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right) + \frac{{{p_u}}}{{K{N_t}}}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}{\rm{det}}\left( \mathit{\boldsymbol{W}} \right)}}{{\det \left( {{\mathit{\boldsymbol{W}}_{kk}}} \right)}}} \right)} \right]} = \\ \;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} E \left[ {1{\rm{b}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right) + \frac{{{p_u}}}{{K{N_t}}}{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}{\rm{det}}\left( \mathit{\boldsymbol{W}} \right)} \right)} \right. - \\ \;\;\;\;\;\;\;\;\;\left. {1{\rm{b}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right)} \right)} \right] = \\ \;\;\;\;\;\;\sum\limits_{k = 1}^{K{N_t}} {1{\rm{b}}\left[ {E\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right) + \frac{{{p_u}}}{{K{N_t}}}E\left[ {{{\left[ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right]}_{kk}}{\rm{det}}\left( \mathit{\boldsymbol{W}} \right)} \right]} \right)} \right]} - \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{\rm{ln}}2}}\sum\limits_{k = 1}^{K{N_t}} {E\left[ {{\rm{ln}}\left( {{\rm{det}}\left( {{\mathit{\boldsymbol{W}}_{kk}}} \right)} \right)} \right]} \end{array}$ | (38) |
利用式(30)、(34)和式(35)的结论,借助杰森不等式,可得出式(37)的结果。
如定理1所讨论,上界
同理,为了进一步揭示系统和衰落参数对性能的影响,接下来将对定理2的高信噪比渐进性能进行分析。
推论 2 高信噪比下,系统和速率上界趋近于:
| $\begin{align} & \mathscr{R}{{_{1}^{\text{ZF}}}^{\infty }}=K{{N}_{t}}1\text{b}\left( \frac{{{p}_{u}}}{K{{N}_{t}}} \right)+\frac{K{{N}_{t}}}{\text{ln}2}\psi \left( {{N}_{r}}-K{{N}_{t}}+1 \right)+ \\ & \ \ \ \ \ \ \ \ \ \sum\limits_{k=1}^{K{{N}_{t}}}{1\text{b}\left( 2\alpha {{m}_{k}}{{10}^{\frac{a\left( \Delta {{\phi }_{k}},\Delta {{\theta }_{k}} \right)}{10}}} \right)} \\ \end{align}$ | (39) |
证明 对于高信噪比(pu→∞), 式(38)对数中的主项为
推论2解释了系统参数和衰落参数对性能的影响。由推论2可知,和速率渐近线性能随着信噪比(pu)和衰落参数(mk)增加呈对数增加,该结论与文献[10]的结果一致。
2.3 大规模MIMO系统的渐进分析近年来,大规模MIMO技术由于具有高频谱效率和能量效率等优势,被认为是未来第五代移动通信的突破性技术之一[15, 24-26]。然而,在大规模系统中,关于3D D-MIMO系统对和速率性能影响的研究还很少。鉴于此,本文对大规模系统的渐进性能进行分析,并给出ZF接收的3D D-MIMO系统和速率的闭式表达式。
推论 3 对于大规模配置(Nr→∞),第一种上界
| $\begin{array}{l} \mathscr{R}_1^{{\rm{ZF}}} = K{N_t}1{\rm{b}}\left( {\frac{{{p_u}}}{{K{N_t}}}} \right) + K{N_t}1{\rm{b}}\left( {\frac{{2\alpha }}{{K{N_t}}}} \right.\left. {\sum\limits_{k = 1}^{K{N_t}} {\left( {{m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right)} } \right) + \\ \;\;\;\;\;\;\;\;\;K{N_t}1{\rm{b}}\left( {{N_r}} \right) \end{array}$ | (40) |
证明 当式(19)中的Nr趋于无穷大时,根据以下等式[31]
| $\psi \left( x \right) \approx {\rm{ln}}\left( x \right),\;x \to \infty $ | (41) |
利用与定理1的方法,经过一些简化,可得出式(40)的结果。
推论3的结果显示和速率随着发射功率pu和BS天线个数Nr的增加呈对数增加。接下来,当BS天线个数趋于无穷时,对
推论 4 对于大规模配置(Nr→∞),第二种上界
| $\begin{array}{l} \mathscr{R}_2^{{\rm{ZF}}} = K{N_t}1{\rm{b}}\left( {\frac{{{p_u}}}{{K{N_t}}}} \right) + \sum\limits_{k = 1}^{K{N_t}} {1{\rm{b}}\left( {2\alpha {m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right) + } \\ \;\;\;\;\;\;\;\;\;\;K{N_t}1{\rm{b}}\left( {{N_r}} \right) \end{array}$ | (42) |
证明 利用式(40),式(31)可进一步表示为:
| $\begin{array}{l} \mathscr{R}_2^{{\rm{ZF}}} = K{N_t}1{\rm{b}}\left( {\frac{{{p_u}}}{{K{N_t}}}} \right) + \sum\limits_{k = 1}^{K{N_t}} {1{\rm{b}}\left( {2\alpha {m_k}{{10}^{\frac{{a\left( {\Delta {\phi _k},\Delta {\theta _k}} \right)}}{{10}}}}} \right)} + \\ \quad \quad K{N_t}1{\rm{b}}\left( {\frac{{{N_r}!}}{{\left( {{N_r} - K{N_t}} \right)!}}} \right) - K{N_t}\left( {K{N_t} - 1} \right)1{\rm{b}}\left( {{N_r}} \right) \end{array}$ | (43) |
利用以下等式[18]:
| ${\rm{ln}}\;x! \approx x\;{\rm{ln}}\;x - x,\;x \to \infty $ | (44) |
经过一些代数运算,可得出式(42)的结果。
从推论3和推论4可以得出,当BS天线个数增大时,第二种上界趋于第一种上界。此外,在大规模天线配置下,小尺度衰落影响可以忽略,这与文献[5]和文献[17]的结果相一致。最后,可以观察到,增大发射功率和BS天线个数对系统性能总是有益的。
3 仿真结果本章通过仿真验证2.2节和2.3节分析的正确性。对于多径、阴影信道和AP分布,通过100000次随机生成、瑞利、伽马随机变量以及AP的随机位置,并通过式(18)获得系统的蒙特卡洛和速率。假设天线倾角正方向向下,在没有特殊说明的情况下,系统和3D MIMO仿真参数如表 1所示。
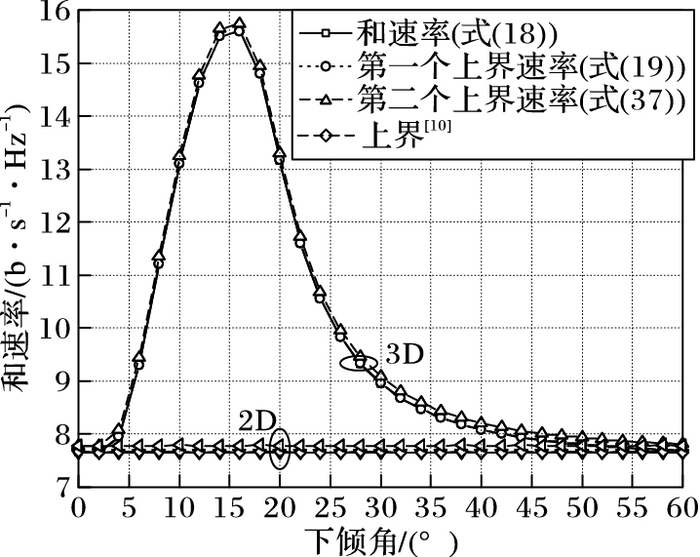
图 1仿真验证了式(19)中的第一种上界,式(37)中的第二种上界和式(18) [10]中的蒙特卡洛仿真间的紧密性。由图 1可知,3D D-MIMO系统的和速率在临界角之前随着倾角的增加而增加,之后随着倾角的增大而减小。受天线垂直俯仰角的影响,3D D-MIMO系统的性能在天线倾角为5°~40°优于2D D-MIMO系统。从图 1还可以观察到,两种上界在整个倾角范围保持足够紧密,且第一种上界比第二种上界更加紧密。
|
图 1 天线倾角对和速率及其上界的影响(Nr=20, Nt=2, K=1) Figure 1 Antenna dip angle versus velocity and its upper bound (Nr=20, Nt=2, K=1) |
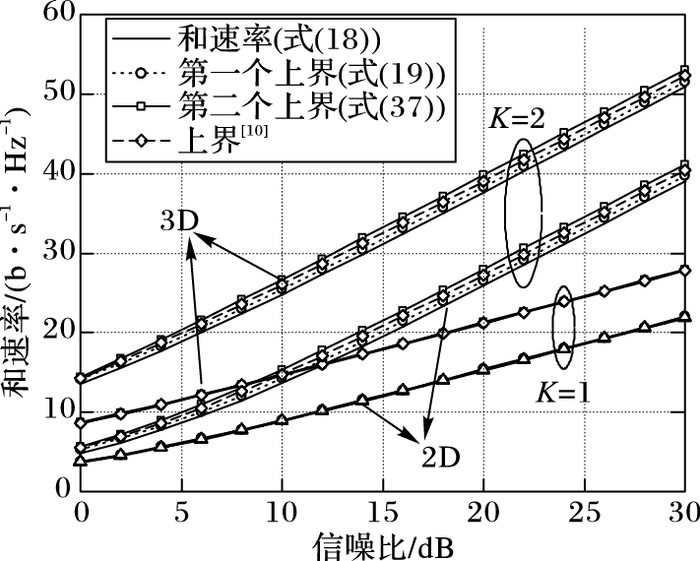
图 2仿真分析了式(19)中第一个上界、式(37)中第二个上界、文献[10]中式(18)上界以及蒙特卡洛仿真结果。本仿真考虑在不同数目AP的情况(K=1, 2)。
|
图 2 信噪比对和速率及其上界的影响(Nr=20, Nt=2, K=1, 2) Figure 2 Effect of SPNR on sum rate and its upper bound (Nr=20, Nt=2, K=1, 2) |
正如图 1所讨论,在整个信噪比范围,三种上界保持紧密,并且三个上界与蒙特考虑逼近程度依次为(逼近关系由紧至松):第一个上界、文献[10]的上界、第二种上界。在K=1时三个上界比K=2时逼近程度更好,其原因在于路径损耗和阴影衰落的差异。此外,在整个信噪比范围,本文给出的第一个上界要优于文献[10]的上界,而本文的第二个上界要次于文献[10]的结果。再者,由图 2还可以看出,随着信噪比的增加(K=2),三种上界的逼近程度逐渐变差。最后,可以得出,3D D-MIMO系统的性能在整个倾角范围优于2D D-MIMO系统的性能。
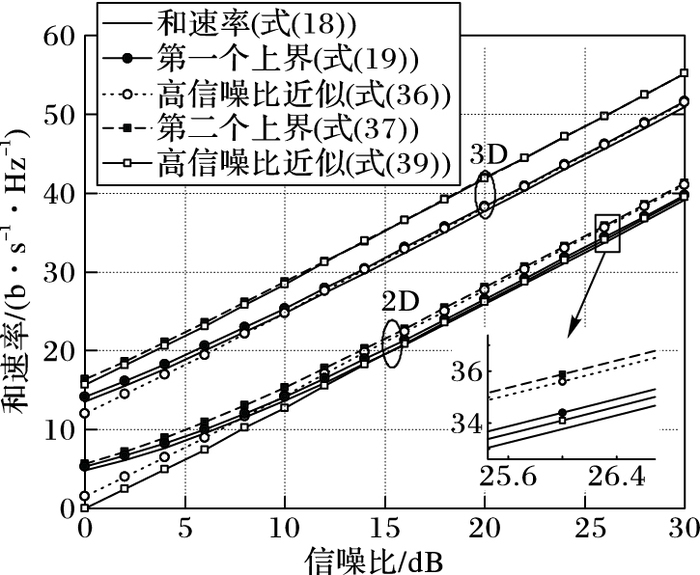
图 3仿真给出了理论分析、高信噪比近似以及蒙特卡洛性能关系图。由图 3可以看出,在高信噪比情况下,式(36)和(39)的渐进性能与式(19)和(37)充分一致。由此表明理论分析的正确性。此外,图 3还表明3D MIMO随着信噪比的增加趋近于上界的速度要快于2D MIMO系统,相似的结论在文献[27]中出现过。最后,由局部放大图可以看出,在高信噪比情况下,理论分析、高信噪比近似以及蒙特卡洛性能曲线充分一致。
|
图 3 和速率、上界与高信噪比近似关系(Nr=20, Nt=2, K=2) Figure 3 Simulation, upper bounds and high SNR approximations versus SNR |
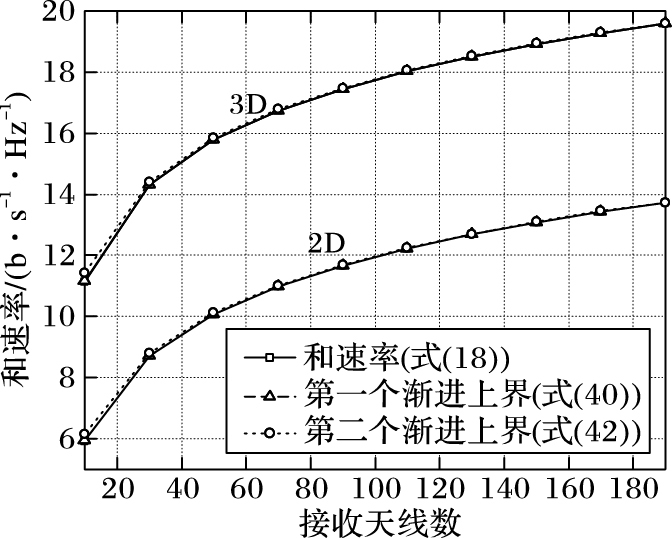
图 3显示不同的BS天线数对和速率性能以及式(39)和(41)中上界的影响。正如预期,和速率随BS天线个数Nr呈对数增长,验证了理论分析。此外,还可以得出,两种上界随着BS天线个数增多而变紧,且第一种上界比第二种上界更紧密。对于大规模接收天线Nr,所得上界与理论和速率相一致。最后,3D D-MIMO系统的和速率性能优于2D D-MIMO系统。
|
图 4 BS天线数对和速率及其上界的影响(Nt=2, K=1) Figure 4 Effects of base station antennas on sum rate and its upper bound (Nt=2, K=1) |
本文针对K复合衰落信道,基于ZF接收的3D D-MIMO系统可达和速率性能进行分析。首先推导出两种上界的闭式表达式,这两种表达式适用于任意天线数和信噪比。同时考虑3D MIMO和3D用户分布, 利用所得上界对大规模MIMO系统的新兴领域进行了详细的研究,并给出“大系统”极限的有利结果。总之,在BS配置更多天线的情况下,适当的天线下倾角和用户数才能获得最佳和速率。
| [1] | 彭文杰, 李岳衡, 薛团结, 等. 复合衰落信道下分布式MIMO系统中断概率及信道容量分析[J]. 通信学报, 2015, 36(2): 225-233. (PENG W J, LI Y H, XUE T J, et al. Outage probability and capacity analysis of distributed MIMO systems over a composite fading channel[J]. Journal on Communications, 2015, 36(2): 225-233.) |
| [2] | LI X, LI L, SU X, et al. Approximate capacity analysis for distributed MIMO system over generalized-K fading channels[C]//Proceedings of the 2015 IEEE Wireless Communications and Networking Conference. Piscataway, NJ:IEEE, 2015:235-240. |
| [3] | 李兴旺. 无线通信系统中的大规模MIMO关键理论及技术研究[D]. 北京: 北京邮电大学, 2015: 1-104. (LI X W. Research on key theory and technology of wireless massive MIMO system[D]. Beijing:Beijing University of Posts and Telecommunications, 2015:1-104.) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=kjzw201701018&dbname=CJFD&dbcode=CJFQ |
| [4] | VASILIADIS T G, DIMITRIOU A G, SERGIADIS G D. A novel technique for the approximation of 3-D antenna radiation patterns[J]. IEEE Transactions on Antennas & Propagation, 2005, 53(7): 2212-2219. |
| [5] | LI X, LI L, XIE L. Achievable sum rate analysis of ZF receivers in 3D MIMO systems[J]. KSⅡ Transactions on Internet & Information Systems, 2014, 8(4): 1368-1389. |
| [6] | 3GPP TR 38.873 V12.2.0, Study on 3D channel model for LTE[EB/OL].[2017-05-20].https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2574. |
| [7] | PARK M, CHAE C B, HEATH R W. Ergodic capacity of spatial multiplexing MIMO systems with ZF receivers for log-normal shadowing and Rayleigh fading channels[C]//Proceedings of the 18th International Symposium on Personal, Indoor and Mobile Radio Communications. Piscataway, NJ:IEEE, 2007:1-5. |
| [8] | ZHONG C, WONG K K, JIN S. Capacity bounds for MIMO Nakagami-m fading channels[J]. IEEE Transactions on Signal Processing, 2009, 57(57): 3613-3623. |
| [9] | 白帆, 李汀, 李飞, 等. 3D MIMO系统水平和垂直维联合与编码的研究[J]. 信号处理, 2016, 32(9): 1093-1100. (BAI F, LI T, LI F. Research on joint precoding of horizontal and vertical dimension in 3D MIMO system[J]. Journal of Signal Processing, 2016, 32(9): 1093-1100.) |
| [10] | 李兴旺, 艾晓宇, 张艳琴, 等. K复合衰落信道下3D多用户MIMO系统的性能分析[J]. 北京邮电大学学报, 2016, 39(5): 56-60. (LI X W, AI X Y, ZHANG Y Q, et al. Performance analysis of 3D MU-MIMO systems over K composite fading channels[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(5): 56-60.) |
| [11] | 谢玲. 3D MIMO关键传输技术的研究[D]. 北京: 北京邮电大学, 2015: 1-58. (XIE L. Research on key techniques of 3D MIMO[D]. Beijing:Beijing University of Posts and Telecommunications, 2015:1-58.) http://cdmd.cnki.com.cn/Article/CDMD-10013-1015584120.htm |
| [12] | 何杰, 肖琨. 基于独立同分布广义K信道的OSTBC-MIMO系统及性能[J]. 计算机应用, 2016, 36(9): 2390-2395. (HE J, XIAO K. Performance analysis of OSTBC-MIMO systems over i.n.i.d. generalized-K fading channels[J]. Journal of Computer Applications, 2016, 36(9): 2390-2395. DOI:10.11772/j.issn.1001-9081.2016.09.2390) |
| [13] | GOLDSMITH A. 无线通信[M]. 杨鸿文, 译. 北京: 人民邮电出版社, 2007: 23-47. (GOLDSMITH A. Wireless Communications[M]. YANG H W, translation. Beijing:Post & Telecom Press, 2007:23-47.) |
| [14] | KRISHNAMOORTHY K. Handbook of Statistical Distributions with Applications[EB/OL].[2016-11-10]. http://www.crcnetbase.com/doi/pdf/10.1201/b19191-1. |
| [15] | 李兴旺, 张辉, 王俊峰, 等. 5G大规模MIMO:理论、算法与关键技术[M]. 北京: 机械工业出版社, 2017: 97-113. (LI X W, ZHANG H, WANG J F, et al. 5G Massive MIMO:Theory, Algorithm, Key Technology[M]. Beijing: China Machine Press, 2017: 97-113.) |
| [16] | MATTHAIOU M, ZHONG C, RATNARAJAH T. Novel generic bounds on the sum rate of MIMO ZF receivers[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4341-4353. DOI:10.1109/TSP.2011.2157148 |
| [17] | MATTHAIOU M, ZHONG C, MCKAY M R, et al. Sum rate analysis of ZF receivers in distributed MIMO systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 180-191. DOI:10.1109/JSAC.2013.130207 |
| [18] | GRADSHTEUIN I S, RYZHIK I M, JEFFREY A, et al. Table of integrals, series, and products[EB/OL].[2016-11-10].http://tocs.ulb.tu-darmstadt.de/17898919.pdf. |
| [19] | LOZANO A, TULINO A M, VERDU S. Multiple-antenna capacity in the low-power regime[J]. IEEE Transactions on Information Theory, 2003, 49(10): 2527-2544. DOI:10.1109/TIT.2003.817429 |
| [20] | LI X, LI L, LING X, et al. Performance analysis of 3D massive MIMO cellular systems with collaborative base station[J]. International Journal of Antenna and Propagation, 2014, 61(14): 1-12. |
| [21] | GRANT A. Rayleigh fading multi-antenna channels[J]. EURASIP Journal on Advances in Signal Processing, 2002, 2002(3): 316-329. DOI:10.1155/S1110865702000665 |
| [22] | GORE D A, HEATH R W, PAULRAJ A J. Transmit selection in spatial multiplexing systems[J]. IEEE Communications Letters, 2002, 6(11): 491-493. DOI:10.1109/LCOMM.2002.805517 |
| [23] | LU L, LI G Y, SWINDLEHURST A L, et al. An overview of massive MIMO:benefits and challenges[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 742-758. DOI:10.1109/JSTSP.2014.2317671 |
| [24] | BJOMSON E, LARSSON E G, MARZETTA T L. Massive MIMO:ten myths and one critical question[J]. IEEE Communications Magazine, 2015, 54(2): 114-123. |
| [25] | RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO:opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2012, 30(1): 40-60. |
| [26] | LI X W, WANG J, LI L, et al. Capacity bounds on the ergodic capacity of distributed MIMO systems over k fading channels[J]. Ksii Transactions on Internet & Information Systems, 2016, 10(7): 2992-3009. |
| [27] | LI X, LI J, LI L, et al. Effective rate of MISO systems over κ-μ shadowed fading channels[J]. IEEE Access, 2017, 5(13): 10605-10611. |




