2. 九江学院 理学院, 江西 九江 332005;
3. 软件工程国家重点实验室(武汉大学), 武汉 430072
2. College of Science, Jiujiang University, Jiujian Jiangxi 332005, China;
3. State Key Laboratory of Software Engineering(Wuhan University), Wuhan Hubei 430072, China
工业界和学术界各类数据规模的爆炸式增长,使得大规模数据处理技术成为各领域研究的热点,数据优化领域也进入了大规模时代。大规模黑盒优化问题高度复杂,无法采用传统的数学方法有效求解,其中决策变量的大规模性是构成求解难度的关键因素。进化计算是一类求解复杂优化问题的高效方法,过去二十多年的研究和应用表明,在小规模优化问题上进化算法取得了理想求解结果; 然而,当优化问题的规模迅速增大时,进化计算面临严重的挑战,求解性能恶化严重。如何利用进化计算方法,求解大规模优化问题,是目前科学和工程应用领域的研究热点。
1 相关工作当前,针对大规模优化问题的求解,学者们进行了多方面的研究工作,这些工作可归纳为以下两个方面。
一方面,基于先进的进化计算算法[1-3]进行改进,开发可靠性、精确性更高的进化计算算法(新的进化算子、混合进化模式、增强局部搜索、代理模型等),从而提高大规模优化问题的求解性能。如:文献[4]的研究证明将进化计算与其他技术进行混合,可以有效提高优化算法求解大规模问题的性能。文献[5]将高效的局部搜索技术与进化算法结合,提出一种文化基因算法(Memetic Algorithm, MA),该算法在一定程度上改善了复杂的组合优化问题的求解性能。文献[6]将正交交叉和反向学习结合,提出一种反向正交交叉的差分进化算法,实验结果表明,该算法对大规模优化问题的求解性能相对于其他几种知名的差分进化算法有明显的提升。文献[7]利用改进的精英学习进化算子和岛模型两种机制,对差分进化算法的优化性能进行改进,并将其部署到分布式平台Hadoop上,实验结果证明该方法可有效提高差分进化算法求解大规模优化问题的性能,同时具有较好的加速比。文献[8]提出一种代理模型辅助的群智能优化算法;该算法采用代理模型辅助的粒子群算法及基于粒子群的社会学习算法的协同优化来求解高维优化问题;两组不同维度的仿真实验结果表明,该方法所求得的解质量高于其他比较算法。
另一方面,引入协同进化思想,提高求解大规模优化问题的性能。协同进化思想的引入可分为两类。第一类,基于多个种群的协同进化。如文献[9]针对大规模数据优化问题,提出一种并行差分进化算法,该算法将协同进化思想引入到差分进化算法中,利用多个差分进化算法随机分解大规模优化问题,然后进行并行求解。该方法在大规模非线性函数优化问题的求解上取得了更高的精度和效率。文献[10]提出一种随机扩散搜索的协同差分进化算法,该算法利用随机扩散搜索策略将种群划分为成功和失败两个种群,利用不同进化策略并行协同进化,定期对两个种群进行信息交互。仿真实验表明该算法较基本差分进化和粒子群算法具有收敛速率和精度上的优势。第二类,基于分而治之的策略将大规模优化问题分解为多个子问题进行协同优化。如:文献[11]针对不可分问题提出一种决策变量随机分组(Random Grouping)的方法,该方法不考虑变量之间依赖关系,随机地划分变量分组。并通过多个轮次的进化,提高了相关变量进入同一分组的概率,一定程度上提高了大规模优化问题的求解效果。文献[12]针对固定大小的分组,深入分析了种群大小和分组大小对优化器求解性能的影响。在此基础上提出将部分评价资源用于对二者进行自适应调整的协同进化方法。实验表明该方法在分组大小固定的情况下,相对于其他CC框架具备一定的求解优势。文献[13]针对应用分而治之策略时子问题与原问题之间的维度匹配困难,提出一种自评价进化(Self-Evaluation Evolution, SEE)方法。SEE采用元模型技术来解决由于维度匹配困难所造成的高计算消耗问题,实验结果表明,SEE相对于四种代表性优化算法,在大规模优化问题的求解表现更为突出。文献[14]提出一种新的两阶段求解方法:第一阶段,检测搜索空间中变量之间的依赖关系,并据此形成变量的分组;第二阶段,依据经典的协同进化框架进行优化求解。文献[15]提出一种自动分组(Differential Grouping,DG)方法,能较为准确地发现决策变量之间的交互关系,并据此而形成相关变量的分组,一定程度上降低了各子分组之间的依赖关系,促进了大规模优化题求解性能的提升。
本文工作主要包括三方面:1)在DG算法的基础上,提出一种新的变量分组(New Different Grouping, NDG)方法, 进一步改善了基于加性可分原理进行变量分组的准确性;2)利用前期研究提出的CUDE(enhancing Differential Evolution with Commensal learning and Uniform local search)算法[16]设计子问题优化器,增强算法对子空间的寻优性能; 3)将以上改进引入协同进化框架,构建求解大规模优化问题的新型协同差分进化算法DECC-NDG-CUDE(Cooperative differential evolution with NDG and CUDE)算法,并在选定的测试集上进行仿真实验,实验结果表明,DECC-NDG-CUDE能进一步提高大规模优化问题的求解性能,是一种有效的算法。
2 新型变量分组策略 2.1 函数的加性可分性原理大规模黑盒优化问题由于其数学模型未知和不可获取,传统的数学方法,如求导法、单纯形法、梯度法等不再适用。针对这一情况,当前广泛采用的方法是通过对决策变量的分组,将问题分解成多个低维度的子问题来进行各个击破的独立求解。然而,当决策变量之间存在复杂的相互依赖关系时,盲目分组显然无法达到有效求解的目的。
基于加性可分性原理对变量之间的依赖关系进行先期学习,然后据此进行变量分组,可以最大限度地降低子问题之间的依赖关系,对提高求解性能有很大的促进作用。
定义1 如果函数f(x)满足如下条件:
| $ f\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^m {f\left( {{x_i}} \right)} $ | (1) |
则函数f(x)为加性可分解函数,其中x=(x1, x2, …, xm),xi为相互排斥的决策变量。
以二维函数f(x, y)为例,根据加性可分函数的定义可知:
若f(x, y)=f1(x)+f2(y),显然可得出f(x+Δx, y)-f(x, y)与y的无关。换句话说就是:f(x1, y)-f(x2, y)与y无关,即存在如下等式:
| $ f\left( {{x_1}, {y_1}} \right)-f\left( {{x_2}, {y_1}} \right) = f\left( {{x_1}, {y_2}} \right)-f\left( {{x_2}, {y_2}} \right) $ |
以此类推可得出如下推论:
n维函数f(x1, x2, …, xn),xi与xj之间加性可分,则存在如下等式:
| $ {f_{\left| {{x_i} = p, {x_j} = {t_1}} \right.}}-{f_{\left| {{x_i} = q, {x_j} = {t_1}} \right.}} = {f_{\left| {{x_i} = p, {x_j} = {t_2}} \right.}}-{f_{\left| {{x_i} = q, {x_j} = {t_2}} \right.}} $ | (2) |
其中i≠j, p≠q, t1≠t2;反之,若:
| $ {f_{\left| {{x_i} = p, {x_j} = {t_1}} \right.}}-{f_{\left| {{x_i} = q, {x_j} = {t_1}} \right.}} \ne {f_{\left| {{x_i} = p, {x_j} = {t_2}} \right.}}-{f_{\left| {{x_i} = q, {x_j} = {t_2}} \right.}} $ | (3) |
则xi与xj相互依赖,不可分。
式(2)和式(3)由加性可分性函数的定义导出,是函数加性可分的性质。
文献[15]利用式(2)构建了大规模优化问题自动分组(DG)算法。DG算法在可行域中选取4个测试点(边界和中心),计算式(2)左右两侧的两个差值Δ1和Δ2,通过比较表达式│Δ1-Δ2│的值和设定阈值的关系来判定决策变量之间是否存在依赖关系,进而形成变量分组。DG算法合理利用了函数加性可分的性质,能够较为准确地实现决策变量的分组。
然而,DG算法的实现仍然存在以下几个方面的不足:
1) 采用可行域的边界作为测试点;然而,边界本身具有特殊性,不能反映一般性。例如式(4)所示的函数:
| $ \begin{array}{l} f\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 2}^n {\left( {{x_i} * {x_{i-1}} * \left( {x_{i-1}^2-25} \right) * \left( {i - 1} \right)} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;{x_i} * {x_n} * \left( {x_i^2 - 25} \right) * n \end{array} $ | (4) |
设式(4)所示函数的定义域为[-5, 5]。假设n=4,则f(x)为4维函数。依据DG算法,用定义域的边界构造4个点,检测第一维和第二维的相关性,具体过程如下:
设p1=[-5, -5, -5, -5], p2=p1,p2(1)=5。由此,求Δ1为:
| $ {\Delta _1} = f\left( {{\mathit{\boldsymbol{p}}_1}} \right)-f\left( {{\mathit{\boldsymbol{p}}_2}} \right) $ | (5) |
设p3=p1, p4=p2, p3(2)=0, p4(2)=0, 由此,求Δ2为:
| $ {\Delta _2} = f\left( {{\mathit{\boldsymbol{p}}_3}} \right)-f\left( {{\mathit{\boldsymbol{p}}_4}} \right) $ | (6) |
| $ \left| {{\Delta _1}-{\Delta _2}} \right| $ | (7) |
则式(7)的值必定为0。据此,DG算法将第一维和第二维识别为不相关变量。此结论显然与函数本身的性质不符。
2) 排除已经形成分组的所有相关变量,导致依赖关系检测不全面,影响了分组的成功率。
3) 没有充分地利用分组学习阶段所获得的信息。比如将所有可分变量归为一个分组,当可分变量数量比较大时,所形成的分组规模较大,无法达到有效降维的目的,并且浪费了较多的评价资源。
2.2 新型分组算法为了进一步提高变量分组的精度,提高大规模优化问题的求解性能。针对DG算法3个不足进行改进,提出一种新的变量分组(NDG)算法。
首先,NDG算法避免采用可行域的边界作为测试点,而以边界附近的随机值为测试点。
其次,NDG算法采用遍历形式对变量相关性进行检测,也就说并不因为形成分组而排除某个变量的相关性检测,从而避免遗漏。
最后,为对相关性学习的结果进行充分利用,尤其是针对学习后判定为可分的变量组,若其大小仍然较大,则对其进行二次分组,进一步降低维度。
NDG算法的基本流程如下:
算法1 NDG(func, lbs, ubs, eps)
1) 设置Dims={1, 2, …, 1000}, 定义可分组变Seps,相关分组变量Cgroups,中间集合变量group, Agroups,Bgroups;初始化上下界变量lb,ub,评价次数变量FES=0;
2) while (Dims不为空)
3) group=[Dims(1)];
4) 定义两个1000维向量p1和p2, 各维在下界附近随机取值;
5) 将向量p2的第Dims(1)维设置为上届附近的随机值;
6) Δ1=f(p1)-f(p2),FES=FES+2
7) For i=2:length(Dims)
8) p3=p1;
9) p4=p2;
10) p3(i)=p4(i)=(lb+ub)/2
11) Δ2=f(p3)-f(p4),FES=FES+2;
12) if abs(Δ1-Δ2)>eps
group=[group, Dims(i)]
13) end if
14) end For循环
15) if length(group)==1
Seps=[Seps, group];
16) Else
Agroups={Agroups{1:end}, group}
group_u=union(group_u, group)
17) end if
18) if (length(Dims)>0)
设置Dims(1)=[]
19) end if
20) end while循环
21) 合并Agroup中包含相同元素的相关组,将结果赋值给Cgroup
22) 返回Seps,Cgroups;
其中,第4)和第5)步的随机值NDG采用上界或下界附近的随机值,有别于DG算法直接取上届或者下界。第12)步eps为阈值,当小于该阈值时,即认为两个差值相等。大于该阈值时,认为两个差值不相等。并以此判断变量之间的相关性。第22)步返回的可分组,在读取分组结果时进行判断,若仍然较大,则进行二次分组,按顺序每50个构成一个新的分组,最后一组为所有剩余变量。
3 基于改进差分进化算法的子问题优化器高效的优化器是提高大规模优化问题求解性能的有力工具。2016年文献[16]提出一种改进的差分进化算法(CUDE),实验表明CUDE寻优能力突出。为进一步提高求解大规模优化问题的性能,本文将CUDE作为子问题优化器引入到引入框架中。
3.1 改进的进化策略和参数调整方案缩放因子F和交叉概率CR是影响DE算法性能的两个核心参数。关于DE参数的大量研究已经证明固定的参数设置并非提高算法性能的最好设置。一般来说,较大的F和CR适合用于进化初期提升算法的全局搜索性能。而较小的F和CR适合在进化后期加强算法的局部开采性能,并加速收敛;然而,简单的前大后小的设置对提高算法的性能意义不大。
CUDE采用双边高斯分布进行F和CR的动态自适应更新。具体设置依据式(8)和(9)进行:
| $ {S_{{\rm{lower}}}} = \left\{ \begin{array}{l} {F_{{\rm{lower}}}} = N\left( {0.5, 0.1} \right)\\ C{R_{{\rm{lower}}}} = N\left( {0.1, 0.1} \right) \end{array} \right. $ | (8) |
| $ {S_{{\rm{upper}}}} = \left\{ \begin{array}{l} {F_{{\rm{upper}}}} = N\left( {0.8, 0.1} \right)\\ C{R_{{\rm{lower}}}} = N\left( {0.9, 0.1} \right) \end{array} \right. $ | (9) |
其中: N代表高斯函数,Slower和Supper代表双边参数设置的上、下界。
另外,为避免单一进化策略对问题的依赖性,CUDE选择DE/rand/1、DE/best/1、DE/target-to-rand/1三种进化策略与双边高斯参数设置进行组合使用。
对双边高斯参数设置和三种进化策略,进行两两组合,共构造6种进化方案。然后,在每一代进化中CUDE采用轮盘赌的方式为每一个个体从6种方案中选择一个进行进化。在每一代进化之后,记录每个方案对种群中每个个体的成功更新次数Ssch, i和尝试更新次数Tsch, i,并进行相除得到更新成功率参数SRsch, i,SRsch, i的计算公式如式(10)所示:
| $ S{R_{sch, i}} = {S_{sch, i}}/{T_{sch, i}} $ | (10) |
依据SRsch, i,构建学习字典二维表。在下一代中依据学习字典,采用轮盘赌的方式选择每个个体的进化方案。
3.2 基于均匀设计的局部搜索采用基于均匀设计(Uniform Local Search,ULS)的局部搜索技术,CUDE有效地平衡了DE算法的勘探和开采能力。均匀设计是一种高质量的实验设计方法,其基础理论为数论中的一致分布理论,最早由Wang等[17]和Fang等[18]提出。与同为实验设计方法的正交设计相比,均匀设计的优势是实验次数更少,这在以个体适应度为评价体的进化算法中尤为重要。近年来已有不少学者将均匀设计引入到进化计算算法中,如文献[19]在利用均匀设计来进行算法种群的初始化。
均匀设计依据均匀设计表来安排实验方案。一个均匀设计表可表示为Un(qS), 其中n为表的行数,代表要安排的实验次数;S为列数,代表要考虑的因素数;q代表每个因素要考虑的水平数。CUDE所采用的ULS局部搜索方法,选择均匀设计表U6(66)进行实验方案安排。关于U6(66)的构造参考文献[16]。
| 表 1 均匀设计表U6(66) Table 1 Uniform design table U6(66) |
CUDE采用以上两个方面的改进提高了算法的寻优能力,算法详细流程及参数见文献[16]。
ULS在每一代进化中随机选择两个个体进行局部搜索。以二维空间为例,假设所选取的两个个体为A(x1, y2)和B(x2, y2)。则ULS首先会将A和B构成的二维子空间的每一维均匀地分解成6个部分,每个部分看作一个因素。然后,依据均匀设计表U6(66)组合每个水平上的各个因素,构造出6个实验体。最后,对6个实验个体进行评价,选择最优的替换A和B的一个完成局部搜索。ULS的详细流程如算法2。需说明的是ULS在进化的每一代中仅执行一次。
算法2 ULS算法。
1) 输入:种群P,评价次数计数器FEs。
2) 从P中随机选择两个个体xi, g和xj, g。
3) 根据xi, g和xj, g,利用U6(66)进行均匀,产生6个实验个体y1, y2, …, y6。
4) 评价6个实验个体。
5) 选取适应度最高的一个实验个体O。
6) 用O替换当前种群P中的个体xi, g,替换条件为f(xi, g)>f(o)。
7) FEs=FEs+6。
8) 返回新种群P和参数FEs。
3.3 协同进化框架为了进一步提高求解大规模优化问题的性能,将NDG和CUDE引入到协同进化框架之下,构建DECC-NDG-CUDE算法(算法3)。
算法3 DECC-NDG-CUDE(func, lbs, ubs, n)。
1) groups=NDG(func, lbs, ubs)
2) pop=rand(popsize, n)
3) (best, best_val)=min(func(pop))
4) for i=1 to cycles do
5) for j=1 to size(groups) do
6) indicies=groups[j];
7) subpop=pop[:, indicies]
8) subpop=CUDE(best, subpop, FEs)
9) pop[:, indicies]=subpop
10) (best, best_val)=min(func(pop))
11) end for
12) end for
4 实验与分析为了合理公平地评价NDG算法对变量进行分组的准确性和有效性,本文仿真分别进行分组和优化两个实验。分组实验验证NDG对变量分组的准确性,并将分组结果和文献[15]的DG方法进行比较,优化实验验证了DECC-NDG-CUDE求解大规模优化问题的性能,并将实验结果与DECC-DG(Differential Evolution with Cooperative Co-evolution and differential Grouping)[15]、DECCG(Differential Evolution with Cooperative Co-evolution and Random Grouping)[11]两种算法进行比较。
4.1 测试问题为保证真实性、有效性,选取CEC2010[20]标准测试集的10个1000维的问题进行仿真实验。10个问题的特征信息如表 2所示。
| 表 2 变量分组结果(ε=10-1) Table 2 Grouping result(ε=10-1) |
| $ {f_1}\left( x \right) = \sum\limits_{i = 1}^D {\left[{z_i^2-10\cos \left( {2{\rm{ \mathsf{ π} }}{z_i}} \right) + 10} \right]} $ |
其中:可分变量数(Sep_Vars)为1000,不可分变量数(NonSep_Vars)为0,不可分变量组数(NonSep_Groups)为0。
| $ \begin{array}{l} {f_2}\left( x \right) =-20\exp \left( {-0.2\sqrt {\frac{1}{D}\sum\limits_{i = 1}^D {z_i^2} } } \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\exp \left( {\frac{1}{D}\sum\limits_{i = 1}^D {\cos \left( {2{\rm{ \mathsf{ π} }}{z_i}} \right)} } \right) + 20 + {\rm{e}} \end{array} $ |
其中:Sep_Vars为1000,NonSep_Vars为0,NonSep_Groups为0。
| $ \begin{array}{l} {f_3}\left( x \right) = {f_{{\rm{rot\_rastrigin}}}}\left[{z\left( {{P_1}:{P_m}} \right)} \right] * {10^6} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{rastrigin}}}}\left[{z\left( {{P_{m + 1}}:{P_D}} \right)} \right] \end{array} $ |
其中:Sep_Vars为950,NonSep_Vars为50,NonSep_Groups为1。
| $ \begin{array}{l} {f_4}\left( x \right) = \sum\limits_{k = 1}^{D/2m} {{f_{{\rm{rot\_rastrigin}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{rastrigin}}}}\left[{z\left( {{P_{D/2 + 1}}:{P_D}} \right)} \right] \end{array} $ |
其中:Sep_Vars为500,NonSep_Vars为500,NonSep_Groups为10。
| $ \begin{array}{l} {f_5}\left( x \right) = \sum\limits_{k = 1}^{D/2m} {{f_{{\rm{rot\_ackley}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{ackley}}}}\left[{z\left( {{P_{D/2 + 1}}:{P_D}} \right)} \right] \end{array} $ |
其中:Sep_Vars为500,NonSep_Vars为500,NonSep_Groups为10。
| $ \begin{array}{l} {f_6}\left( x \right) = \sum\limits_{k = 1}^{D/2m} {{f_{{\rm{schwefel}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{sphere}}}}\left[{z\left( {{P_{D/2 + 1}}:{P_D}} \right)} \right] \end{array} $ |
其中:Sep_Vars为500,NonSep_Vars为500,NonSep_Groups为10。
| $ {f_7}\left( x \right) = \sum\limits_{k = 1}^{D/m} {{f_{{\rm{rot\_rastrigin}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} $ |
其中:Sep_Vars为0,NonSep_Vars为1000,NonSep_Groups为20。
| $ {f_8}\left( x \right) = \sum\limits_{k = 1}^{D/m} {{f_{{\rm{rot\_ackley}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} $ |
其中:Sep_Vars为0,NonSep_Vars为1000,NonSep_Groups为20。
| $ {f_9}\left( x \right) = \sum\limits_{k = 1}^{D/m} {{f_{{\rm{rosenbrock}}}}\left[{z\left( {{P_{\left( {k-1} \right) * m\left| { + 1} \right.}}:{P_{k * m}}} \right)} \right]} $ |
其中:Sep_Vars为0,NonSep_Vars为1000,NonSep_Groups为20。
| $ {f_{10}}\left( x \right) = \sum\limits_{i = 1}^{D- 1} {\left[{100{{\left( {z_i^2-{z_{i + 1}}} \right)}^2} + {{\left( {{z_i}-1} \right)}^2}} \right]} $ |
其中:Sep_Vars为0,NonSep_Vars为1000,NonSep_Groups为1。
f1(x)~f10(x)表达式中,x=(x1, x2, …, xD)为候选解;z=x-o为偏移候选解,o=(o1, o2, …, oD)全局最优解;P是{1, 2, …, D}的一个随机排列,D为问题维度。
4.2 分组实验结果与分析分组实验中利用NDG算法对10问题进行变量分组,检验NDG算法对变量之间相关性的识别并依据其形成变量组的性能。为比较充分地验证NDG的性能,实验分别在两种阈值(10-1和10-3)情况下进行实验,记录算法识别的可分变量数、相关变量数、相关变量分组数以及相关变量的识别成功率(所识别的相关变量除以相关变量总数),并将结果和文献[15]中知名的算法DG进行对比。实验结果见表 2和表 3。
| 表 3 变量分组结果(ε=10-3) Table 3 Grouping result(ε=10-3) |
表 2和表 3的分组结果显示,在两种阈值下,对两个完全可分的问题f1、f2上,NDG和DG算法都能准确的识别出为完全可分问题,说明两种算法能准确的区分出可分解的决策变量;在两种阈值下,对f3、f4、f6三个部分可分解问题上,NDG和DG算法的结果相同,能准确的识别出可分解变量和相关变量,说明两种算法对着三个问题的分解没有受到阈值的影响,成功识别了变量的相关性,并且相关变量的分组也准确无误。
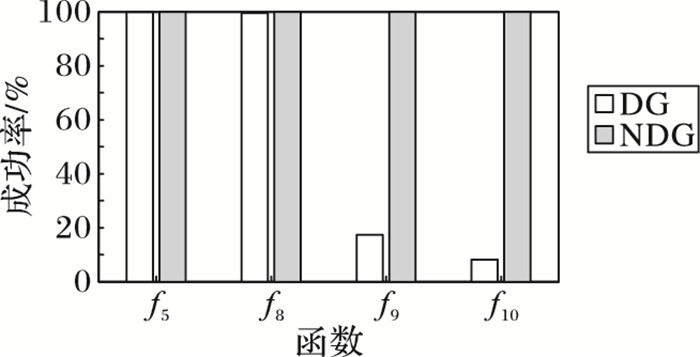
在f5、f7、f8、f9、f10部分可分的问题上,NDG和DG两种算法表现出不同的性能。在阈值为10-1时,对问题f10两种算法分组结果相同;在阈值为10-3时,DG算法对相关变量的识别成功率较低,仅有8.2%。而NDG算法仍能准确地识别出所有变量为相关变量,且相关变量分组也准确无误。这一结果表明,对问题f10,DG算法受到了阈值设置的影响,在较小阈值的设置下,不能准确识别相关量,性能弱于NDG算法;对问题f7,在阈值10-3时,两种算法表现相同,均能有效识别变量的相关性,并准确分组;在阈值为10-1时,算法DG未能完全识别相关变量,但只有1个相关变量未能准确识别,成功率为99%。而NDG算法能准确识别所有变量的相关性,性能略优于DG算法。
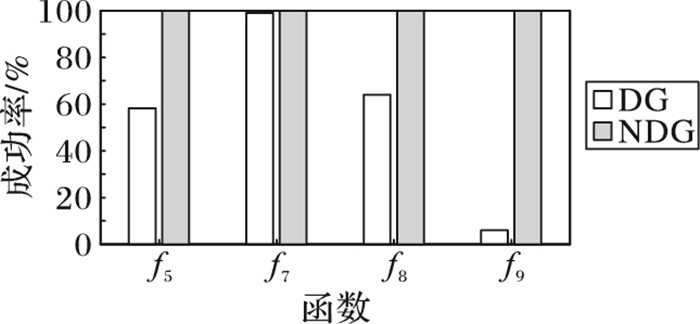
在其他的三个问题f5、f8、f9上,DG算法均对变量的相关性识别的成功率均未达到100%,即没有准确识别所有相关变量,其中f9在两种阈值下的相关变量识别均非常低。f5、f8两个问题的相关变量的识别率,在阈值为10-1时分别为58.2%和64%,在阈值为10-3时分别为99.8%和99.6%。说明DG算法对这两个问题的分解受到阈值的影响较大。然而,NDG算法在两种阈值下,对于三个问题均能准确识别变量的相关性,且分组未出现差错。
综上所述,对于选定的10个大规模问题,NDG算法对变量相关性的识别性能整体上优于DG算法,能准确识别出相关变量并形成相关组。
图 1和图 2给出了存在差别的几个问题上相关变量识别成功率的柱状图,进一步比较了两种算法分组性能的区别。
|
图 1 捕获不可分变量成功率(ε=10-1) Figure 1 Success rate of capturing nonseparables variables(ε=10-1) |
|
图 2 捕获不可分变量成功率(ε=10-3) Figure 2 Success rate of capturing nonseparables variables(ε=10-3) |
优化实验验证DECC-NDG-CUDE算法对10个问题的优化求解性能。实验中各参数的设置为优化问题维度D=1000,种群popsize=50,进化结束条件为适应度评价次数FEs=3E6。实验独立执行25次,记录最优解的平均值和方差。同时,为进行对比分析,实现了DECCG[7]、DECC-DG[9]算法,依据原文先相同设置进行仿真实验,并记录结果。实验结果见表 4。
| 表 4 优化实验结果 Table 4 Optimization results |
从表 4的求解结果均值来看,与DECC-DG算法相比,DECC-NDG-CUDE在7个问题上优于算法DECC-DG,3个问题上差于算法DECC-DG;与DECCG算法相比,DECC-NDG-CUDE在7个问题上优于算法DECCG,3个问题上差于DECCG。这说明DECC-NDG-CUDE算法求解10个大规模问题的数据结果整体上优于DECC-DG和DECCG两种算法结果。
为了保证以上数据结果的真实性,采用显著水平为0.05的秩和检验(Wilcoson test)对两种算法的实验数据进行检验,检验结果用三种符号“+”“-”“≈”标注在表 4中。
表 4中,“+”“-”“≈”分别表示DECC-NDG-CUDE算法弱于、优于和相当于对比算法(DECC-DG或DECCG)。首先,从检验统计结果来看,DECC-NDG-CUDE在6个问题(f1、f4、f6、f7、f9、f10)上是优于DECC-DG、3个问题(f2、f5、f8)上弱于DECC-DG、1个问题(f5)上与DECC-DG算法相当。这表明在f5上,与DECC-DG相比,DECC-NDG-CUDE数据结果的优势存在偶然性,实际两个算法的结果不存在差别。其次,与DECCG的检验结果与数据结果一致,这说明DECC-NDG-CUDE在这7个问题上的求解性能优于DECCG是真实的,与数据比较结果一致。
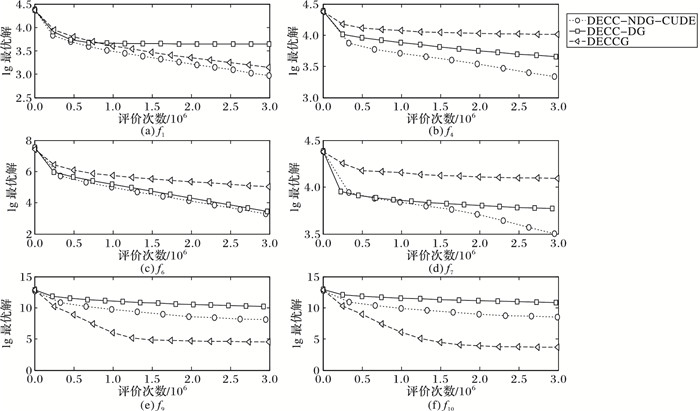
图 3给出了其中6个问题的收敛曲线。需要说明的是,在f9和f10两个问题的收敛图中,DECC-NDG-CUDE的收敛曲线差于DECCG,其原因是这两个函数为完全不可分问题,DECC-NDG-CUDE变量相关性识别损失了较多的评价资源,影响了后期的优化效果。但是,从6幅图的整体情况来看,收敛曲线仍然支持了以上数据分析的结果。
|
图 3 三种算法在6个问题上的收敛曲线 Figure 3 Convergence curve of three algorithms on six problems |
最后,为整体上比较三种算法求解10个大规模优化问题的性能,对三种算法优化结果进行Friedman排名检验,检验结果为,DECC-NDG-CUDE的排名值为1.60,DECC-DG排名值为2.10,DECCG排名值为2.30。因此,DECC-NDG-CUDE的Friedman检验排名第一,整体性能最好。
综上所述,DECC-NDG-CUDE算法对于10个优化问题的优化性能在整体上优于DECC-DG和DECCG两种算法。
5 结语针对大规模优化问题,本文首先提出一种改进的分组方法NDG,该算法采用随机选取测试点,逐一检测每对决策变量的相关性,并依据相关性对变量进行分组,从而将大规模优化问题划分为多个子问题,降低了子问题之间的依赖关系; 同时,为了充分利用变量相关性的学习结果,将较大的可分变量组进行二次分组,在不影响相关组的情况下,降低了待优化子问题的维度。仿真实验表明NDG算法提高了变量分组的精确度,能够对协同优化求解起到促进作用;另一方面,为进一步提高优化问题求解进度,在改进的差分进化算法CUDE的基础之上,设计新的子问题优化器,并引入到CC框架之下,构建DECC-NDG-CUDE算法。优化仿真实验的结果表明,在10个大规模优化问题上,DECC-NDG-CUDE能够进一步提高求解精度,求解性能优于DECC-DG和DECCG两种知名算法,是求解大规模优化问题的一种有效的算法。在未来的研究工作中,将深入探索优化过程中降低函数评价次数的合理途径,从而减少因变量分组消耗评价次数对问题优化带来的影响。
| [1] | STORN R, PRICE K. Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [2] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ:IEEE, 1995:1942-1948. http://www.oalib.com/references/8710652 |
| [3] | KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization:Artificial Bee Colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [4] | GOLDBERG D E, VOESSNER S. Optimizing global-local search hybrids[EB/OL].[2016-11-20].http://pdfs.semanticscholar.org/21b8/ae2a75de794a625df6737466483d93441f9b.pdf. |
| [5] | FACHBEREICH V, INFORMATIK E. Memetic algorithms for combinatorial optimization problems:fitness landscapes and effective search strategies[EB/OL].[2016-11-20].http://dokumentix.ub.uni-siegen.de/opus/volltexte/2006/181/pdf/merz.pdf. |
| [6] | DENG C, DONG X, YANG Y, et al. Differential evolution with novel local search operation for large scale optimization problems[C]//Proceedings of the 6th International Conference Advances in Swarm and Computational Intelligence. Berlin:Springer, 2015, 9140:317-325. |
| [7] | 董小刚, 邓长寿, 袁斯昊, 等. MapReduce模型下的分布式差分进化算法[J]. 小型微型计算机系统, 2016, 37(12): 2695-2701. (DONG X G, DENG C S, YUAN S H, et al. Distributed differential evolution algorithm based on MapReduce model[J]. Journal of Chinese Computer Systems, 2016, 37(12): 2695-2701. DOI:10.3969/j.issn.1000-1220.2016.12.020) |
| [8] | SUN C, JIN Y, CHENG R, et al. Surrogate-assisted cooperative swarm optimization of high-dimensional expensive problems[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(4): 644-660. DOI:10.1109/TEVC.2017.2675628 |
| [9] | 刘剑英. 基于GPU的并行协同差分进化算法研究[J]. 计算机工程与应用, 2012, 48(7): 48-50. (LIU J Y. Research of parallel cooperation differential evolution algorithm based on GPU[J]. Computer Engineering and Applications, 2012, 48(7): 48-50.) |
| [10] | 张大斌, 周志刚, 叶佳, 等. 基于随机扩散搜索的协同差分进化算法[J]. 计算机工程, 2014, 40(7): 183-188. (ZHANG D B, ZHOU Z G, YE J, et al. Cooperation differential evolution algorithm based on stochastic diffusion search[J]. Computer Engineering, 2014, 40(7): 183-188.) |
| [11] | YANG Z, TANG K, YAO X. Large scale evolutionary optimization using cooperative coevolution[J]. Information Sciences, 2008, 178(15): 2985-2999. DOI:10.1016/j.ins.2008.02.017 |
| [12] | TRUNFIO G A, TOPA P, WAS J. A new algorithm for adapting the configuration of subcomponents in large-scale optimization with cooperative coevolution[J]. Information Sciences, 2016, 372: 773-795. DOI:10.1016/j.ins.2016.08.080 |
| [13] | YANG P, TANG K, YAO X. Turning high-dimensional optimization into computationally expensive optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(9): 1-14. |
| [14] | CHEN W, WEISE T, YANG Z, et al. Large-scale global optimization using cooperative coevolution with variable interaction learning[C]//Proceedings of the 11th International Conference on Parallel Problem Solving from Nature. Berlin:Springer-Verlag, 2010:300-309. https://link.springer.com/chapter/10.1007/978-3-642-23424-8_1 |
| [15] | OMIDVAR M N, LI X, MEI Y, et al. Cooperative co-evolution with differential grouping for large scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 378-393. DOI:10.1109/TEVC.2013.2281543 |
| [16] | PENG H, WU Z, DENG C. Enhancing differential evolution with commensal learning and uniform local search[J]. Chinese Journal of Electronics, 2017, 26(4): 725-733. DOI:10.1049/cje.2016.11.010 |
| [17] | WANG Y, FANG K. A note on uniform distribution and experiment design[J]. Science Bulletin, 1981, 26(6): 485-489. |
| [18] | FANG K, MA C, WINKER P, et al. Uniform design:theory and application[J]. Technometrics, 2000, 42(3): 237-248. DOI:10.1080/00401706.2000.10486045 |
| [19] | PENG L, WANG Y. Differential evolution using uniform-quasi-opposition for initializing the population[J]. Information Technology Journal, 2010, 9(8): 1629-1634. DOI:10.3923/itj.2010.1629.1634 |
| [20] | TANG K, LI X, SUGANTHAN P N, et al. Benchmark functions for the CEC'2010 special session and competition on large-scale global optimization[EB/OL].[2016-11-20].http://goanna.cs.rmit.edu.au/~xiaodong/publications/lsgo-cec10.pdfhttp://goanna.cs.rmit.edu.au/~xiaodong/publications/lsgo-cec10.pdf. |




