在过去20年里,支持向量机(Support Vector Machine, SVM)已经吸引了广泛的关注[1-4]。SVM的核心思想是通过最大化两个边界平面(Bounding planes)间的间隔来搜寻最优分类平面。这两个平面各自归属于一个特定的类,且具有平行的特性。
近些年,近似多平面SVM技术得到了学者们广泛研究。不同于基于两平行平面的SVM方法,近似多平面SVM旨在为每类找一个最好的拟合平面,平面间不需要保证平行的条件。Mangasarian等[5]提出的广义特征值近似SVM(Proximal Support Vector Machine via Generalized Eigenvalues, GEPSVM),通过构建带有每个平面离本类样本近而离它类样本远几何解释的目标问题,来找两个拟合平面,最终,问题归结为解两个广义特征值问题。GEPSVM的这些独特性保证了它的计算优势以及好的分类性能,尤其在异或(Exclusive OR, XOR)问题上, 其往往是SVM无法超越的。
随后,许多研究人员对GEPSVM进行了拓展。Guarracino等[6]提出了正则化的特征值分类器(Regularized Generalized Eigenvlue Classifier, ReGEC)。与GEPSVM相比,ReGEC的一个主要优势在于, 在二分类问题上计算时间要减少一半,因其仅要求解一个而非两个广义特征值问题。Jayadeva[7]模糊化GEPSVM,建立了模糊GEPSVM(Fuzzy GEPSVM, FGEPSVM)模型。杨绪兵等[8-9]提出了基于原型超平面的多类最接近支持向量机(Mult-class Hyperplane Proximal SVM, MHPSVM)和局部化的广义特征值最接近支持向量机(Localized Proximal Support Vector Machine via Generalized Eigenvalues, LGEPSVM), Ye等和Shao等[11]提出了多权向量投影支持向量机(Multi-Weight Vector Projection Support Vector Machine, MVSVM)。Shao等[11]改进GEPSVM成一个差形式。这些方法大多都采用商形式。基于GEPSVM另一种拓展是对支持向量机(TWin SVM, TWSVM)[12-19],其共同之处在于都解二次凸规划而非广义特征值问题。与GEPSVM相比, TWSVM除计算上存在较大劣势外,在求解XOR问题上也不足够理想[15]。
GEPSVM或者它的相关拓展中大多数方法对野值或噪声存在敏感性,因其在模型中采用了L2范数平方距离[17-18]。近年,文献[17-20]揭露L1范数距离对野值具较好的鲁棒性。Kwak等[20]首次将L1范数距离引入主成分分析(Principal Component Analysis, PCA)中,随后L1范数距离被应用于线性判别分析(Linear Discriminant Analysis, LDA)特征抽取的判别准则中[18-19]。启发于基于L1范数距离相关的特征抽取方法,Li等[17]提出了鲁棒L1范数非平行近似支持向量机(L1-norm Nonparallel SVM, L1-NPSVM), 其将GEPSVM中L2范数平方距离用L1范数距离来代替,从而保证了GEPSVM对野值或噪声的鲁棒性。L1-NPSVM形式上与GEPSVM相同,即:一个商形式,但因其非凸性且目标包含绝对值计算,使模型不易求解。为了获得解,文献[17]采用梯度上升(Gradient Ascending, GA)迭代算法。GA本质上是与梯度下降(Gradient Descending, GD)算法相同,差异仅仅在于目标为最大还是最小化问题。这样需要引入一个学习率,正如文献[19]所指,其还需要引入一个非凸的代替函数,因其非凸性,学习率不适当的选择影响着解的最优性。文献[21]中,Kwak也进一步指出了GD导致不令人满意的结果。导致这样问题还可能因为,与GA相同,GD学习率的选择不应过大,否则它不收敛,且其大小也影响着其收敛速度,在保证收敛的情况下,学习率越大收敛得越快,而越小收敛得越慢[17];L1-NPSVM算法中仅仅包含了一个参数——学习率,事实上,其在模型中起着调整模型泛化能力的作用,然而,为了保证收敛性,其学习率的选择受到众多限制,以至于往往无法保证获得最优性能。针对GEPSVM对野值或噪声不鲁棒的问题,本文同样也展开了研究,基于L1-NPSVM目标问题,提出一个更有效的迭代算法。该算法能保证快速地收敛,且因每次迭代解线性方程而继承了GEPSVM的计算上的优势,从理论上证明了所提算法的收敛性。最后实验揭露所提算法的可靠性。
1 相关工作在一个n维空间考虑二分类问题。假定有m个训练两类样本{(xj(i), yi)|i=1, 2, j=1, 2, …, mi},xj(i)指第i类第j个样本,且m1+m2=m,yj∈{-1, 1}是样本的类标记,其表示正负两类。进一步用m1×n的矩阵A和m2×n的矩阵B描述。定义两个元素全为1的列向量e1∈Rm1和e2∈Rm2,让(w1, b1)和(w2, b2)分别为正负类平面的权向量和偏差。所有公式中的T均表示向量(矩阵)转置。
1.1 广义特征值近似支持向量机首先回顾下经典的多平面分类器GEPSVM[5],其旨在缓解传统支持向量机代价高且无法较理想地求解如XOR等较复杂的问题。为了获得如下两个最优的非平行的平面:
| $ {\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{w}}_{^1}} + {\mathit{\boldsymbol{e}}_{^1}}{b_{^1}} = 0 $ | (1) |
| $ {\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{w}}_2} + {\mathit{\boldsymbol{e}}_{^2}}{b_{^2}} = 0 $ | (2) |
GEPSVM建立两个新颖的目标问题,其要求平面离本类样本尽可能地近, 而离它类样本尽可能地远。这两个问题的具体形式分别定义为:
| $ \min \frac{{||\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{w}}_1} + {\mathit{\boldsymbol{e}}_1}{b_1}|{|^2} + {\rm{ \mathsf{ δ} }}||[{\mathit{\boldsymbol{w}}_1}^{\rm{T}},{b_1}]|{|^2}}}{{||\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_1} + {\mathit{\boldsymbol{e}}_2}{b_1}|{|^2}}} $ | (3) |
| $ \min \frac{{||\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_2} + {\mathit{\boldsymbol{e}}_2}{b_2}|{|^2} + {\rm{ \mathsf{ δ} }}||[{\mathit{\boldsymbol{w}}_2}^{\rm{T}},{b_2}]|{|^2}}}{{||\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{w}}_2} + {\mathit{\boldsymbol{e}}_1}{b_2}|{|^2}}} $ | (4) |
其中δ是正则化参数。注意正则化项是为了改进GEPSVM的泛化能力。
令H=[A e1],G=[B e2],z1=[w1T b1]T,z2=[w2T b2]T。简化上述问题(3)和(4),得到式(5)和(6):
| $ \min \frac{{{\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{z}}_1} + δ{\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{z}}_1}}}{{{\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{z}}_1}}} $ | (5) |
| $ \min \frac{{{\mathit{\boldsymbol{z}}_2}^{\rm{T}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{z}}_2} + δ{\mathit{\boldsymbol{z}}_2}^{\rm{T}}{\mathit{\boldsymbol{z}}_2}}}{{{\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{z}}_1}}} $ | (6) |
上述问题(5)和(6)是两个典型的Rayleigh商问题,因此,它们的解归结为求解两个广义特征值问题,即:(HTH+δI)z1=λ1GTGz1和(GTG+δI)z1=λ1HTHz1,其解为该特征方程最小特征值对应的特征向量。给定一个测试样本x,将其归属于其距最近的平面所属的类。
1.2 鲁棒L1范数非平行近似支持向量机从GEPSVM的两个模型(3)和(4)中可以看出,GEPSVM度量点到平面的距离用L2范数的平方。自然地,为了获得目标函数的最小值,GEPSVM不得不强调那些偏远于同类的样本的作用,说明L2范数易夸大野值或噪声的影响。平方L2范数距离度量易受野值或噪声的影响,而L1范数距离度量具有较强的鲁棒性[18-19]。鉴于L1范数距离的鲁棒性,Li等[17]提出了L1-NPSVM, 其直接将GEPSVM原目标问题中L2范数平方距离替换为L1范数距离,其具体形式描述为:
| $ \min \frac{{||\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{w}}_1} + {\mathit{\boldsymbol{e}}_1}{b_1}|{|_1}}}{{||\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_1} + {\mathit{\boldsymbol{e}}_2}{b_1}|{|_1}}} $ | (7) |
| $ \min \frac{{||\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_2} + {\mathit{\boldsymbol{e}}_2}{b_2}|{|_1}}}{{||\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{w}}_2} + {\mathit{\boldsymbol{e}}_1}{b_2}|{|_1}}} $ | (8) |
令gi∈R1×(n+1)和hi∈R1×(n+1)为矩阵G和H的第i行。简化式(7)和(8)为:
| $ \min \sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1}|} /\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1}|} $ | (9) |
| $ \min \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_2}|} /\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2}|} $ | (10) |
上面问题包括了绝对值操作,是两个非凸问题。为了对其进行求解,Li等[17]用如下迭代程序对其进行求解。以问题(9)开始,本文阐述这个迭代程序。定义z1(p)为第p次迭代获得的解,那么,z1(p+1),即在p+1次迭代的解能通过下列等式获得:
| $ \mathit{\boldsymbol{z}}_1^{(p + 1)} = \mathit{\boldsymbol{z}}_1^{(p)} + \beta g(\mathit{\boldsymbol{z}}_1^{(p)}) $ | (11) |
其中β是学习率,一个较小的正实数,而:
| $ \mathit{\boldsymbol{g}}(\mathit{\boldsymbol{z}}_1^{(p)}) = \frac{{\sum\limits_{i = 1}^{{m_1}} {{\rm{sign}}({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)}){\mathit{\boldsymbol{h}}_i}^{\rm{T}}} }}{{\sum\limits_{i = 1}^{{m_1}} {{\rm{|}}{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} }} - \frac{{\sum\limits_{i = 1}^{{m_2}} {{\rm{sign}}({\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}){\mathit{\boldsymbol{g}}_i}^{\rm{T}}} }}{{\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} }} $ | (12) |
是对应的梯度方向,sign(·)为符号函数,其定义为:如果(·)是一个负数,其值为-1, 否则为1。通过z1(p+1)=z1(p+1)/‖z1(p+1)‖2对z1(p+1)进行归一化。继续迭代直到找到最优解。
2 建议的方法实际上,L1-NPSVM将问题(9)和(10)重写为如下两个等价的最大化问题:
| $ {\rm{max}}\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_2}|} /\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2}|} $ | (13) |
| $ {\rm{max}}\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2}|} /\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_2}|} $ | (14) |
因为问题(12)的梯度方向g(z1(p))是目标问题(13)在点z1(p)的梯度,所以,上述迭代程序是梯度上升GA算法[18-19]。
基于L1范数距离的相关工作起源于Kwak[20]提出的L1范数PCA(L1-PCA)。近年,其思想也延伸到线性判别分析LDA中,由此出现了基于L1范数距离LDA(L1-LDA)[18-19]。较L1-PCA,L1-LDA面对更大的挑战是如何解同时最大最小的L1范数距离的目标问题。形式上,GEPSVM相似于LDA, 差异仅仅在于前者为实现分类问题计算同类和不同类点与平面间的距离,而后者为实现特征提取问题计算类间和类内距离。同样,L1-NPSVM形式上也与L1-LDA相同,目标是个同时最大最小问题。当将式(3)和式(7)以及式(13)和式(14)进行比较可知,除L1范数距离度量,L1-NPSVM与GEPSVM问题最大不同之处还在于它不考虑正则项,旨在减少不定参数数目,因其包括了学习率的选择。正则项的引入GEPSVM, 起初目的是改进模型的泛化能力[5],那么,学习率的选择对L1-NPSVM的泛化能力起着决定性的作用。
为了解L1-LDA, 文献[18]GD对其进行求解。然而,后续工作[19]却指出,因GD需要引入一个非凸的代替函数且其非凸性导致学习率的不适当选择引起L1-LDA无法获取有效的解。在文献[21]中,Kwak也进一步指出了这样迭代算法易导致不令人满意的结果。正如上节所指出,L1-NPSVM也用不完美的GD对其目标进行求解。GD的不足,也可能由如下原因所致,本文直接基于L1-NPSVM问题对其分析。GD本质上与GA相同, 其学习率的选择不应过大,否则它不收敛,且其大小也影响着其收敛速度,在保证收敛的情况下,学习率越大收敛得越快,而越小收敛得越慢[17]。这意味着,学习率的选择受到众多限制,而它在L1-NPSVM充当控泛化能力的作用,以至于往往无法保证获得的性能是最优的。
为了缓解GD的不足,文献[19]首先将一个最小化商问题转换为一个等价的带约束问题,进一步提出一个有效迭代算法对其进行求解。这里,本文拓展该算法到解L1-NPSVM问题。本文以直接解L1-NPSVM中最大化商而非最小化商问题(13)和(14)为目的。首先,这两个问题转换为如下两个等价的带等式约束的最大化问题:
| $ \begin{array}{r} {\rm{max}}\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1}|} \\ \;{\rm{s}}{\rm{.t}}{\rm{.}}\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1}|} = 1 \end{array} $ | (15) |
| $ \begin{array}{r} {\rm{max}}\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2}|} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_2}|} = 1 \end{array} $ | (16) |
注意,z1和z2规模的变化不会导致原问题目标值的变化[19]。因为
| $ \sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1}|} = {\mathit{\boldsymbol{z}}_1}^{\rm{T}}\left( {\sum\limits_{i = 1}^{{m_1}} {\frac{{{\mathit{\boldsymbol{g}}_i}^{\rm{T}}{\mathit{\boldsymbol{g}}_i}}}{{|{\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1}|}}} } \right){\mathit{\boldsymbol{z}}_1}{\rm{ = }}\sum\limits_{i = 1}^{{m_1}} {{\rm{sign}}({\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1})({\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_1})} $ | (17) |
| $ \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1}|} = {\mathit{\boldsymbol{z}}_1}^{\rm{T}}\left( {\sum\limits_{i = 1}^{{m_2}} {\frac{{{\mathit{\boldsymbol{h}}_i}^{\rm{T}}{\mathit{\boldsymbol{h}}_i}}}{{|{\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1}|}}} } \right){\mathit{\boldsymbol{z}}_1}{\rm{ = }}\sum\limits_{i = 1}^{{m_2}} {{\rm{sign}}({\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1})({\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1})} $ | (18) |
令dii=1/|giz1|,fii=1/|hiz2|,si=sign(hiz1),ki=sign(giz1),可以重写问题(15)和(16)为:
| $ \begin{array}{c} {\rm{min}}\sum\limits_{i = 1}^{{m_2}} {{s_i}({\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1})} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\mathit{\boldsymbol{z}}_1}^{\rm{T}}(\sum\limits_{i = 1}^{{m_1}} {{d_{ii}}{\mathit{\boldsymbol{g}}_i}^{\rm{T}}{\mathit{\boldsymbol{g}}_i}} ){\mathit{\boldsymbol{z}}_1} = 1 \end{array} $ | (19) |
| $ \begin{array}{c} {\rm{min}}\sum\limits_{i = 1}^{{m_1}} {{k_i}({\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2})} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\mathit{\boldsymbol{z}}_2}^{\rm{T}}(\sum\limits_{i = 1}^{{m_2}} {{f_{ii}}{\mathit{\boldsymbol{h}}_i}^{\rm{T}}{\mathit{\boldsymbol{h}}_i}} ){\mathit{\boldsymbol{z}}_2} = 1 \end{array} $ | (20) |
如果让z1(p)和z2(p)成为第p次迭代的得到的解,那么,在第p+1次迭代,最优z1(p+1)和z2(p+1)能通过如下问题获得:
| $ \begin{array}{l} \quad \quad \mathit{\boldsymbol{z}}_1^{(p + 1)} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{z}}_1}} \sum\limits_{i = 1}^{{m_2}} {s_i^{(p)}({\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{z}}_1})} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{z}}_1}^{\rm{T}}(\sum\limits_{i = 1}^{{m_1}} {d_{ii}^{(p)}{\mathit{\boldsymbol{g}}_i}^{\rm{T}}{\mathit{\boldsymbol{g}}_i}} ){\mathit{\boldsymbol{z}}_1} = 1 \end{array} $ | (21) |
| $ \begin{array}{l} \quad \quad \mathit{\boldsymbol{z}}_2^{(p + 1)} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{z}}_2}} \sum\limits_{i = 1}^{{m_1}} {k_i^{(p)}({\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{z}}_2})} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{z}}_2}^{\rm{T}}(\sum\limits_{i = 1}^{{m_2}} {f_{ii}^{(p)}{\mathit{\boldsymbol{h}}_i}^{\rm{T}}{\mathit{\boldsymbol{h}}_i}} ){\mathit{\boldsymbol{z}}_2} = 1 \end{array} $ | (22) |
其中,
| $ \begin{array}{l} \quad \quad \mathit{\boldsymbol{z}}_1^{(p + 1)} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{z}}_1}} {\mathit{\boldsymbol{s}}^{{\rm{(}}p{\rm{)}}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{z}}_1}\\ {\rm{s}}{\rm{.t}}{\rm{. }}{\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{z}}_1} = 1 \end{array} $ | (23) |
| $ \begin{array}{l} \quad \quad \mathit{\boldsymbol{z}}_2^{(p + 1)} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{z}}_2}} {\mathit{\boldsymbol{k}}^{{\rm{(}}p{\rm{)}}}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{z}}_2}\\ {\rm{s}}{\rm{.t}}{\rm{. }}{\mathit{\boldsymbol{z}}_2}^{\rm{T}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{F}}^{(p)}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{z}}_2} = 1 \end{array} $ | (24) |
其中:
下面给出式(23)的紧解形式,对于问题(24),可采用同样的解过程。构建问题(23)的拉格朗日函数:
| $ L({\mathit{\boldsymbol{z}}_1},\mathit{\boldsymbol{\gamma }}) = {\mathit{\boldsymbol{s}}^{{\rm{(}}p{\rm{)}}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{z}}_1} - \frac{1}{2}\mathit{\boldsymbol{\gamma }}({\mathit{\boldsymbol{z}}_1}^{\rm{T}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{z}}_1} - 1) $ | (25) |
其中,γ是拉格朗日乘子。对L(z1, γ)求解关于z1的导数,并设置其为0,可得到问题(23)的解:
| $ \mathit{\boldsymbol{z}}_1^{(p + 1)} = \frac{1}{\mathit{\boldsymbol{\gamma }}}{({\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}})^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{s}}^{{{(p)}^{\rm{T}}}}} $ | (26) |
将该解代入等式约束z1TGTD(p)Gz1=1中,得到:
| $ \mathit{\boldsymbol{\gamma }} = \sqrt {({\mathit{\boldsymbol{s}}^{(p)}}\mathit{\boldsymbol{H}}){{({\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}})}^{ - 1}}({\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{s}}^{{{(p)}^{\rm{T}}}}})} $ | (27) |
将等式(27)代入式(26),最终有:
| $ \mathit{\boldsymbol{z}}_1^{(p + 1)} = \frac{{{{({\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}})}^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{s}}^{{{(p)}^{\rm{T}}}}}}}{{\sqrt {({\mathit{\boldsymbol{s}}^{(p)}}\mathit{\boldsymbol{H}}){{({\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{G}})}^{ - 1}}({\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{s}}^{{{(p)}^{\rm{T}}}}})} }} $ | (28) |
用相似的程序,可以计算出式(14)的解,即每次迭代计算(24),其解形式为:
| $ \mathit{\boldsymbol{z}}_2^{(p + 1)} = \frac{{{{({\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{F}}^{(p)}}\mathit{\boldsymbol{H}})}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{k}}^{{{(p)}^{\rm{T}}}}}}}{{\sqrt {({\mathit{\boldsymbol{k}}^{(p)}}\mathit{\boldsymbol{G}}){{({\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{F}}^{(p)}}\mathit{\boldsymbol{H}})}^{ - 1}}({\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{k}}^{{{(p)}^{\rm{T}}}}})} }} $ | (29) |
为了描述方便,本文定义基于上述迭代算法的L1-NPSVM为L1-NPSVM2。总的来说,L1-NPSVM2的解过程如下:
步骤1 输入数据矩阵X=[A; B],根据其计算矩阵H和G。
步骤2 初始化z1(p)和z2(p),设置p=1。
步骤3 如果两次迭代目标值的差大于0.001或迭代次数小于50,那么执行以下步骤:
1) 计算
2) 通过解问题(23)和(24),计算z1(p+1)和z2(p+1);
3) 用
步骤4 输出z1和z2。
下面来证明L1-NPSVM2迭代程序的单调递增的特性。
理论 1 L1-NPSVM2在每次迭代中具有单调递增的特性, 目标问题(13)是其单调递增目标函数。
证明 注意,每次迭代解问题(23)。定义其目标函数为J(z1)。根据式(23),从z1(p+1)的物理意义可以得到J(z1(p+1))≥J(z1(p)),即:
| $ {\mathit{\boldsymbol{s}}^{{\rm{(}}p{\rm{)}}}}\mathit{\boldsymbol{Hz}}_1^{(p + 1)} \ge {\rm{ }}{\mathit{\boldsymbol{s}}^{{\rm{(}}p{\rm{)}}}}\mathit{\boldsymbol{Hz}}_1^{(p)} $ | (30) |
其能被简化为:
| $ \begin{array}{l} \sum\limits_{i = 1}^{{m_2}} {{\rm{sign}}({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)})({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)})} \ge \sum\limits_{i = 1}^{{m_2}} {{\rm{sign}}({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)})({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)})} = \\ \quad \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} \end{array} $ | (31) |
因为
| $ \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} \ge \sum\limits_{i = 1}^{{m_2}} {{\rm{sign}}({\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p{\rm{)}}}{\rm{)}}{\mathit{\boldsymbol{h}}_i}} \mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}} $ | (32) |
组合式(31)和(32)得到:
| $ \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} \ge \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} $ | (33) |
因为对于任意两个非0变量v和u,有:
| $ \begin{array}{l} {{\rm{(}}v - u{\rm{)}}^{\rm{2}}} \ge 0 \Rightarrow {v^2} + {u^2} - 2vu \ge 0 \Rightarrow \\ \quad v - \frac{{{v^2}}}{{2u}} \le \frac{u}{2} \Rightarrow v - \frac{{{v^2}}}{{2u}} \le u - \frac{{{u^2}}}{{2u}} \end{array} $ | (34) |
令
| $ {\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}| - \frac{{{{{\rm{(}}{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}{\rm{)}}}^2}}}{{2|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|}} \le |{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}| - \frac{{{{{\rm{(}}{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}{\rm{)}}}^{\rm{2}}}}}{{2|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|}} $ | (35) |
因此,有:
| $ \begin{array}{l} \sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}|} - \sum\limits_{i = 1}^{{m_1}} {\frac{{{{{\rm{(}}{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}{\rm{)}}}^2}}}{{2|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|}}} \le \\ \quad \sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} - \sum\limits_{i = 1}^{{m_1}} {\frac{{{{{\rm{(}}{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}{\rm{)}}}^{\rm{2}}}}}{{2|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|}}} \end{array} $ | (36) |
因为,
| $ \begin{array}{l} \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} = \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} /(\mathit{\boldsymbol{z}}_1^{(p{\rm{ + }}1){\rm{T}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{(p)}}\mathit{\boldsymbol{Gz}}_1^{(p{\rm{ + }}1)}) \le \\ \quad \sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} /\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}|} \end{array} $ | (37) |
用等式
| $ \frac{{\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p + {\rm{1)}}}|} }}{{\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_i}\mathit{\boldsymbol{z}}_1^{(p + 1)}|} }} \ge \frac{{\sum\limits_{i = 1}^{{m_2}} {|{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{z}}_1^{(p)}|} }}{{\sum\limits_{i = 1}^{{m_1}} {|{\mathit{\boldsymbol{g}}_{\rm{i}}}\mathit{\boldsymbol{z}}_{\rm{1}}^{{\rm{(}}p{\rm{)}}}|} }} $ | (38) |
该不等式左右式分别为问题(13)在点z1(p+1)和z1(p)的目标值,因此,L1-NPSVM2单调增目标函数(13)。
当等式(38)成立,其意味着L1-NPSVM2可以找到一个局部最大点,此时, 认为算法收敛。在实际中,为了保证算法在有限步迭代,常规的方式是设置迭代终止条件为两次迭代目标值的差小于一个很小的值,且迭代数目应小于给定的值。在本文算法的迭代过程中,从问题(28)和(29)看到,矩阵GTD(p)G和HTF(p)H仅能保证半正定性,以至于可能得到不精确或不稳定的解。因此,我们通过正则化它来缓解此问题,即用GTD(p)G+δI和HTF(p)H+δI代替它。在执行本文算法时, δ被用作一个调节参数。容易验证,这样与GEPSVM相同,本文实际上在原目标问题(13)和(14)的分母中考虑了正则化项来保证泛化能力。对于L1-NPSVM而言,它在目标并未考虑正则化,否则算法将存在两个参数,一个正则化参数,另一个是学习率,即增加了参数的数目。L1-NPSVM实际上通过调整学习率来保证其泛化能力。显然,本文算法与L1-NPSVM同样,并未增加参数的数目,都仅包括一个参数。
3 实验验证为了验证L1-NPSVM1和L1-NPSVM2的有效性,在人工XOR数据集CompXOR和21个UCI公共数据库上进行实验。其中,CompXOR来自文献[9]。实验环境:Windows 7操作系统,CUP为Intel双核处理器3.4 GHz,内存为1 GB,运行软件为Matlab 2014。
所有比较算法都仅有一个参数:正则化参数δ属于GEPSVM和L1-NPSVM2,而学习率β属于L1-NPSVM。所有的参数通过10折交叉验证获取,且δ的搜索范围设定为{2i|i=-12, -11, …, +12}。因β需要取小值保证算法的收敛性,以至于其取值范围具有一定的限制性,为了实验公平性,其设置同文献[17],即在{0.00001, 0.00005, 0.0001, 0.0005, 0.001}范围来搜索它。因为L1-NPSVM和L1-NPSVM2是两个迭代程序,因此,需要设置它们的初始值。GEPSVM对野值或噪声具敏感性问题,以至于分类平面漂离于理想的平面,而L1-NPSVM和L1-NPSVM2可以纠正GEPSVM分类平面的漂离问题,因此,本文设置它们的初始解为GEPSVM的解。该设置也跟随了文献[18-19]的思路。对所有实验,本文记录10折交叉验证的平均分类精度,用配对T检验以克服随机性。置信水平设置为95%。当p值 < 0.05,意味着两个算法存在显著的差异。
表 1给出了GEPSVM、L1-NPSVM和L1-NPSVM2的分类结果。从表中,不难看到,所有算法中,GEPSVM的分类结果是最差的,其说明L1范数距离有助于提高分类器性能方面。当将两个基于L1范数距离的多平面分类器L1-NPSVM和L1-NPSVM2进行比较,可以看到,L1-NPSVM2远远好于L1-NPSVM,其验证了本文的迭代算法的有效性。尽管L1-NPSVM优于GEPSVM,但优势是微弱的,比如在Liver上,GEPSVM得到61.98%的精度,L1-NPSVM仅得到62.86%,而L1-NPSVM2却得到67.21%的精度。这样的结果说明,较小的学习率可能仅仅起到对解扰动的作用。计算效率上,三个算法执行得都非常快,尽管GEPSVM稍快于L1-NPSVM和L1-NPSVM2。事实上,这种现象是因为,不同于GEPSVM, L1-NPSVM和L1-NPSVM2是迭代算法且其记录的时间还包括了GEPSVM计算初始解的时间。L1-NPSVM和L1-NPSVM2在计算时间上是相当的。
| 表 1 GEPSVM, L1-NPSVM和L1-NPSVM2在原数据集上的分类性能 Table 1 Classification results of GEPSVM, L1-NPSVM, and L1-NPSVM2 on the original datasets |
为了验证L1-NPSVM2的鲁棒性,本文在包含噪声或野值的数据集上进行实验。这里,本文用高斯噪声模拟野值数据。具体地,生成满足标准正态分布的数据0.2m个,其中m为训练样本的个数,并且,标注其正类和负类样本各一半,然后,将这些数据并入训练集中。有关实验设置同第一个实验。表 2显示了GEPSVM、L1-NPSVM和L1-NPSVM2的分类精度和计算时间。从表 2中本文能得到与第一个实验相似的结论,即:GEPSVM劣于L1-NPSVM和L1-NPSVM2。当比较L1-NPSVM和L1-NPSVM2,可以看到,L1-NPSVM2远远好于L1-NPSVM。在计算效率上,L1-NPSVM和L1-NPSVM2都执行得很快;比如在大数据集Mush上,L1-NPSVM2仅仅需要约0.95 s。
| 表 2 GEPSVM, L1-NPSVM和L1-NPSVM2在向数据集引入10%高斯噪声情况下的分类性能 Table 2 Classification results of GEPSVM, L1-NPSVM, and L1-NPSVM2 on the original datasets added by 10% Gaussian noisy data |
图 1给出了L1-NPSVM2在Heart、Monk2和Cancer数据集上迭代数与目标值的关系。这里仅仅给出执行第一折且计算正类超平面时L1-NPSVM2的目标值。
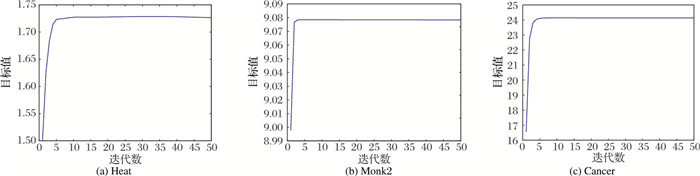
|
图 1 L1-NPSVM2在Heart、Monk2和Cancer数据集上迭代数目与目标值的关系 Figure 1 Objective values of L1-NPSVM2 versus the number of iterations on Heart, Monk2 and Cancer |
从图 1中可以看到L1-NPSVM2能快速收敛,一般能在10次迭代后收敛。
4 结语尽管L1-NPSVM模型极具简单,但如何解该模型是一个挑战的问题。在L1-NPSVM中,作者采用已有的梯度上升算法对其求解,却无法保证有效的解。本文提出一个有效的迭代算法,定义为L1-NPSVM2,其对L1-NPSVM的最大化目标问题进行求解。从理论上保证的算法存在单调性,实验结果说明了其在很小的迭代步数内收敛。在公共数据集上,结果验证了所提算法的有效性。为了公平性,跟随L1-NPSVM设计思路,本文仅仅给出L1-NPSVM2线性问题。在未来工作中,我们将对非线性L1-NPSVM2进行研究。
| [1] | SMITH R S, KITTLER J, HAMOUZ M, et al. Face recognition using angular LDA and SVM ensembles[C]//Proceedings of the 18th International Conference on Pattern Recognition. Washington, DC:IEEE Computer Society, 2006:1008-1012. |
| [2] | HSU C W, CHANG C C, LIN C J. A practical guide to support vector classification[EB/OL].[2016-11-20].http://www.csie.ntu.edu.tw/cjlin/papers/guide/guide.pdf. |
| [3] | FRANC V, SONNENBURG S. Optimized cutting plane algorithm for large-scale risk minimization[J]. Journal of Machine Learning Research, 2009, 10: 2157-2192. |
| [4] | CORTES C, VAPNIK V. Support vector networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [5] | MANGASARIAN O L, WILD E W. Multisurface proximal support vector machine classification via generalized eigenvalues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(1): 69-74. DOI:10.1109/TPAMI.2006.17 |
| [6] | GUARRACINO M R, CIFARELLI C, SEREF O, et al. A classification method based on generalized eigenvalue problems[J]. Optimization Method and Software, 2007, 22(1): 73-81. DOI:10.1080/10556780600883874 |
| [7] | JAYADEVA, KHEMCHANDANI R, CHANDRA S. Twin support vector machines for pattern classification[J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 2007, 29(5): 905-910. DOI:10.1109/TPAMI.2007.1068 |
| [8] | 杨绪兵, 陈松灿. 基于原型超平面的多类最接近支持向量机[J]. 计算机研究与发展, 2006, 43(10): 1700-1705. (YANG X B, CHEN S C. Proximal support vector machine based on prototypal multiclassfication hyperplanes[J]. Journal of Computer Research and Development, 2006, 43(10): 1700-1705.) |
| [9] | 杨绪兵, 陈松灿, 杨益民. 局部化的广义特征值最接近支持向量机[J]. 计算机学报, 2007, 30(8): 1227-1234. (YANG X B, CHEN S C, YANG Y M. Localized generalized proximal support vector machine[J]. Chinese Journal of Computers, 2007, 30(8): 1227-1234.) |
| [10] | YE Q, YE N, YIN T. Enhanced multi-weight vector projection support vector machine[J]. Pattern Recognition Letters, 2014, 42(1): 91-100. |
| [11] | SHAO Y, DENG N, CHEN W, et al. Improved generalized eigenvalue proximal support vector machine[J]. IEEE Signal Processing Letters, 2013, 20(3): 213-216. DOI:10.1109/LSP.2012.2216874 |
| [12] | SHAO Y, ZHANG C. Improvements on twin support vector machines[J]. IEEE Transactions on Neural Networks, 2011, 22(6): 962-968. DOI:10.1109/TNN.2011.2130540 |
| [13] | QI Z, TIAN Y, SHI Y. Robust twin support vector machine for pattern classification[J]. Pattern Recognition, 2013, 46(1): 305-316. DOI:10.1016/j.patcog.2012.06.019 |
| [14] | KHEMCHANDANI R, SAIGAL P, CHANDRA S. Improvements on ν-twin support vector machine[J]. Neural Networks, 2016, 79: 97-107. DOI:10.1016/j.neunet.2016.03.011 |
| [15] | YE Q, ZHAO C, YE N. Least squares twin support vector machine classification via maximum one-class with-in class variance[J]. Optimization Methods and Software, 2012, 27(1): 53-69. DOI:10.1080/10556788.2010.511667 |
| [16] | 业巧林, 赵春霞, 陈小波. 基于正则化技术的对支持向量机特征选择算法[J]. 计算机研究与发展, 2011, 48(6): 1029-1037. (YE Q L, ZHAO C X, CHEN X B. A feature selection method for TWSVM via a regularization technique[J]. Journal of Computer Research and Development, 2011, 48(6): 1029-1037.) |
| [17] | LI C, SHAO Y, DENG N. Robust L1-norm non-parallel proximal support vector machine[J]. Optimization, 2016, 65(1): 1-15. DOI:10.1080/02331934.2014.979324 |
| [18] | WANG H, LU X, HU Z, et al. Fisher discriminant analysis with L1-norm[J]. IEEE Transactions on Cybernetic, 2014, 44(6): 828-842. DOI:10.1109/TCYB.2013.2273355 |
| [19] | ZHENG W M, LIN Z C, WANG H X. L1-norm distance kernel discriminant analysis via Bayes error bound optimization for robust feature extraction[J]. IEEE Transactions on Neural Networks, 2014, 24(4): 793-805. |
| [20] | KWAK N. Principal component analysis based on L1-norm maximization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9): 1672-1680. DOI:10.1109/TPAMI.2008.114 |
| [21] | KWAK N. Principal component analysis by Lp-norm maximization[J]. IEEE Transactions on Cybernetics, 2014, 44(5): 594-609. DOI:10.1109/TCYB.2013.2262936 |




