2. 福建师范大学 数学与计算机科学学院, 福州 350117
2. School of Mathematics and Computer Science, Fujian Normal University, Fuzhou Fujian 350117, China
子空间聚类(subspace clustering)是数据挖掘诸多应用领域中一种重要工具, 它根据数据对象相似性进行无监督数据簇类划分的同时, 能够识别和生成各簇类相关的特征(或属性)集合, 组成类依赖(cluster-dependent)的子空间[1-2]。例如, 聚类由患者各种生理指标特征构成的医学诊断数据时, 子空间算法依据生理指标的差异将患者归类到不同的疾病类型, 同时输出与这些疾病相关的重要生理指标。鉴于这些实际应用数据中簇类结构的复杂性, 子空间聚类已成为聚类研究和应用中富有挑战性的任务之一[1-5]。
根据子空间搜索策略的差异, 现有子空间聚类算法大致可以分为两种类型[1]:自下而上的和自上而下的方法。前者从一维子空间出发, 根据对象投影到子空间中的密度, 迭代地搜索数据集中的稠密区域和它们的最大投影子空间;后者则从全空间出发, 为每个候选簇类计算其所在的最优子空间[3-6]。本文着重于自上而下的子空间聚类方法, 主要原因是该型方法较前者通常具有较低的时间复杂度且易于实现。实际上, 当前主要的此型算法都是以K-means[7]或K-modes[8-10]为基础的, 其基本思路是在原始算法基础上增加一个步骤以计算各属性的特征权重, 由此构造出目标簇类的软子空间(soft subspace)[3, 5]。
众所周知, K-means型算法倾向于输出大小相同和密度相同的簇类集合, 这个现象称为“均匀效应(uniform effect)”[11]。而许多实际应用产生的数据通常是不平衡的, 例如, 在前述的医学诊断数据中, 正例集(某种疾病患者)往往样本量较少, 反例集对应未患该疾病的就诊者, 样本量相对较多;此外, 正例集和反例集的“密度”(体现集合内样本间的相似性, 彼此间越相似, 则“密度”越高)通常也有很大的差异, 正例集的样本分布遵循相同的规律(即疾病模式), 具有较高的密度。受均匀效应的影响, 当前的子空间算法并不能有效聚类这样的不平衡数据(imbalanced data)[12-14]。
针对上述问题, 本文提出了“双加权(bi-weighting)”方法, 并以此为基础定义了称为BWIC (Bi-Weighting for Imbalanced data Clustering)的不平衡数据软子空间聚类算法。双加权方法赋予每个簇反映其重要性的一个权重, 称为簇权重(cluster-weight);同时赋予每个属性一个特征权重(feature-weight), 衡量属性与簇类之间的相关性。另一方面, 实际数据通常混合有数值型(numeric)和类属型 (categorical)等不同类型的属性, 而不同类属型属性的离散符号数目也可能差异很大, 导致它们对两种权重产生“不平衡”的贡献。为此, 本文另提出一种针对混合型数据的簇类权重和特征权重优化计算方法。
1 相关工作首先约定后文使用的记号。用DB表示由N个数据对象组成的待聚类数据集, 数据对象(样本)为D维向量x=(x1, x2, …, xD)T或y=(y1, y2, …, yD)T。给定聚类数K, 子空间聚类算法的目的是将N个对象划分为K个簇的集合C={c1, c2, …, ck, …, cK}, 同时确定这些簇所在的子空间, 通常用特征权重的集合W表示。这里ck表示第k个簇, 其包含的对象数记为|ck|。
若|ck|(k=1, 2, …, K)有较大差异, 则称DB为不平衡数据集。不平衡数据的聚类分析乃数据挖掘领域的一个困难问题[11-14]。现有解决方法大致可分为两类:数据预处理方法和多代表点方法, 前者基于欠采样或过采样原理对不平衡数据进行预处理, 然后再使用传统算法进行聚类[13], 后者用多个代表点表示不平衡数据中的一个簇, 即用多个划分子集表示其中的簇, 再通过凝聚操作将划分子集合并为“大”簇[14]。由于涉及采样或凝聚操作, 这些方法在实现子空间聚类方面存在困难。
现有的软子空间聚类算法大多基于特征局部加权技术[1-6], 即赋予每个簇ck的每个特征d一个权重ωkd, 其实质是定义特征加权的对象间距离度量, 进而在K-means聚类过程中学习这种度量, 也就是为每个簇ck学习得到一个优化的权重向量(ωk1, ωk2, …, ωkD)T。针对不同类型的属性, 已提出多种基于特征加权的距离度量。对于数值型属性, 对象x和y间的(平方)距离[3-4]通常定义为:
| $Di{s_{{\rm{num}}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}) = \sum\limits_{d = 1}^D {{\omega _{kd}}^\beta } \times {({x_d} - {y_d})^2},$ |
其中:β≠0为加权参数。相应地, 对于类属型数据, 通常采用如下定义[5-6]:
| $Di{s_{{\rm{cat}}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}) = \sum\limits_{d = 1}^D {{\omega _{kd}}^\beta } \times I({x_d} \ne {y_d}),$ | (1) |
其中:I (·)为指示函数, I (true)=1和I (false)=0。
为优化上述定义中的特征权重, 通常需要引入约束条件ωk1+ωk2+…+ωkD=1。显然, 在这样的归一化约束下, 特征权重分布并不能体现簇类之间的差异, 降低了它们在类不平衡数据集上的聚类性能。此外, 这些方法仅处理单一类型(数值型或类属型)的数据, 数据集同时包含两种类型的属性时, 如何平衡不同类型属性的特征权重是这些方法需要解决的共同问题之一。为此, 本文提出一种“平衡型”的新距离度量, 用于不平衡混合型数据的聚类任务。
2 BWIC聚类本章提出基于双加权机制(含簇类加权和属性加权)的不平衡数据新聚类算法BWIC, 以下首先定义属性平衡的距离度量。
2.1 属性平衡的距离度量与相关研究一样, 新距离度量也基于“朴素”假设[2]:数据集的每个属性d是统计独立的。若属性d为数值型, 假设其数值均已规范化到区间[0,1];为类属型时, 记其符号集合为Sd, 并用|Sd|表示其中的符号数。
通常, 基于划分的聚类算法(如K-means[7])旨在最小化簇内对象相对于簇“中心”的平方误差, 它衡量了簇内对象分布的分散程度(Scatter, 以下简记为Scat)。对簇ck的数值型属性d, 其平均分散度可以表示为:
| $\begin{array}{l} Sca{t_{{\rm{num}}}}({c_k},d) = \frac{1}{{|{c_k}|}}\sum\limits_{x \in {c_k}} {{{({x_d} - {{\bar x}_{kd}})}^2}} \\ \quad \quad \quad \quad \quad \,\, = \frac{1}{{2|{c_k}{|^2}}}\sum\limits_{\mathit{\boldsymbol{x}} \in {c_k}} {\sum\limits_{\mathit{\boldsymbol{y}} \in {c_k}} {{{({x_d} - {y_d})}^2}} } . \end{array}$ | (2) |
其中:xkd是簇ck在属性d上的“中心”, 数值上等于d上所有属性值的算术平均值。易知式(1) 具有如下性质:
性质1 若属性d为数值型且∀x∈ck: xd∈[0,1], 则
0≤Scatnum(ck, d)≤$\frac{1}{4}$
证明 首先, 当属性d上n个样本的取值相同时, 其分散度达到最小值0;其次, 考虑另一个极端情形, 即n/2个样本取值0, n/2个样本取值1, 均值xkd为1/2, 此时, Scatnum(ck, d)取得最大值(n/2*(0-1/2) 2)/n+n/2*(1-1/2) 2)/n=1/4。 证毕。
式(2) 第二行对分散度定义进行了变换, 其特点是不再依赖于簇“中心”, 而根据样本对之间的(平方)欧氏距离计算。由于类属型数据的样本均值没有意义[5-6, 8-10], 该变换提供了计算类属型簇类分散度的一个途径:替换式(2) 的欧氏距离为适用于类属型属性的度量, 即可导出类属型簇类分散度的计算式。基于式(1) 所示的距离度量方式, 类属型属性d上ck的分散度变换为:
| $\begin{array}{l} Sca{t_{{\rm{cat}}}}({c_k},d) = \frac{1}{{2|{c_k}{|^2}}}\sum\limits_{\mathit{\boldsymbol{x}} \in {c_k}} {\sum\limits_{\mathit{\boldsymbol{y}} \in {c_k}} {I({x_d} \ne {y_d})} } \\ \quad \quad \quad \quad \quad \,\, = \frac{1}{2}\left( {1 - \sum\limits_{s \in {S_d}} {{f_{kd}}^2(s)} } \right). \end{array}$ | (3) |
其中:
| ${f_{kd}}(s) = \frac{1}{{|{c_k}|}}\sum\limits_{x \in {c_k}} {I({x_d} = s)} $ |
表示符号s∈Sd在ck的属性d上出现的频率。式(3) 的上下界如性质2所示。
性质2 若属性d为类属型, 有
| $0 \le Sca{t_{{\rm{cat}}}}({c_k},d) \le \frac{{|{S_d}| - 1}}{{2|{S_d}|}}$ |
证明 当属性d仅含单一类别时, 根据式(3), Scatnum(ck, d)=0, 这是该属性分散度取得的最小值;相应地, 当属性d上各符号均匀分布时, Scatnum(ck, d)取得最大值, 此时, 对任意符号s有fkd(s)=1/|Sd|, 代入式(3), 分散度计算为(1-1/|Sd|*|Sd |)/2=(|Sd|-1) /|Sd|/2。
证毕。
为平衡同一个簇中不同类型属性上的分散度, 需要将Scatnum(·, ·)和Scatcat(·, ·)变换到同一数值区间。根据性质1和性质2, 若为Scatcat(·, ·)乘上平衡系数
| $\frac{{2|{S_d}|}}{{|{S_d}| - 1}} \times \frac{1}{4} = \frac{{|{S_d}|}}{{2(|{S_d}| - 1)}},$ |
则可以变换到与Scatnum(·, ·)相同的区间[0, 1/4], 由此, 定义簇ck属性d上的平均分散度为:
| $Scat({c_k},d) = \frac{1}{{|{c_k}{|^2}}}\sum\limits_{\mathit{\boldsymbol{x}} \in {c_k}} {\sum\limits_{\mathit{\boldsymbol{y}} \in {c_k}} {dis({x_d},{y_d})} } ,$ | (4) |
其中:
| $dis({x_d},{y_d}) = \left\{ {\begin{array}{*{20}{c}} {{{({x_d} - {y_d})}^2}\quad \quad \quad \quad \quad \quad 属性d为数值型}\\ \begin{array}{l} \frac{{|{S_d}|}}{{2(|{S_d}| - 1)}} \times I({x_d} \ne {y_d}),\quad \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 属性d为数值型 \end{array} \end{array}} \right.$ | (5) |
为对象x和y属性d上的平衡型(平方)距离度量。
2.2 聚类目标函数为进行软子空间聚类, 需要在式(4) 基础上定义特征加权的簇内分散度。如前所述, 在现有算法中, 每个属性d与一组特征权重ω1d, ω2d, …, ωkd, …, ωKd相关联, 但是, 受归一化条件限制, 权值并不能反映簇类间的差异。为此, 针对类不平衡数据的特点, 将这样的类依赖特征权重分解为两个独立的子权重, 即
| ${\omega _{kd}} = {h_k} \times {w_d}.$ | (6) |
其中:hk是ck的簇权重, 其数值越大表示该簇相对于其他簇愈重要;wd为属性d的全局特征权重。wd的数值衡量属性对簇类相关性程度, 满足约束条件:
| $\sum\limits_{d = 1}^D {{w_d}} = 1.$ | (7) |
这种“双加权”方法继承了全局特征加权[4]和局部特征技术[3, 5-6]的优点:一方面, 根据式(6), 每个属性d依然可以获得K个局部特征权重ω1d, ω2d, …, ωKd, 从效果上看, 这等同于局部加权技术;另一方面, 对于每个属性d本身, 它事实上只与单个权重wd相关联, 这与全局加权方法的输出是一致的, 因而可用于全局特征选择。根据上述定义, 子空间聚类算法应最小化以下目标优化函数:
| ${J_0}(C,W) = \sum\limits_{k = 1}^K {{h_k}} \sum\limits_{d = 1}^D {{w_d} \times Scat({c_k},d)} $ |
s.t.
其中:W={wd|d=1, 2, …, D}为待优化的特征权重集合。由于簇权重与特征权重无关, 这里hk(k=1, 2, …, K)并不是模型的参数, 而是通过式(8) 估计:
| ${h_k} = {\left( {\sum\limits_{d = 1}^D {Scat({c_k},d)} } \right)^{ - \frac{1}{2}}}.$ | (8) |
根据式(8), 若簇内对象彼此之间很相似(从而其簇内对象分布的平均分散度很小), 则该簇将获得较大的权重, 起到抵消K-means型算法聚类不平衡数据集时“均匀效应”的作用。
由于包含了特征权重W, J0(C, W)并不是一个凸函数。为此, 借鉴文献 [15]方法, 引入平滑函数w ln w使目标函数更容易优化。这样, BWIC算法的目标优化函数变为:
| ${J_{\rm{1}}}(C,W) = {J_0}(C,W) + \frac{1}{\gamma }\sum\limits_{d = 1}^D {{w_d}\ln {w_d}} ,$ |
这里使用了参数γ≠0控制函数的凸度。理想地, γ的取值应使得聚类结果具有最高的质量。常用聚类有效性内部指标来衡量聚类结果质量, 然而, 现有指标大多仅作用于数值型数据[16]。注意到式(5) 定义了混合型属性的对象间距离度量, 一些基于对象间距离的指标, 如著名的Silhouette指标[17], 可以容易地扩展成为混合型数据聚类的指标。具体地, 定义指标为:
| $Silhouette(C) = \frac{1}{N}\sum\limits_{x \in DB} {\frac{{OUT(\mathit{\boldsymbol{x}},C) - IN(\mathit{\boldsymbol{x}},C)}}{{\max \{ OUT(\mathit{\boldsymbol{x}},C),IN(\mathit{\boldsymbol{x}},C)\} }}} .$ | (9) |
对于x∈ck, 这里, IN (x, C)表示x与所有y∈ck(y≠x)之间的平均距离, OUT (x, C)=
给定数据集DB和K, BWIC算法需求解2.2节定义的带约束的非线性优化问题。应用拉格朗日乘子法引入式(7) 的约束条件, 算法需最小的目标函数转换为:
| $\min J(C,W)={{J}_{1}}(C,W)+\lambda \times (\sum\limits_{d=1}^{D}{{{w}_{d}}}-1)$ |
其中:λ是拉格朗日乘子。与现有的软子空间聚类算法[3-6]一样, BWIC采用一个两步骤的迭代方案求取J (C, W)的局部优解。在第一个迭代步骤中, 将C视为常数, 求解令函数J取得最小值的W。为此, 令
| ${{w}_{d}}=\frac{{{{\hat{w}}}_{d}}}{\sum\nolimits_{d=1}^{D}{{{{\hat{w}}}_{d}}}}$ | (10) |
其中
第二个迭代步骤将W视为常数, 求令J取得最小值的C, 这可以通过将每个对象x重新划分到与其最相似的簇k来实现:
| $k=\underset{j}{\mathop{\arg \max }}\,\frac{{{\theta }_{j}}}{|{{c}_{j}}|}\sum\limits_{y\in {{c}_{j}}}{\sum\limits_{d=1}^{D}{{{w}_{d}}\times Dis({{x}_{d}},{{y}_{d}})}}$ | (11) |
基于上述优化方法的聚类算法描述如下。
算法1 聚类算法BWIC。
输入 数据集DB及聚类数K、参数γ。
输出 簇集合C及权重集合H={h1, h2, …, hK}、特征权重集合W。
Begin
生成数据集初始划分C, 并初始化W中的每个属性权重为1/D。
Repeat
根据式(8) 计算各簇权重hk, k=1, 2, …, K;
固定C, 根据式(10) 更新属性权重W;
固定W, 根据式(11) 将每个对象x到划分至最相似的簇, 生成新的C。
Until J (C, W)的变化小于10-6
End
与现有K-means型软子空间聚类算法[4, 6]不同, BWIC没有使用簇“中心”概念, 是一种划分算法。算法在步骤1生成初始划分[3, 5], 首先随机选择K个对象为种子, 然后根据式(5) 计算每个对象与种子之间的距离, 将所有对象划分到最近的种子, 以此组成数据集的初始划分。在算法结构上, BWIC与K-means型聚类算法相同, 时间复杂度为O (T), 其中T是算法执行的迭代次数。
3 实验与分析本章评估BWIC在一些实际不平衡数据集上的聚类性能, 并与若干现有算法作比较。
3.1 数据集和实验设置实验使用了六个常用的UCI数据集, 如表 1所示。其中的Heart (心脏疾病数据)、Credit (澳大利亚信用卡数据)和Hypothyroid (甲状腺功能低下者数据)是混合了数值型和类属型属性的数据, 剩下的三个数据集仅包含类属型属性, 用于验证各种算法聚类复杂类型数据的性能。数据中的所有数值型属性都预先作了[0,1]规范化处理。
| 表 1 实验使用的实际数据集 Table 1 Actual datasets used in the experiments |
这些数据包含的样本都具有“不平衡”的特点, 例如, Splice数据集中的每个对象是60个核苷酸序列(位点编号从-30到+30), 分为EI、IE和Neither三组, 对象数分别为767、768和1655;Hypothyroid数据也分为三组,分别用Normal、Hyperfunction和Subnormal表示, 最大的组包含3488个样本, 最小的只有93个对象;Soybean数据中有三组包含10个样本, 但第四组有17个样本, 用D1~D4表示。其他三个数据集中的各组样本数尽管比较接近, 但具有明显的“负例”和“正例”区别, 其中, Heart数据集分为“Absence (无心脏疾病)”和“Presence (有心脏疾病)”, Mushroom分为“Edible (可食用蘑菇)”和“Poisonous (有毒蘑菇)”, 而Credit中的样本可归为“Rejected (被拒绝的申请者)”和“Approved (通过申请者)”两类。
实验使用了能聚类类属型数据的K-Modes算法(简称KM)[8]为基准算法。为对比软子空间聚类性能, 另选用了一种较新的KM改进型算法——基于互补熵的特征加权重KM算法(简称WKM)[6], 作为对比算法。使用这两种算法聚类混合型数据之前, 采用等宽离散化方法将数值型数据转换为了类属型(序数型)属性, 根据文献 [18]的建议, 离散化的“箱(bin)”数设置为$\sqrt{N}$。此外, 选用了两种能聚类混合型数据的算法为对比算法:新近提出的改进型K-原型算法(简称MKP)[16]和特征加权型K-原型算法(简称WKP)[4], 后者是一种采用全局特征加权的聚类算法, 可以输出与BWIC类似的子空间聚类结果, 其算法参数β设置为8[4], 不同类型属性间的平衡因子固定为1。所有算法都要求指定数据集的聚类数目K, 鉴于估计数据集最佳聚类数的困难[16-17], 实验将K设定为表 1所示每个数据集真实的类数。
为评价类不平衡数据集的聚类性能, 使用了两种常用于分类任务性能评价的外部准则:MacroF1和MicroF1, 前者着重结果中稀有类的评价, 而后者反映普通类的划分结果质量。二者都基于F1度量, 对于簇k, 其定义[2]为:
| $F1(k)=\frac{2\times Pr({{\pi }_{k}},{{c}_{k}})\times Re({{\pi }_{k}},{{c}_{k}})}{Pr({{\pi }_{k}},{{c}_{k}})+Re({{\pi }_{k}},{{c}_{k}})},$ |
其中:πk是数据集中与ck对应的真实类别;Pr (πk, ck)=Mk/|ck|表示πk的划分精度(precision);Re (πk, ck)=Mk/|πk|为召回率(recall),Mk是Ck和πk中共现的对象数。MacroF1和MicroF1的数值越大, 表明算法的聚类性能越好。
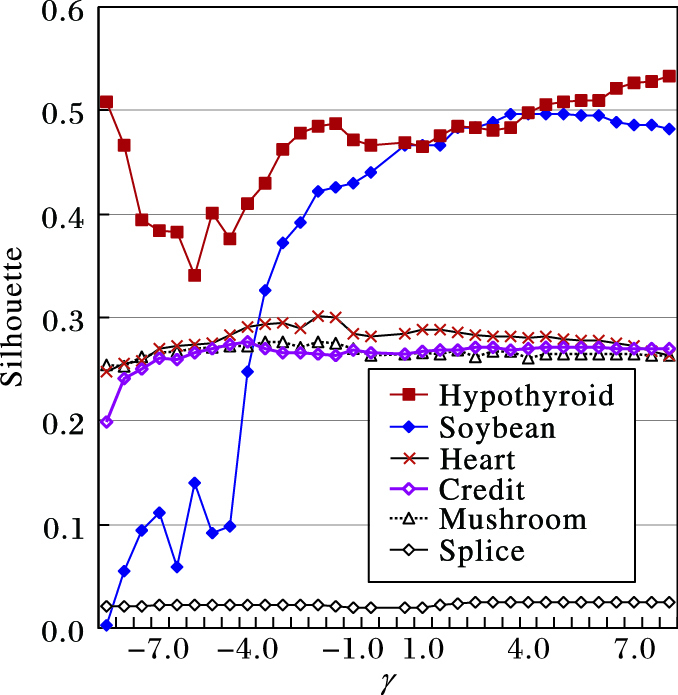
3.2 聚类结果为分析BWIC算法输出的聚类结果质量与参数γ之间的关系, 设置区间[-8,8]内不同的γ值(取增量0.5, 但不包括0), 调用BWIC算法聚类每个数据集各20次, 分别根据式(9) 计算反映结果质量的Silhouette值, 再计算平均的Silhouette值, 如图 1所示。由图 1可知, 每个数据集上对应最高聚类质量的参数值分别是γ=-2(Heart)、-3.5(Mushroom)、-4(Credit)、4.5(Splice)、8(Hypothyroid)和4.5(Soybean)。图 1还显示, 在类分布(指样本数)较为平衡的数据集上, 随γ的变化, BWIC算法的性能较为鲁棒;在Hypothyroid和Soybean这两个类样本数差异较大的数据集上, BWIC的性能受γ值影响较大, 但随着γ值的增长, 聚类质量趋于稳定。
|
图 1 六个数据集上BWIC算法参数与聚类质量间的关系 Figure 1 Relationships between the parameter of BWIC and the clustering quality on six datasets |
表 2汇总了六个数据集上不同算法的平均聚类结果。在这组实验中, 每种算法聚类各数据集100次, 计算平均MacroF1和MicroF1指标值, 并以“平均值±1标准差”的形式报告。BWIC算法的参数取图 1显示的对应最大Silhouette的γ值。为公平比较, 所有算法使用了相同的初始聚类中心(对于BWIC, 初始中心用于生成初始的数据集划分, 见算法1) 。每个数据集上最高的评价指标值使用了粗体字标注。
| 表 2 六个数据集上不同算法聚类性能比较 Table 2 Clustering performance comparison of different algorithms on six datasets |
表 2结果表明, BWIC算法在六个数据集上都取得了最好的聚类结果。由于使用了局部特征加权技术[6], WKM算法表现出比传统的KM算法更高的性能。表 2也显示, WKP算法的性能多数情况胜过MKP, 其部分原因在于WKP使用了(全局)特征加权技术[4], 可以在聚类过程中识别各属性对簇类的重要性, 进行子空间聚类。相对而言, 由于在特征加权基础上增加了簇类权重的识别功能, BWIC算法的聚类结果显得更为准确, 尤其在样本分布显著不平衡的Splice和Hypothyroid数据集上, 例如, 在Splice数据集上, BWIC算法的平均MacroF1指标和MicroF1指标都超出对比算法近50%。
3.3 权重计算结果为检验BWIC算法“双加权”方法的性能, 表 3列出了BWIC算法从每个数据集学习得到的簇类权重。如表 3所示, 输出的权重值与簇的重要性相关, 例如, 在聚类Splice数据时(其目的是识别外显子exon和内含子intron之间的边界[5]), 标识为Neither的簇因不含exon或intron, BWIC算法赋予该簇比其他两类(EI、IE)明显小的权重;在Credit数据上, 也与类似的结果, 与遭拒绝信用卡申请者(负例)的簇Rejected相比, 含正例的簇Approved的权重显得更大。
| 表 3 BWIC算法学习的簇类权重 Table 3 Cluster-weights learned by BWIC |
除簇类权重之外, BWIC算法还学习每个属性的特征权重, 表示簇类所在的软子空间。下面选择算法在Splice和Hypothyroid数据集上的聚类结果作进一步分析, 原因在于它们包含了较多的属性(Splice)或具有样本分布显著不平衡的特点(Hypothyroid), 具有代表性。图 2~3显示了BWIC算法在从这两个数据集学习到的特征权重的分布情况, 并与WKP算法的结果作相比。由于WKM算法输出类依赖的(而不是BWIC和WKP算法全局的[4])特征加权结果[6], 图 2~3未包括WKM的结果。为便于比较, 图中所示的权重均规范化到区间[0,1]。
|
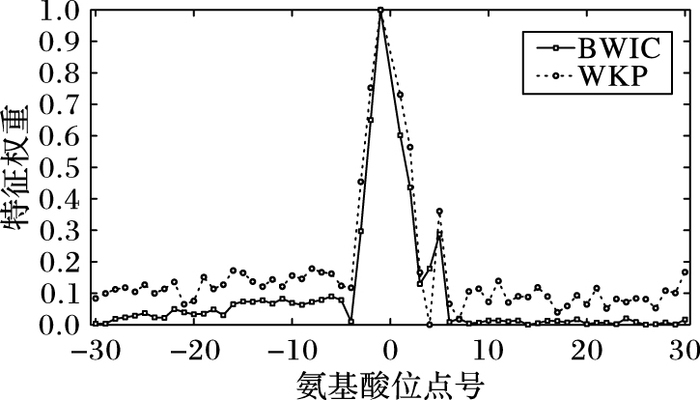
图 2 两种算法在Splice数据集上得到的特征权重分布 Figure 2 Feature-weight distributions yielded by two algorithms for dataset Splice |
从对应于Splice数据集的图 2可以看出, BWIC和WKP都赋予对应氨基酸位点-2~+2的属性较大的权重, 这些位点正好是该数据集DNA序列上“donor (供体)”和“acceptor (受体)”所处的位置[5]。但是, BWIC产生的特征权重分布更为平滑, 例如, 位点+6~+30上的特征权重并没有显著变化(实际上权重接近0), 这与WKP的结果构成了鲜明的对比。这是由于BWIC算法计算的特征权重与簇类本身的权重有关(见式(10) ), 其中Neither簇的样本占比超过50%, 且具有较小的权重(参见表 3), 削弱了这些样本对特征权重的影响, 因而BWIC可以得到平滑分布的特征加权结果。
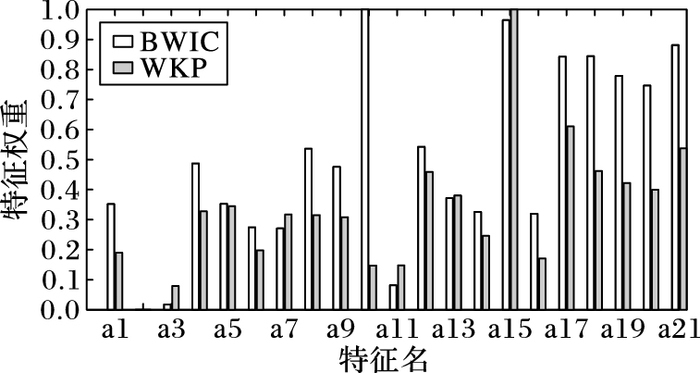
BWIC和WKP算法在Hypothyroid数据集上得到的特征权重分布也有明显差异, 如图 3所示。最明显的区别在于:BWIC算法赋予第10个和第15个属性(图 3中的a10和a15) 最高的权重, 而在WKP算法的结果中, 最高者对应a15和a17。为检验BWIC算法输出结果的合理性, 生成了两个约简数据集, 分别包含属性子集A\{a10, a15}和A\{a15, a17}, 这里A表示原始属性集合。表 4显示3种混合型数据聚类算法BWIC、WKP和MKP在两个约简数据集上的聚类性能指标值, 表中的符号↓表示指标值下降的情况。如表 4所示, 与属性集A\{a15, a17}上的聚类结果相比,三种算法在属性集A\{a10, a15}上聚类的结果中,MacroF1和MicroF1两个指标值都出现了不同程度的下降。这个结果表明, BWIC算法的“双加权”机制在进行不平衡数据子空间聚类时, 可以比对比算法获得更为准确的特征加权结果。
|
图 3 两种算法在Hypothyroid数据集上得到的特征权重分布 Figure 3 Feature-weight distributions yielded by two algorithms for dataset Hypothyroid |
| 表 4 两个约简Hypothyroid数据集上不同算法聚类性能对比 Table 4 Clustering performance comparison of different algorithms on reduced Hypothyroid datasets |
本文提出一种不平衡数据的子空间聚类新算法BWIC。与现有的软子空间聚类方法相比, 新算法基于“双加权”机制, 在优化每个属性特征权重的同时, 也优化每个簇表示其重要性的簇类权重, 二者相辅相成, 为类不平衡数据中的簇类学习最优的投影子空间。另提出了一种平衡混合型属性及具有不同符号数目的类属型属性的新距离度量, 以不同属性上样本分布的分散度为依据, 给出了属性间相异性的平衡因子。在六个常用的实际数据集上进行了实验, 实验结果表明, 相对于现有的子空间聚类算法, 本文算法在不平衡数据集上的聚类结果质量得到较为明显的改善。
后续研究工作将着重于以下两个方面:将提出的新距离度量运用到有监督分类应用中, 开展子空间最近邻分类等研究;探讨聚类有效性内部准则研究, 提供不平衡数据集最佳聚类数目估计等问题的解决方案。
| [1] | DENG Z, CHOI K-S, JIANG Y, et al. A survey on soft subspace clustering[J]. Information Sciences, 2016, 348: 84-106. DOI:10.1016/j.ins.2016.01.101 |
| [2] | AGGRAWAL C C. Data Mining: the Textbook[M]. Berlin: Springer, 2015. |
| [3] | 陈黎飞, 郭躬德, 姜青山. 自适应的软子空间聚类算法[J]. 软件学报, 2010, 21(10): 2513-2523. (CHEN L F, GUO G D, JIANG Q S. An adaptive algorithm for soft subspace clustering[J]. Journal of Software, 2010, 21(10): 2513-2523.) |
| [4] | HUANG J Z, NG M K, RONG H, LI Z. Automated variable weighting in k-means type clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 657-668. DOI:10.1109/TPAMI.2005.95 |
| [5] | CHEN L, WANG S, WANG K, et al. Soft subspace clustering of categorical data with probabilistic distance[J]. Pattern Recognition, 2016, 51(C): 322-332. |
| [6] | CAO F, JIANG J, LI D, et al. A weighting k-modes algorithm for subspace clustering of categorical data[J]. Neurocomputing, 2013, 108: 23-30. DOI:10.1016/j.neucom.2012.11.009 |
| [7] | MACQUEEN J. Some methods for classification and analysis of multivariate observation[C]//Proceedings of the 5th Berkley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press, 1967: 281-297. |
| [8] | HUANG Z, NG M. A note on k-modes clustering[J]. Journal of Classification, 2003, 20(2): 257-261. DOI:10.1007/s00357-003-0014-4 |
| [9] | 李仁侃, 叶东毅. 粗糙K-Modes聚类算法[J]. 计算机应用, 2011, 31(1): 97-100. (LI R K, YE D Y. Rough K-modes clustering algorithm[J]. Journal of Computer Applications, 2011, 31(1): 97-100.) |
| [10] | 梁吉业, 白亮, 曹付元. 基于新的距离度量的K-Modes聚类算法[J]. 计算机研究与发展, 2010, 47(10): 1749-1755. (LIANG J Y, BAI L, CAO F Y. K-Modes clustering algorithm based on a new distance measure[J]. Journal of Computer Research and Development, 2010, 47(10): 1749-1755.) |
| [11] | ZHOU K, YANG S. Exploring the uniform effect of FCM clustering: a data distribution perspective[J]. Knowledge-Based Systems, 2016, 96(C): 96-83. |
| [12] | HE H, GARCIA E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(9): 1263-1284. DOI:10.1109/TKDE.2008.239 |
| [13] | KUMAR N S, RAO K N, GOVARDHAN A, et al. Undersampled K-means approach for handling imbalanced distributed data[J]. Progress in Artificial Intelligence, 2014, 3(1): 29-38. DOI:10.1007/s13748-014-0045-6 |
| [14] | LIANG J, BAI L, DANG C, et al. The k-means-type algorithms versus imbalanced data distributions[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(4): 728-745. DOI:10.1109/TFUZZ.2011.2182354 |
| [15] | DE AMORIM R C. A survey on feature weighting based k-means algorithms[J]. Journal of Classification, 2016, 33(2): 210-242. DOI:10.1007/s00357-016-9208-4 |
| [16] | LIANG J, ZHAO X, LI D, et al. Determining the number of clusters using information entropy for mixed data[J]. Pattern Recognition, 2012, 45(6): 2251-2265. DOI:10.1016/j.patcog.2011.12.017 |
| [17] | ROUSSEEUW P J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis[J]. Computational and Applied Mathematics, 1987, 20: 53-65. DOI:10.1016/0377-0427(87)90125-7 |
| [18] | YANG Y, WEBB G I, Proportional k-interval discretization for naive-Bayes classifiers[C]//Proceedings of the 12th European Conference on Machine Learning. Berlin: Springer, 2001: 564-575. |




