2. 东南大学 计算机科学与工程学院, 南京 211189
2. School of Computer Science and Engineering, Southeast University, Nanjing Jiangsu 211189, China
离群点检测(Outlier Detection)作为数据挖掘技术的重要研究领域之一, 是从大量事物中发现少量与多数事物具有明显区别的异常个体的过程[1]。离群点检测在很多领域有着广泛的应用前景,例如, 电子商务中的欺诈行为、金融领域中信用卡恶意透支、网络安全中的恶意攻击、地震预报中的异常波形、网络入侵抵御等。
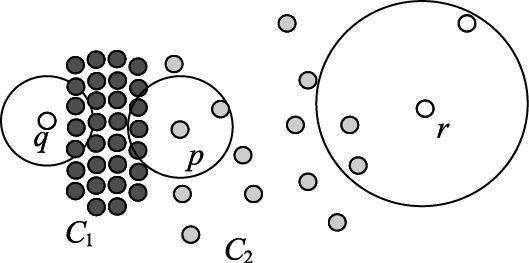
离群点检测技术由于其独特的知识发现功能而得到了较深入的研究。近年来提出了一系列检测方法, Johnson等[2]提出基于深度的算法, Knorr等[3]提出基于距离的算法FindAllOutsD, Breunig等[4]提出带离群度的离群点检测算法LOF (Local Outlier Factor), Papadimitirou等[5-13]提出LOCI (LOcal Correlation Integral)算法等。局部离群点检测是离群点检测的一个重要研究方向, 文献 [11]针对LOF算法的不足, 提出了基于反向k近邻(Reverse k Nearest Neighbors, RkNN)的局部离群度判别方法INFLO (INFLuenced Outlierness), 不同于LOF算法只考虑数据点的k近邻, 算法同时考虑数据点的反向k近邻对数据点离群度的影响, 从而避免数据分布异常情况下LOF算法可能出现的错判。例如, 图 1中, 根据LOF算法对数据点离群度的定义, 可能出现属于聚类C2的数据点p的离群度高于数据点q和r的离群度, 出现p比数据点q和r更易被判定为离群点的错判现象。采用INFLO方法后, 在分析p、q、r的k近邻(k-Nearest Neighbors, KNN) 的同时, 进一步分析各个数据点反向k近邻。INFLO方法结合数据点p的反向k近邻数据点对p的影响, 可以得出p的离群度小于q和r的离群度的正确结果。
|
图 1 数局分布异常情况 Figure 1 Abnormal data distribution |
INFLO方法可以解决LOF算法不适应数据分布异常情况下离群点判定的缺陷, 但仍然存在以下不足:
1) 算法既要查询生成每个数据点p的k近邻, 又要查询p的反向k近邻(RkNN), 频繁的RkNN查询对算法的性能影响很大, 尽管文献 [11]中采用R树等索引结构来提高查询效率, 但并不能从根本上解决效率问题;另一方面, 当数据集维度较高时, R树等索引结构的效率比顺序遍历查询还要差, 也无法实现其提高效率的目的。
2) 算法需要对每一个数据点的离群度进行分析计算, 判断其是否可能是离群点, 导致时间开销很大, 大量反向k近邻查询加剧了这种负担;实际数据集中, 异常分布点仅占数据集的很小部分, 例如图 1中, 只有聚类C1和C2的边缘点, 以及诸如q和r这样的数据点分布异常, 对数据集中的大多数数据点(C1和C2中的数据点)无需分析其RkNN, 就可以得出正确的离群判断。
针对上述问题, 本文提出一种基于局部密度的快速离群点检测方法LDBO (Local Density Based Outlier detection), 算法无需对数据集中所有数据点进行离群与否分析, 在仅需对部分数据点计算反向k近邻的情况下, 有效地解决数据分布异常环境下离群点检测问题。
1 相关工作 1.1 LOF算法基于密度的离群点检测算法LOF[4], 提出基于密度的数据点离群度计算方法, 主要定义如下:
定义1[4] ε-邻域和数据点p的k-距离。p为数据集D中数据点, ε为距离参数值, k为自然数, d为欧氏距离函数:
1) p的ε-邻域Nε(p)={ x∈D | d (p, x)≤ε}。
2) 数据点p的k-距离k-dist (p)定义为p与距其第k近的数据点的距离, p的k-邻域简写为Nk(p), Nk(p)={x∈D|d (p, x)≤k-dist (p)}。
ε-邻域用于确定数据点的密度特征比较范围, 即每个数据点的密度特征与其ε-邻域内的数据点比较。
定义2[4] p的核心距离。p为数据集D中数据点, ε为距离参数值, MinPts为给定自然数, p的核心距离定义如下:
core-distanceε,MinPts(p) =
| $\left\{ \begin{array}{*{35}{l}} 不作定义, & |{{N}_{\varepsilon }}(p) <MinPts| \\ MinPts\text{-}dist(p), & 其他 \\ \end{array} \right.$ |
即当p的ε-邻域内数据点数目大于MinPts时, p的核心距离定义为p的MinPts-距离。
定义3[4] p关于o的可达距离。p与o为D中数据点, p∈Nε(o), 则p关于o的可达距离定义为:
reachability-distanceε, MinPts(p, o)=
| $\left\{ \begin{array}{*{35}{l}} 不作定义, \ \ \ \ |{{N}_{\varepsilon }}(o) <MinPts| \\ \max \{core-dis\tan c{{e}_{\varepsilon ,MinPts}}(o),d(o,p)\},\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 其他 & {} \\ \end{array} \right.$ |
定义4[4] p的局部可达密度。p为D中数据点, 参数定义如上, p的局部可达密度定义为:
lrdMinPts(p)=
| ${{\left( \tfrac{\sum\limits_{o\in {{N}_{MinPts}}(p)}{reachability}}{|{{N}_{MinPts}}(p)|}-\tfrac{\sum\limits_{o\in {{N}_{MinPts}}(p)}{dis\tan c{{e}_{\infty ,MinPts}}(p,o)}}{|{{N}_{MinPts}}(p)|} \right)}^{-1}}$ |
p的局部可达密度表征了p的局部密度, 值越大, p所代表的局部区域越稠密。
定义5[4] p的离群因子。p为D中数据点, p的离群因子定义如下:
| $O{{F}_{MinPts}}\left( p \right)=\tfrac{1}{|{{N}_{MinPts}}(p)|}\sum\limits_{o\in {{N}_{MinPts}}(p)}{\frac{lr{{d}_{MinPts}}(o)}{lr{{d}_{MinPts}}(p)}}$ |
p的离群因子定义为p的k-邻域内数据点与p点局部可达密度的平均比值, 数据点的离群因子值越高, 说明p点与其邻域内数据点密度特征差异越显著, 其成为离群点的可能性也就越大。
分析图 1中p、q、r的数据分布特征发现, 由于q较p更靠近聚类C1, 因而q的局部密度高于p, 而p与q的k近邻点集均由分布均匀的C1中数据点构成, 得出p的离群因子高于q的错误判断;对r与p也可进行类似分析, 发现LOF方法对数据分布异常情况下数据点的离群因子确实存在错判的可能。
1.2 INFLO算法在LOF方法的基础上, 文献 [11]提出了新的判定数据点离群因子的方法, 相关定义如下:
定义6[11] p的反向k近邻。p的反向k近邻定义如下:RNNk(p)={q|q∈D, p∈NNk(q)}。
定义7[11] p的局部密度。den (p)=1/k-dist (p)。
定义8[11] p的离群影响因子INFLOk(p)。p的离群影响因子INFLOk(p)定义如下:
| $INFL{{O}_{k}}\left( p \right)=\tfrac{de{{n}_{avg}}(I{{S}_{k}}(p))}{den(p)}$ |
其中:
ISk(p)=NNk(p)∪RNNk(p)
| $de{{n}_{\rm avg}}\left( I{{S}_{k}}\left( p \right) \right)=\frac{1}{|I{{S}_{k}}(p)|}\sum\limits_{o\in I{{S}_{k}}(p)}{den(o)}$ |
相对于LOF算法, INFLO算法既考虑数据点的k近邻, 又兼顾数据点的反向k近邻, 可以更好地表征数据点所在区域的密度特征。
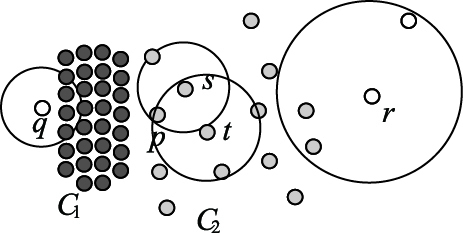
重新分析图 2所示数据分布异常的情况可以发现, 考虑了反向k近邻后, p的离群因子明显小于q与r的离群因子, 符合数据实际分布情况。
|
图 2 反向k近邻分析实例 Figure 2 Example of reverse k nearest neighbors analysis |
尽管INFLO算法通过引入反向k近邻有效地解决了数据分布异常情况下的离群点检测问题。但对每个数据点计算反向k近邻使得算法的时间消耗激增。考虑现实世界, 分布异常的数据通常只占数据集的一小部分, 大多数数据点都属于正常模式(非离群点), 大量数据点无需反向k近邻计算即可进行离群判别。
因此, 考虑基于INFLO算法, 从数据点密度特征角度研究数据点与其邻域内数据的离群关系, 设计判断策略, 在不影响INFLO算法判段正确性的前提下, 尽可能减少需进行反向k近邻分析的数据点规模, 提升离群分析效率。
2.2 局部密度聚类与离群判定聚类分析和离群点检测有着密切联系, LOF算法和INFLO算法均借助密度聚类的重要概念k近邻距离来衡量数据集中各个数据点是否为离群点。而实际数据集中离群点所占的比例很小, 占数据集主体的各个聚簇内的大多数数据点都不属于离群点, 但是为了避免离群点检测中“拒真”(false negative)现象的出现(即漏判聚簇内部可能存在的离群点), LOF算法和INFLO算法都要对各个聚簇内部的数据点进行逐一判断, 严重影响了基于密度的离群点检测算法效率。
为了解决这一问题, 引入下述定义:
定义9 核心影响点集(Kernel Infection Set, KIS)。p为数据集D中数据点, p的核心影响点集称KISk(p)={o|o∈NNk(p)∧p∈NNk(o)}。
定义10 强k近邻点(strong k nearest neighbors)和弱k近邻点(weak k nearest neighbors)。p∈D, 若满足
由定义可知, 若p为强k近邻点, 意味着p的k近邻内至少占比不小于μ的数据点的k近邻也包含p, 即p的k近邻内有较大比例μ的数据点周围区域的密度分布趋于p周围数据密度分布。满足μ>0, 则图 1中的p、q、r点不可能为强k近邻点。
定义11 局部核心点。若p∈D, 且
| $k-dist\left( p \right)\le \frac{1}{|N{{N}_{k}}(p)|}\sum\limits_{o\in N{{N}_{k}}(p)}{k-dist(o)}$ |
称p为局部核心点。p的k近邻距离不大于其k近邻内数据点k近邻距离的均值, 说明p的k近邻内数据点总体上向p收敛, p的局部密度高于其k近邻数据点的平均密度。
性质1 若p为局部核心点, p一定不是离群点。
证明 从局部密度聚类角度考虑, p的k近邻距离不大于其k近邻内数据点k近邻距离的均值, 说明p邻域内数据点总体上向p聚集, p对应聚簇的核心点, 以p为起点遍历其密度相连数据点, 可以生成一个聚簇;同时, p邻域内不可能出现类似图 1的数据分布异常现象, 无需考虑其反向k近邻数据点的形象, 根据LOF算法离群因子定义和局部核心点的定义易得p的离群因子小于1。从这两方面分析, p都不符合离群点的特征, p不是离群点。 证毕。
性质2 p为局部核心点, 且p为强k近邻点, 若q∈KISk(p), 且k-dist (q)≤k-dist (p), 则q也是局部核心点。
证明 由性质1, p为局部核心点不是离群点, 有如下关系:
| $k-dist\left( p \right)\le \tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(p)}{k-dist(o)}}{|N{{N}_{k}}(p)|}$ |
| $\begin{align} & \tfrac{k-dist(q)}{|N{{N}_{k}}(p)|}+\tfrac{\sum\limits_{o\in N{{N}_{k}}(p)\wedge o\in N{{N}_{k}}(q)}{k-dist(o)}}{|N{{N}_{k}}(p)|}+ \\ & \tfrac{\sum\limits_{o\in N{{N}_{k}}(p)\wedge o\notin N{{N}_{k(q)}}}{k-dist(o)}}{|N{{N}_{k}}(p)|} \\ \end{align}$ | (1) |
数据点q的k近邻内点的k近邻距离均值为:
| $\begin{align} & avg\left( q \right)=\tfrac{\sum\limits_{o\in N{{N}_{k}}(q)}{k-dist(o)}}{|N{{N}_{k}}(q)|}= \\ & \quad \quad \quad \quad \tfrac{k-dist(p)}{|N{{N}_{k}}(q)|}+\tfrac{\sum\limits_{o\in N{{N}_{k}}(q)\wedge o\in N{{N}_{k}}(p)}{k-dist(o)}}{|N{{N}_{k}}(q)|}+ \\ & \quad \quad \quad \quad \tfrac{\sum\limits_{o\in N{{N}_{k}}(q)\wedge o\notin N{{N}_{k}}(p)}{k-dist(o)}}{|N{{N}_{k}}(q)|} \\ \end{align}$ |
由式(1) 有:
avg (q)≥
| $\begin{align} & \tfrac{|N{{N}_{k}}(p)|*k-dist(p)+k-dist(p)-k-dist(q)}{|N{{N}_{k}}(q)|}\text{-} \\ & \tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(p)\wedge o\in N{{N}_{k}}(q)}{k-dist(o)}}{|N{{N}_{k}}(q)|}+\tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(q)\wedge o\notin N{{N}_{k}}(p)}{k-dist(o)}}{|N{{N}_{k}}(q)|} \\ \end{align}$ |
由于k-dist (q)≤k-dist (p), 有
| $ avg\left( q \right)\ge \tfrac{|N{{N}_{k}}(p)|*k-dist(q)}{|N{{N}_{k}}(q)|}\text{-} \\ \quad \quad \quad \tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(p)\wedge o\in N{{N}_{k}}(q)}{k-dist(o)}}{|N{{N}_{k}}(q)|}+ \tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(q)\wedge o\notin N{{N}_{k}}(p)}{k-dist(o)}}{|N{{N}_{k}}(q)|} \\ $ |
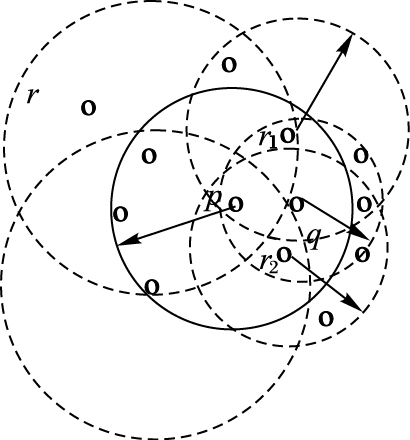
对分子部分的两个求和表达式进行分析, 对o∈KISk(p), 即同时属于点q和点p的k近邻点集的数据点。分析可知, 这类数据点的数目很少, 因为在q的k近邻内, p不可能与q很靠近, 这些点又位于q的k近邻内, 将导致p的k近邻点集中较多的数据点位于以p、q连线为直径方向的球状区域(如图 3中r1和r2) 。而题设中有p为强k近邻点, 故而可知p的k近邻内数据点总体上密度分布与p相近;且k-dist (p)小于其k近邻内数据点k近邻距离均值, 若p的k近邻点集内较多数据点位于q的k近邻点集, 将很难同时满足这两点。有进一步分析可知, 即便p的k近邻内有极少的数据点o在q的k近邻内, k-dist (o)≤dist (o, q)+k-dist (q)。例如图示k=5时, 有2个数据点属于KISk(p), 同时p为强k近邻点, 则p显然不满足局部核心点的条件。
|
图 3 数据分布示意图 Figure 3 Data distribution schematic example |
对于满足o∉NNk(p)∧o∈NNk(q)条件的这类数据点一定存在, 否则p的k近邻点集中的部分数据点和p点将构成q的k近邻点集, 这将导致p为局部核心点和p为强k近邻点两个条件的无法同时满足;并且这类数据点与可能存在的o∈NNk(p)∧o∈NNk(q)的数据点同属q的k近邻, 其k近邻距离相近。
通过上述分析可知,
| $\begin{matrix} \sum\nolimits\limits_{o\in N{{N}_{k}}(q)\wedge o\notin N{{N}_{k}}(p)}{k-dist(o)}-\sum\nolimits\limits_{o\in N{{N}_{k}}(p)\wedge o\in N{{N}_{k}}(q)}{k-dist(o)\ge } \\ \eta >0 \\ \end{matrix}$ |
| $avg\left( q \right)\ge \tfrac{|N{{N}_{k}}(p)|*k-dist(q)+\eta }{|N{{N}_{k}}(q)|}$ |
近似可得k-dist (q)≤
q为局部核心点。 证毕。
引入局部离群度定义如下:
定义12 局部离群因子(LOCal Outlierness, LOCO)。若p∈D, 0<μ≤1, p的局部离群因子为LOCOk(p)。
| $LOC{{O}_{k}}\left( p \right)=\left\{ \begin{matrix} \tfrac{\sum\nolimits\limits_{o\in N{{N}_{k}}(p)}{\tfrac{k-dist(p)}{k-dist(o)}}}{|N{{N}_{k}}(p)|} & \tfrac{|KI{{S}_{k}}(p)|}{|N{{N}_{k}}(p)|}>\mu \\ \tfrac{\sum\nolimits\limits_{o\in I{{S}_{k}}(p)}{\tfrac{k-dist(p)}{k-dist(o)}}}{|I{{S}_{k}}(p)|} & 其他 \\ \end{matrix} \right.$ |
通过引入强k近邻点和弱k近邻点, 若p为强k近邻点, 由强近邻点定义知, 此时p的邻域内不可能出现类似图 1的数据分布异常情况, 故而无需考虑p的反向k近邻内点对p离群判断的影响;若p为弱k近邻点, 则p的邻域内可能存在数据分布异常现象, 此时对p的离群性判定需进一步考虑其反向k近邻的影响。
2.3 数据点离群判断策略根据定义10, 将数据点划分成两类——强k近邻点集和弱k近邻点集。若p为强k近邻点, 说明p的k近邻内一定数量的数据与p的数据分布相近, 不存在图 1所示异常的情况;否则, 说明p的k近邻内数据点可能存在分布异常的情况, 容易验证图 1中的p、q、r显然属于弱k近邻点。对这两类数据点, 分别采用不同的策略进行处理。
1) 强k近邻点的离群判别。
若p为强k近邻点, 说明其k近邻内超过100×μ%(0.5≤μ≤1) 的数据分布与p相近, 不存在数据分布异常情况, 对p的离群判断, 不需要考虑其反向k近邻的影响。
进一步判断p是否为局部核心点, 若p不是局部核心点, 则LOCOk(p)>1, 可能为离群点, 若LOCOk(p)>t (假设t为所设离群因子阈值), 则p为离群点;若p为局部核心点, 由性质1得p不是离群点, 进一步分析其k近邻内数据点。
若p为局部核心点, 可以将p的k近邻内数据点分为三类:
① o∈NNk(p)-KISk(p)。
这一类数据点的k近邻不包含p, 对应局部密度高于p的区域, 从密度聚类角度分析, 与p可能属于同一聚簇也可能属于不同聚簇, 其离群性与p没有直接关系, 尽管其局部密度高于非离群点p的局部密度, 但并不意味这类数据点一定都不是离群点, 仍需进一步分析其局部k近邻内数据分布情况以判断这类数据点是否为离群点。
② o∈KISk(p), 且k-dist (o)≤k-dist (p)。
由性质1和性质2, o不是离群点。
③ o∈KISk(p), 且k-dist (o)>k-dist (p)。
这类数据点同样属于p的强影响点集, 与情况②的区别是这些点可能不是局部核心点, 因而有成为离群点的可能, 必须进一步分析其k近邻数据点的分布情况, 以确定是否为离群点。从而, 当判断出强k近邻点p非离群点的同时, 可以根据性质2将p的k近邻点集中k近邻距离小于等于p的点标注为非离群点。
2) 弱k近邻点的离群判别。
p为弱k近邻点, 说明|
这样, 通过强k近邻点与弱k近邻点的定义, 可以将数据集中数据点划分为无需考虑反向k近邻直接进行离群判断和需要考虑反向k近邻进行离群判断两类。数据集中的绝大多数数据点属于前者, 从而无需对每个数据点分析计算其反向k近邻数据点的影响, 避免了频繁分析计算反向k近邻对算法效率的影响;另一方面, 对占数据集比重较大的强k近邻点, 通过性质2, 可以对其k近邻内的部分待判定数据点进行预判断, 减少待判定数据点的数量, 提高离群点检测算法的效率。
2.4 LDBO算法算法 LDBO。
输入 维数据集D、k; 离群因子阈值t。
输出 数据集D的离群点集合Outlier。
Initialization;
For each x in D {
If (x not be marked as outlier or non-outlier){
GenNNK (x, D, k);
L=NNk(x);
For (i=1; i≤|L|; i++){
Generate (L[i], D, k);
If x∈NNk(L[i]){insert L[i] into KISk(x)}
}
If (|KISk(x)|/NNk(x)≥μ){ // x为强k近邻点
GenMKDist (L, D, k); //计算x的邻域点k-Dist均值
If (x is local core){
x is marked as non-outlier;
For (i=1; i≤|L|; i++){
If (k-Dist (L[i])≤k-Dist (x))
x is marked as non-outlier;
}
}
else
{ If (LOCOk(x)≤t) x is marked as non-outlier;
Else {x is marked an outlier;}
}
}
else //x为弱k近邻点
{ generate RNNk(x);
If (LOCOk(x)>t){x is marked an outlier;}
Else{x is marked as non-outlier;}
}
}
}
3 实验分析本章对所提出的LDBO算法进行性能测试。考虑LDBO算法主要基于INFLO算法[11]进行改进, 在保持其离群检测效果的同时提升检测效率;如文献 [12]指出, INFLO算法[11]至今仍然属于基于局部密度的离群检测算法中效果最好的算法之一。因此, 考虑只对LDBO算法与LOF算法、INFLO算法进行实验分析。
实验环境配置如下:Intel 1.8 GHz/512 MB, Windows 2000 Server, 所用代码均用VC++ 6.0实现。实验所使用的数据共两种:第一种来源于网络入侵检测数据集 KDD-CUP 99, 该数据集中的数据对象分为五大类, 包括正常的连接、各种入侵和攻击等。为了进行实验, 分别选取1000条记录和10000条记录的两个数据集(分别称为KDD-CUP-1000和KDD-CUP-10000), 并对数据进行适当修改, 使得攻击(即离群点)占数据集的3%, 对非数值属性维进行数值化处理。第二种是仿真数据集(Synthetic DataSet), 包括2200条数据记录, 维度为2。精度采用以下量度对算法进行评价:
| $Precision=\frac{判断正确的离群点数目}{检测出的离群点总数}$ |
检测出的离群点总数指算法在数据集上运行后,判定为离群点的数据点数目;判断正确的离群点数目指算法判定为离群点的数据点中真实离群点的数目。
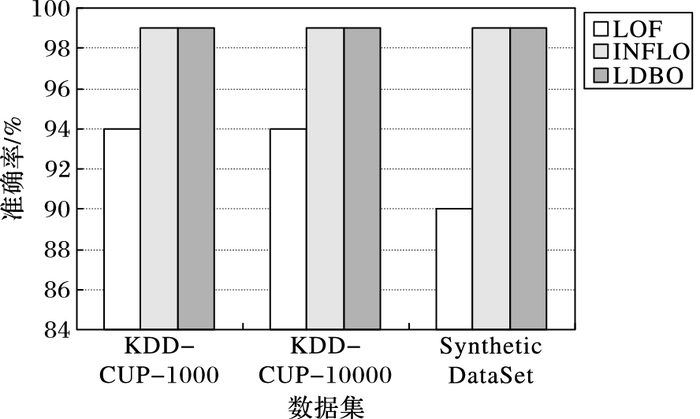
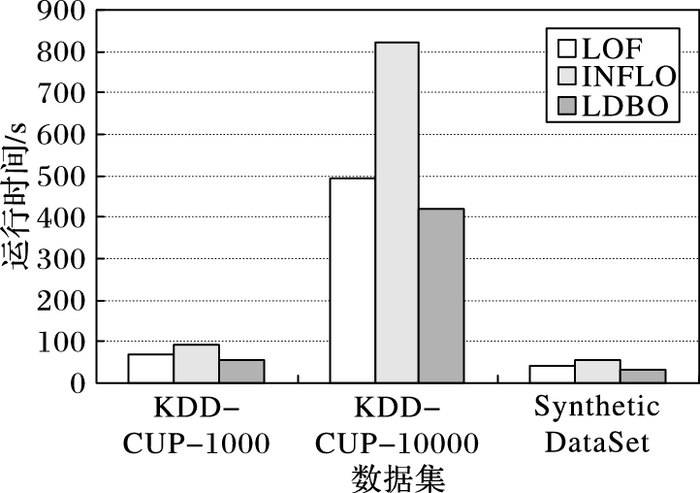
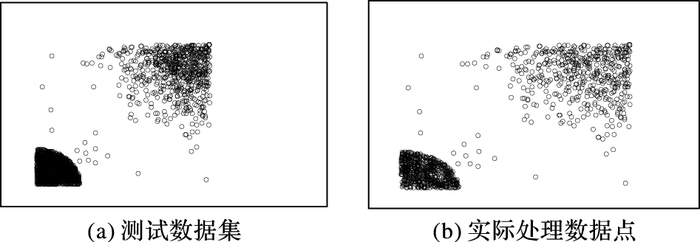
图 4~5对应k=5, μ=0.5, t=1.2时, LOF算法、INFLO算法和LDBO算法在两类实验数据集上的运行情况。实验结果表明, LDBO算法与INFLO算法对两类数据集的离群点检测精度相似, 而基于LOF的离群点检测算法检测精度相对较低, 特别是对仿真数据集, 其离群点检测精度远低于LDBO算法和INFLO算法;由图 5可知, LDBO算法效率明显优于另两种算法, 这符合第2章理论分析。LDBO算法通过定义强k近邻点和弱k近邻点对数据点进行区分处理, 有效地避免了INFLO算法对所有数据点进行反向k近邻计算分析的不足;进一步, 通过性质2, 对待检测数据点进行预判断, 从而在保证检测精度的前提下, 有效地提高了占数据集较大比重的聚簇内数据点的离群点检测效率。仿真测试数据集分布情况如图 6(a)所示,数据集包含两个大的聚簇, 中间区域存在类似图 1的数据分布异常情况。图 6(b)对应LDBO算法在仿真数据集上运行时, 利用性质2进行预判断后, 实际需要分析离群因子判断是否为离群点的数据点, 与图 6(a)对比发现两个聚簇内部相当部分的数据点可以根据性质2进行预判断, 无需作进一步的分析处理。
|
图 4 不同算法的精度对比 Figure 4 Precision of different algorithms |
|
图 5 不同算法的执行时间对比 Figure 5 Running time comparison of different algorithms |
|
图 6 测试数据集与LDBO算法实际处理数据对比 Figure 6 Comparison of test data and actual processed data by LDBO algorithm |
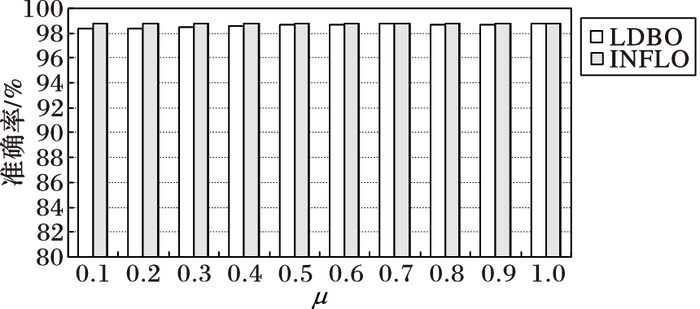
进一步分析强k近邻点和弱k近邻点参数μ对算法性能的影响, 采用仿真数据集, μ∈[0.1, 1], k=5, t=1.2, 对算法LDBO和基于INFLO的算法进行实验, 实验结果如图 7~8所示。LDBO算法中, 参数μ设置将影响对强近邻点和弱近邻点的判定, 例如, μ值设置得比较低, 则数据集中大部分数据点都将被判定为强k近邻点, 但这并不影响对数据集中数据点离群判定的准确性, 只要μ的取值不为0, 都可以有效避免图 1所示数据分布极端情况对离群点判定的影响, 即使某个k近邻内数据点分布稀疏,甚至离群点的数据点被判作强k近邻点, 按照LDBO算法思想, 仍需进一步分析其是否为局部核心点以确定其离群与否, 图 8验证了μ的取值与算法精度无关这一点。而当μ设置得很高时, 则成为强k近邻点的数据点规模越来越小, 则LDBO算法对数据点进行离群预判定的作用发挥得就较少, 大多数数据点都被当作弱k近邻点需要分析其反向k近邻以判定其离群性。由图 7可以清楚地发现这一现象, 当μ大于0.6后, 随着μ的增加, LDBO算法与基于INFLO算法的时间消耗差渐渐减小。

|
图 7 不同μ值算法执行时间对比 Figure 7 Runing time comparison with different μ |
|
图 8 不同μ值算法的精度比较 Figure 8 Precision comparison with different μ |
本文研究了基于局部密度的离群点的检测问题, 提出了LDBO算法。算法通过引入强k近邻点和弱k近邻点有效地解决了存在异常数据分布的数据集离群点检测问题, 将需要借助反向k近邻点分析以判断离群性的数据点限定在较小范围内, 进一步提出相关性质, 实现对数据集中非离群点的预判定, 有效提高了基于密度离群点检测算法的效率和对数据集的适应性。
| [1] | HAWKINS D. Identification of Outliers[M]. London: Chapman and Hall, 1980: 1-45. |
| [2] | JOHNSON T, KWOK I, NG R. Fast computation of 2-dimensional depth contours[C]//KDD 1998: Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining. Menlo Park: AAAI Press, 1998: 224-228. |
| [3] | KNORR E M, NG R T. Algorithms for mining distance-based outliers in large datasets[C]//VLDB 1998: Proceedings of the 24rd International Conference on Very Large Data Bases. San Francisco: Morgan Kaufmann Publishers, 1998: 392-403. |
| [4] | BREUNIG M M, KRIEGEL H-P, NG R T, et al. LOF: identifying density-based local outliers[J]. ACM SIGMOD Record, 2000, 29(2): 93-104. DOI:10.1145/335191 |
| [5] | PAPADIMITRIOU S, KITAGAWA H, GIBBONS P B. LOCI: fast outlier detection using the local correlation integral[C]//Proceedings of the 19th International Conference on Data Engineering. Piscataway, NJ: IEEE, 2004: 315-326. |
| [6] | AGGARWAL C, YU P. Outlier detection for high dimensional data[J]. ACM SIGMOD Record, 2001, 30(2): 37-46. DOI:10.1145/376284 |
| [7] | 倪巍伟, 陈耿, 陆介平, 等. 基于局部信息熵的加权子空间离群点检测算法[J]. 计算机研究与发展, 2008, 45(7): 1189-1194. (NI W W, CHEN G, LU J P, et al. Local entropy based weighted subspace outlier mining algorithm[J]. Journal of Computer Research and Development, 2008, 45(7): 1189-1194.) |
| [8] | 刘露, 左万利, 彭涛. 异质网中基于张量表示的动态离群点检测方法[J]. 计算机研究与发展, 2016, 53(8): 1729-1739. (LIU L, ZUO W L, PENG T. Tensor representation based dynamic outlier detection method in heterogeneous network[J]. Journal of Computer Research and Development, 2016, 53(8): 1729-1739. DOI:10.7544/issn1000-1239.2016.20160178) |
| [9] | 黄添强, 余养强, 郭躬德, 等. 半监督的移动对象离群轨迹检测算法[J]. 计算机研究与发展, 2011, 48(11): 2074-2082. (HUANG T Q, YU Y Q, GUO G D, et al. Trajectory outlier detection based on semi-supervised technology[J]. Journal of Computer Research and Development, 2011, 48(11): 2074-2082.) |
| [10] | 胡彩平, 秦小麟. 一种基于密度的局部离群点检测算法DLOF[J]. 计算机研究与发展, 2010, 47(12): 2110-2116. (HU C P, QIN X L. A density-based local outlier detecting algorithm[J]. Journal o f Computer Research and Development, 2010, 47(12): 2110-2116.) |
| [11] | JIN W, TUNG A K H, HAN J, et al. Ranking outliers using symmetric neighborhood relationship[C]//Proceedings of the 10th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin: Springer, 2006: 577-593. |
| [12] | RADOVANOVIC M, NANOPOULOS A, IVANOVIC M. Reverse nearest neighbors in unsupervised distance-based outlier detection[J]. IEEE Transactions on Knowledge & Data Engineering, 2014, 27(5): 1369-1382. |
| [13] | 杨慧, 王丽婧. 基于聚类和拟合的QAR数据离群点检测算法[J]. 计算机工程与设计, 2015, 36(1): 174-177. (YANG H, WANG L J. QAR data outlier detection algorithm based on clustering and fitting[J]. Computer Engineering and Design, 2015, 36(1): 174-177.) |




