近几年来,随着社交媒体的兴起以及互联网技术的发展,图像数据产生了爆炸性的增长。图像视觉特征与高层语义之间“语义鸿沟”的存在成为了图像检索领域发展的瓶颈。因此,如何有效地表示图像的视觉特征是提高图像内容的利用效率、缩小语义鸿沟的核心问题。图像特征表示是指利用统计学习的方法(也常称为维数约简)将样本从输入空间(底层视觉特征)线性或者非线性地映射到一个低维空间,从而获得关于原数据集一个比较紧致的低维表示。一般情况下,都会用向量来表示图像数据,即向量中的元素表示图像样本的特征,将其按照逐行或者逐列的顺序拉伸成为一个向量来表示图像数据。但是,该方法常常因其维数过高导致计算呈指数增长从而造成“维数灾难”[1]。为了解决图像数据表示中存在的“维数灾难”问题,人们提出了若干维数约简的方法。典型的维数约简算法主要包括主成分分析[2]、线性判别分析[3]、独立分量分析[4]、奇异值分解[5]、非负矩阵分解(Non-negative Matrix Factorization, NMF)[6]及流形学习[7]等。其中,NMF算法与其他维数约简方法不同,它的独特之处在于矩阵分解过程中施加了非负约束,即在矩阵分解过程中所有元素都是非负的。NMF将原始矩阵分解为左右两个非负矩阵的乘积,称左侧的矩阵为基矩阵,右侧的矩阵称为系数矩阵。因此,可以将原始矩阵的列向量用基矩阵中列向量的加权和来表示,这里的权重系数就是系数矩阵。这种向量组合具有直观的语义解释,符合人类思维中“局部构成整体”的概念[8]。由于非负约束的引入使得NMF具有良好的纯加性和数据描述性,从而使其更加贴近应用领域。
NMF算法自提出后得到了学术界的广泛关注和深入研究,并获得了大量的研究成果。为了提高NMF算法的有效性,满足一定的需求并且达到期待的效果,大量学者在NMF框架中引入了各种约束,比如稀疏性、流形、正交性和判别性等,提出了若干种改进的NMF算法,并被成功地应用到各个领域,取得了良好的实验效果。Cai等[7]将流形学习与NMF相结合提出了图正则化非负矩阵分解(Graph Regularized Nonnegative Matrix Factorization,GNMF)算法,该算法考虑了原始数据中蕴含的几何结构,使得低维表示很好地保留了原始数据样本的近邻结构;但是由于它没有考虑数据集中的已知标签信息,同时其稀疏性也不是很理想,因而限制了GNMF算法的应用。Liu等[9]提出一种半监督约束非负矩阵分解(Constrained Nonnegative Matrix Factorization,CNMF)算法,该算法将已知标签信息约束到NMF分解中,缺陷是没有考虑样本的几何结构以及未施加稀疏约束。后来,胡学考等[10]在CNMF的基础之上增加了稀疏约束,提出了基于稀疏约束的半监督非负矩阵分解(Constrained Nonnegative Matrix Factorization with Sparseness,CNMFS),该方法不仅考虑标签信息,还对基矩阵进行了稀疏约束,实验结果表明该算法的聚类精度高;但CNMFS算法并没有考虑到原始数据所隐藏的几何信息,因此限制了其应用范围。随后,姜小燕等[11]提出了基于图正则化和稀疏约束的半监督非负矩阵分解(Graph-regularized and Constrained Nonnegative Matrix Factorization with Sparseness,GCNMFS)算法,该算法在保持数据几何结构的同时还利用已知样本的标签信息进行半监督学习,并且对基矩阵施加稀疏约束,使分解后的人脸图像有更高的识别率。以上算法均存在一定的不足,即单一的图像特征并不能够很好地描述图像的内容,所以不少学者提出了基于特征融合的NMF算法[12-14],实验结果表明这些算法相对于传统的维数约简方法有更好的效果。
本文通过深入分析基于NMF的图像特征表示原理,探讨如何通过综合多种约束增强NMF的特征表示能力以及如何通过融合具有不同稀疏度的特征来提高部件的学习能力,提出了基于特征融合的多约束非负矩阵分解(Multi-Constraint Nonnegative Matrix Factorization based on Feature Fusion, MCNMFFF)的图像分类算法,将非负矩阵分解用于图像分类问题,最终获得具有稀疏性和判别性的图像低维特征,提高图像分类的准确率。本文的主要工作在于:1) 在NMF框架中同时施加先验约束、稀疏约束和图正则化,提高基矩阵的稀疏度,增强系数矩阵的鉴别能力。本文提出的MCNMFFF算法能够较好地揭示图像内在的局部几何特征。2) 目前现存的基于特征融合的NMF方法均是将全局和局部等特征或形状和颜色等特征进行融合,忽略了基矩阵的稀疏度,若基矩阵的稀疏度增加则学习部件的能力也会相应地提高,所以稀疏性对NMF是至关重要的。本文将NMF分解后的具有不同稀疏度的图像特征进行了融合,解决了单一种类的图像特征不能很好地描述所有不同语义图像视觉内容的问题,从而有效地提高了图像的表示能力和聚类性能。3) 给出了MCNMFFF算法的迭代更新公式,并证明了该算法的收敛性;同时,在两个常用数据集上进行了聚类实验,实验结果验证了MCNMFFF算法的有效性。
1 非负矩阵分解对矩阵进行分解时,得到的结果并不一定是唯一解。同样,矩阵进行NMF时往往也是不尽相同的。对于给定的n个非负样本xi(i=1, 2, …, n), 每一个xi∈Rm都是m维的列向量,组成矩阵X=[x1, x2, …, xn]∈Rm×n。NMF算法的目的就是寻找两个非负矩阵U∈Rm×k和V∈Rn×k(k≤mn/(m+n)),使得X≈UVT, 也就是使X与UVT的差异值最小,即优化目标函数。其中,U是基矩阵,V是系数矩阵,并且U和V中的元素都是非负的。NMF算法可用欧氏距离来描述目标函数:
| $\begin{array}{l} {O_F} = \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^T}} \right\|_{\rm{F}}^2\\ {\rm{s}}{\rm{.t}}.\quad \mathit{\boldsymbol{U}} \ge 0,\mathit{\boldsymbol{V}} \ge 0 \end{array}$ | (1) |
其中:‖‖F是矩阵的Frobenius范数。式(1) 是通过求解分解前后两个矩阵元素差的平方来衡量X与UVT的相似度,其值越小,则说明X与UVT的相似度越高,即分解前后的矩阵距离越小;反之越大。
上述目标函数在对U和V同时求解时并不是凸函数,只有在单独对U或者V求解时才是凸函数,且能得到最优解。利用最速下降法和迭代法推导出目标函数(1) 的乘性迭代更新公式如下:
| ${u_{ik}} \leftarrow {u_{ik}}\frac{{{{\left( {\mathit{\boldsymbol{XV}}} \right)}_{ik}}}}{{{{\left( {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}} \right)}_{ik}}}}$ | (2) |
| ${v_{jk}} \leftarrow {v_{jk}}\frac{{{{\left( {{\mathit{\boldsymbol{X}}^T}\mathit{\boldsymbol{U}}} \right)}_{jk}}}}{{{{\left( {\mathit{\boldsymbol{V}}{\mathit{\boldsymbol{U}}^T}\mathit{\boldsymbol{U}}} \right)}_{jk}}}}$ | (3) |
其中:U=[uik], V=[vjk]。经过推导证明,目标函数(1) 在迭代更新规则下是收敛的,文献[6]证明了NMF算法的收敛性。
2 基于特征融合的多约束非负矩阵分解 2.1 相关算法GNMF算法在进行矩阵分解的同时,要求在低维空间中继续保持样本的几何结构,也就是要求分解后的数据保持原始数据固有的结构信息。GNMF假设两个数据点xi和xj在原始空间是邻近点,那么在新基下相应的vi和vj也是邻近点。
设G为原始数据点构成的图,其中Rij表示权重矩阵,Np(xi)表示xi的p个近邻,当xi或者xj属于Np(xi), 则Rij为1;否则为0。定义L=D-S, D是对角矩阵,L是拉普拉斯矩阵。GNMF算法的最小化目标函数为:
| $\begin{array}{l} {{O}_{\rm{F}}} = \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^T}} \right\|_{\rm{F}}^2 + \lambda {\rm{Tr}}\left( {{\mathit{\boldsymbol{V}}^T}\mathit{\boldsymbol{LV}}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\mathit{\boldsymbol{U}} \ge 0,\mathit{\boldsymbol{V}} \ge 0 \end{array}$ | (4) |
CNMFS在进行矩阵分解的同时不仅将已知标签信息约束到NMF分解中,还对基矩阵进行了稀疏化。CNMFS算法的最小化目标函数为:
| $\begin{array}{l} {O_{\rm{F}}} = \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{Z}}^T}{\mathit{\boldsymbol{A}}^T}} \right\|_{\rm{F}}^2 + \beta \left\| \mathit{\boldsymbol{U}} \right\|_{\rm{F}}^2\\ {\rm{s}}{\rm{.t}}{\rm{.}}\mathit{\boldsymbol{U}} \ge 0,\mathit{\boldsymbol{Z}} \ge 0 \end{array}$ | (5) |
GCNMFS综合了GNMF和CNMFS算法的优点,在保留数据蕴含的几何结构的同时利用样本的标签信息进行半监督学习,并且对基矩阵施加稀疏性的约束。GCNMFS算法的最小化目标函数为:
| $\begin{array}{l} {O_{\rm{F}}} = \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right\|_{\rm{F}}^2 + \lambda {\rm{Tr}}\left( {{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{LAZ}}} \right) + \beta \left\| \mathit{\boldsymbol{U}} \right\|_{\rm{F}}^2\\ {\rm{s}}{\rm{.t}}{\rm{.}}\quad \mathit{\boldsymbol{U}} \ge 0,\mathit{\boldsymbol{Z}} \ge 0 \end{array}$ | (6) |
针对目前改进的NMF算法的优缺点,同时考虑到单一种类的特征不可能对所有不同语义的图像视觉内容都能获得满意的描述结果,本文将多种约束引入NMF算法中,并将NMF分解的具有不同稀疏度的图像特征进行融合,提出了MCNMFFF算法。首先,分别用CNMFS和GNMF模型在NMF算法中加入先验约束、稀疏约束和图正则化,这样不仅能够充分利用已知标签信息来提高算法的鉴别能力,还能够在低维的数据空间保持样本的几何结构,同时还可以提高基图像的稀疏度;其次,将CNMFS和GNMF分解的具有不同稀疏度的图像特征进行融合,从而解决单一种类的特征不能够很好描述所有不同语义图像视觉内容的问题,进一步提高部件的学习能力;最后,将以上两个部分整合到一个目标函数中,用数学理论进行推导证明来描述本文算法。本文提出的MCNMFFF算法的目标函数如下:
| $\begin{array}{l} {O_{\rm{F}}} = \theta \left[ {\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_{\rm{1}}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right\|_{\rm{F}}^2 + \beta \left\| {{\mathit{\boldsymbol{U}}_{\rm{1}}}} \right\|_{\rm{F}}^2} \right] + \\ \quad \quad \quad \left( {1 - \theta } \right)\left[ {\left\| {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_{\rm{2}}}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right\|_{\rm{F}}^2 + \lambda {\rm{Tr}}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{LV}}} \right)} \right]\\ {\rm{s}}{\rm{.t}}{\rm{.}}\quad {\mathit{\boldsymbol{U}}_{\rm{1}}} \ge 0,\mathit{\boldsymbol{Z}} \ge 0,{\mathit{\boldsymbol{U}}_{\rm{2}}} \ge 0,\mathit{\boldsymbol{V}} \ge 0 \end{array}$ | (7) |
其中:参数θ∈(0, 1) 是融合系数;参数β∈(0, 1) 为稀疏系数, 为了使优化求解过程变得稳定、快速,这里用Frobenius范数来约束稀疏项;λ≥0为正则化参数;U1是经CNMFS分解后得到的基矩阵,U2是经GNMF分解后得到的基矩阵;A是标签约束矩阵,Z是辅助矩阵,且系数矩阵V=AZ。
MCNMFFF算法的目标函数与GCNMFS算法的目标函数略微不同:GCNMFS是将图正则化和稀疏约束引入到NMF模型中与重构误差作为一个整体来表示GCNMFS的目标函数;而MCNMFFF算法是将NMF模型分解后的具有不同稀疏度的图像特征进行融合,该图像特征由GNMF模型分解特征的和CNMFS模型分解的特征两部分组成,所以MCNMFFF的目标函数主要是用两个模型目标函数的加权来表示,其中每一部分均包含重构误差和正则项。
2.3 MCNMFF迭代更新规则由式(7) 可知,目标函数单独对于变量U1、Z、U2和V而言是凸函数,但是同时对于四个变量而言则是非凸函数,所以找到全局的最优解是非常困难的。针对这一问题,本文采用最速下降法和迭代法来推导目标函数(7) 的乘性迭代更新规则来寻找局部最优解。
通过代数运算,目标函数(7) 可以重写为:
| $\begin{array}{l} {O_{\rm{F}}} = \theta {\rm{Tr}}\left( {\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right){{\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)}^{\rm{T}}}} \right) + \\ \mathit{\boldsymbol{\theta \beta }}\left\| {{\mathit{\boldsymbol{U}}_1}} \right\|_{\rm{F}}^2 + \left( {1 - \mathit{\boldsymbol{\theta }}} \right){\rm{Tr}}\left( {\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right){{\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right)}^{\rm{T}}}} \right) + \\ \left( {1 - \mathit{\boldsymbol{\theta }}} \right)\lambda {\rm{Tr}}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{LV}}} \right) = \theta {\rm{Tr}}\left( {\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}} \right) - 2\theta {\rm{Tr}}\left( {\mathit{\boldsymbol{XAZU}}_1^{\rm{T}}} \right) + \\ \theta {\rm{Tr}}\left( {{\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}} \right) + \theta \beta \left\| {{\mathit{\boldsymbol{U}}_1}} \right\|_{\rm{F}}^2 + \left( {1 - \theta } \right){\rm{Tr}}\left( {\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}} \right) - \\ 2\left( {1 - \theta } \right){\rm{Tr}}\left( {\mathit{\boldsymbol{XVU}}_2^{\rm{T}}} \right) + \left( {1 - \theta } \right){\rm{Tr}}\left( {{\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{VU}}_2^{\rm{T}}} \right) + \\ \left( {1 - \theta } \right)\lambda {\rm{Tr}}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{LV}}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\mathit{\boldsymbol{U}}_1} \ge 0,\mathit{\boldsymbol{Z}} \ge 0,{\mathit{\boldsymbol{U}}_2} \ge 0,\mathit{\boldsymbol{V}} \ge 0 \end{array}$ |
定义拉格朗日乘子δ、ε、φ和ρ, 分别约束u1、z、u2和v。则由拉格朗日定理可得拉格朗日函数为:
| $L = {O_{\rm{F}}} + {\rm{Tr}}\left( {\delta \mathit{\boldsymbol{U}}_1^{\rm{T}}} \right) + {\rm{Tr}}\left( {\varepsilon {\mathit{\boldsymbol{Z}}^{\rm{T}}}} \right) + {\rm{Tr}}\left( {\varphi \mathit{\boldsymbol{U}}_2^{\rm{T}}} \right) + {\rm{Tr}}\left( {\rho {\mathit{\boldsymbol{V}}^{\rm{T}}}} \right)$ | (8) |
1) 更新变量U1。
将拉格朗日函数(8) 对变量U1求偏导数,同时令偏导数为零,可得:
| $\frac{{\partial L}}{{\partial {\mathit{\boldsymbol{U}}_1}}} = - 2\theta \mathit{\boldsymbol{XAZ}} + 2\theta {\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZ}} + 2\theta \mathit{\boldsymbol{\beta }}{\mathit{\boldsymbol{U}}_1} + \delta = 0$ | (9) |
通过利用KKT(Karush-Kuhn-Tucker)条件δiju1ij=0, 可将式(9) 化简为:
| $ - \left( {\mathit{\boldsymbol{XAZ}}} \right){u_1} + \left( {{\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZ}}} \right){u_1} + \mathit{\boldsymbol{\beta }}{\mathit{\boldsymbol{U}}_1}{u_1} = 0$ | (10) |
根据式(10) 可以进一步得到变量U1的迭代更新规则:
| ${u_{1ij}} \leftarrow {u_{1ij}}\frac{{{{\left( {\mathit{\boldsymbol{XAZ}}} \right)}_{ij}}}}{{{{\left( {{\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZ}} + \mathit{\boldsymbol{\beta }}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}$ | (11) |
2) 更新变量Z。
将拉格朗日函数(8) 对变量Z求偏导数,同时令偏导数为0,可得:
| $\frac{{\partial L}}{{\partial \mathit{\boldsymbol{Z}}}} = - 2\theta {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_1} + 2\theta {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1} + \varepsilon = 0$ | (12) |
通过利用KKT条件εijzij=0, 可将式(12) 化简为:
| ${\rm{ - }}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_1}} \right)z + \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)z = 0$ | (13) |
根据式(13) 可以进一步得到变量Z的迭代更新规则:
| ${z_{ij}} \leftarrow {z_{ij}}\frac{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}$ | (14) |
3) 更新变量U2。
将拉格朗日函数(8) 对变量U2求偏导数,同时令偏导数为零,可得:
| $\frac{{\partial L}}{{\partial {\mathit{\boldsymbol{U}}_2}}} = - 2\left( {1 - \theta } \right)\mathit{\boldsymbol{XV}} + 2\left( {1 - \theta } \right){\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} + \varphi = 0$ | (15) |
通过利用KKT条件φiju2ij=0, 可将式(15) 化简为:
| ${\rm{ - }}\left( {\mathit{\boldsymbol{XV}}} \right){u_2} + \left( {{\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}} \right){u_2} = 0$ | (16) |
根据式(16) 可以进一步得到变量U2的迭代更新规则:
| ${u_2}_{ij} \leftarrow {u_2}_{ij}\frac{{{{\left( {\mathit{\boldsymbol{XV}}} \right)}_{ij}}}}{{{{\left( {{\mathit{\boldsymbol{U}}_2}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}} \right)}_{ij}}}}$ | (17) |
4) 更新变量V。
将拉格朗日函数(8) 对变量V求偏导数,同时令偏导数为零,可得:
| $\begin{array}{l} \frac{{\partial L}}{{\partial \mathit{\boldsymbol{V}}}} = - 2\left( {1 - \theta } \right){\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_2} + 2\left( {1 - \theta } \right)\mathit{\boldsymbol{VU}}_2^{\rm{T}}{\mathit{\boldsymbol{U}}_2} + \\ \quad \quad 2\left( {1 - \theta } \right)\mathit{\lambda }\mathit{\boldsymbol{LV}} + \rho = 0 \end{array}$ | (18) |
通过利用KKT条件ρijvij=0, 可将式(18) 化简为:
| ${\rm{ - }}\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_2}} \right)v + \left( {\mathit{\boldsymbol{VU}}_2^{\rm{T}}{\mathit{\boldsymbol{U}}_2}} \right)v + \lambda \mathit{\boldsymbol{DV}}v - \lambda \mathit{\boldsymbol{WV}}v = 0$ | (19) |
根据式(19) 可以进一步得到变量V的迭代更新规则:
| ${v_{ij}} \leftarrow {v_{ij}}\frac{{{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_2} + \lambda \mathit{\boldsymbol{WV}}} \right)}_{ij}}}}{{{{\left( {\mathit{\boldsymbol{VU}}_2^{\rm{T}}{\mathit{\boldsymbol{U}}_2} + \lambda \mathit{\boldsymbol{DV}}} \right)}_{ij}}}}$ | (20) |
对于乘性更新规则式(11)、(14)、(17) 和(20),得出以下理论。
定理1 对于U1≥0、Z≥0、U2≥0和V≥0, 目标函数(7) 在式(11)、(14)、(17) 和(20) 的更新规则下是收敛的,即非增。
为了证明定理1,首先定义辅助函数。
定义1 若函数G(u, u′)是函数F(u)的辅助函数,则满足G(u, u′)≥F(u), 且G(u, u)=F(u)。
引理1 若函数G(u, ut)是函数F(u)的辅助函数,那么函数F(u)在以下更新规则下是非增的:
| ${u^{t + 1}} = \mathop {{\rm{arg}}\;{\rm{min}}}\limits_u G\left( {u,{u^t}} \right)$ | (21) |
证明 很明显, 当u=ut时函数G(u, ut)取得最小值。由定义1可知,G(ut+1, ut)′≥F(ut+1)可表示为:
| $F\left( {{u^{t + 1}}} \right)\mathop \le \limits^{{\rm{def}}} G\left( {{u^{t + 1}},{u^t}} \right)\mathop \le \limits^{{\rm{min}}} G\left( {{u^t},{u^t}} \right)\mathop \le \limits^{{\rm{def}}} F\left( {{u^t}} \right)$ |
从中可看出,当ut为G(u, ut)的局部极小值时才有F(ut+1)=F(ut)。如果函数F(u)存在导数,并且在ut的一个微小邻域内连续,则有∇F(ut)=0。
由式(21) 可以得到收敛到局部极小值点umin的序列:
| $F\left( {{u_{\min }}} \right) \le \cdots \le F\left( {{u^{t + 1}}} \right) \le F\left( {{u^t}} \right) \le \cdots \le F\left( {{u^1}} \right) \le F\left( {{u^0}} \right)$ |
所以,通过定义辅助函数G(u, ut), 可以使目标函数(7) 的迭代规则满足式(21)。证毕。
需要证明更新规则(14) 和式(21) 是一致的。为此,用FZij表示目标函数中仅与Z中任一元素zij有关的部分,于是得到:
| $\begin{array}{l} {F_{{Z_{ij}}}}\left( {{z_{ij}}} \right) = {\left( { - 2\theta \mathit{\boldsymbol{XAZU}}_1^{\rm{T}} + \theta {\mathit{\boldsymbol{U}}_1}{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}} \right)_{ij}}\\ {F_{{Z_{ij}}}}^\mathit{'}\left( {{z_{ij}}} \right) = {\left( { - 2\theta {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{U}}_1} + 2\theta {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)_{ij}}\\ {F_{{Z_{ij}}}}^{\mathit{''}}\left( {{z_{ij}}} \right) = 2\theta {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)_{ii}}{\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)_{jj}} \end{array}$ |
其中,FZij′(zij)和FZij″(zij)分别表示函数FZij对变量zij的一阶偏导数和二阶偏导数。
引理2 定义目标函数中关于变量zij的辅助函数如下:
| $\begin{array}{l} G\left( {z,z_{ij}^t} \right) = {F_{{Z_{ij}}}}\left( {z_{ij}^t} \right) + {F_{{Z_{ij}}}}^\prime \left( {z_{ij}^t} \right)\left( {z - z_{ij}^t} \right) + \\ \begin{array}{*{20}{c}} {}&{}&{\frac{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}{{z_{ij}^t}}} \end{array}{\left( {z - z_{ij}^t} \right)^2} \end{array}$ | (22) |
证明 很明显,G(z, z)=FZij(z), 根据辅助函数的定义可知,只需证明G(z, zijt)≥FZij(zij)即可。
FZij(zij)的泰勒级数展开式如下:
| $\begin{array}{l} {F_{{Z_{ij}}}}\left( {{z_{ij}}} \right) = {F_{{Z_{ij}}}}\left( {z_{ij}^t} \right) + {F_{{Z_{ij}}}}^\mathit{'}\left( {z_{ij}^t} \right)\left( {z - z_{ij}^t} \right) + \\ \begin{array}{*{20}{c}} {}&{}&{\frac{1}{2}} \end{array}{F_{{Z_{ij}}}}^{\mathit{''}}\left( {z_{ij}^t} \right){\left( {z - z_{ij}^t} \right)^2} = {F_{{Z_{ij}}}}\left( {z_{ij}^t} \right) + \\ \begin{array}{*{20}{c}} {}&{}&{{F_{{Z_{ij}}}}^\mathit{'}\left( {z_{ij}^t} \right)\left( {z - z_{ij}^t} \right)} \end{array} + \\ \begin{array}{*{20}{c}} {}&{}&{\theta \left[ {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)}_{ii}}{{\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{jj}}} \right]} \end{array}{\left( {z - z_{ij}^t} \right)^2} \end{array}$ | (23) |
比较式(22) ~(23),不难发现不等式G(z, zijt)≥FZij(zij)与不等式(24) 是等价的:
| $\frac{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}{{z_{ij}^t}} \ge \theta {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)_{ii}}{\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)_{jj}}$ | (24) |
根据线性代数可得如下不等式:
| $\begin{array}{l} \left( {{\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{AZU}}_1^T{\mathit{\boldsymbol{U}}_1}} \right) = \sum\limits_l {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZ}}} \right)\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)} \\ \ge \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZ}}} \right)\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right) \ge \sum\limits_l {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right){z^t}\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right)} \\ \ge {z^t}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)\left( {\mathit{\boldsymbol{U}}_1^{\rm{T}}{\mathit{\boldsymbol{U}}_1}} \right) \end{array}$ | (25) |
又因0<θ<1, 所以由不等式(25) 和参数θ可知不等式(24) 成立,从而G(z, zijt)≥FZij(zij)成立, 于是引理2获证。证毕。
最后证明定理1的收敛性。
证明 用辅助函数(22) 代替式(21) 中的G(u, ut), 可以得到以下更新规则:
| $z_{ij}^{\left( {t + 1} \right)} = z_{ij}^{\left( t \right)} - z_{ij}^{\left( t \right)}\frac{{{F_{{Z_{ij}}}}^\prime \left( {z_{ij}^{\left( t \right)}} \right)}}{{2\theta {{\left( {{\mathit{\boldsymbol{A}}^{\bf{T}}}\mathit{\boldsymbol{AZU}}_1^{\bf{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}} = z_{ij}^{\left( t \right)}\frac{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\bf{T}}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}{{{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AZU}}_1^{\bf{T}}{\mathit{\boldsymbol{U}}_1}} \right)}_{ij}}}}$ |
因为式(22) 是函数的辅助函数,因此,采用当前规则更新是非递增的。同时,目标函数(7) 具有下界。综上所述,定理1的收敛性获证。证毕。
由于目标函数(7) 中的U1和Z是对称的,U2和V也是对称的,所以在U1、U2和V的迭代更新规则下同样可用相似的证明过程来证明定理1。
3 实验与分析 3.1 数据集及参数选择常用的人脸图像和物体的数据集有Yale-32[15]、ORL、COIL20和PIE-pose27等,由于本文算法在几个数据集上的实验效果大致相同,所以在实验中为了展示MCNMFF算法的有效性以及减少程序运行时间,选择在Yale-32和COIL20两个具有代表性的常用物体和人脸数据库上进行验证实验。Yale-32数据集包含15名志愿者的面部表情图像,因为所取表情不同所以每个人有11幅表情不一的图像,每个志愿者的姿态表情包括:微笑、大笑、严肃、生气等;面部是否有饰物等。该数据集共有165幅图片。COIL20数据集包含20个不同的物体(玩具小鸭、招财猫、杯子等),其中,每个物体在水平面上每隔5°拍摄一张图片,因此每个物体一共有72幅图片,整个数据集共计1 440幅图片。
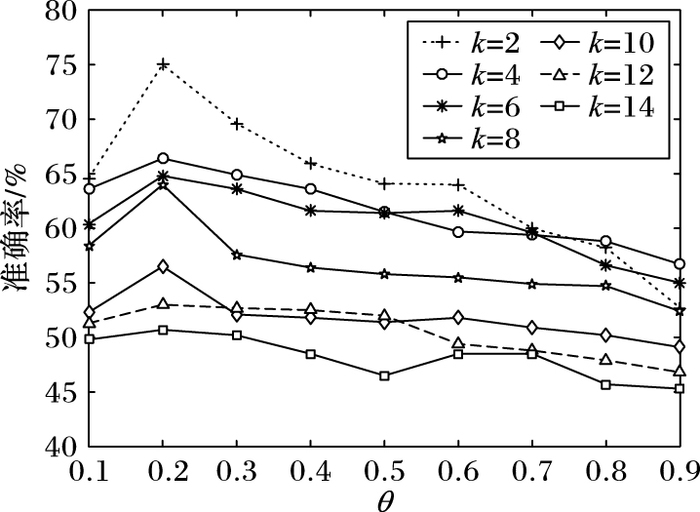
MCNMFFF模型有三个关键的参数:融合系数θ、稀疏系数β和正则化参数λ。目标函数中的融合系数θ通常是由实验的结果来决定的,一般说来,不同数据集对应的最佳融合系数值也不同。图 1给出了Yale-32数据集在取不同k值的情况下不同θ值对应的准确率。
|
图 1 θ值对准确率的影响曲线 Figure 1 Influence curve of θ value on accuracy |
从图 1中θ值与类别数k和准确率(Accuracy,AC)的关系曲线可以看出:在θ=[0.1, 0.2]时,AC是随着θ值的增大而增大的;在θ=(0.2, 0.9]时,AC的大致趋势是随着θ值的增大而减小;因此,θ的最佳取值为0.2。由于GNMF、CNMFS目标函数中不包含融合系数θ, 所以准确率不会受到θ的影响,但是GNMF、CNMFS的准确率会受到类别数k的影响,大致趋势是随着类别数k的增加呈下降趋势,尽管有时会因实验环境等因素出现一定的波动,即图 1中的趋势与GNMF、CNMFS等并不是一致的。
此处之所以没有给出融合系数在COIL20数据集上对准确率的影响曲线图,是因为在该数据集上θ对不同类别数k的准确率影响不大,所以COIL20数据集与Yale-32数据集的θ值取值相同。
同样地,稀疏系数β和正则化参数λ也是由实验结果确定的。在实验中,如果β值过大则会使得图像过于稀疏以至于不能很好地表示图像。经过不断的实验,选取β=0.3。通过对实验结果的分析可知,当λ从10到1 000变化时,MCNMFFF算法对AC和归一化互信息(Normalized Mutual Information, NMI)的影响不太大。所以,根据实验的经验选取λ=100。在本文实验中,将选取每类样本中的前20%作为标记样本,剩余的作为未标记样本,并从其中随机地选择k类样本进行聚类实验,每个k值运行20次取平均值作为最后的结果。由于各参数的选取对目标函数的收敛速度并没有明显的影响,基本上在迭代50次以内就已经收敛得非常好了,所以考虑到程序的运行时间,设置最大迭代次数为200。
3.2 实验与分析实验中用准确率(AC)[16]和归一化互信息(NMI)[17]两个评价指标来验证MCNMFFF在Yale-32和COIL20两个数据集上的聚类性能。所以,需要在矩阵分解和特征融合后对低维数据进行聚类,然后根据聚类结果来分析数据的表示性能。
为了证明MCNMFFF算法的有效性,将NMF算法、GNMF算法、CNMFS算法和GCNMFS算法作为聚类实验的对比对象。为了使实验结果具有说服性,对每个k值均运行20次,取平均数作为最后的实验结果。表 1~2列出了各算法在两个数据集上的聚类准确率;表 3~4列出了聚类的归一化互信息值。
| 表 1 不同算法在Yale-32数据集上聚类的准确率 Table 1 Clustering accuracy on dataset Yale-32 of different algorithms |
| 表 2 不同算法在COIL20数据集上聚类的准确率 Table 2 Clustering accuracy on dataset COIL20 of different algorithms |
| 表 3 不同算法在Yale-32数据集上归一化互信息 Table 3 NMI on dataset Yale-32 of different algorithms |
| 表 4 不同算法在COIL20数据集上归一化互信息 Table 4 NMI on dataset COIL20 of different algorithms |
由表 1~2可知,在两个数据集上,MCNMFFF算法的聚类准确率平均值相对于其他对比算法的聚类准确率平均值均有了较大的改善。在Yale-32数据集上,MCNMFFF算法比NMF算法的聚类准确率平均提高了9.69个百分点,比GNMF算法平均提高了4.97个百分点,比CNMFS算法平均提高了3.24个百分点,比GCNMFS算法平均提高了1.68个百分点。在COIL20数据集上,MCNMFFF算法比NMF算法的聚类准确率平均提高了8.6个百分点,比GNMF算法平均提高了4.81个百分点,比CNMFS算法平均提高了4.32个百分点,比GCNMFS算法平均提高了2.51个百分点。
同样,由表 3~4可看出,在两个数据集上,MCNMFFF算法、GCNMFS算法、CNMFS算法和GNMF算法的归一化互信息平均值均比NMF算法平均值高得多。在Yale-32数据集上,MCNMFFF算法比NMF算法的聚类准确率平均提高了15.76个百分点,比GNMF算法平均提高了9.72个百分点,比CNMFS算法平均提高了5.81个百分点,比GCNMFS算法平均提高了2.56个百分点。在COIL20数据集上,MCNMFFF算法比NMF算法的聚类准确率平均提高了14.6个百分点,比GNMF算法平均提高了10.22个百分点,比CNMFS算法平均提高了6.34个百分点,比GCNMFS算法平均提高了3.6个百分点。
为了能够更加直观地展示MCNMFFF算法的聚类效果,根据实验数据分别给出了聚类准确率和归一化互信息的对比曲线,如图 2~3所示。从中不难看出:1) MCNMFFF算法要比其他对比算法的聚类准确率和归一化互信息值要高得多,尽管有时候会因外部等因素使结果有一定的波动;2) 由于MCNMFFF算法中结合了特征融合的思想,所以相对于GCNMFS等算法在聚类结果上有一定的提升,从而进一步说明特征融合技术可以进一步提升学习质量;3) NMF和GNMF属于无监督方法,CNMFS、GCNMFS和MCNMFFF属于半监督方法,这三种方法的聚类准确率和归一化互信息值较其他两种方法更高,说明监督方法要比无监督方法的聚类性能更好;4) 由于CNMFS、GCNMFS和MCNMFFF三种方法均添加了稀疏约束,使得三种算法能够得到更好的基于部分的表示,从而得到了比NMF和GNMF算法更好的聚类效果。
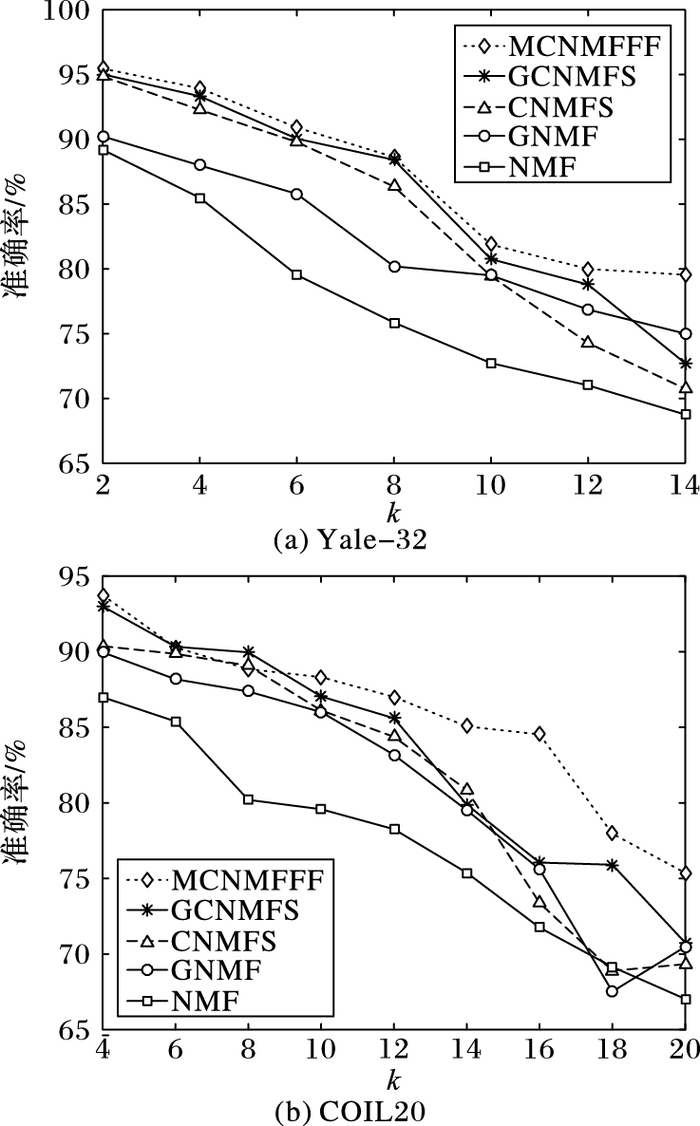
|
图 2 各算法在两个数据集上的聚类准确率曲线 Figure 2 Clustering accuracy curves on two datasets of different algorithms |
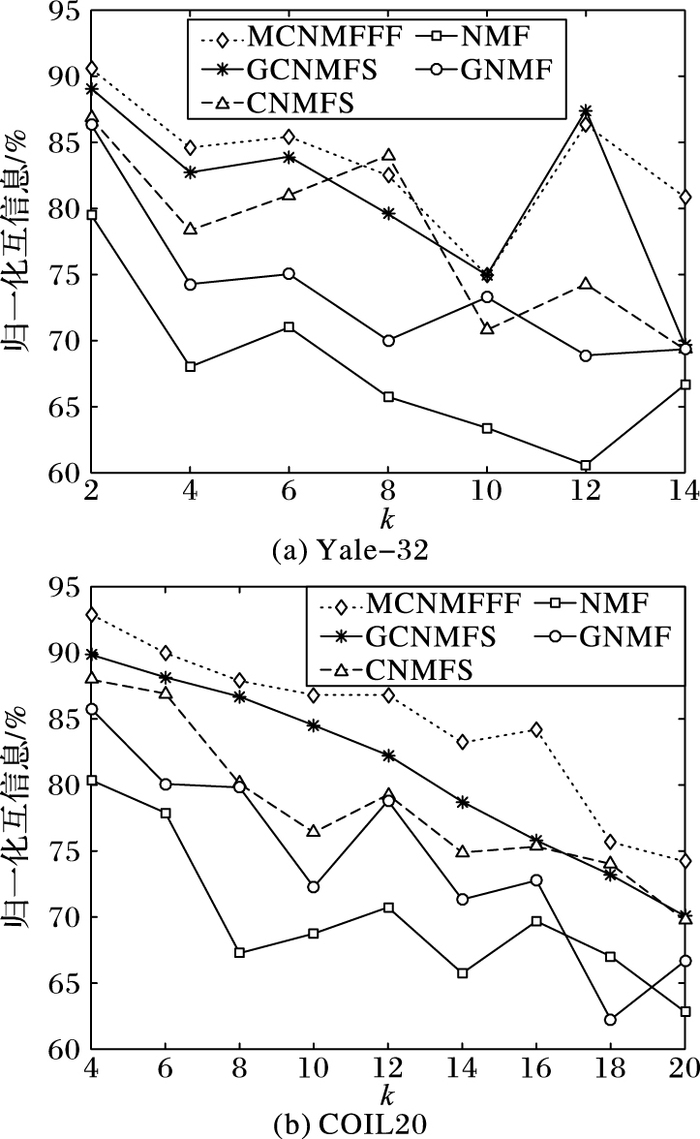
|
图 3 各算法在两个数据集上的归一化互信息曲线 Figure 3 NMI curves on two datasets of different algorithms |
根据MCNMFFF算法的迭代更新式(11)、(14)、(17) 和(20) 可以计算出每一次迭代更新的计算复杂度。考虑到在实际应用中m和n会远远大于k, 因此,迭代更新式(11)、(14) 的主要计算复杂度大约为O(mnk);经过类似的分析,迭代更新式(17)、(20) 的主要计算复杂度大约也为O(mnk)。由于MCNMFFF算法引入了融合系数θ, 完成一次所有向量的更新计算复杂度大约为O(mnk), 而乘性算法完成一次迭代的计算复杂度大约也为O(mnk)。可见,本文提出的MCNMFFF算法在每次更新中,具有与现有算法类似的计算复杂度O(mnk)。
表 5为本文提出的MCNMFFF算法以及其他四种对比算法对每个k值均运行20次,取平均数作为最后的平均运行时间的数据对比。
| 表 5 各算法在两个数据集上的平均运行时间 s Table 5 Mean time on two datasets of different algorithms s |
由表 5可知,从时间复杂度上来分析,改进NMF算法的时间主要用在矩阵分解的迭加上,其他步骤的时间复杂度不会超过NMF算法的时间复杂度。因为各种约束的引入,使得本文提出的MCNMFFF算法的运行时间要明显少于NMF、GNMF和CNMFS算法的运行时间; 但由于MCNMFFF是将GNMF和CNMFS模型分解后的具有不同稀疏度的图像特征进行融合,导致其运行时间略长于GCNMFS算法。因为各种约束以及信息融合技术的引入使得MCNMFFF算法在提高部件学习能力的同时还解决了单一种类特征不能够很好地描述图像语义内容的问题,所以其聚类准确率和归一化互信息依然是几种算法中最高的。因此,综合考虑,本文提出的MCNMFFF算法取得了较好的聚类效果。
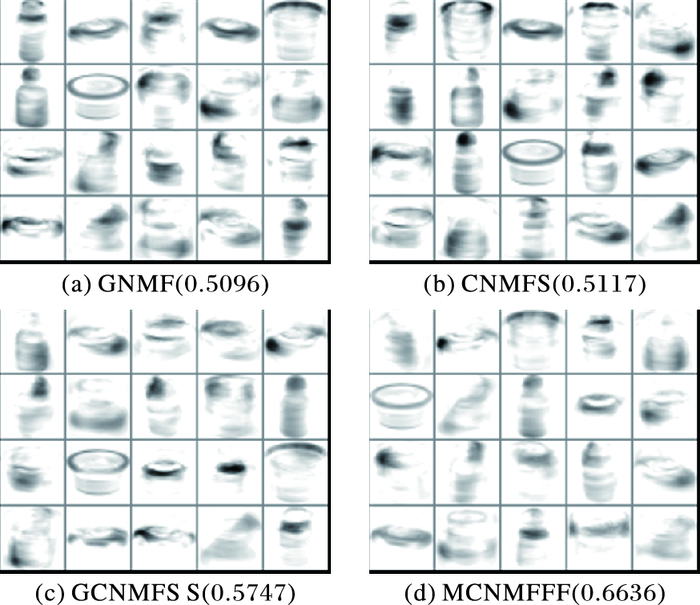
3.4 稀疏度度量在本节实验中,Yale-32和COIL20数据集的特征维数分别取36和20。在两个数据集上分别利用GNMF、CNMFS、GCNMFS和MCNMFFF对原始非负矩阵X进行矩阵分解可以得到基图像,用文献[18]中的稀疏度度量函数来计算其稀疏度。两个数据集的部分基图像示例如图 4~5所示。

|
图 4 不同算法在Yale-32数据集的基图像 Figure 4 Base image of dataset Yale-32 for different algorithms |
|
图 5 不同算法在COIL20数据集的基图像 Figure 5 Base image of dataset COIL20 for different algorithms |
通过在Yale-32和COIL20这两个数据集上对比几种算法基图像的稀疏度可以看出,GNMF算法的稀疏度较差,CNMFS算法的稀疏度一般,而GCNMFS算法的稀疏度略好,MCNMFFF算法的稀疏度最好。由此,表明MCNMFFF算法能够得到图像的最佳局部表示。
4 结语本文提出了基于特征融合的多约束非负矩阵分解算法,并给出了相应的迭代更新规则和收敛性证明。在Yale-32和COIL20两个数据集上对本文算法进行了聚类实验,用聚类准确率和归一化互信息两个评价指标来衡量该算法的聚类性能。从实验结果可以看出,MCNMFFF算法明显优于其他几种对比算法,足以说明MCNMFFF算法的有效性。最后,考察了MCNMFFF算法的稀疏性,结果显示该算法的稀疏度值最高。因此可以得出结论:相对于NMF、GNMF、CNMFS和GCNMFS四种对比算法,MCNMFFF算法能够更好地得到图像的局部表示,使基图像的判别能力更强。但本文算法中的融合系数θ需要通过不断地搜索得到最优值,因此如何有效地选择融合系数θ是以后研究的重点之一。
| [1] | 甘俊英, 何国辉, 何思斌. 核零空间线性鉴别分析及其在人脸识别中的应用[J]. 计算机学报, 2014, 37(11): 2374-2379. (GAN J Y, HE G H, HE S B. Kernel null space linear discriminant analysis and its applications in face recognition[J]. Chinese Journal of Computers, 2014, 37(11): 2374-2379.) |
| [2] | 史卫亚, 郭跃飞, 薛向阳. 一种解决大规模数据集问题的核主成分分析算法[J]. 软件学报, 2009, 20(8): 2153-2159. (SHI W Y, GUO Y F, XUE X Y. Efficient kernel principal component analysis algorithm for large-scale data set[J]. Journal of Software, 2009, 20(8): 2153-2159.) |
| [3] | 尹洪涛, 付平, 沙学军. 基于DCT和线性判别分析的人脸识别[J]. 电子学报, 2009, 37(10): 2211-2214. (YIN H T, FU P, SHA X J. Face recognition based on DCT and LDA[J]. Acta Electronica Sinica, 2009, 37(10): 2211-2214. DOI:10.3321/j.issn:0372-2112.2009.10.018) |
| [4] | KOIDOVSKY Z, TICHAVSKY P, OJA E. Efficient variant of algorithm FastICA for independent component analysis attaining the Cramér-Rao lower bound[J]. IEEE Transactions on Neural Networks, 2006, 17(5): 1265-1277. DOI:10.1109/TNN.2006.875991 |
| [5] | WEI J-J, CHANG C-J, CHOU N-K, et al. ECG data compression using truncated singular value decomposition[J]. IEEE Transactions on Information Technology in Biomedicine, 2001, 5(4): 290-299. DOI:10.1109/4233.966104 |
| [6] | PAATERO P, TAPPER U. Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values[J]. Environmetrices, 1994, 5(2): 111-126. DOI:10.1002/(ISSN)1099-095X |
| [7] | CAI D, HE X, HAN J, et al. Graph regularized non-negative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1548-1560. DOI:10.1109/TPAMI.2010.231 |
| [8] | 李乐, 章毓晋. 非负矩阵分解算法综述[J]. 电子学报, 2008, 36(4): 737-743. (LI L, ZHANG Y J. A survey on algorithms of nonnegative matrix factorization[J]. Acta Electronica Sinica, 2008, 36(4): 737-743.) |
| [9] | LIU H, WU Z, LI X, et al. Constrained non-negative matrix factorization for image representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1299-1311. DOI:10.1109/TPAMI.2011.217 |
| [10] | 胡学考, 孙福明, 李豪杰. 基于稀疏约束的半监督非负矩阵分解算法[J]. 计算机科学, 2015, 42(7): 280-2284. (HU X K, SUN F M, LI H J. Constrained non-negative matrix factorization with sparseness[J]. Computer Science, 2015, 42(7): 280-2284. DOI:10.11896/j.issn.1002-137X.2015.07.060) |
| [11] | 姜小燕, 孙福明, 李豪杰. 基于图正则化和稀疏约束的半监督非负矩阵分解[J]. 计算机科学, 2016, 43(7): 77-82, 105. (JIANG X Y, SUN F M, LI H J. Semi-Supervised non-negative matrix factorization based on graph regularization and sparseness constraints[J]. Computer Science, 2016, 43(7): 77-82, 105. DOI:10.11896/j.issn.1002-137X.2016.07.013) |
| [12] | 李振华, 郑琳川. 全局和局部特征相融合的人脸识别算法[J]. 计算机工程与应用, 2015, 51(14): 131-135. (LI Z H, ZHENG L C. Image recognition algorithm based on global and local features exaction[J]. Computer Engineering and Applications, 2015, 51(14): 131-135. DOI:10.3778/j.issn.1002-8331.1407-0492) |
| [13] | 梅蓉. 基于特征融合的人脸图像识别方法研究[J]. 河南科技学院学报(自然科学版), 2014(4): 70-74. (MEI R. Study of face recognition method based on feature fusion[J]. Journal of Henan Institute of Science and Technology (Natural Sciences Edition), 2014(4): 70-74.) |
| [14] | 兰佩, 方超. 基于全局与局部特征融合的人脸识别方法[J]. 计算机与现代化, 2014(3): 109-113. (LAN P, FANG C. Face recognition method based on global and local features fusion[J]. Computer and Modernization, 2014(3): 109-113.) |
| [15] | RODRIGUEZ J D, PEREZ A, LOZANO J A. Sensitivity analysis of k-fold cross validation in prediction error estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(3): 569-575. DOI:10.1109/TPAMI.2009.187 |
| [16] | DING C, LI T, PENG W, et al. Orthogonal nonnegative matrix tri-factorizations for clustering [C]//KDD 2006: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2006: 126-135. https://link.springer.com/article/10.1007/s10115-008-0134-6 |
| [17] | CHENG Q, LI S Z, ZHANG H, et al. Learning spatially localized, parts-based representation [C]//CVPR 2001: Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2001: 207-212. http://www.sciencedirect.com/science/article/pii/B9780124071711000198 |
| [18] | BERRY M W, PULATOVA S A, STEWART G W. Algorithm 844: computing sparse reduced-rank approximations to sparse matrices[J]. ACM Transactions on Mathematical Software, 2004, 31(2): 252-269. |




