大数据不仅是指数据样本量的庞大, 也意味着数据特征维度的丰富。大数据给人们生活质量带来的飞速提高不亚于其在数据处理上产生的挑战。在人工智能和数据处理领域中, 将包含多维特征向量的高维度的数据降低至易于计算且保留目标特征的低维度数据一直是一个核心议题。所谓数据降维是指通过线性或非线性映射方法将样本从高维空间映射到低维空间, 从而获得高维数据的一个有意义的低维表示的过程[1]。寻找一个即适用于大数据又具有优良鲁棒性的降维算法是解决维数灾难和高维度信息赘余的有效战略[2-3]。
数据降维算法根据对应数据类型的差异一般分为线性降维和非线性降维。线性降维是寻找高维数据在低维空间的线性投影的降维方法, 如广泛使用的主成分分析(Principal Component Analysis, PCA)[4]、线性判别分析(Linear Discriminant Analysis, LDA)[5]等;但此类方法无法准确高效地处理存在于流形曲面的非线性的数据。针对非线性结构的数据, 产生了很多寻找非线性投射模型的非线性降维算法, 如拉普拉斯特征映射(Laplacian Eigenmaps, LE)[6]、随机邻域嵌入(Stochastic Neighbor Embedding, SNE)[7]、t分布随机邻域嵌入(t-Stochastic Neighbor Embedding, t-SNE)[8]等。不同的算法在定义映射模型上有所差异。其中, 建立可以表示数据内部隐藏的关联结构的概率分布模型是数据降维和可视化的常用策略之一。在随机邻域嵌入(Stochastic Neighbor Embedding, SNE)算法中, 利用高维输入数据间的相似关系构建的概率分布模型有效地将高维数据投影到了低维空间中。然而, 这种局部特征算法存在严重的拥挤问题,即高维空间中的数据在投影至低维时, 本来不相似的不同类别会重叠拥挤在低维空间的相同位置上。为了解决拥挤问题, t分布随机邻域嵌入(t-Stochastic Neighbor Embedding, t-SNE)算法在建立概率分布模型中使用到了长尾的t分布模型。在处理人工生成的一般规模的样本时, 这种概率分布模型可以在有效地进行数据降维同时呈现高质量且鲁棒的数据可视化结果。但在面对现实世界中的高数量级别数据时, t-SNE算法的处理结果却不尽如人愿。t-SNE算法在构建原始高维数据的分布模型时只保留了邻近数据的相似度特征, 使得其在不同类型的数据库下的处理结果波动很大。在机器学习领域里, 对于高数量级别数据的数据降维和可视化实现仍是一个挑战。
以t-SNE算法为代表的概率分布模型降维算法在构建高维数据模型时都是参考单一的数据特征, 如相似度、纹理特征、结构特征等, 并且将其作为决定性特征。这种独断的建模使得后续的数据处理可视化不理想且容易受不同数据库影响。因此, 不仅限于一种特征的多种特征交叉建模机制是一种更准确有效的数据处理模型。
为保证保留原始数据的多种有效特征结构, 本文提出一种基于Wasserstein距离的数据降维算法。Wasserstein距离[9], 也称为陆地移动距离, 最早作为衡量直方图差异的测量方式在计算机视觉领域被引入,其定义为解决最小运输问题中将一个概率分布搬运到另一个分布所需要的最小消耗。此消耗由运输过程中所产生的“地面距离”部分和“所占比”部分同时决定。这样的定义使得Wasserstein距离能够更完整地保存数据的多种有效特征结构。Wasserstein距离也应用于机器学习和信号处理的其他方面。Chazel等[10]提出将欧氏距离替换为Wasserstein距离的图形处理算法。同时, Solomon等[11]提出将Wasserstein距离引入三维网格模型的显著度计算中。到目前为止, Wasserstein距离还没有被应用于数据降维和可视化领域。
本文将Wasserstein距离引入降维, 提出了一种基于Wasserstein距离嵌入式模型的降维算法W-map(Wasserstein Embedding method)。该方法利用Wasserstein距离对高维数据建立同时保留相似度和数据结构特征的概率分布模型, 接着在低维空间随机建立一个表示, 在保证高维和低维数据具有相同Wasserstein距离性质的原则下, 构建最优化的低维投射。
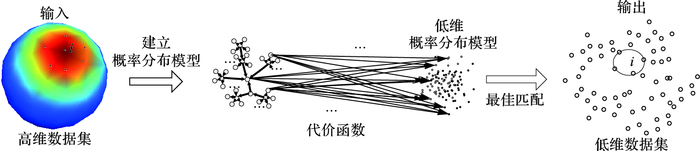
1 W-mapW-map将降维问题转化成最小运输问题, 在高维空间构建了原始数据的Wasserstein距离模型, 用以寻找低维空间中有着相同Wasserstein距离模型的数据, 引入代价函数来引导最匹配的低维数据。流程如图 1所示。
|
图 1 W-map算法流程 Figure 1 Flow chart of W-map |
Wasserstein距离分为两个部分:“地面距离”部分和“所占比”部分。在运输问题中, 对于两个概率分布的Wasserstein距离定义为:
| $W(P,Q) = \mathop {\min }\limits_{\{ {f_{ij}}\} } \sum\limits_{i,j} {{f_{ij}}{d_{ij}}} $ | (1) |
其中:{fij}即为从i分布到j分布的“所占比”部分, 又称为数据表面的Wasserstein流, 用来展示不同运输平面的消耗; dij是i分布到j分布的“地面距离”, 对于W-map最核心的是建立一个相关低维表示的分布, 使这个分布的与原始分布具有较小的差异性, 最终达到拥有一样的表面Wasserstein流。在高维数据中, 本文假设“所占比”的计算是基于数据分类, 当两个数据点的概率分布属于同一类时, 其传输表面的消耗就最低。根据此理论理解, 本文定义分布模型高维空间中所占比可根据高斯核函数的计算公式如下:
| $\mathit{\boldsymbol{f}}({{x}_{i}},{{x}_{j}})=\exp ({{{\left\| {{x}_{i}}-{{x}_{j}} \right\|}^{2}}}/{{{\sigma }^{2}}}\;)$ | (2) |
其中:xi为原始高维数据集上的第i个数据点; fij为第i个分布和第j个分布被投射至再生核希尔伯特空间(Reproducing Kernel Hilbert Space, RKHS)中的两个点的距离, 当两个分布在投射中处于近邻位置, 即属于同一个类别, fij的值将会非常小。
同理, 低维空间中的所占比的计算公式如下:
| $\mathit{\boldsymbol{F}}({{y}_{i}},{{y}_{j}})=\exp ({{{\left\| {{y}_{i}}-{{y}_{j}} \right\|}^{2}}}/{{{\sigma }^{2}}}\;)$ | (3) |
其中: yi为降维后构造出的低维数据集上的第i个数据点。“地面距离”部分dij可以有效度量两个分布的相似性, 通过测地距离、欧氏距离、KL(Kullback-Leibler)熵等不同的相似度度量公式计算得出。随着分布的性质不同, 计算方法不同。
基于Wasserstein距离的概率分布模型的建立结合了“地面距离”部分和“所占比”部分, 将高维和低维的数据分布以Wasserstein距离模型有效地整合在一个便于分析的系统中。在高维数据空间中, 定义xj是xi的近邻点, 其相关的概率分布可表示为概率分布:
| ${{\mathit{\boldsymbol{p}}}_{ij}}=\frac{\exp (-{{f}_{ij}}\centerdot d({{x}_{i}},{{x}_{j}})/\sigma _{i}^{2})}{\sum\limits_{g\ne l}{\exp (-{{f}_{gl}}\centerdot d({{x}_{g}},{{x}_{l}})/\sigma _{g}^{2})}}$ | (4) |
其中:d(xi, xj)为“地面距离”部分, 是xj和xi之间的相似度度量; g是人工设定的对于近邻点的大概范围限定, 在低维概率分布中也有相似的范围限定参数。低维的概率分布定义为:
| ${{\mathit{\boldsymbol{q}}}_{ij}}=\frac{{{(1+{{F}_{ij}}\centerdot d({{y}_{i}},{{y}_{j}}))}^{-1}}}{\sum\limits_{g\ne l}{{{(1+{{F}_{gl}}\centerdot d({{y}_{g}},{{y}_{l}}))}^{-1}}}}$ | (5) |
其中: yi是原始数据xi在低维分布空间的对应投射。本文参考在t-SNE算法中的t分布函数的模型使用来增加不同分布之间的投射距离, 以避免“拥挤问题”。在对比了欧氏距离的测地距离的效果后, 因为其效果差异并不大, 这里的相似度度量d(xi, xj)选择使用计算量相对小的欧氏距离。
1.2 代价函数在建立好概率分布函数后, 需要一个成本函数来衡量建立的低维分布和高维原始分布之间的差异来引导低维分布的修正。当分布P和分布Q中的数据Wasserstein流相似时, 低维数据空间中的数据集Y可用来体现原始高维数据集X的特征。在W-map中, 使用KL散度(KL divergence)[12]来计算其成本函数如下:
| $C=KL(P||Q)=\sum\limits_{i}{\sum\limits_{j}{{{\mathit{\boldsymbol{p}}}_{ij}}}}\log \tfrac{{{\mathit{\boldsymbol{p}}}_{ij}}}{{{\mathit{\boldsymbol{q}}}_{ij}}}$ | (6) |
在不断缩小分布差异的过程中, 可以寻找到与原始数据分布pij最匹配低维数据分布qij, 从而确定其在低维的投影数据集。
1.3 优化策略在利用随机梯度下降法(Stochastic Gradient Descent, SGD)求得成本函数的最小值的过程中, 面对小样本量数据集W-map可以快速得到结果, 但当数据集样本量增大到一定范围, 计算时间就加长了许多。为了解决这个问题, 引入交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)进行优化。
算法1 W-map算法。
输入 高维数据集X={x1, x2, …, xn}。
输出 低维数据集Y={y1, y2, …, yn}。
1) 建立高维空间数据X={x1, x2, …, xn}的概率分布模型pij(式(4))
2) 初始化低维空间数据Y={y1, y2, …, yn}
3) For t=1 to T do
计算低维空间投射qij(式(5))
计算对应的低维空间的Wasserstein流(式(3))
计算成本函数C(式(6))
利用SGD更新Fij
For n=1 to N do
计算成本函数C(式(6))
利用SGD更新qij
End
End
4) 低维数据可视化Y={y1, y2, …, yn}
2 实验本文是用了三个数据集来检验本文提出的降维方法的可视化结果, 其中的一个数据库是人工生成数据库, 下载于http://homepage.tudelft.nl/19j49/Matlab_Toolbox_for_Dimensionality_Reduction.html, 用来生成Brokenswiss的数据库;另外两个数据集为手写体MNIST数据集[13]以及图片数据集Caltech-101[14]。
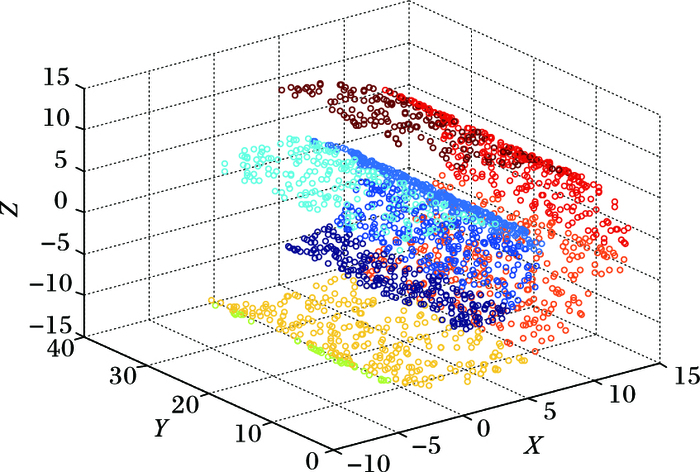
人工生成的Brokenswiss数据集, 用同种颜色标记同类别的数据点, 数据点分布坐标位置如图 2所示。
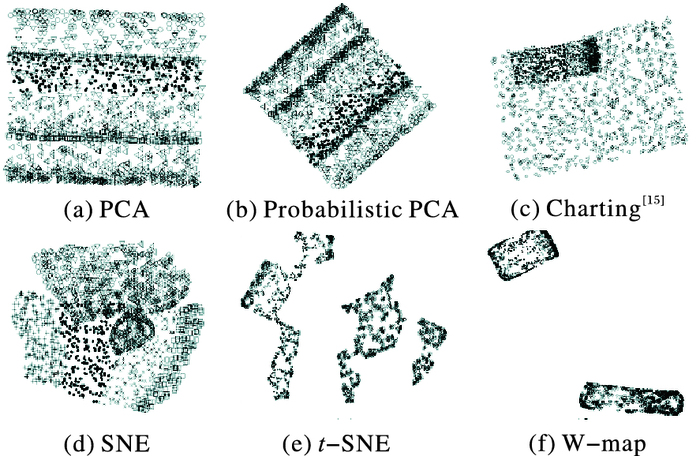
选取另外五种经典概率分布模型降维算法和W-map进行对比, 可视化结果如图 3所示。由图 3可得出, 比起会产生类间叠加和错误分类的PCA、Charting[15]和Probabilistic PCA、SNE、t-SNE和W-map都可以得到较正确的降维可视化结果。SNE的可视化结果相对t-SNE和W-map来说, 同类数据更松散, 类间界限更模糊;但W-map的可视化结果类间界限更清晰, 同时解决了t-SNE产生的同类数据类内断裂问题。这是由于W-map综合了利用Wasserstein距离结合相似度和结构两种特征来进行建模, 使得类内不间断且更可视化效果更紧密, 类间分离清晰。
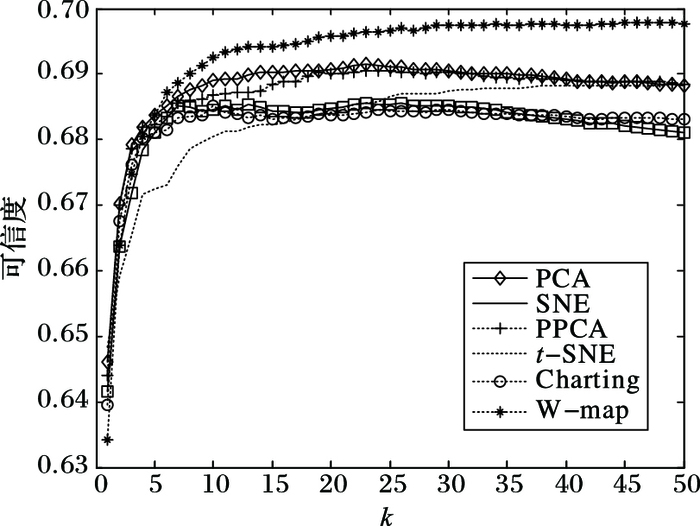
为了更好地分析数据, 对其进行T&C度量分析[16], 所得的信度值如图 4所示。图 4中k为数据点的相邻数据点个数, 与另外五种算法相比,在Brokenswiss数据集中W-map算法拥有更高的可信度, 能够在不改变数据原始结构的前提下更准确地将原始高维数据投射到低维空间中。
|
图 2 Brokenswiss数据集 Figure 2 Original artificial dataset Brokenswiss |
|
图 3 数据集Brokenswiss的降维可视化结果比较 Figure 3 Comparison of dimensionality reduction visualization for dataset Brokenswiss |
|
图 4 Brokenswiss数据集上各算法可信度测量值 Figure 4 Trustworthiness of different example methods on dataset Brokenswiss |
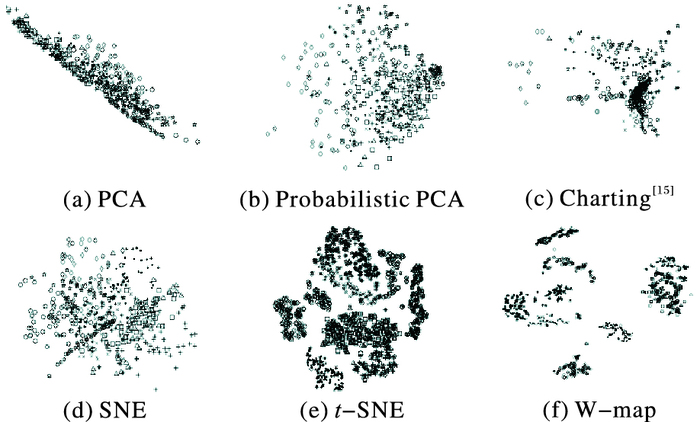
MNIST数据集包含10个类别的60 000张手写数据, 随机选取其中得5 000个样本进行测试, 可视化的结果如图 5所示, 10种类别使用不同的几何图形标价, 包括菱形、正方形、三角形、交叉、黑点等。从图 5中可以看出, 在面对数量级大的显示数据集MNIST时, 相对于PCA、Probabilistic PCA、Charting、SNE,t-SNE和W-map可以产生正确性更高的可视化结果;相对于t-SNE的可视化结果, W-map的类间界限更加清晰。
Caltech101数据集包含102类别的9 000多个样本, 其类别丰富, 包含从动物到飞机到花朵等都包含在内的102种食物图片。随机从中选取15个类别的多个样本进行降维, 同种类别的数据在可视化结果中使用相同颜色标定。从图 6中可以看出, 在复杂多类别的大样本数据集下, SNE和t-SNE在多种数据集中, 鲁棒性较差, 其降维已经无法产生清晰的可视化结果;本文算法W-map在Caltech101数据集中可视化结果显示, 同类别的数据点集合没有因为混杂其他类别数据点的斑点出现, 能够产生正确性高且鲁棒性强的降维结果。
通过五种降维算法在以上三组的数据集的验证, 说明在大多数数据集下, W-map的性能优于现有的降维算法。
|
图 5 数据集手写集MNIST的降维可视化结果对比 Figure 5 Comparison of visualizations for dataset of handwritten digits MNIST |

|
图 6 数据集Caltech101的降维可视化结果对比 Figure 6 Comparison of visualizations for dataset Caltech101 |
本文提出了一种新基于Wasserstein距离的建立概率分布模型的降维方法W-map。不同于其他概率分布模型的降维方法Probabilistic PCA、Charting、SNE和t-SNE, W-map引入Wasserstein距离来保留数据除了局部的结构特征相似度以外的结构信息。通过对PCA、Probabilistic PCA、Charting、SNE、t-SNE和W-map方法的比较, 发现在大部分数据集上概率分布模型的降维方法都可以产生较好的可视化结果, 但对比其他算法, W-map的有效度、信赖性综合较好较稳定。然而, 还需要进一步改进W-map, 使得其能更好地适应更高位更大数量级的现实数据, 同时还可以引入p-Wasserstein距离来进行升级建模。
| [1] | ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323. DOI:10.1126/science.290.5500.2323 |
| [2] | GOTTLIEB L A, KONTOROVICH A, KRAUTHGAMER R. Adaptive metric dimensionality reduction[J]. Theoretical Computer Science, 2016, 620: 105-118. DOI:10.1016/j.tcs.2015.10.040 |
| [3] | 田守财, 孙喜利, 路永钢. 基于最近邻的随机非线性降维[J]. 计算机应用, 2016, 36(2): 377-381. (TIAN S C, SUN X L, LU Y G. Stochastic nonlinear dimensionality reduction based on nearest neighbors[J]. Journal of Computer Applications, 2016, 36(2): 377-381. DOI:10.11772/j.issn.1001-9081.2016.02.0377) |
| [4] | MIKA S, SCHÖLKOPF B, SMOLA A, et al. Kernel PCA and de-noising in feature spaces[EB/OL]. [2017-01-10]. https://alex.smola.org/papers/1999/MikSchSmoMuletal99.pdf. |
| [5] | HASTIE T, TIBSHIRANI R. Discriminant analysis by Gaussian mixtures[J]. Journal of the Royal Statistical Society, 1996, 58(1): 155-176. |
| [6] | BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396. DOI:10.1162/089976603321780317 |
| [7] | HINTON G, ROWEIS S. Stochastic neighbor embedding[J]. Advances in Neural Information Processing Systems, 2002, 41(4): 833-840. |
| [8] | VAN der MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(2605): 2579-2605. |
| [9] | LIPMAN Y, PUENTE J, DAUBECHIES I. Conformal Wasserstein distance: Ⅱ. computational aspects and extensions[J]. Mathematics of Computation, 2011, 82(281): 331-381. |
| [10] | CHAZAL F, COHEN-STEINER D, MÉRIGOT Q. Geometric inference for probability measures[J]. Foundations of Computational Mathematics, 2011, 11(6): 733-751. DOI:10.1007/s10208-011-9098-0 |
| [11] | SOLOMON J, DE GOES F, PEYRÉ G, et al. Convolutional Wasserstein distances: efficient optimal transportation on geometric domains[J]. ACM Transactions on Graphics, 2015, 34(4): 513-526. |
| [12] | VAN ERVEN T, HARREMOS P. Rényi divergence and Kullback-Leibler divergence[J]. IEEE Transactions on Information Theory, 2012, 60(7): 3797-3820. |
| [13] | DE GOES F, COHEN-STEINER D, PIERRE A, et al. An optimal transport approach to robust reconstruction and simplification of 2D shapes[J]. Computer Graphics Forum, 2011, 30(5): 1593-1602. DOI:10.1111/cgf.2011.30.issue-5 |
| [14] | AJEESH S S, INDU M S, SHERLY E. Performance analysis of classification algorithms applied to Caltech101 image database[C]//Proceedings of the 2014 International Conference on Issues and Challenges in Intelligent Computing Techniques. Piscataway, NJ: IEEE, 2014: 693-696. |
| [15] | BRAND M. Charting a manifold[EB/OL]. [2017-01-10]. https://papers.nips.cc/paper/2165-charting-a-manifold.pdf. |
| [16] | MOKBEL B, LUEKS W, GISBRECHT A, et al. Visualizing the quality of dimensionality reduction[J]. Neurocomputing, 2013, 112(1): 109-123. |




