2. 北京科技大学 钢铁共性技术协同创新中心, 北京, 100083
2. Collaborative Innovation Center of Steel Technology, University of Science and Technology Beijing, Beijing 100083, China
旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题。随着城市节点数的增加, 该问题不可能使用穷举方式找到最优解, 是著名的NP-Hard问题。计算智能的发展对该问题的求解提供了很多优化算法, 如遗传算法(Genetic Algorithm, GA)[1]、蚁群优化(Ant Colony Optimization, ACO)算法[2]、文化基因算法(Memetic Algorithm, MA)[3]、模拟退火(Simulated Annealing, SA)算法[4]等。
粒子群优化(Particle Swarm Optimization, PSO)算法自提出以来, 在函数优化问题上取得了极其良好的效果。同遗传算法对比, 粒子群优化算法收敛更快, 结果更优, 因此受到众多研究者关注。尽管如此, 在求解离散问题, 如旅行商问题(TSP)上, 粒子群优化算法中的速度概念, 不能直接地应用在问题模型中, 需要对算法进行一定改进才能适合求解。
目前国内外诸多学者研究了如何将该算法与其他算法结合以求解TSP。Mahi等[5]将蚁群算法和粒子群算法结合, 利用信息素信息对粒子间位置进行更新;Chen等[6]提出了模拟退火蚁群系统粒子群算法, 该算法除了用信息素来处理粒子间信息传递, 还用了遗传算法进行种群迭代, 并利用模拟退火算法增强寻优质量;易云飞等[7]利用蚁群算法的信息素为两城市间的距离赋予权重, 并基于伊藤随机过程定义了漂移算子和波动算子, 用以改进粒子群算法中的学习因子。除了和其他算法相结合使用, 一些研究者将标准粒子群算法中概念加以改进, 以适应离散问题求解;Clerc[8]提出了离散PSO(Discrete PSO, DPSO)算法, 将城市序列定义为粒子的位置, 将城市的交换序定义为粒子的速度, 并为粒子间的飞行运动定义了运算规则, 成功解决了TSP中粒子的更新方式;谢旻[9]将粒子群算法和遗传算法结合, 同时引入克隆免疫机制, 从而设计了克隆算子、交叉算子、自适应变异算子和抗体重组算子来解决粒子间的更新。从已有研究来看, 利用交换子与交换序概念的粒子速度与位置定义方式, 或与其他算法相结合的新式定义算子, 在一定程度上提高了算法的求解质量, 但同时也引入了更多的概念或参数, 使算法本身复杂化。本文提出了一种基于汉明距离的改进的随机贪婪PSO(Improved Random Greedy PSO Based on Hamming Distance, IMRGHPSO)算法, 该算法通过引入汉明距离的概念定义了TSP中粒子间位置与速度的更新。同时设计了2-opt和3-opt算子, 引入粒子重生机制, 进一步提高了算法的寻优能力。
1 TSP的其数学模型TSP的数学描述:给定n个城市的坐标点或城市间的距离矩阵, 从某点出发, 遍历所有城市点, 每个城市只经过一次, 最终回到出发城市点, 求如何选择路径使所走过的总路程最短。若对于城市集合V={V1, V2, …, Vn}, 则一条路径可表示为有序序列C=C1C2…Ci…Cn, 其中Ci∈V(i=1, 2, …, n)。令两城市间距离为d(Ci, Ci+1), TSP的目标即为:
| $ {\rm{min}}\;L{\rm{ = }}\sum\limits_{i = 1}^{n-1} {d\left( {{C_i}, {C_{i + 1}}} \right)} + d\left( {{C_n}, {C_1}} \right) $ | (1) |
在粒子群算法中, 首先产生一定规模的粒子作为问题搜索空间的有效解, 然后通过一定次数迭代, 得到优化结果。和鸟群中的小鸟一样, 每一个粒子都具有速度和位置, 迭代过程中, 由每个粒子本身的历史最优解和群体全局历史最优解来改变粒子的飞行速度和下一个位置, 让粒子在解空间中探索和开发, 最终得到问题的最优结果。
用N维向量来表示粒子的位置, 设群体中有m个粒子, 则第i个粒子的位置可表示为Xi=(Xi1, Xi2, …, XiN), 粒子速度为Vi=(Vi1, Vi2, …, ViN), 其中i=1, 2, …, m。每个粒子的历史最优位置记为pi=(pi1, pi2, …, piN)。整个群体的历史最优位置记为pg=(pg1, pg2, …, pgN)。每一次迭代过程, 粒子需要更新状态。其中, 粒子速度和位置更新公式为:
| $ V_i^{t + 1} = wV_i^t + {c_1}{r_1}\left( {{p_i}-X_i^t} \right) + {c_2}{r_2}\left( {{p_g}-X_i^t} \right) $ | (2) |
| $ X_i^{t + 1} = X_i^t + V_i^{t + 1} $ | (3) |
其中:t表示当前迭代次数; Vit和Xit分别表示第t次迭代时粒子的速度与位置; w为惯性权重, 取值在区间[0, 1]内, 通常初始为0.9, 并随着迭代逐步递减; c1与c2称为学习因子, 通常取c1=c2=2;r1与r2为区间[0, 1]内的随机数。
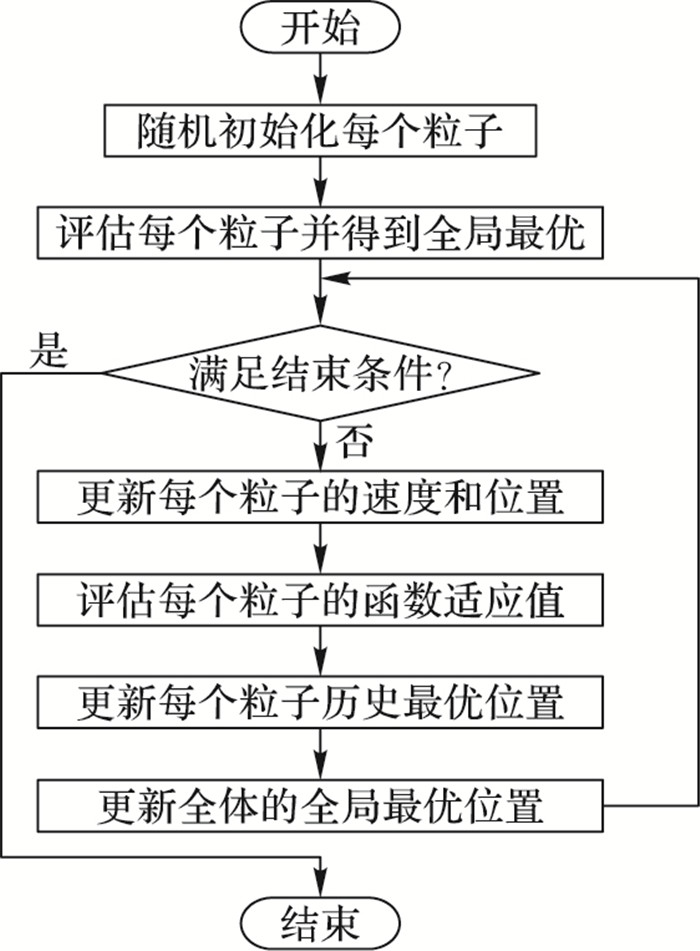
粒子群算法基本流程如图 1所示。
|
图 1 标准PSO流程 Figure 1 Process of standard PSO |
在信息学中, 两个等长的字符串之间, 对应位置上不同的字符的个数即称为汉明距离, 也称为海明距离。换言之, 将一个字符串变换成另一个字符串所需的字符个数即为两个字符串的汉明距离。如两个二进制串:a =[0 1 0 0 0 1], b=[1 0 0 0 1 1], a与b第一、二、五位不同, 即汉明距离为3。
汉明距离已经运用在各类问题上, 如:Rai等[10]将支持向量机和汉明距离相结合运用于虹膜识别系统, 取得了相当高的识别率;Osaba等[11]在利用蝙蝠算法求解TSP时, 引入汉明距离的概念, 改进了该算法中对蝙蝠速度的定义, 在与其他算法的比较后证明改进后的算法求解效果令人满意。
在TSP中, 每一个解是长度为N的一维数组, 不同解之间特征为长度相同, 相对应位置的节点部分不同。以8个城市的TSP为例, 设t时刻有两个可行解:
X1t=[1 3 4 6 2 5 8 7]
X2t=[1 7 4 6 3 5 2 8]
则两个解之间的汉明距离为4。由于TSP的解是一条闭合回路, 因此不相同的两个解有可能代表的是同一个路径, 如路径[1 3 4 6 2 5 8 7]和[4 6 2 5 8 7 1 3], 这两个解所有对应位城市节点编码均不相同, 但是所代表的路径完全相同。因此, 在运用汉明距离概念比较TSP的解时, 需要对解进行一定处理, 将相比较的两个解的起始节点调整为相同节点后, 再进行汉明距离计算。
本文将汉明距离的概念引入粒子群算法当中, 如果将两个解看作两个粒子, 其中一个粒子向另一个粒子飞行需要4个单位汉明距离即可达到, 即汉明距离为4, 记为HMD(X1t, X2t)=4。因此, 在基于汉明距离的粒子群算法中, 定义粒子Xi在第t次迭代中, 受最优粒子Xbest吸引而获得速度为:
| $ V_i^t = {\rm{Random}}\left[{1, HMD\left( {{X_i}, {X_{{\rm{best}}}}} \right)} \right] $ | (4) |
即从1到两者汉明距离之间的随机数, 当该值较大时, 粒子飞行速度较快;反之则较慢。设上述例子中, X1t受X2t吸引, 速度V1t为2, 即随机进行两次位置交换。第一次调整X1t的第二位的节点3变为7, 同时将原有节点中的3变为7, X1t+1=[1 7 4 6 2 5 8 3]。之后, 同理调整第五位, 则X1t+1=[1 7 4 6 3 5 8 2]。这样, 基于汉明距离概念, 该算法成功且简明地设计了粒子与粒子间的距离, 并获得粒子位置更新公式:
| $ X_i^{t + 1} = X_i^t + V_i^t $ | (5) |
速度上限为两粒子间汉明距离, 在此本文算法并未设置其上限为一个更小的数值, 目的是为了使粒子在飞行过程中产生差异化, 从而确保群体的搜索能力。
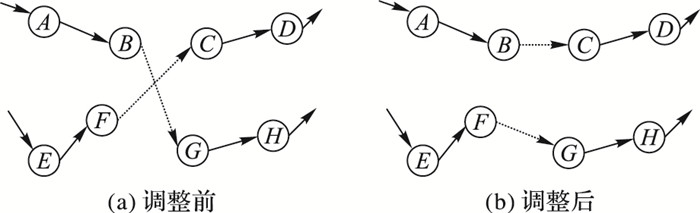
2.3 基于随机贪婪规则的2-opt和3-opt算子在求解TSP的局部路径优化方面, 2-opt[12-14]与3-opt[15-17]是常用的两种优化算子, 通过对TSP路径中边的调整以获得问题一个解的邻域解。在2-opt中, 删除不相邻的两条边, 并重新生成两条边, 如图 2所示。
|
图 2 2-opt算子 Figure 2 2-opt operator |
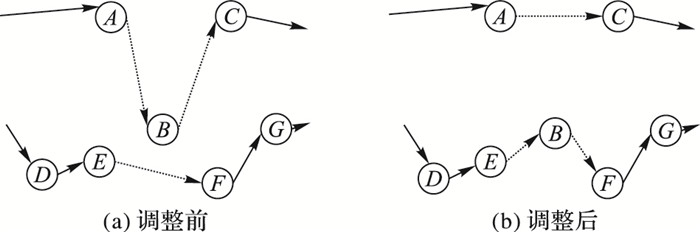
图 2中, 删除d(B, G)和d(F, C), 重新生成d(B, C)和d(F, G), 若d(B, G)+d(F, C)>d(B, C)+d(F, G), 则该2-opt调整后寻得解更优。2-opt的合理运用, 可以大幅缩减一个解的路径总长, 达到更好的寻优。这种局部寻优在算法前期效果极佳, 当结果收敛到一定程度时, 合适的2-opt调整边已经不容易找到, 因此该算子不适用于算法后期,而适合用在初试解的优化和每一次迭代之后, 所有粒子进行邻域的搜寻。相比之下, 在算法后期, 3-opt的调整则更为有效。在路径中连接某点Xi相邻的两条边, 将其删除, 并将Xi-1和Xi+1相连, 在路径中另外两个相邻点Xj和Xj+1之间插入Xi, 此时需重新生成两条边d(Xj-1, Xi)和d(Xi, Xj+1), 实现三条边的调整, 如图 3所示。
|
图 3 3-opt算子 Figure 3 3-opt operator |
图 3中, 删除d(A, B), d(B, C)和d(E, F), 重新生成d(A, C), d(E, B)以及d(B, F), 若能够找到合适的点B, 使得d(A, B)+d(B, C)+d(E, F)>d(A, C)+d(E, B)+d(B, F), 则该3-opt实现了邻域搜索到更优解。在算法前期, 该算子可用来使粒子在自己的邻域内探索需求新的路径; 在算法后期, 可使粒子试图跳出局部最优。
2-opt和3-opt算子的提出, 改善了算法中粒子搜索能力。无论是哪一种算子, 对于随机取点这种方式, 采用后的结果都并不能保证一定会向着更优的方向前进。因此, 需要采用一种规则, 来判断哪些点或者哪些边需要进行操作, 确保粒子的局部搜索向着算法所希望的结果飞行。
对于城市节点Xi, 可以根据TSP的城市数据获得n个城市的距离矩阵dn*n。矩阵中第i行数据代表从城市Xi到其他各城市的距离。通常来讲, 从某点出发到距离该点最近的点, 或较近的点, 通常是一个优质解的路径片段。因此, 可以通过距离矩阵, 使一个解中的城市节点, 尽量去选择较近的其他节点。
贪婪算法, 又称贪心算法(Greedy Algorithm), 常常用在各类优化问题当中[18-19]。它是指在求解一个问题时, 每一步总是作出当前最好的选择。以TSP为例, 由于各城市间距离已知, 则从一个城市出发, 每一次总是选择最近城市。该算法可获得一个可行解, 该解通常不是最优解, 但极有可能是一个较优解, 比随机生成的解优秀很多。在求解大规模TSP局部优化时, 借鉴“贪婪”的思想, 可以使一个粒子中某节点去连接最近几个点中的一个, 称之为随机贪婪规则。运用该规则可以使一个解有很大概率寻求更优的结果, 是跳出局部最优的有效方式[20]。
该规则最有效的使用是在3-opt算子当中。在求解一个TSP中, 设置一个随机贪婪因子g, 如g=3, 即在运用3-opt算则时, 若某城市节点V的下一个邻接节点, 不是距离自身最近的三个城市节点, 则随机选择三个城市中的一个, 插入到V的紧后节点位置。通过大量的实现验证, 在城市数N < 50的情况下, 属于小规模问题, 随机贪婪因子g取2或3;当城市数N>50时, 取[2, 5]内的整数。
2.4 改进粒子搜索能力根据粒子群算法基本原理, 所有粒子会受到最优粒子的吸引, 因此, 该算法在一定时间时会陷入局部最优。若最优粒子无法在短时间内寻得更优的位置, 跳出早熟状态, 其他粒子会逐渐聚拢在局部最优位置。
在2.3节已经为最优粒子设计了局部寻优的方式。当其他粒子接近最优粒子时, 可以停止受最优粒子吸引, 转而和最优粒子一样以2-opt或3-opt方式做局部寻优。但该方式的解搜索空间已经被压缩, 非最优粒子的局部搜索空间依然和最优粒子搜索空间极其接近, 或者已经属于一个局部空间内, 而最优解所在局部很可能与该局部距离较远, 使得陷入局部最优的粒子即使多次进行邻域搜索也无法搜索到最优解所在局部空间。本文算法为最优粒子设计的3-opt搜索已经足够让最优粒子具备较强的局部寻优能力, 因此相比之下, 那些已经接近最优粒子的普通粒子, 其局部搜索已经意义不大。
于是, 将算法进一步改进, 当其他粒子距离最优粒子极为接近时, 将消灭该粒子, 转而重新生成新粒子。新生粒子虽然距离最优解较远, 但是由于群里空间再次被扩大, 且新生粒子与当前最优粒子的汉明距离非常远, 将会获得较不稳定的飞行速度。这种不稳定的速度赋予了粒子群在整体解空间中更强大的搜索能力, 很有可能搜索到之前未到达的局部解邻域, 为群体搜索到新的解奠定了基础。
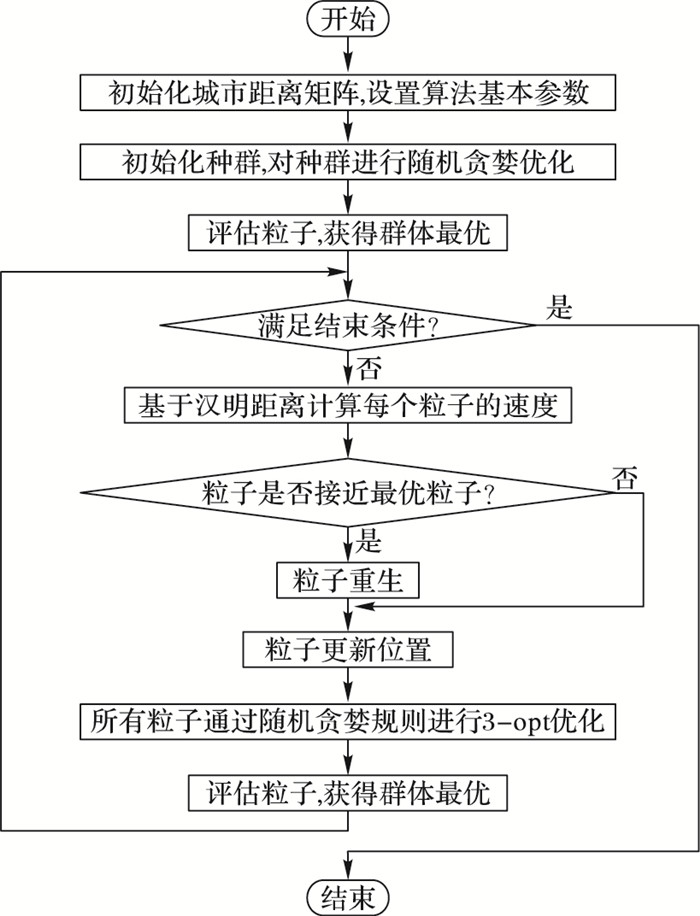
2.5 本文IMRGHPSO算法流程本文提出的IMRGHPSO算法流程如下:
Step1 初试化城市距离矩阵dn*n(n为城市数), 设置基本参数:种群数M; 最大迭代次数T。
Step2 初始化种群, 对种群中的个体以随机贪婪规则进行2-opt优化, 优化次数选取n/10。
Step3 评估粒子, 获得群体最优值。
Step4 计算粒子和最优粒子之间的汉明距离, 并通过式(4) 计算粒子速度。
Step5 根据速度判断粒子是否接近最优粒子, 若接近则消灭粒子并根据Step2中方式重生;否则粒子通过速度更新各自的位置, 最优粒子通过随机贪婪规则进行3-opt优化。
Step6 所有粒子通过随机贪婪规则进行3-opt优化。
Step7 评估粒子, 获得群体最优值。
Step8 判断是否达到结束条件, 若达到则算法结束, 若未达到则返回Step4。
|
图 4 IMRGHPSO算法流程 Figure 4 Process of IMRGHPSO algorithm |
为了验证算法的效果, 选取了标准数据库TSPLIB中一系列数据对本文算法进行验证, 并在处理器为Intel Core i5-5200U 2.20 GHz内存8 GB的计算机上, 使用Matlab进行仿真实验。
各标准算例的测试基本参数如表 1所示。
| 表 1 算法参数 Table 1 Algorithm parameters |
在算例Burma14中, 由于规模较小, 问题较为简单, 并未使用随机贪婪规则, 同样在算例Oliver30中, 也属于较小规模问题, 随机贪婪因子为2, 即在使用随机贪婪规则时, 只考虑最近的两个城市节点。
为了说明算法的效果, 本文对比了基于汉明距离的粒子群算法HPSO, 在HPSO基础上加入贪婪随机规则的RGHPSO, 以及本文提出的IMRGHPSO。表 2为三种算法的结果对比。
| 表 2 HPSO、RGSPSO、IMRGHPSO算法求解TSP结果对比 Table 2 Results comparison of HPSO, RGSPSO and IMRGHPSO for solving TSP |
从表 2可以看出, 在小规模算例中, HPSO已经可以找到最优解, 充分证明基于汉明距离的粒子群算法HPSO是可行的。在中小规模的算例(30 < N < 100) 中, IMRGHPSO算法已经能够获得非常优质的解和最优解的偏离度 < 1%;在大规模城市数TSP算例(N≥100) 中, IMRGHPSO算法在寻找解的质量上有待提高, 偏离度一般能小于5%。在城市数>30的算例结果中可以看出, 随机贪婪规则的引入对于算法性能是有提高的, 随着城市数增加而愈发明显。增加粒子重生的改进算法, 还可以进一步提高算法寻优的能力。
通常来讲, 一种对于算法的改进, 会令算法找到的最优值以及群体平均值都向着更优的方向逼近。而对于优化问题, 以粒子群算法求解TSP为例, 最优的个体才代表该算法的结果, 平均值只是对于群体而言。本文所提出的IMRGHPSO算法在迭代中由于不断有新粒子重生加入, 并未使群体平均值下降, 但正是这一特点, 使得算法可以在解空间寻得更好的结果。
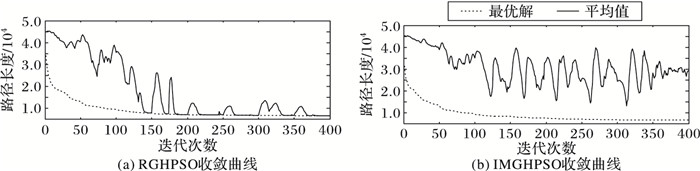
图 5为RGHPSO与IMRGHPSO在求解算例Ch130时的收敛曲线。从图 5可以看出, RGHPSO算法的平均值呈现波动状, 这是由于粒子会进行邻域搜索而导致。IMRGHPSO由于粒子会不断有重生者加入, 其平均值则呈大幅震荡情况, 证明群体在平均值曲线的波峰时差异性很大。从之前给出的结果可以看出, 这种较大的差异性对于该算法的寻优能力具有较大帮助。
|
图 5 Ch130收敛曲线 Figure 5 Convergence curve of Ch130 |
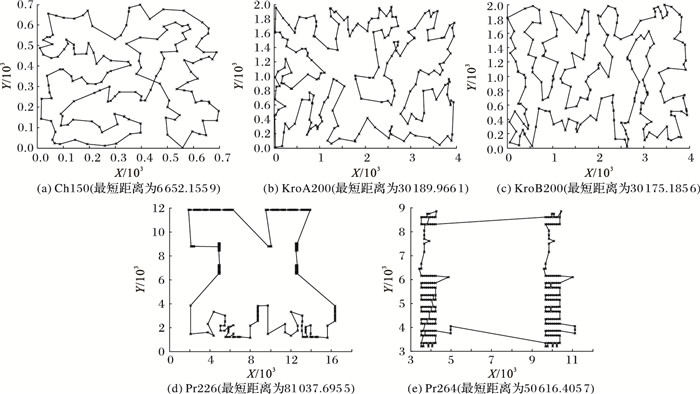
图 6是本文中测试的大规模算例得出的最优路径图。从图 6(a)可以看出, 尽管和已知最优解之间存在偏差, 局部路径可以进一步优化, 但本文算法已经可以求解部分大规模TSP, 其精度有待进一步提高。
|
图 6 最优路径图 Figure 6 Best path graphs |
本文提出了基于汉明距离的改进粒子群算法, 通过定义离散型速度与位置表达式, 使得改进后的粒子群算法更适用于求解TSP。针对算法在后期易陷入早熟的特点, 本文设计了2-opt和3-opt算子用于局部搜索, 并让陷入局部最优的粒子重生以使群体再次获得较大空间搜索新的邻域。通过标准TSP算例的求解, 实验结果表明本文提出的IMRGHPSO算法是有效的。在未来的研究工作中, 该算法在以下方面需进一步提高改进:一是对于TSP问题,本文所提出的汉明距离计算方式存在缺陷,两个解之间相应位置的不同只代表编码的差异,而非两条TSP问题路径的差异, 未来将考虑为TSP汉明距离的计算提出更合理的计算方式;二是算法在求解大规模TSP上精度有待提高, 局部搜索算子需要设计更有效的搜索机制。
| [1] | WANG Y. The hybrid genetic algorithm with two local optimization strategies for traveling salesman problem[J]. Computers & Industrial Engineering, 2014, 70(2): 124-133. |
| [2] | ARIYASINGHA I D I D, FERNANDO T G I. Performance analysis of the multi-objective ant colony optimization algorithms for the traveling salesman problem[J]. Swarm and Evolutionary Computation, 2015, 23: 11-26. DOI:10.1016/j.swevo.2015.02.003 |
| [3] | WANG Y, CHEN Y, LIN Y. Memetic algorithm based on sequential variable neighborhood descent for the minmax multiple traveling salesman problem[J]. Computers & Industrial Engineering, 2016, 106: 105-122. |
| [4] | LIN Y, BIAN Z, LIU X. Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing tabu search algorithm to solve the symmetrical traveling salesman problem[J]. Applied Soft Computing, 2016, 49(C): 937-952. |
| [5] | MAHI M, BAYKAN Ö K, KODAZ H. A new hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem[J]. Applied Soft Computing, 2015, 30(C): 484-490. |
| [6] | CHEN S M, CHIEN C Y. Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques[J]. Expert Systems with Applications, 2011, 38(12): 14439-14450. DOI:10.1016/j.eswa.2011.04.163 |
| [7] | 易云飞, 林晓东, 蔡永乐. 求解旅行商问题的改进粒子群算法[J]. 计算机工程与设计, 2016, 37(8): 2195-2199, 2223. (YI Y F, LIN X D, CAI Y L. Improved particle swarm optimization algorithm for solving traveling salesman problem[J]. Computer Engineering and Design, 2016, 37(8): 2195-2199, 2223.) |
| [8] | CLERC M. Discrete particle swarm optimization, illustrated by the traveling salesman problem [M]//ONWUBOLU P G C, BABU P B V. New Optimization Techniques in Engineering. Berlin: Springer, 2004: 219-239. |
| [9] | 谢旻. 一种混合粒子群优化算法在TSP中的应用[J]. 太原理工大学学报, 2013, 44(4): 506-509, 513. (XIE M. An improved hybrid particle swarm optimization algorithm for TSP[J]. Journal of Taiyuan University of Technology, 2013, 44(4): 506-509, 513.) |
| [10] | RAI H, YADAV A. Iris recognition using combined support vector machine and Hamming distance approach[J]. Expert Systems with Applications, 2014, 41(2): 588-593. DOI:10.1016/j.eswa.2013.07.083 |
| [11] | OSABA E, YANG X S, DIAZ F, et al. An improved discrete bat algorithm for symmetric and asymmetric traveling salesman problems[J]. Engineering Applications of Artificial Intelligence, 2016, 48(C): 59-71. |
| [12] | LOZANO L, SMITH J C, KURZ M E. Solving the traveling salesman problem with interdiction and fortification[J]. Operations Research Letters, 2017, 45(3): 210-216. DOI:10.1016/j.orl.2017.02.007 |
| [13] | WANG Y, CHEN Y, LIN Y. Memetic algorithm based on sequential variable neighborhood descent for the minmax multiple traveling salesman problem[J]. Computers & Industrial Engineering, 2016, 106: 105-122. |
| [14] | 韩伟, 张子成. 求解旅行商问题的离散型贝壳漫步优化算法[J]. 模式识别与人工智能, 2016, 29(7): 650-657. (HAN W, ZHANG Z C. Discrete mussels wandering optimization algorithm for solving traveling salesman problem[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(7): 650-657.) |
| [15] | ZHOU Y, LUO Q, CHEN H, et al. A discrete invasive weed optimization algorithm for solving traveling salesman problem[J]. Neurocomputing, 2015, 151(3): 1227-1236. |
| [16] | 王勇臻, 陈燕, 张金松. 用于求解旅行商问题的多策略离散型和声搜索算法[J]. 华南理工大学学报(自然科学版), 2016, 44(1): 131-138. (WANG Y Z, CHEN Y, ZHANG J S. Multi-strategy discrete harmony search algorithm for solving traveling salesman problem[J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(1): 131-138.) |
| [17] | 程毕芸, 鲁海燕, 黄洋, 等. 求解TSP的自适应优秀系数粒子群优化算法[J]. 计算机应用, 2017, 37(3): 750-754, 781. (CHENG B Y, LU H Y, HUANG Y, et al. Particle swarm optimization algorithm based on self-adaptive excellence coefficients for solving traveling salesman problem[J]. Journal of Computer Applications, 2017, 37(3): 750-754, 781. DOI:10.11772/j.issn.1001-9081.2017.03.750) |
| [18] | 童俊华, 蒋焕煜, 武传宇. 基于贪心算法的温室钵苗稀植移栽路径优化[J]. 农业机械学报, 2016, 47(3): 8-13. (TONG J H, JIANG H Y, WU C Y. Optimization of seedlings lower density transplanting path based on greedy algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 8-13. DOI:10.6041/j.issn.1000-1298.2016.03.002) |
| [19] | 邓晓衡, 曹德娟, 潘琰, 等. 一种基于时延约束的社会网络信用分布优化模型[J]. 计算机研究与发展, 2017, 54(2): 382-393. (DENG X H, CAO D J, PAN Y, et al. An optimized credit distribution model in social networks with time-delay constraint[J]. Journal of Computer Research and Development, 2017, 54(2): 382-393. DOI:10.7544/issn1000-1239.2017.20151118) |
| [20] | MARINAKIS Y, MARINAKI M. A hybrid multi-swarm particle swarm optimization algorithm for the probabilistic traveling salesman problem[J]. Computers & Operations Research, 2010, 37(3): 432-442. |




