2. 上海大学 高性能计算中心, 上海 200444
2. High Performance Computing Center, Shanghai University, Shanghai 200444, China
Navier-Stokes (N-S)方程是流体力学中最重要的方程之一。数学家和物理学家深信,无论是微风还是湍流,都可以通过求解N-S方程来进行解释和预言,因此研究N-S方程具有广泛的应用价值。对N-S方程的研究距今已有200多年的历史,其弱解又称为Leray-Hopf弱解。关于N-S方程强解的局部适定性、存在性与光滑性被列为21世纪7个价值100万美元的数学难题之一。数学家断言,如果没有新的分析工具和数学思想,这个难题将很难得到解决。但是,到目前为止,证明弱解的唯一性和正则性,即强解的整体存在性,仍是一个极具挑战性的问题。只有极少数非常简单的流动问题才能求得其精确解,大多数还是要用离散的方法求得数值解。在利用数值方法对其进行求解时,计算格式的时间步长受制于CFL(Courant-Friedrichs-Lewy)数,CFL=λ·Δτ/Δη,λ是与当地声速成正比的特征函数。当流体近似不可压缩时,λ趋向于无穷大,而CFL数是一个定值,因此最大时间步长Δτ趋向于0。如果用可压缩N-S方程求解近似不可压缩流场,计算效率将会变得极低,因此只能通过不可压缩N-S方程来计算近似不可压流场。不可压缩N-S方程的主要优点是求解未知数的数量较少,将连续性方程和动量方程联立,求解得到速度和压力后,代入能量方程就可以得到温度,计算效率较高。
从原则上讲,不可压缩N-S方程作为描述粘性流体流动的微分方程能够求解流体运动的一切问题。但是不可压缩N-S方程是非线性偏微分方程,在实践中,解决较为复杂的问题,往往要考虑方程的所有项,因此求解非常困难。
现如今,求解不可压缩N-S方程早已不单单是数学家关心的问题,其在工程实际中的应用日益广泛而深入,例如近十年里,对于飞机抖振问题已经逐渐由原来粘、位流分开计算的方法的研究转向基于不可压缩N-S方程的方法的研究[1]。故而在求解过程中,不但计算外形越来越复杂,结构网格类型已经由单一的C型网格、O型网格、H型网格发展到块结构网格、嵌套网格等形式;网格划分的精细程度也随着人们对计算结果可靠性要求的增高而越来越细密。但是,单纯地从细分网格出发去追求计算精度显然是不切实际的,一味地细分网格只会因为计算量过大导致最后计算无法进行。因此,如何从计算方法本身出发,提高计算方法的效率和准确性就成了越来越多的学者关心的问题[2-4]。
有限元法是根据变分原理求解数学物理问题的一种数值方法。自20世纪50年代提出以来,随着矩阵理论、数值分析方法、特别是计算机技术的发展,有限元法无论是在基础理论还是在实现技术上都取得了巨大的进步[5]。它从最初的固体力学领域拓展到传热学、电磁学、流体力学以及声学等其他物理场,从简单的静力分析发展到动态、非线性、多场耦合等复杂计算问题[5]。由于有限元法可以对区域进行任意的划分,更适合用于复杂的计算域,故而在求解微分方程的实际计算中得到越来越多的应用[6]。
传统的有限元方法的通用性最好,但是有限元法在分析波的传播时需要使单元大小与波的波长相当,且时间分辨率也非常小,使得计算效率较低。因此许多学者利用混合有限元法来求解微分方程。由于不可压缩N-S方程具有速度和压力两个变量的性质,利用混合有限元对其进行求解时,离散方程经常不满足inf-sup稳定化条件[7],并且会产生较大的数值震荡。在此基础上,李剑等[8]和何银年等[9]提出了基于局部Gauss积分的稳定化方法。该方法不需要稳定化参数,不需要考虑剖分网格边界的条件,也不需要考虑不同网格单元力的变化;只需要计算两个Gauss积分值之差。这个方法避开了inf-sup条件,稳定了一些低次有限元。许进超[10]提出了用二层或多层网格的方法处理偏微分方程(Partial Differential Equation,PDE)问题。该方法是在粗网格上处理一些离散的非线性问题,得到一个初始值,然后在细网格上求一个离散线性方程组。Girault等[11]提出了一系列求解N-S方程的二层和多层方法。采用两层稳定有限元方法求解N-S方程,可以保持稳定化方法在细网格上的精度,但是多层网格势必会增加计算量,且在粗细网格的交界处处理起来十分困难,如若处理不当,很容易造成二次人为误差。除了有限元法以外,谱方法因其精度高的特点在求解不可压缩N-S方程上也有较为广泛的应用。
谱方法是加权余量法的一种,源于经典的Rize-Galerkin方法,它将未知量用正交函数代替,在整个计算区域内把微分方程离散成代数方程组。这些正交函数往往是一些特殊二阶常微分方程的特征函数,在数学上称之为谱。谱方法最大的魅力在于它具有“无穷阶”收敛性,即如果原方程的解无穷光滑,那么用适当的谱方法所求得的近似解以N-1的任意次速度收敛于精确解,这里的N为所选取的基函数的个数[12]。已有的谱方法一般适用于有界直角区域问题和周期问题,然而,在不可压缩N-S方程的许多实际应用领域中的问题往往都是复杂边界或是无界区域问题和非周期问题。因此,如何将有限元法与谱方法相结合,得到更为通用的高效求解方法是本文较为关注的问题。
谱有限元法是谱方法与有限元方法的结合,它既有谱方法的高精度和收敛快的特点,也有有限元方法可以模拟任何复杂介质模型的特点。谱有限元法中最广为人知的是直接动态刚度矩阵法、确切成员方法和谱元法[13]。谱有限元法和有限元法的主要区别是,有限元法是基于位移多项式的假设,谱有限元法是通过其插值函数来求解波动方程的精确值。与传统有限元法相比,谱有限元法的先进性体现在可以通过单一的分析给出时域和频域两方面的结果[14]。
利用数值方法求解不可压缩N-S方程,随着网格划分数目越多,计算规模会越来越大,当计算规模达到足够大时,计算将会由于机器硬件资源的限制而无法进行。近年来,随着多核处理器的发展,并行计算在一定程度上得以普及,设计合适的并行算法,既可以提高计算速度,又可以缓解内存的不足。谱有限元法和有限元法一样,计算单元之间具有一定的独立性,因此可以采用并行计算,将大规模重复性的单元分析分配在不同的节点上同时进行,将会大大缩短计算的时间,提高计算的效率。
本文的主要工作是通过选取具有无限光滑特性指数函数作为基函数,构造了基于面积坐标的三角网格剖分谱有限元法(Triangular mesh Spectral Finite Element Method based on area coordinate,TSFEM),并用其求解二维定常不可压缩N-S方程,对于方程中的非线性项采用迎风紧致格式计算,能够有效地抑制混淆误差[15]。本文模拟了顶盖驱动的二维方腔流动,分析了实验所得到的结果,并与标准有限元法得到的结果相比较,得出并行TSFEM在求解二维定常不可压缩N-S方程时具有精度高、适用性好和计算效率高的特点。
1 不可压缩N-S方程的谱解法据连续介质力学知识,描述不可压缩粘性流的控制微分方程,包括动量平衡方程、连续方程、本构方程以及能量方程。
为了简单起见,假设x=(x1,x2),流动占据空间Ω={0≤x1,x2≤1}是R2中的有限区域,其边界是Γ=∂Ω,且方程的系数和边界条件均以2π为周期。u(x,t)和p(x,t)分别表示速度向量和压力对密度的比值,0≤t≤n。(x,t),p(x,t)和f(x,t)∈(L2(Ω))2是已知函数不可压缩的N-S方程的齐次Dirichlet边值问题[16]是:
| $\left\{ \begin{matrix} -v{{\nabla }^{2}}u+(u\cdot \nabla )u+\nabla p+f=\frac{\partial u}{\partial t}, & x\in \Omega ,t\in (0,T) \\ divu=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x\in \Omega ,t\in (0,T) \\ u(x,0)=\bar{u}(x)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x\in \Omega \\ \end{matrix} \right.$ | (1) |
方程(1) 中,v是非负常数,称为粘性常数,且有
| $\int_{\Omega }{p(x,0)}dx=0;t\in [0,T]$ | (2) |
设所求的近似解为:
| ${{u}^{N}}(x,t)=\sum\limits_{k=-N}^{N-1}{{{{\hat{u}}}_{k}}{{\Phi }_{k}}(x)}$ | (3) |
其中:Φk(x)为试探函数空间的基函数,k为展开系数。通常取Φk(x)=eikx有共轭Φk(x)且满足:
| $\begin{align} & \int_{0}^{2\pi }{{{\Phi }_{k}}(x){{{\bar{\Phi }}}_{l}}}(x)dx=2\pi {{\delta }_{kl}}= \\ & \left\{ \begin{matrix} 0, & k=l, \\ 2\pi , & k\ne l \\ \end{matrix}k,l=0,1,2,... \right. \\ \end{align}$ | (4) |
其中Φl(x)=e-ilx,l=0,1,2,…,由此可知
对于Fourier谱方法,要求:
| $\int_{0}^{2\pi }{(\frac{\partial N}{\partial t}-L{{u}^{N}}){{{\bar{\Phi }}}_{k}}(x)dx=0,k\in [-N,N-1]}$ | (5) |
其中:L是包含u和u关于空间变量倒数的算子,Lu=-v∇2u+(u·∇)u+∇p+f。将式(3) 代入式(5) 得到:
| $\begin{align} & \sum\limits_{s=-N}^{N-1}{\int\limits_{0}^{2\pi }{{{\Phi }_{s}}(x){{{\bar{\Phi }}}_{k}}(x)dx}\frac{d{{{\hat{u}}}_{k}}}{dt}}-\int\limits_{0}^{2\pi }{L}{{u}^{N}}\cdot {{{\bar{\Phi }}}_{k}}(x)dx=0, \\ & k\in [-N,N-1] \\ \end{align}$ |
由式(4) 得:
| $2\pi \frac{d{{{\hat{u}}}_{k}}}{dt}-\int\limits_{0}^{2\pi }{L{{u}^{N}}\cdot {{{\bar{\Phi }}}_{k}}(x)dx=0,k\in [-N,N-1]}$ |
根据式(1) 得:
| $2\pi \frac{d{{{\hat{u}}}_{k}}}{dt}-(kv{{\hat{u}}_{k}}+ik{{\hat{u}}_{k}}+\nabla p+f)=0$ |
根据给定的初始条件,就可以求出k(t),再代入方程(3) ,就可以得出方程(1) 的近似解uN(x,t)。
2 TFSEM谱有限元法的基本思想是:首先利用有限元的思想将求解区域划分为若干单元,在每个单元内将微分方程进行变分,得到微分方程的积分弱形式;然后将特定参量和未知量在每个单元内用高阶正交多项式(如Chebyshev、Legendre和Fourier多项式等)进行谱近似,得到每个单元的线性方程组,进而得到单元刚度矩阵;利用有限元的技术进行单元的叠加,将单元刚度矩阵组合成总体刚度矩阵;最后得到总求解域的线性代数方程组,加入边界条件,从而求得整个区域的未知变量。有限元法只能通过增加单元来提高精度,谱有限元法不仅可以通过增加单元,还能通过提高每个单元的插值多项式阶数来提高求解精度。此外,采用面积坐标构建三角形单元能够有效地克服谱方法对复杂边界问题实用性不强的弱点。这两方面的改进使得谱有限元法相比其他数值方法具有更大的优势。
2.1 三角形单元谱有限元法平面上有限元的计算单元通常有两种:三角形单元和四边形单元。一般来说,有限元对区域的剖分要求很少,仅仅要求是相容的、正则的或者拟一致的这样一些轻微条件。相对于三角形单元,四边形单元分割起来相对简单,计算精度较高,比较适合较为规则的区域;但是三角形单元适应性更好,求解具有复杂几何构形或具有复杂边界的流动问题时一般不会出现坏单元,若将区域分割成四边形单元很容易出现坏单元,导致计算不收敛。因此对于复杂区域问题多采用三角形单元对其进行划分。
要在三角形单元上使用谱方法,必须建立起三角形区域上的正交多项式。
对于三角形单元,若用直角坐标定义形函数,计算刚度矩阵将十分复杂;而改用面积坐标后,公式可大为简化且积分运算非常简单。故在此本文选择用面积坐标来表示三角形单元[17]。
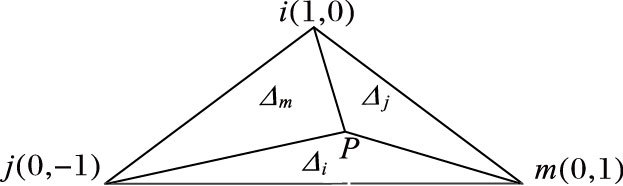
设P为三角形单元中任一点,将P与三角形的三个顶点连接起来形成三个子三角形,如图 1所示。
|
图 1 面积坐标图 Figure 1 Area coordinate system |
P点的坐标p(li,lj,lm)可由三个比值来唯一确定:
li=Δi/Δ
lj=Δj/Δ
lm=Δm/Δ
其中,Δ是△ijm的面积,Δi、Δj、Δm分别是△pjm、△pim、△pij的面积,且有
Δi+Δj+Δm=Δ
假设Ω是R2中的有限区域,f∈(L2(Ω))2,定长的齐次Dirichlet边值问题如下。
求u=(u1,u2)T和p满足:
| $\left\{ \begin{matrix} \text{-}v\Delta u+\sum\limits_{i=1}^{2}{{{u}_{i}}\frac{\partial {{u}_{i}}}{\partial x}+\nabla p=f,} & 在\Omega 内, \\ div\ u=0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & 在\Omega 内, \\ u=0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & 在\partial \Omega 内. \\ \end{matrix} \right.$ | (6) |
其中:v是正常数,称为粘性常数;u称为流体的速度;p是流体的压力; f是流体所受外力。
2.2 混合变分对方程(6) 进行混合变分,定义L2(Ω)的一个封闭子空间为:
| $M=\left\{ q:q\in {{L}^{2}}(\Omega )and\int_{\Omega }{q}dx=0 \right\}$ |
同时,定义另外一个空间
V≡(H01(Ω))2
其中H01(Ω)是Sobolev空间。
记
| $\begin{align} & a(u,v)=v\int_{\Omega }{\nabla u\cdot \nabla vd\Omega } \\ & {{a}_{1}}(w;u,v)=\frac{1}{2}\sum\limits_{i,j=1}^{n}{\int_{\Omega }{{{w}_{j}}(\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}{{v}_{i}}-}}\frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}{{u}_{i}})d\Omega \\ & b(v,q)=-\int_{\Omega }{qdiv\ vd\Omega } \\ & (f,v)\int_{\Omega }{f\cdot vd\Omega } \\ \end{align}$ |
由此可以得到方程(6) 的弱形式:
求u∈V,p∈M,使得
| $\left\{ \begin{matrix} a(u,v)+{{a}_{1}}(w;u,v)+b(v,p)=(f,v), & \forall v\in V, \\ b(u,q)=0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & \forall q\in M \\ \end{matrix} \right.$ |
用谱方法的思想进行方程的离散,选取Chebyshev多项式的极值点作为插值点:
| $\left\{ \begin{align} & {{\xi }_{j}}=-\cos \left( {{\pi }_{j}}/N_{x}^{i} \right) \\ & \ \eta =-\cos \left( {{\pi }_{k}}/N_{y}^{i} \right) \\ \end{align} \right.$ |
选取Φk(x)=eikx,x∈[-1,1],k∈[0,N]作为插值基函数,则u(u1,u2)的插值表达式为:
| $\begin{align} & {{u}^{i}}(\xi ,\eta )=\sum\limits_{j=0}^{N_{x}^{i}}{\sum\limits_{k=0}^{N_{y}^{i}}{u_{jk}^{i}\Phi _{j}^{i}(\xi )}}\Phi _{k}^{i}(\eta ) \\ & {{v}^{i}}(\xi ,\eta )=\sum\limits_{p=0}^{N_{x}^{i}}{\sum\limits_{q=0}^{N_{y}^{i}}{v_{pq}^{i}\Phi _{p}^{i}(\xi )}}\Phi _{q}^{i}(\eta ) \\ \end{align}$ |
根据变分问题
| $a({{u}^{i}},{{v}^{i}})+{{a}_{1}}(w;{{u}^{i}},{{v}^{i}})+b(v,p)=(f,{{v}^{i}})$ |
就可以分别得到各项的表达式,具体求解过程见文献。最后得到原微分方程的离散方程组:
| $\sum\limits_{j=0}^{N_{x}^{i}}{\sum\limits_{k=0}^{N_{y}^{i}}{u_{jk}^{i}(A_{jkpq}^{i}+a\cdot B_{jkpq}^{i})=}}\sum\limits_{j=0}^{N_{x}^{i}}{\sum\limits_{k=0}^{N_{y}^{i}}{f_{jk}^{i}B_{jkpq}^{i}}}$ |
合成刚度矩阵,并求解整个总刚度矩阵的方程组,最终解得各节点上ujki的值。
谱有限元法与有限元法一样要进行问题的划分,将一个规模较大的求解问题划分成多个规模较小的单元求解问题,并且单元内的计算与其他单元之间具有一定的独立性,因此谱有限元法同样适用于做并行计算,这将大大缩短计算所需要的时间,进一步提高计算的效率。
3 数值算例方腔顶盖驱动流(简称方腔流)是一个经典的非定常解问题。几十年来,很多数值方法的研究者都以驱动方腔流动作为模型[18-19]。一方面因其在工业生产中有着广泛的应用;另一方面,求解方腔顶盖驱动流问题可以验证数值方法正确性,从而评价一种数值方法的优劣。
3.1 串行数值实验设计算区域为[0,1]×[0,1],选取Dirichlet边界条件,即在边界上函数值为零。流动雷诺数为:
| $Re={{U}_{up}}L/v$ |
其中Uup为方腔上盖速度,取方腔的边长为特征速度L。
根据前人的数值模拟结果可以得到简单的结论,驱动方腔流动在Re<5000的时候是定常解,在5000<Re<10000左右的时候是非定常周期性解,Re>10000可以得到湍流解。
本文将利用在雷诺数等于100,400,1000,3200,5000,7200,10000时候的标准解来评估本文算法的分辨率和数值精度(如表 1所示)。
| 表 1 不同雷诺数下实验的时间步长与网格数 Table 1 Time-step and grid size of experiment in different Reynolds number |
上边界速度u=1,v=0,压力取Dirichlet边界条件∇p=0;其他三条边界采用无滑移边界条件u=0,v=0,压力取Dirichlet边界条件∇p=0。
计算结束判据为:
| $\begin{align} & \Delta u_{\max }^{n}= \\ & \max [\sqrt{{{(u_{i,j}^{n+1}-u_{i,j}^{n})}^{2}}+{{(v_{i,j}^{n+1}-v_{i,j}^{n})}^{2}}}]<{{10}^{-7}} \\ \end{align}$ |
或者itrTimes<1000,这里的itrTimes指的是迭代次数。
在边界点迎风紧致格式计算过程中考虑到要在边界点上满足不可压缩条件
为了避免四个顶点的压力值出现矛盾边界值,在x=0,y=1点上令p=0,其他三个顶点上则使用线性外插得到的值作为边界值。
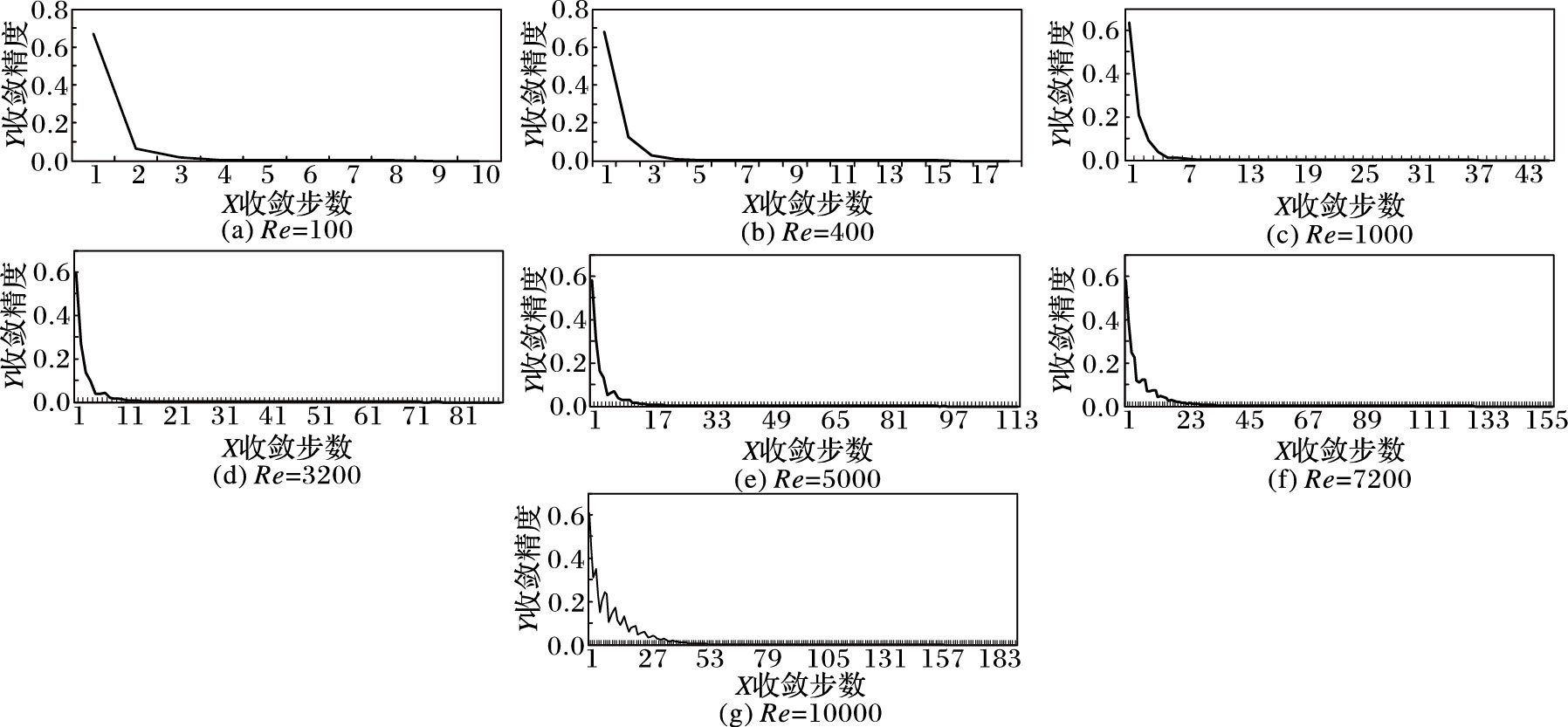
本文计算了和Garoosi等[20]和Ghia等[21]相同雷诺数的驱动方腔流动。图 2和图 3分别给出了雷诺数为100,400,1000,3200,5000,7200和10000情况下的流线图和收敛图。从图 2可以看出本文计算结果与参考文献给出的计算结果相吻合。

|
图 2 不同雷诺数情况下的流线 Figure 2 Streamline in different Reynolds number |
|
图 3 不同雷诺数情况下的收敛 Figure 3 Convergence graph in different Reynolds number |
由图 2中(a)~(b)可以看出,利用TFSEM求解方腔流问题,在低密度网格的划分的条件下,仍然可以获得和高密度划分下传统的有限元方法较为一致的计算结果。这表明谱有限元法解的精度很高;由图 2(c)~(f)和图 3(c)~(f)可以看出在低密度网格划分条件下,TFSEM能够快速收敛。这表明TFSEM在计算二维不可压缩N-S方程时具有谱方法的无穷收敛性。
3.2 并行实验设计与有限元法计算刚度矩阵一样,TSFEM先分别计算各个单元刚度矩阵,然后将单元刚度矩阵集成到整体刚度矩阵。不同单元刚度矩阵计算之间没有直接联系,非常适合针对不同单元刚度矩阵设计并行算法。采用OpenMP将上述算法并行化,对驱动方腔内剪切流动问题进行了计算。OpenMP是一个为在共享存储的多处理机上编写并行程序而设计的应用编程接口,由一个小型的编译器命令集组成,包括一套编译制导语句和一个用来支持它的函数库。
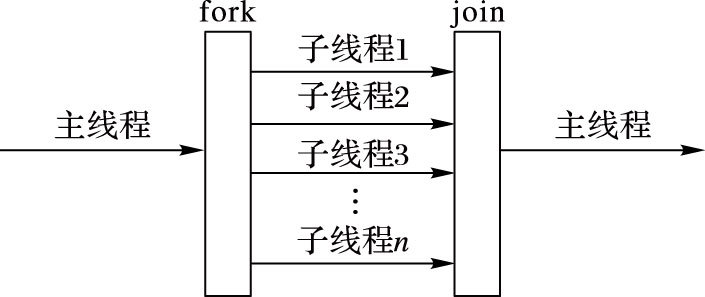
OpenMP采用fork-join并行执行模式,如图 4所示:OpenMP程序首先由主线程执行。需要并行计算时,主线程派生出子线程来执行并行任务。并行代码执行结束,子程序退出或者阻塞,不再工作,控制流程回到单独的主线程中。定义在成对的fork和join之间的区域,称为并行域。
|
图 4 fork-join并行执行模式 Figure 4 fork-join parallel execution model |
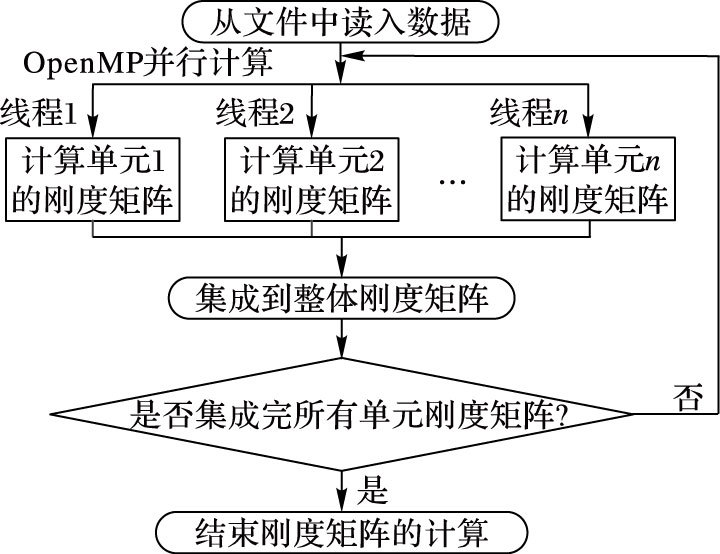
图 5给出了整体刚度矩阵并行计算流程,采用如图 5所示的并行计算流程。实验环境:CPU为4核;每个核分4个线程,共计16个线程,将计算任务平均分配给每个线程。
|
图 5 整体刚度矩阵并行计算流程 Figure 5 Parallel computing process of global stiffness matrix |
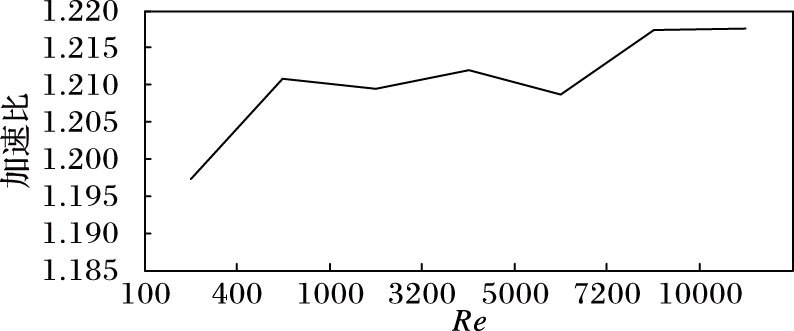
图 6给出了不同了雷诺数下的加速比,通过观察图 6可以清楚地看出,随着雷诺数的增加,加速比在总体上呈现上升的趋势,但是当雷诺数Re>7200时,加速比达到峰值并趋于稳定。如何进一步提高并行算法效率是下一步研究的问题。
|
图 6 不同雷诺数下的加速比 Figure 6 Speed-up ratio in different Reynolds number |
谱有限元法即具有有限元法适应性强的特点又具有谱方法的精度和无穷收敛的特性。本文构造了二维不可压缩N-S方程的并行谱有限元解法,其具体的优点体现在如下几点:
1) 插值精度较高,对于具有波动性的方程,只需要很少的点就可也模拟出原函数。
2) 基函数是无限光滑的指数函数,具有无限可微性,适用于大雷诺数下湍流的计算。
3) 基函数形式简单,与待插函数形式无关。
4) 运用并行计算可以在一定程度上缩短计算时间,提高计算效率。
本文使用谱基函数,推导出求解N-S方程的Galerkin积分表达式并通过并行的方式计算方腔流来进行验算,得到了较好的结果,证实了此格式的适用性。但是当实验网格数进一步增多,进程与进程之间的通信量将会增大,计算时间反而会增加,使得计算效率低下。因此,如何减少并行计算之间的通信,使得计算能够在更大规模的问题上进行,从而提高该算法在并行计算上的通用性将会成为接下来研究的重点。
| [1] | 樊枫, 徐国华, 史勇杰. 基于N-S方程的剪刀式尾桨前飞状态气动力计算研究[J]. 空气动力学学报, 2014, 32 (4) : 527-533. ( FAN F, XU G H, SHI Y J. Computation research on aerodynamic force of scissors tail-rotor in forward flight based on the N-S equations[J]. Acta Aerodynamica Sinica, 2014, 32 (4) : 527-533. ) |
| [2] | REKATSINAS C S, NASTOS C V, THEODOSIOU T C, et al. A time-domain high-order spectral finite element for the simulation of symmetric and anti-symmetric guided waves in laminated composite strips[J]. Wave Motion, 2015, 53 : 1-19. doi: 10.1016/j.wavemoti.2014.11.001 |
| [3] | SAMARATUNGA D, JHA R, GOPALAKRISHNAN S. Wavelet spectral finite element for modeling guided wave propagation and damage detection in stiffened composite panels[J]. Structural Health Monitoring, 2016, 15 (3) : 317-334. doi: 10.1177/1475921716640468 |
| [4] | AXELSSON O, FAROUQ S, NEYTCHEVA M. A preconditioner for optimal control problems, constrained by Stokes equation with a time-harmonic control[J]. Journal of Computational & Applied Mathematics, 2016, 310 : 5-18. |
| [5] | 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003 : 5 -9. ( WANG M C. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003 : 5 -9. ) |
| [6] | RANNACHER R. Finite Element Methods for the Incompressible Navier-Stokes Equations[M]//Fundamental Directions in Mathematical Fluid Mechanics. Berlin:Springer, 2000:191-293. |
| [7] | 杨建宏. 定常Navier-Stokes方程的三种两层稳定有限元算法计算效率分析[J]. 数值计算与计算机应用, 2011, 32 (2) : 117-124. ( YANG J H. Computation efficiency on three kinds of two-level stabilized finite element methods for stationary Navier-Stokes equations[J]. Journal of Numerical Methods and Computer Applications, 2011, 32 (2) : 117-124. ) |
| [8] | 于佳平, 史峰, 李剑, 等. 应用四边形单元稳定化有限元方法求解定常不可压缩流动问题[J]. 工程数学学报, 2012, 29 (2) : 309-316. ( YU J P, SHI F, LI J, et al. Numerical applications of the new stabilized quadrilateral finite element method for stationary incompressible flows[J]. Chinese Journal of Engineering Mathematics, 2012, 29 (2) : 309-316. ) |
| [9] | 黄鹏展, 何银年, 冯新龙. 解Stokes特征值问题的一种两水平稳定化有限元方法[J]. 应用数学和力学, 2012, 33 (5) : 588-597. ( HUANG P Z, HE Y N, FENG X L. A two-level stabilized finite element method for the Stokes eigenvalue problem[J]. Applied Mathematics and Mechanics, 2012, 33 (5) : 588-597. ) |
| [10] | 许进超. 数值格式的稳定性,相容性和收敛性[J]. 中国科学(数学), 2015, 45 (8) : 1205-1216. ( XU J C. On the stability, consistency and convergence of numerical schemes[J]. Science in China(Series A), 2015, 45 (8) : 1205-1216. ) |
| [11] | CHACON REBOLLO T, GIRAULT V, MURAT F, et al. Analysis of a coupled fluid-structure model with applications to hemodynamics[J]. SIAM Journal on Numerical Analysis, 2016, 54 (2) : 994-1019. doi: 10.1137/140991509 |
| [12] | BIRGERSSON F, FERGUSON N S, FINNVEDEN S. Application of the spectral finite element method to turbulent boundary layer induced vibration of plates[J]. Journal of Sound & Vibration, 2003, 259 (4) : 873-891. |
| [13] | GOPALAKRISHNAN S, CHAKRABORTY A, MAHAPATRA D R. Spectral Finite Element Method[M]. London: Springer, 2008 : 177 -217. |
| [14] | 刘宏, 傅德薰, 马延文. 迎风紧致格式与驱动方腔流动问题的直接数值模拟[J]. 中国科学(A辑), 1993, 23 (6) : 657-665. ( LIU H, FU D X, MA Y W. Direct numerical simulation on the problem of upwind compact scheme and driven cavity flow[J]. Science in China (Series A), 1993, 23 (6) : 657-665. ) |
| [15] | 向新民. 谱方法的数值分析[M]. 北京: 科学出版社, 2000 : 48 -90. ( XIANG X M. Numerical Analysis of Spectral Method[M]. Beijing: Science Press, 2000 : 48 -90. ) |
| [16] | 黄冬冬.用Fourier谱方法求解二维椭圆方程Dirichlet边值问题[D].长春:吉林大学,2010. ( HUANG D D. The Fourier spectral method for solving two-dimensional elliptic partial differential equations with Dirichlet boundary condition[D]. Changchun:Jilin University, 2010. ) |
| [17] | 王健平. 有限谱有限元法求解二维不可压缩Navier-Stokes方程[J]. 力学研究, 2014, 3 (3) : 33-42. ( WANG J P. A finite spectral finite element method for incompressible Navier-Stokes equations[J]. International Journal of Mechanics Research, 2014, 3 (3) : 33-42. doi: 10.12677/IJM.2014.33004 ) |
| [18] | GRILLET A M, YANG B, KHOMAMI B, et al. Modeling of viscoelastic lid driven cavity flow using finite element simulations[J]. Journal of Non-Newtonian Fluid Mechanics, 1999, 88 (1/2) : 99-131. |
| [19] | 陈雪江, 秦国良, 徐忠. 谱元法和高阶时间分裂法求解方腔顶盖驱动流[J]. 计算力学学报, 2002, 19 (3) : 281-285. ( CHEN X J, QIN G L, XU Z. Spectral element method and higher-order fractional step method for lid driven flow in closed square cavity[J]. Chinese Journal of Computational Mechanics, 2002, 19 (3) : 281-285. ) |
| [20] | GAROOSI F, BAGHERI G, RASHIDI M M. Two phase simulation of natural convection and mixed convection of the nanofluid in a square cavity[J]. Powder Technology, 2015, 275 : 239-256. doi: 10.1016/j.powtec.2015.02.013 |
| [21] | OSSWALD G A, GHIA K N, GHIA U. Simulation of dynamic stall phenomenon using unsteady Navier-Stokes equations[J]. Computer Physics Communications, 1991, 65 . |




