图像处理技术在现代工业中有着非常广泛的应用,在计算机图像处理技术中,曲线拟合是其基本内容之一,目的是从图像中抽取特征信息进行后续处理。最常用的曲线拟合方法是最小二乘法,其根据目标函数进行相应曲线拟合。点、直线以及二次曲线例如椭圆、圆等是基本的图像特征。现实生活中,大量物体的透视投影由于镜头与被拍摄物体角度的关系均为椭圆,所以椭圆拟合是后续物体辨识与测量的重要条件[1]。但是在实际图形检测中,有大量噪声和用基本图像处理技术难以剔除的孤立点,所以需要找到一种更加有效、易用的椭圆拟合算法。
目前常用的椭圆拟合方法有最小二乘法[2-3]、Hough变换法[4-5]和Kalman滤波法[6]。这些方法中,基于最小二乘的方法适用于各种复杂的对象模型[7]。最小二乘法中根据距离的定义,一般又分为:基于代数距离最小的方法和基于几何距离最小的方法[8]。基于代数距离最小的方法为通过使各离散点到要拟合椭圆的代数距离平方和最小来确定椭圆各个系数。该算法简单、易实现,并且可以得到闭合结果,但是它将所有样本点都当作准确值,当出现噪声时拟合误差较大,识别率下降。基于几何距离最小的方法是将误差距离定义为给定点到几何特征拟合点之间的正交的最短距离。该方法理论上比代数拟合有更好的拟合结果,但是该算法的目标函数表达式复杂,且求解量很大,不易实现,所以最小二乘拟合椭圆中该方法并不常用。莱特准则对椭圆拟合进行优化的前提就是使用最小二乘法的代数距离最小方法拟合一次椭圆,然后针对该方法的缺点与不足进行优化与改进。
本文开发的香烟圆度检测系统,是在无法从端面获取香烟参数的情况下,结构光在烟条纵截面上方一定距离处以固定角度照射在烟条上,形成月牙状光斑。工业相机在光斑垂直正上方进行图像抓取。因为图像中获得的投影光斑仅能得到近似于1/3的弧段,所以最主要的工作是根据该段不完整轮廓进行最优椭圆拟合。但在拍摄过程中,因为烟条的高速运动和外界震动,不可避免地会存在误差较大的样本拟合点。若只用最小二乘法进行拟合,拟合误差较大,不能满足检测要求。因此本文提出一种改进算法:基于莱特准则的椭圆拟合算法,该算法可以剔除误差点,得到更加准确的拟合椭圆,从而可以准确地计算香烟圆度。
1 基于代数距离的最小二乘椭圆拟合基于代数距离最小的最小二乘椭圆拟合方法已经被广泛使用,具体算法步骤本文不再详细介绍,可参考文献[9-11]。平面内有点M(x0,y0),曲线方程f(x,y)=0,则f(x0,y0)指的就是点M到曲线的代数距离。因为最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配,则将样本点距离该曲线的代数距离作为误差,运用最小二乘法得到的椭圆拟合目标函数为:
| $\begin{align} & f(x,y)=(\sum\limits_{i=1}^{N}{(Ax_{i}^{2}+Bxy+Cy_{i}^{2}+D{{x}_{i}}}+E{{y}_{i}}+1){{)}^{2}} \\ & (i=1,2,...,N) \\ \end{align}$ | (1) |
其中:i=1,2,…,N。通过求目标函数的最小值来确定椭圆参数A、B、C、D、E,由极值原理可知,求最小值需要:
| $\begin{align} & \frac{\partial f(x,y)}{\partial A}=\frac{\partial f(x,y)}{\partial B}=\frac{\partial f(x,y)}{\partial C}= \\ & \frac{\partial f(x,y)}{\partial D}=\frac{\partial f(x,y)}{\partial E}=0,(F=1) \\ \end{align}$ | (2) |
由此得到一个方程组:
| $\left[ {\matrix{ {\sum\limits_{i = 1}^N {x_i^4} } & {\sum\limits_{i = 1}^N {x_i^3{y_i}} } & {\sum\limits_{i = 1}^N {x_i^2y_i^2} } & {\sum\limits_{i = 1}^N {x_i^3} } & {\sum\limits_{i = 1}^N {x_i^2{y_i}} } \cr {\sum\limits_{i = 1}^N {x_i^3{y_i}} } & {\sum\limits_{i = 1}^N {x_i^2y_i^2} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^3} } & {\sum\limits_{i = 1}^N {x_i^2{y_i}} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^2} } \cr {\sum\limits_{i = 1}^N {x_i^2y_i^2} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^3} } & {\sum\limits_{i = 1}^N {y_i^4} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^2} } & {\sum\limits_{i = 1}^N {y_i^3} } \cr {\sum\limits_{i = 1}^N {x_i^3} } & {\sum\limits_{i = 1}^N {x_i^2{y_i}} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^2} } & {\sum\limits_{i = 1}^N {x_i^2} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}} } \cr {\sum\limits_{i = 1}^N {x_i^2{y_i}} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}^2} } & {\sum\limits_{i = 1}^N {y_i^3} } & {\sum\limits_{i = 1}^N {{x_i}{y_i}} } & {\sum\limits_{i = 1}^N {y_i^2} } \cr } } \right]\left[ {\matrix{ A \cr B \cr C \cr D \cr E \cr } } \right] + \left[ {\matrix{ {\sum\limits_{i = 1}^N {x_i^2} } \cr {\sum\limits_{i = 1}^N {{x_i}{y_i}} } \cr {\sum\limits_{i = 1}^N {y_i^2} } \cr {\sum\limits_{i = 1}^N {{y_i}} } \cr {\sum\limits_{i = 1}^N {{x_i}} } \cr } } \right] = 0$ | (3) |
通过解线性方程组可得知方程系数(A,B,C,D,E)的值,从而初步确定出椭圆的信息,可以得知椭圆的长轴:
| ${{a}^{2}}=\frac{2(Ax_{0}^{2}+Cy_{0}^{2}+B{{x}_{0}}y{}_{0}-1)}{A+C-\sqrt{{{(A-C)}^{2}}+{{B}^{2}}}}$ | (4) |
短轴:
| ${{b}^{2}}=\frac{2(Ax_{0}^{2}+Cy_{0}^{2}+B{{x}_{0}}y{}_{0}-1)}{A+C+\sqrt{{{(A-C)}^{2}}+{{B}^{2}}}}$ | (5) |
旋转角度:
| $\theta =\frac{1}{2}{{\tan }^{-1}}(\frac{B}{A-C})$ | (6) |
其中x0、y0为该椭圆的中心坐标。
2 莱特准则优化椭圆拟合算法根据高斯误差理论,当测量值服从正态分布时,残差落在三倍方差,即[-3σ,3σ]区间的概率超过99.7%,落在此区间外的概率只有不到0.3%,因此,可以认为残差落于该区域之外的测量值为异常值[12]。这就是莱特准则判别方法,也常称为3σ方法。
2.1 采样点正态分析待拟合曲线为图 1中的虚线曲线,黑色椭圆曲线为最小二乘法拟合的结果。XOY坐标系为像素坐标系。过待拟合曲线上一点p′与椭圆中心o′作连线,连线与椭圆交于点p,则p′p为两点间的代数距离,也是椭圆优化算法的输入值。
因莱特准则具有一个约束条件,要求数据服从正态分布,所以对输入值进行正态分析检验。
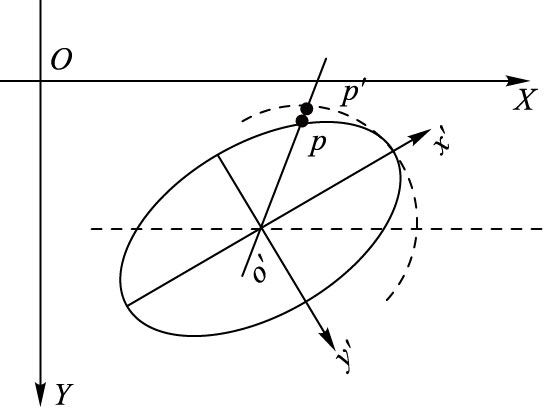
|
图 1 莱特准则数据样本点集 Figure 1 Data sample point set of Letts criterion |
如图 2所示,使用Minitab软件对一组实验数据(单位:mm)进行正态检验,图 2中横坐标表示由图 1中得到的两点间的代数距离,纵坐标表示各值分布的概率密度。P(图 2中的P-Value)值在Minitab中表示假设事件的差异性,在统计学中通常用0.05作为判断标准。P大于0.05表示假设的事件无差异,小于0.05表示有差异。假设该组数据服从正态分布,检验结果显示P=0.422>0.05,表示假设的数据服从正态分布事件无差异。通过多组实验数据验证,由p′p构成的数组服从正态分布,说明可以使用莱特准则进行分析。
2.2 基于莱特准则进行椭圆优化在OpenCV中,椭圆拟合函数cvFitEllipse[13-15]拟合椭圆的原理就是利用最小二乘法。由此函数可得到拟合出的椭圆在像素坐标系下的中心o′(center.x,center.y),椭圆的长轴a,短轴b,以及偏转角θ。以o′为原点的坐标系x′o′y′和图像像素坐标系XOY间的关系如图 1所示。则代数距离最小的最小二乘法拟合的椭圆在XOY坐标系下的方程为:
| $\frac{{{(x'\cos \theta -y'\sin \theta )}^{2}}}{{{a}^{2}}}+\frac{{{(x'\sin \theta +y'\cos \theta )}^{2}}}{{{b}^{2}}}=1$ | (7) |
| $x=x'+center.x$ | (8) |
| $y=y'+center.y$ | (9) |
待拟合曲线上的每点坐标可由OpenCV函数得知,过椭圆中心与待拟合曲线上某点的直线方程为:
| $y=\frac{{{y}_{i}}-center.y}{{{x}_{i}}-center.x}x,(1=1,2,...,N)$ | (10) |
其中p′(xi,yi)为待拟合曲线上某点的坐标。
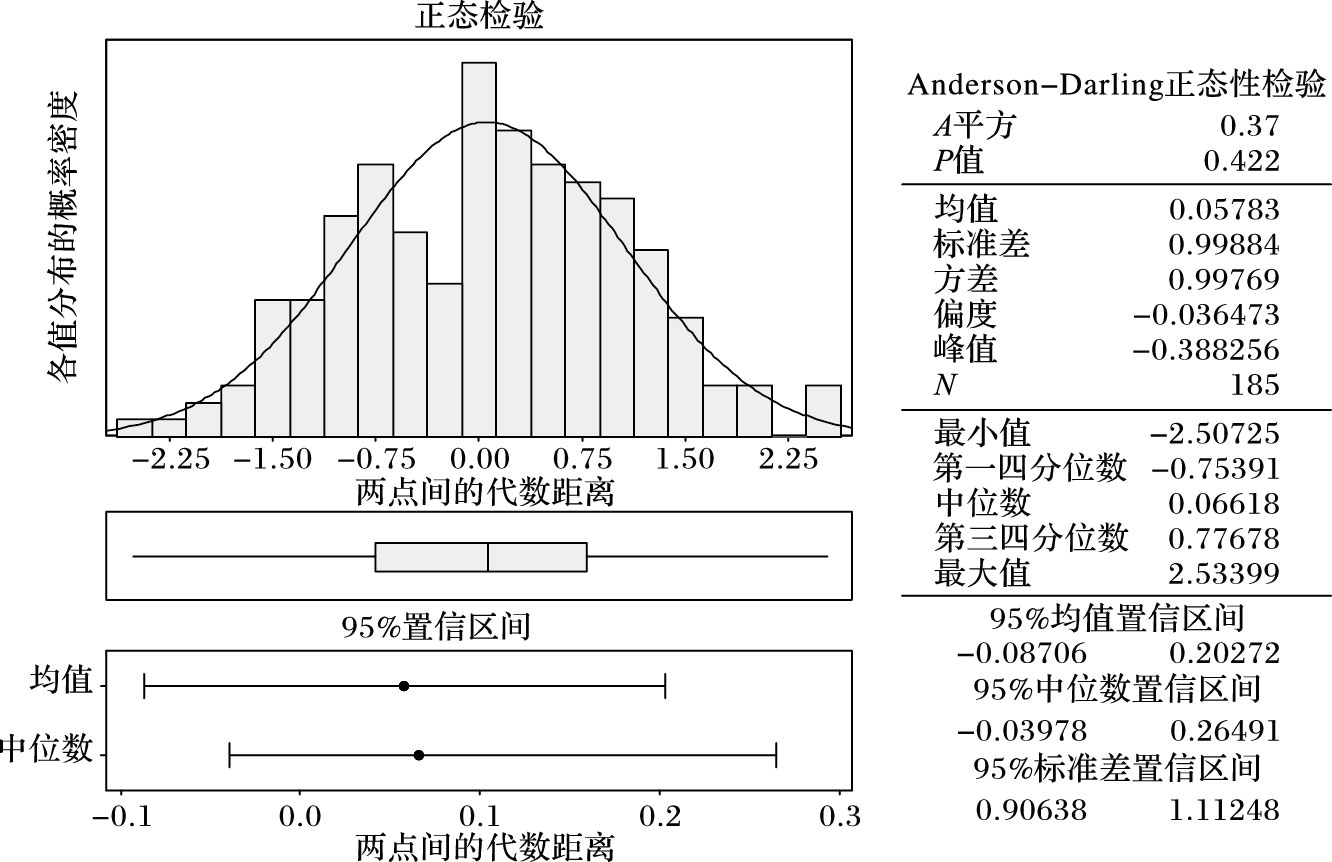
|
图 2 样本点正态分析结果 Figure 2 Normal distribution results of sample points |
联立方程(7) ~(10) ,求出点p′(xi,yi)与其对应的拟合椭圆上的点p(xi,yi)像素坐标,则两点间的代数像素距离为:
| $\begin{align} & l(i)=\sqrt{{{({{x}_{ip'}}-center.x)}^{2}}+{{({{y}_{ip'}}-center.y)}^{2}}}- \\ & \sqrt{{{({{x}_{ip}}-center.x)}^{2}}+{{({{y}_{ip}}-center.y)}^{2}}};(i=1,2,...N) \\ \end{align}$ | (11) |
对样本点集l(i)进行基于莱特准则的数据分析,将l(i) 中存在的误差点剔除。根据莱特准则,首先计算该组样本点集的算术平均值:
| $\bar{I}=\frac{1}{N}\sum\limits_{i=1}^{N}{l(i)};(i=1,2,...N)$ | (12) |
其次,计算标准差σ:
| $\sigma =\sqrt{\sum\limits_{i=1}^{N}{\frac{{{(l(i)-\bar{I})}^{2}}}{N-1}}};(i=1,2,...N)$ | (13) |
则该组数据的残差lb(i):
| ${{l}_{b}}(i)=l(i)-\bar{I};(i=1,2,...N)$ | (14) |
根据莱特准则,若lb≤-3σ或者lb≥3σ,则i点表示的点为粗大误差点,利用相关函数将该点在待拟合曲线上剔除。然后运用最小二乘法对新的待拟合曲线进行椭圆拟合。重复上述步骤,直至l(i)的残差lb(i)均在|3σ|内,表示该组数据中没有误差点,最终拟合的椭圆为最优椭圆。根据实验显示,基于此算法进行椭圆拟合,可以降低拟合误差,并且该算法也适用于不完整曲线的椭圆拟合。因为算法的计算量较少,在样本点数量为600~1000时,运行时间可以控制在10 ms内,可以满足检测生产线上速度为9 m/s以下的香烟圆度的要求。
3 算法测试 3.1 仿真测试本文提出的优化算法基于VS2013、OpenCV 2.4.8 平台进行开发。为了验证算法的正确性与有效性,使用OpenCV库函数cvEllipse(CvArr* img,CvPoint center,CvSize axes,double angle,double start_angle,double end_angle,CvScalar color,int thickness=1,int line_type=8,int shift=0) ,输出一个在像素坐标系下已知参数的局部二维椭圆,其参数为: center.x=300;center.y=150;a=150 px;b=100 px;θ=90°;startangle=30°;endangle=230°。
将已知参数的局部椭圆作为实验对象一;在对象一中加入毛刺点作为实验对象二,模拟结构光照射过程中产生的不可剔除的光噪点;在对象一长轴端加入噪声像素段作为实验对象三;模拟结构光在照射物体表面形成的连续误差像素段。 对三组实验对象分别用最小二乘法,基于莱特准则的优化算法进行椭圆拟合。两者拟合数据结果对比如表 1所示,椭圆拟合效果对比如图 3所示。
观察表 1的测试结果,两种拟合算法均可以对不整椭圆曲线进行拟合,并且两者均存在一定的拟合误差。当研究对象是标准曲线时,两者拟合结果没有很大差别,且准确率都很高,但当测试对象上存在无法剔除的毛刺点和其他连续噪声轮廓时,基于莱特准则的优化算法拟合效果优于最小二乘法。以表 1的数据为参考对象,莱特准则优化后的算法拟合精度比最小二乘法提高2%。在实验对象噪声点数量增加的过程中,与椭圆理论参数值相比,基于莱特准则的椭圆拟合算法已达到优化效果,验证了本算法的正确性与有效性。本文研究的待拟合曲线均为不规则曲线,实验结果也表明基于莱特准则的椭圆拟合优化算法更适用于不规则曲线。
| 表 1 仿真测试数据结果 Table 1 Data results of simulation testing |
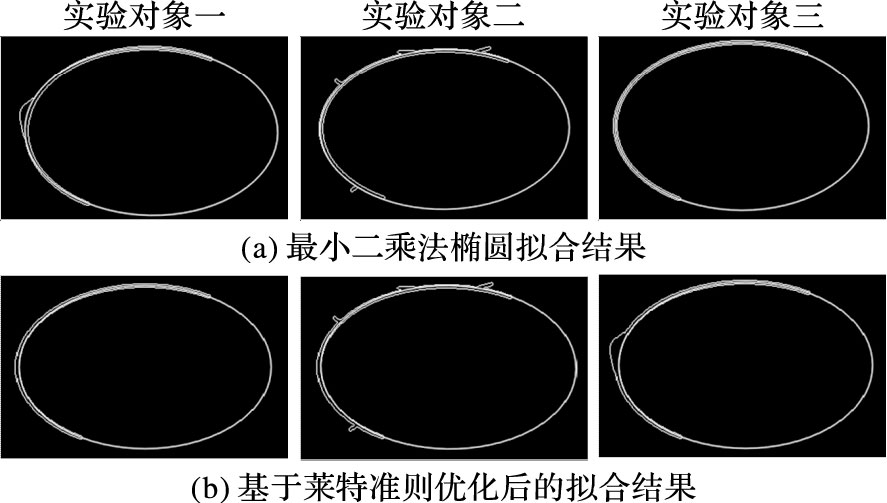
|
图 3 仿真测试椭圆拟合结果 Figure 3 Ellipse fitting results of simulation |
制造业中的视觉信息反馈能确定产品的形状、尺寸、姿态、位置、品质和类别是否合格,同时它具有非接触、全场测量、高精度等优点,不会给被检测物体加以任何干扰限制,因此非常适合检测在生产线上作业中的物体[15]。
在我国,烟草行业一直占有非常重要的地位,其税收是政府财政收入的重要来源之一。我国由于人口基数大,烟民多,烟草行业一直保持着八个世界第一的记录。香烟生产过程控制严格,产品质量要求高,其中香烟生产过程中烟条的圆度就是一项需要进行检测的指标,并且在以往的生产中也没有很好的在线检测方式。针对上述缺点,本文设计一套基于视觉信息的无接触式香烟圆度检测系统,该系统检测灵敏,检测结果稳定并且精确度高。
大多数的香烟在卷烟过程中,因卷纸一侧涂有胶水,需经过高温熨烫和机械压头轻压使卷纸两端部分重叠,形成圆筒状。所以在卷纸过程中,由于机械压头对烟条的压力作用,烟条在生产线上时其横截面并不是规则的圆形,而是一个近似于圆形的椭圆,其形状如图 4所示。
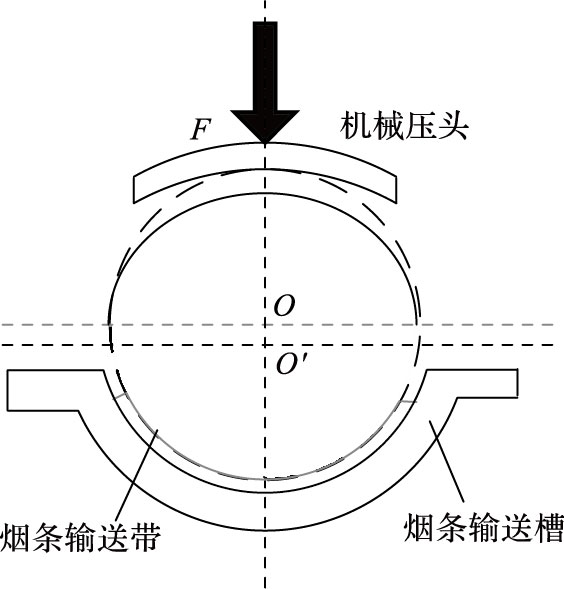
|
图 4 卷烟烟条的横截面示意图 Figure 4 Cross section of cigarette on production line |
香烟圆度表示香烟横截面接近理论圆的程度,根据圆度计算方法可知,如果可以实时检测到以O′为中心的椭圆的长轴和短轴的差值是否在允许范围内,就可判断机械压头是否在有效工作和香烟圆度是否合格。由于此检测工作是在卷烟完毕后进行,此时烟条并未剪断,所以相机不能在烟条横截面处拍摄。为了解决此问题,本文设计一套香烟圆度检测装置。
如图 5所示,结构光在烟条纵截面上方一定距离处以固定角度(此处θ=50°)照射在烟条上,形成光斑。工业相机进行图像抓取,经过图像去噪等基本处理,得到月牙状光斑。
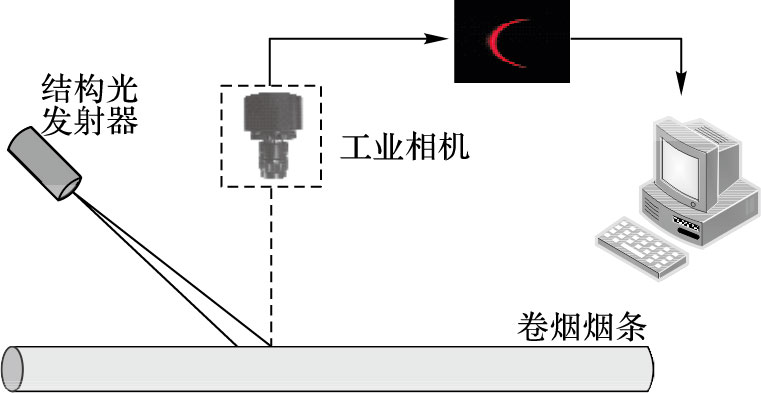
|
图 5 香烟圆度检测系统示意图 Figure 5 System diagram for roundness measurement of cigarette |
用莱特准则优化算法对月牙光斑进行椭圆拟合,结果如图 6所示,其中椭圆部分是拟合结果,月牙形是拟合曲线,同时得到椭圆长轴a、短轴b。对合格香烟进行多次检测,完成数据标定与误差补偿,标定结束后对生产线上的香烟进行圆度检测。
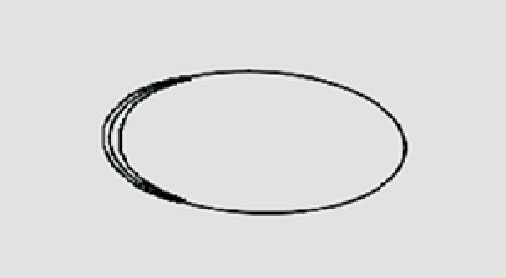
|
图 6 优化算法拟合结果 Figure 6 Ellipse fitting results of improved algorithm |
由图 7可知:
| $h=a\sin \theta =a\sin {{50}^{\circ }}$ | (15) |
| $Δh=b-h$ | (16) |
由圆度定义可知,Δh为被检测烟条的圆度值。通过判断一个检测周期内Δh的平均值是否在有效区域内,可以判断烟条加工是否合格。
本项目与湖南常德卷烟厂合作,对其生产的芙蓉牌系列香烟进行圆度检测。以软蓝芙蓉王为例,产品规格:直径8 mm、长度84 mm、圆度0.3 mm。项目所用工业相机型号WY3500,像素2 952×1 944,每秒曝光10次。在检测过程中,相机拍摄焦距固定,光斑经过摄像机采集后映射到图像中,假设图像不存在畸变,则像素尺寸与实际尺寸之间存在着固定的比例关系,经过测试,比值K=23.10。
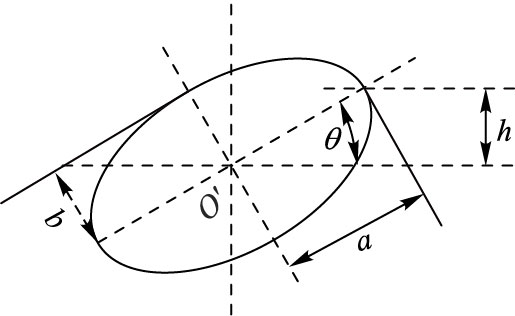
|
图 7 圆度检测数据分析示意图 Figure 7 Analysis of roundness measurement data |
表 2为在烟条运行速度为7.58 m/s的环境下,10 min内对烟条圆度进行检测的结果,共6 000组数据,为统计方便,现以每400组数据的平均值为一组,共15组数据,如表 2所示。
| 表 2 烟条圆度在基于莱特准则优化后的视觉检测系统中测试结果 mm Table 2 Roundness measurement data of cigarette based on Letts criterion mm |
对表 2中得到的15组Δh进行数据分析,可知Δh在此10 min内均在圆度的允许值范围内,说明此时间段内烟条圆度合格。经过多次现场调试,目前该方法可以较好地检测香烟圆度。但因为视觉信息对光噪声和外界震动特别敏感,所以该系统对外界环境要求较高。在系统测试阶段,将用最小二乘法视觉检测系统检测合格的香烟烟条与用莱特准则优化后的视觉检系统检测合格的烟条再次进行线下圆周检测。各取由最小二乘法检测香烟圆度合格的烟条和基于莱特准则优化后的检测合格的烟条10根为研究对象,并将每根烟条平均分成10小段,每小段由人工提取5个不同的测量点进行圆周检测,并求取5个圆周的平均值,与圆度允许范围作比较判断其是否合格,最终统计两个算法下,10根烟条每小段的平均合格率,结果如表 3所示。
| 表 3 香烟圆度线下10根烟条的检测结果 % Table 3 Offline roundness measurement results of 10 cigarettes % |
实际检测结果表明,最小二乘法检测系统中出现的香烟合格率要比优化过后的视觉检测系统中出现的合格率低。换言之,在湖南常德卷烟厂项目中,当卷烟烟条以7.58 m/s的速度运行,环境光噪声和外界震动较小且一定的情况下,优化过后的视觉检测系统在线测量香烟圆周的准确率可以达到95%以上。此优化算法和该套香烟圆度视觉检测系统很好地解决了我国自主香烟参数检测设备研发中遇到的香烟在线检测精度不高、检测速度慢等问题。
4 结语椭圆拟合算法在图像处理中具有广泛的应用,同时也是图像处理技术中最重要的内容之一。现已有很多对椭圆拟合进行优化的算法,但大部分算法复杂,拟合周期较长,无法满足现代工业中高速检测的要求。为了改善此情况,本文提出了一种基于莱特准则的椭圆拟合优化算法,在最小二乘法的基础上,用莱特准则剔除误差点,得到精度更高、运算时间较少的拟合椭圆,并将该算法运用于香烟圆度检测中,并设计一套基于视觉信息的检测设备,为我国自主香烟检测设备提供了一种新思路。
| [1] | 赵光明.机器视觉系统中的椭圆检测算法研究[D].武汉:华中科技大学,2009:1-5. ( ZHAO G M. Study on ellipse detection algorithm in machine vision system[D]. Wuhan:Huazhong University of Science and Technology, 2009:1-5. ) |
| [2] | 闫蓓, 王斌, 李媛. 基于最小二乘法的椭圆拟合改进算法[J]. 北京航空航天大学学报, 2008, 34 (3) : 295-298. ( YAN B, WANG B, LI Y. Optimal ellipse fitting method based on least square[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34 (3) : 295-298. ) |
| [3] | 韩建栋, 杨红菊, 吕乃光. 视觉测量中椭圆自动检测与定位方法[J]. 计算机工程与应用, 2011, 47 (17) : 169-171. ( HAN J D, YANG H J, LYU N G. Automated ellipse detection and location method on 3D visual inspection[J]. Computer Engineering and Applications, 2011, 47 (17) : 169-171. ) |
| [4] | YANG D L, BAI Q C, ZHANG Y L, et al. Eye location based on Hough transform and direct least square ellipse fitting[J]. Journal of Software, 2014, 9 (2) : 319-323. |
| [5] | 夏菁.椭圆拟合方法的比较研究[D].广州:暨南大学,2007:1-7. ( XIA J. Research on ellipse fitting method[D]. Guangzhou:Jinan University, 2007:1-7. ) |
| [6] | 陈海峰, 雷华, 孔燕波, 等. 基于最小二乘法的改进的随机椭圆检测算法[J]. 浙江大学学报(工学版), 2008, 42 (8) : 1360-1364. ( CHEN H F, LEI H, SUN Y B, et al. An improved randomized algorithm for detecting ellipses based on least square approach[J]. Journal of Zhejiang University (Engineering Science), 2008, 42 (8) : 1360-1364. ) |
| [7] | 张维光, 韩军, 周翔. 线结构光多分辨率测量系统数据拼接方法[J]. 仪器仪表学报, 2013, 34 (7) : 1441-1447. ( ZHANG W G, HAN J, ZHOU X. Data registration method for multiresolution measurement system with line structured light[J]. Chinese Journal of Scientific Instrument, 2013, 34 (7) : 1441-1447. ) |
| [8] | KURT O, ARSLAN O. Geometric interpretation and precision analysis of algebraic ellipse fitting using least squares method[J]. Acta Geodaetica et Geophysica Hungarica, 2012, 47 (4) : 430-440. doi: 10.1556/AGeod.47.2012.4.4 |
| [9] | 邹益民, 汪渤. 一种基于最小二乘的不完整椭圆拟合算法[J]. 仪器仪表学报, 2006, 27 (7) : 808-812. ( ZHOU Y M, WANG B. Fragmental ellipse fitting based on least square algorithm[J]. Chinese Journal of Scientific Instrument, 2006, 27 (7) : 808-812. ) |
| [10] | FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21 (5) : 476-480. doi: 10.1109/34.765658 |
| [11] | 朱新岩, 史忠科. 基于残差特性分析的野值检测与剔除方法[J]. 飞行力学, 2008, 26 (6) : 79-83. ( ZHU X Y, SHI Z K. Outlier detection method based on characteristic analyzing of residue[J]. Flight Dynamics, 2008, 26 (6) : 79-83. ) |
| [12] | LAGANIERE R. OpenCV2 Computer Vision Application Programming Cookbook[M]. Birmingham: Packt Publishing, 2011 : 143 -164. |
| [13] | Philipp Wagner. Machine learning with OpenCV2[EB/OL].[2016-03-10] . http://www.bytefish.de. |
| [14] | 章毓晋. 图像处理和分析[M]. 北京: 清华大学出版社, 1999 : 35 -36. ( ZHANG Y J. Image Processing and Analysis[M]. Beijing: Tsinghua University Press, 1999 : 35 -36. ) |
| [15] | 李龙, 何明一, 李娜. 椭圆拟合的圆环模板摄像机标[J]. 西安电子科技大学学报(自然科学版), 2010, 37 (6) : 1148-1154. ( LI L, HE M Y, LI N. Camera calibration based on the circular pattern and ellipse fitting[J]. Journal of Xidian University (Natural Science), 2010, 37 (6) : 1148-1154. ) |




