分级身份密码机制(Hierarchical Identity Based Cryptography,HIBC)具有标识产生公钥、密钥分级派生等特点,被广泛应用在云计算、延迟容忍网络等环境中[1-3]。HIBC批验签机制是指验签者能够对多个签名者的HIBC签名进行批量验签,其效率优于对其单独验签[4-6]。但是当批验签中存在错误签名时,将使得批验签失败,例如恶意节点发送虚假签名,因此需要采用错误签名筛选机制将错误签名快速筛选出来。
目前,针对批验签的错误签名筛选方法大致可以分为三类:拆分攻克方法[7]、指数测试方法[8]以及混合测试方法[9]。2010年,Matt[10]提出了一种混合测试算法——裁剪搜索(Triple Pruning Search,TPS)算法,分析表明TPS算法相对其他算法具有更高的运算效率。但是,TPS方法仅考虑了完全聚合的批验签方案,当将其应用到不完全聚合的HIBC批验签算法时,未能利用过程数值的重复可用性降低计算开销。本文针对上述问题,提出一种面向HIBC批验签的错误签名混合筛选算法(TPS for HIBC,TPSH),在TPS算法的基础上,利用先前计算数值参与后续计算步骤,从而进一步减少计算开销。为方便描述,本文以文献[5]中的HIBC批验签算法为例,对该TPSH算法进行描述。同时,本文算法仅需要少量改动即可应用于其他基于双线性对的批验签算法中[11-12]。
1 HIBC批验签算法简介文献[5]设计实现了一种HIBC批验签算法,能够对HIBC签名进行批验证,减少计算开销。算法包括初始化、私钥生成、签名、验签及批验签5个部分。
1) 初始化。令群G,GT的阶为p,双线性对e:G×G→GT。根密钥生成中心(Private Key Generator,PKG)选择α∈R Zp,P∈R G,设置P1=αP,随机选取P2,Pm,Pm′∈G;从群G中随机选取两个h元有序组Pu=(Pu,1,Pu,2,…,Pu,h),Pu′=(Pu′,1,Pu′,2,…,Pu′,h)。根PKG将主密钥αP2秘密保存,将公开参数〈P,P1,P2,Pm,P′m,Pu,Pu′〉安全分发给用户。
2) 私钥生成。用户ID=(ID1,ID2,…,IDk)的私钥可以通过根PKG以及所属子PKG产生,过程如下:令用户的子PKG节点身份标识为(ID1,ID2,…,IDk-1),对应的私钥d′=(d′0,d′1,τ′,v′,A′k,A′k+1,…,A′h,B′k,B′k+1,…,B′h)。选取t∈R ZP,用户ID的私钥生成如下:d0=d′0+A′k+IDkB′k+$t\sum\limits_{i=1}^{k}{{{V}_{i}}}$,d1=d′1+tP, τ=τ′+tPm,υ=υ′+tPm′,Ai=A′i+tPu,i,Bi=B′i+tPu′,i,其中,k+1≤i≤h。
3) 签名。假设用户ID=(ID1,ID2,…,IDk)对消息m签名,其私钥d=(d0,d1,τ,υ,Ak+1,Ak+2,…,Ah,Bk+1,Bk+2,…,Bh)=(αP2+r($\sum\limits_{i=1}^{k}{{{V}_{i}}}$),rP,rPm,rPm′,rPu,k+1,rPu,k+2,…,rPu,h,rPu′,k+1,rPu′,k+2,…,rPu′,h)。
令W=Pm+mPm′,随机选取s∈Zp,计算签名为σ=(S1,S2),其中:
| $\begin{align} & {{S}_{1}}={{d}_{0}}+\tau +m\upsilon +s(\sum\limits_{i=1}^{k}{{{V}_{i}}}+W)= \\ & \ \ \ \ \ \ \ \alpha {{P}_{2}}+{r}'(\sum\limits_{i=1}^{k}{{{V}_{i}}}+W) \\ \end{align}$ | (1) |
| ${{S}_{2}}={{d}_{1}}+sP={r}'P;{r}'=r+s$ | (2) |
4) 验签。验签方收到签名σ后通过式(3) 进行验证:
| $e(P,{{S}_{1}})=e({{P}_{1}},{{P}_{2}})e(\sum\limits_{i=1}^{k}{{{V}_{i}}}+W,{{S}_{2}})$ | (3) |
5) 批验签。令n个消息m1,m2,…,mn的签名为σ1,σ2,…,σn,其中σi=(Si,1,Si,2)。随机选取(δ1,δ2,…,δn)∈Zp,通过式(4) 对所有签名进行批验签:
| $\begin{align} & e(P,\sum\limits_{i=1}^{n}{{{\delta }_{i}}{{S}_{i,1}}})=e{{({{P}_{1}},{{P}_{2}})}^{(\sum\limits_{i=1}^{n}{{{\delta }_{i}}})}}\cdot \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \prod\limits_{i=1}^{n}{e(\sum\limits_{j=1}^{{{k}_{i}}}{{{V}_{i,j}}}+{{W}_{i}},{{\delta }_{i}}{{S}_{i,2}})} \\ \end{align}$ | (4) |
可以看出,对n个签名进行独立验签时需要2n次双线性对运算,而进行批验签时仅需n+1次,能够减少n-1次双线性对运算。但是采用批验签算法所面临的一个问题是,当批验签的签名中存在错误签名时,将使得批验签失败。因此,本文采用TPSH算法将其中的错误签名快速筛选出来。
2 TPSH算法TPSH算法的基本过程是将所有签名作为树叶构造平衡二叉树,利用拆分攻克与指数测试方法,测试整个树中是否存在错误签名数小于3的子树,若找到则返回该子树中所有错误签名的位置,之后继续在树中寻找错误签名数小于3的子树直到找出所有的错误签名。同时,算法利用相关计算中间值的关联性,优化计算过程,减少计算开销。
为了能够对上述HIBC批验签算法进行拆分攻克与指数测试,首先将HIBC批验签式(4) 转化成式(5) :
| $A=e(\sum\limits_{i=1}^{n}{{{B}_{i}},-P})\cdot \prod\limits_{i=1}^{n}{{{E}_{i}}}$ | (5) |
其中,Bi=δiSi,1,Ei=e(Di,Ti)·e(P1,P2)δi,Di=$\sum\limits_{j=1}^{{{k}_{i}}}{{{V}_{i,j}}}$+Wi,Ti=δiSi,2。
可以看出当A=1时,式(5) 等于式(4) 。相应的定义Ai为n个签名中第i个签名的独立验证公式,如式(6) 所示。当Ai=1时,说明第i个签名正确:
| ${{A}_{i}}=e({{B}_{i}},-P)\cdot {{E}_{i}}$ | (6) |
在式(6) 的基础上定义函数aj,[X],如式(7) 所示,其中:0≤j≤2,X表示树或者子树,Low(X)为X中最左侧叶子节点的序号,up(X)为X中最右侧叶子节点的序号。在树中,定义右侧叶子节点序号总是大于左侧叶子节点序号。函数aj,[X]将用于错误签名验证中的计算。当j=0且X为所有签名构成的树时,aj,[X]=A。
| $a_{j,[X]}^{{}}=e(\sum\limits_{i=low(X)}^{up(X)}{{{i}^{j}}{{B}_{i}},-P})\cdot \prod\limits_{i=low(X)}^{up(X)}{{{E}_{i}}^{{{i}^{j}}}}$ | (7) |
TPSH的具体验证过程如算法1所示,其流程与TPS相类似,不同之处在于H_Get0函数、H_Get1函数、H_Get2函数以及TPSHQuadSolver函数的实现方法。
算法1 TPSH算法。
输入:X //X是消息与签名列表
输出:错误签名列表。
1) if (X=Tr) then //X为树节点
2) a0,[X]=H_Get0(X)
3) if (a0,[X]=1) then return
4) a1,[X]=H_Get1(X)
5) z=Shanks(X)
6) if z≠0 then
7) print(mz,sz)
8) return
9) a2,[X]=H_Get2(X)
10) (z1,z2)=FastFactor(X)
11) if (z1≠0) then
12) Print(mz1,sz1),(mz2,sz2)
13) return
14) (SearchLeft,SearchRight)=TPSHQuadSolver(X,Left(X),Right(X),E[X]) //错误签名数≥3,进入子树查找
15) if (SearchLeft=true) then
16) TPSH(Left(X))
17) if (SearchRight=true) then
18) TPSH(Right(X))
19) if (X=Tr) then
20) PrintList()
21) return
在算法1中,首先进行初始化批验签第2) ~3) 行,通过H_Get0函数计算a0,[Tr],Tr表示所有签名所组成的树,并且保存中间相关计算变量供后续计算使用。由式(7) 可得式(8) :
| $\begin{align} & a_{0,[Tr]}^{{}}=e(\sum\limits_{i=low(Tr)}^{up(Tr)}{{{B}_{i}},-P})\cdot \prod\limits_{i=low(Tr)}^{up(Tr)}{{{E}_{i}}} \\ & \ \ \ \ \ \ \ =e(\sum\limits_{i=1}^{n}{{{B}_{i}},-P})\cdot \prod\limits_{i=1}^{n}{{{E}_{i}}} \\ \end{align}$ | (8) |
若a0,[Tr]=1则说明所有签名均正确,否则说明树中的错误签名总数(简记为w)大于0。
第4) ~8) 行用于测试树中w=1是否成立。首先通过H_Get1函数计算$a_{1,[Tr]}^{{}}=e(\sum\limits_{i=low(Tr)}^{up(Tr)}{i{{B}_{i}},-P})\cdot \prod\limits_{i=low(Tr)}^{up(Tr)}{{{E}_{i}}^{i}}$,其中$\sum\limits_{i=low(Tr)}^{up(Tr)}{i{{B}_{i}},}$、$\prod\limits_{i=low(Tr)}^{up(Tr)}{{{E}_{i}}^{i}}$能够通过调用H_Get0函数所保存的中间变量快速计算获得。其次,基于Shanks’s GSBS算法,采用指数测试方法,通过Shanks函数查找是否存在一个值z(1≤z≤N),使得a1,[Tr]=a0,[Tr]z,若存在,则w=1,z即错误签名的位置。例如,假设有4个签名,其中第3个签名为错误签名,则:$a_{1,[Tr]}^{{}}=e(\sum\limits_{i=1}^{4}{i{{B}_{i}},-P})\cdot \prod\limits_{i=1}^{4}{{{E}_{i}}^{i}}={{A}_{1}}\cdot {{A}_{2}}^{2}\cdot {{A}_{3}}^{3}\cdot {{A}_{4}}^{4}=A_{3}^{3}=a_{0,[Tr]}^{3}$。
如果未找到,则通过9) ~13) 行测试w=2是否成立。利用H_Get2函数计算$a_{2,[Tr]}^{{}}=e(\sum\limits_{i=1}^{n}{{{i}^{2}}{{B}_{i}},-P})\cdot \prod\limits_{i=1}^{n}{{{E}_{i}}^{{{i}^{2}}}}$。同理,基于指数分解法,利用FastFactor函数计算是否存在两个值i、 j,使得a2,[Tr]=a1,[Tr]i+ja0,[Tr]-ij。如果存在,则i、 j是错误签名的位置。否则说明w≥3,进入子树中继续寻找错误签名数小于3的子树。
第14) 行的TPSHQuadSolver函数用于查找子树中错误签名数是否小于3。其过程与TPSH主函数类似,不同之处在于计算右子树R的ɑj,[R]时,能够利用其父亲节点P及兄弟左节点L的计算结果减少计算开销,即aj,[R]=aj,[P]·aj,[L]-1。另外,若a0,[L]=a0,[P]≠1,则说明所有的错误签名均在左子树中,从而可以避免对右子树的测试。
算法2为H_Get0的实现算法,用于计算a0,[X]。1) ~11) 行用于计算a0,[Tr]。其中,VB0i以及EB0i为Bi、Ei的相关计算变量,需要保存在系统中供后续函数使用。12) ~35) 行用于在TPSHQuadSolver函数中计算子树中的a0,[X]值。令P为X的父亲节点,则当X为P的右子树时,根据算法流程,a0,[P]、a0,[L]均已计算,所以可直接获得a0,[X]=a0,[P]·a0,[L]-1,避免了双线对运算。当X为P的左子树时,能够通过先前保存的VB0i、EB0i快速计算出VB0s,u=$\sum\limits_{i=s}^{u}{{{B}_{i}}}$,$FB{{0}_{s,u}}=\prod\limits_{i=1}^{n}{{{E}_{i}}}$,之后通过一次双线性对运算计算出a0,[X]=e(WB0s,u,-P)·FB0s,u。
算法2 H_Get0(X)。
输入:X //X是消息与签名对列表
输出:a0,[X]的值。
1) if (X=Tr)then //X为根节点
2) VB0|X|=B|X| //Bi的定义见式(5) ,需要保存在缓存中
3) for i=|X|-1 downto 1 do
4) VB0i=VB0i+1+Bi//计算$\sum\limits_{i=1}^{n}{{{B}_{i}}}$值,需要保存在缓存中
5) for j=|X| downto 1 do
6) Ej=e(Dj,Tj)e(P1,P2)//计算Ei,其中e(P1,P2)为固定值,可提前计算
7) EB0|X|=E|X|
8) for i=|X|-1 downto 1 do
9) EB0i=EB0i+1·Ei//计算$\prod\limits_{i=1}^{n}{{{E}_{i}}}$,需要保存在缓存中
10) a0,[X]=e(VB01,-P)·EB01//计算$a_{0,[Tr]}^{{}}=e(\sum\limits_{i=1}^{n}{{{B}_{i}},-P})\cdot \prod\limits_{i=1}^{n}{{{E}_{i}}}$
11) return (ɑ0,[X])//第1) ~11) 行测试的是树,返回a0,[Tr]的结果,//如果是1,则说明正确,无错误签名。
12) P=Parent(X);L=Left(P);R=Right(P)//X为子树,定义P为X的父亲节点,P的相关数值已提//前计算并保存,L为P的左孩子节点,R为P的右孩子节点
13) if (X=R) then//X为P的右子树
14) a0,[X]=a0,[P]·a0,[L]-1//利用a0,[P],a0,[L]-1可直接获得a0,[X]
15) a0,[X]-1=a0,[P]-1a0,[L]//保存a0,[X]-1供后续计算使用
16) return (ɑ0,[R])
17) else if (X=L) then//X为P的左子树
18) s=lowbnd(X);u=upbnd(X)
19) WB0s,u=VB01-VB0u+1
20) FB0s,u=EB01·EB0u+1-1
21) if (s≠1) then
22) if (WB01,s-1) then//如果WB01,s-1已经计算过
23) WB0s,u=WB0s,u-WB01,s-1
24) else
25) WB01,s-1=VB01-VB0s
26) WB0s,u=WB0s,u-WB01,s-1
27) if (FB01,s-1) then//如果FB01,s-1已经计算过
28) FB0s,u=FB0s,u·FB01,s-1-1
29) else
30) FB01,s-1=EB01·EB0s-1
31) FB0s,u=FB0s,u·FB01,s-1-1
32) a0,[X]=e(WB0s,u,-P)·FB0s,u//计算出ɑ0,[X]
33) if (a0,[X]=a0,[P]) then
34) a0,[X]=a0,[P]-1
35) return(ɑ0,[X])
算法3为H_Get1的实现算法,用于计算a1,[X]。1) ~9) 行用于计算a1,[Tr],由于Ei值在计算a0,[Tr]中已经计算,并将相关值保存在EB0i中,所以避免了重新计算Ei所带来的双线性对运算,计算a1,[X]仅需一次双线性对运算。10) ~37) 行用于在TPSHQuadSolver函数中计算子树中的a1,[X]值,其方法与函数H_Get0中类似。另外,函数H_Get2用于计算a2,[X],其过程与函数H_Get1类似,在本文中不再描述。
算法3 H_Get1(X)。
输入:X,表示消息与签名对列表。输出:a1,[X]的值。
1) if (X=Tr) then //X为根节点,需要计算a0,[Tr]
2) VB1|X|=VB0|X| //VB0i值见H_Get0
3) for i=|X|-1 downto 1 do
4) VB1i=VB1i+1+VB0i
5) EB1|X|=EB0|X| //EB0i值见H_Get0
6) for j=|X|-1 to 1 do
7) EB1j=EB1j+1·EB0j
8) a1,[X]=e(VB11,-P)·EB1j
9) return(ɑ1,[X])
10) P=Parent(X);L=Left(P);R=Right(P);X′=Sibling(X) //X为子树,定义P为X的父亲节点,P的相关数值已提前//计算并保存,L为P的左孩子节点,R为P的右孩子节点,//X′为X的兄弟节点
11) if (a0,[X]=a0,[P]) then //P中的错误签名全部在X中,且w>1
12) a1,[X]=a1,[P]
13) a1,[X]-1=a1,[P]-1
14) return (a1,[R])
15) if (X=R) then //右孩子节点
16) a1,[X]=a1,[P]·a1,[L]-1
17) a1,[X]-1=a1,[P]-1a1,[L]
18) return (a1,[R])
19) else if (X=L) then //左孩子节点
20) s=lowbnd(X); u=upbnd(X)
21) WB1s,u=VB11-(VB1u+1+u·VB0u+1)
22) FB1s,u=EB11·EB1u+1-1
23) if (s≠1) then
24) if (WB11,s-1) then//如果WB11,s-1已经计算过
25) WB1s,u=WB1s,u-WB11,s-1
26) else
27) WB11,s-1=VB11-(VB1s+(s-1) VB0s)
28) WB1s,u=WB1s,u-WB11,s-1
29) if (FB11,s-1) then
30) FB1s,u=FB1s,u·FB11,s-1-1
31) else
32) FB11,s-1=EB11·EB1s-1
33) FB1s,u=FB1s,u·FB11,s-1-1
34) a1,[X]=e(WB1s,u,-P)·FB1s,u //计算出a1,[X]
35) if (a1,[X]=a1,[P]) then
36) a1,[X]=a1,[P]-1
37) return(a1,[X])
相对于原始的TPS算法而言,TPSH在计算aj,[X]时,利用Ei等中间值参与计算,并通过轻量级GT域上的乘法运算代替复杂双线性对运算,减少了aj,[X]的计算开销,提高了计算效率。
3 算法分析与比较本章将对算法效率与安全性进行分析与比较。首先对TPSH算法的效率进行分析与比较。为方便比较,令|Tr|表示所有进行批验证的签名数量,TA表示G上的加法运算,TT表示GT上的乘法运算,TP表示双线性对运算。
TPSH要求初始化批验签时,采用小指数测试方法。首先包括测试签名树Tr中所有签名元素是否在G中,接着计算a0,[Tr]。如果a0,[Tr]=1,则说明所有签名正确;如果a0,[Tr]≠1,则将计算中的所有Bi及Ei的相关计算变量VB0i,EB0i保存。另外,调用H_Get1计算a1,[Tr]及调用H_Get2计算a2,[Tr]的开销均为:|Tr|·(TA+TT)+TP。
下面给出筛选错误签名的具体开销。
1) 若错误签名数w=1,则TPSH的开销(不包括初始批验证)为一次a1,[Tr]计算,计算开销为|Tr|·(TA+TT)+TP,加一次成功的Shanks(Tr)运算,开销为$(4\sqrt{|Tr|}/3)\cdot {{T}_{T}}$。
2) 若w=2,则计算开销包括两次H_GET运算,一次失败的Shanks(Tr)运算,一次成功的FastFactor(Tr)运算,总计算开销为2(|Tr|·(TA+TT)+TP)+$2\sqrt{|Tr|}$TT+(11/4) |Tr|TT。
3) 当w>2时,计算开销包括两次H_GET运算,一次失败的Shanks(Tr)运算,一次失败的FastFactor(Tr)运算,总计算开销为2(|Tr|·(TA+TT)+TP)+$2\sqrt{|Tr|}$TT+(9/2) |Tr|TT,同时还包括调用递归函数TPSHQuadSolver时所产成的计算开销R(w,M),其与TPS算法中的TPSQuadSolver函数的计算开销相同,在此不再详细给出。
将本文的TPSH算法与独立测试、通用折半拆分(Generalized Binary Splitting,GBS)算法[13]、指数测试算法[8]以及TPS算法[10]进行比较:独立测试表示对各签名依次进行测试,为基准测试方案;GBS算法属于组测试技术,当错误签名数较小时,该算法的性能优于其他组测试技术。由于该算法需要在运算前给出错误签名w的估计值dw,估计值dw的正确性将影响算法的计算性能,在此处取GBS算法的最优值,即令错误签名值估计值与实际值一致(dw=w);指数测试方法通过在算法中增加指数,能够快速定位错误签名位置;TPS算法为TPSH的原始未改进方案。
依据文献[14]统计各操作的开销,令群的阶r为160 b,椭圆曲线E定义在域Fp上,p为160 b。在计算比较中,以域Fp上的乘法运算为单位(简记为t),并且采用双线性对成对运算(double pairing),各项密码的平均单次计算时间分别为:TP=7013t,TT=15t,TA=11t。
性能分析主要比较在不同批验签与错误签名数量的情况下,各方案的单次平均计算开销,分析比较结果如图 1所示。
|
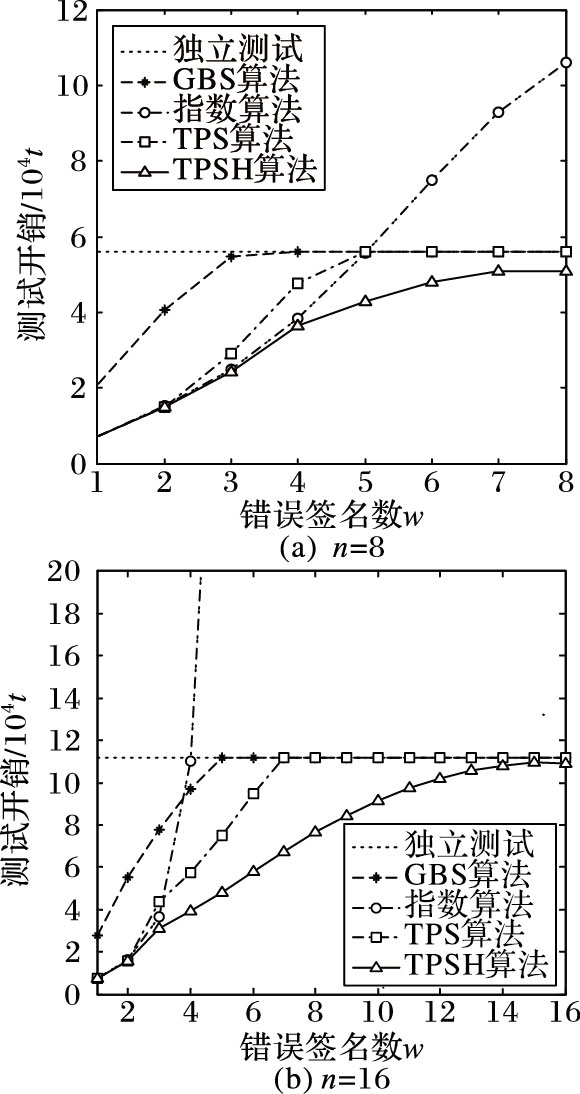
图 1 算法单次平均计算开销的比较 Figure 1 Comparison of average computing costs for single test |
在图 1(a)中,设置一次批验签的签名数量n=8。可以看出:当错误签名总数w=2,TPSH算法的单次平均计算开销与指数测试算法及TPS算法大体相同,其主要原因是当w <3时,3种算法均使用相同的指数测试方法。但是当w≥3时,TPSH的单次平均计算开销小于上述两种算法,其原因是:指数测试方法的计算开销随着w成指数增长,所以当w≥3后开销上升变快;TPS算法在测试本文HIBS算法时,由于未能利用先前双线性对计算数值参与后续计算步骤,从而导致计算开销增大;而本文的TPSH算法充分考虑HIBS算法的特点,通过划分子树进行指数测试,避免了计算开销的指数增长。同时,通过相关计算中间值的关联性,采用GT乘法运算代替双线性对运算,进一步减少了计算量,因此计算开销较小。另外,不管错误签名总数w为何值,TPSH算法的计算开销均小于独立测试及GBS算法。
在图 1(b)中,设置批验签的签名数量n=16,TPSH算法受签名数量n的影响不大,其性能依然优于其他算法。另外,可以看出在各算法中,指数测试方法受批验签数量及错误签名数量的影响最大。综上所述,TPSH的计算开销受批验签数量及错误签名数量的影响较小,当w≥3时,TPSH的计算开销小于独立测试、GBS算法、指数算法以及TPS算法。
在安全性方面,由于本算法主要用于提高HIBC算法中批验签判断式的计算效率,所以其安全性依赖于HIBC批验签算法自身的安全性。
4 结语本文针对HIBC批验签中的错误签名筛选问题,设计实现了一种错误签名混合筛选算法TPSH。该算法利用拆分攻克、指数测试以及中间值关联特性简化了错误签名的筛选计算,与现有的独立测试、GBS算法、指数算法以及TPS算法相比计算开销更小。下一步,将研究如何对TPSH进行形式化安全证明以及应用TPSH算法提高云计算的接入认证效率。
| [1] | KALYANI D, SRIDEVI R. Survey on identity based and hierarchical identity based encryption schemes[J]. International Journal of Computer Applications, 2016, 134 (14) : 32-37. doi: 10.5120/ijca2016908158 |
| [2] | 田俊峰, 孙可辉. 基于HIBC的云信任分散统一认证机制[J]. 计算机研究与发展, 2015, 52 (7) : 16660-16671. ( TIAN J F, SUN K H. Trust distributed based authentication mechanism using hierarchical identity based cryptography[J]. Journal of Computer Research and Development, 2015, 52 (7) : 16660-16671. ) |
| [3] | FIDA M R, ALI M, ADNAN A, et al. Region based security architecture for DTN[C]//Proceedings of the 2011 Eighth International Conference on Information Technology:New Generations. Piscataway, NJ:IEEE, 2011:387-392. |
| [4] | ZHU H J, LIN X D, LU R X, et al. An opportunistic batch bundle authentication scheme for energy constrained DTNs[C]//Proceedings of the 2010 IEEE Conference on Computer Communications. Piscataway, NJ:IEEE, 2010:1-9. |
| [5] | 徐国愚, 陈性元, 杜学绘. 大规模延迟容忍网络中基于分级身份签名的认证方案研究[J]. 电子与信息学报, 2013, 35 (11) : 2615-2622. ( XU G Y, CHEN X Y, DU X H. An authentication scheme using hierarchical identity based signature in large-scale delay tolerant networks[J]. Journal of Electronics & Information Technology, 2013, 35 (11) : 2615-2622. ) |
| [6] | NOISTERNIG M, HOLLICK M. Efficient solutions for the authenticated fragmentation problem in delay- and disruption-tolerant networks[C]//Proceedings of the 17th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems. New York:ACM, 2014:177-185. |
| [7] | LAW L, MATT B J. Finding invalid signatures in pairing based batches[C]//Proceedings of the Eleventh IMA International Conference on Cryptography and Coding. Berlin:Springer, 2007:35-53. |
| [8] | LEE S, CHO S, CHOI J, et al. Batch verification with DSA-type digital signatures for ubiquitous computing[C]//Proceedings of the 2005 International Conference on Computational and Information Science. Berlin:Springer, 2005:125-130. |
| [9] | MATT B J. Identification of multiple invalid signatures in pairing-based batched signatures[C]//Proceedings of the 2009 International Workshop on Public Key Cryptography. Berlin:Springer, 2009:337-356. |
| [10] | MATT B J. Identification of multiple invalid pairing-based signatures in constrained batches[C]//Proceedings of the 2010 International Conference on Pairing-Based Cryptography. Berlin:Springer, 2010:78-95. |
| [11] | WESOLOWSKI M. Batch verification of elliptic curve digital signa-tures[D]. Waterloo, Ontario:University of Waterloo, 2015:51-88. |
| [12] | AKINYELE J A, GREEN M, HOHENBERGER S, et al. Machine-generated algorithms, proofs and software for the batch verification of digital signature schemes[J]. Journal of Computer Security, 2014, 22 (6) : 867-912. doi: 10.3233/JCS-140507 |
| [13] | ZAVERUCHA G M, STINSON D R. Group testing and batch verification[C]//Proceedings of the 2009 International Conference on Information Theoretic Security. Berlin:Springer, 2009:140-157. |
| [14] | GRANGER R, PAGE D, SMART N P. High security pairing-based cryptography revisited[C]//Proceedings of the 2006 International Algorithmic Number Theory Symposium. Berlin:Springer, 2006:480-494. |




