自适应滤波算法广泛应用于系统辨识、网络回声消除等通信领域[1]。常用自适应算法有最小均方(Least Mean Square,LMS)算法、最小二乘(Recursive Least Square,RLS)法和仿射投影算法(Affine Projection Algorithm,APA)等。LMS算法由于其计算量小且易于实现而被广泛应用。在工程应用中,很多待辨识未知系统的冲激响应具有明显的稀疏特性,例如冲激响应往往长达数百的声学回声信道,只有很少的非零系数,是典型的单聚类稀疏信道[2]。块稀疏自适应算法利用稀疏先验知识提高算法收敛速度与稳态性能,插入相同分组长度的自适应抽头权重矢量的混合l(2.0) 范数惩罚因子到代价函数中[3],考虑到归一化,块稀疏归一化最小均方(Block Sparse-Normalization Least Mean Square,BS-NLMS)算法步长应除以输入矢量l2范数的平方与一个小的正常数之和。小的正常数是为了避免发生除零运算。但是BS-NLMS算法的推导是基于干扰噪声是高斯噪声的情况下,但是,在非高斯噪声情况下,该算法不具有抗冲激噪声干扰性能。
针对非高斯冲激噪声,文献[4-6]中算法的推导是基于最大相关熵函数准则,相关熵函数可视为局部相关性测量函数,因此,其比传统的基于全局相关性测量的自适应算法具有更好的抗冲激特性,但是固定步长的方案不能满足工程实践的需求。文献[7-8]分析了基于鲁棒统计思想的M评估(最大似然型)方法,该算法基于Huber损失函数在线估计阈值,此类算法计算复杂度高。在对抗冲激问题进行深入研究的基础上,本文提出了基于反双曲正弦的改进型块稀疏归一化最小均方(Improved Block Sparse-Normalization Least Mean Square,IBS-NLMS)算法。该算法代价函数在输出错误较小时具有l(2,0) 范数特性,而在输出错误较大时由于代价函数导数趋于零矢量而停止了滤波器系数更新。
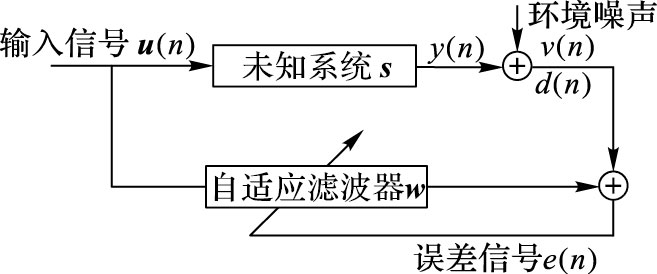
1 IBS-NLMS自适应滤波算法本文基于如图 1所示系统识别模型[9]进行分析,假设自适应未知系统s(n)=[s0(n),s1(n),…,sL-1(n)]T,滤波器的第n次迭代输入u(n)=[u(n),u(n-1) ,…,u(n-L+1) ]T,抽头长度为L,滤波器的未知系统期望信号输出d(n)表示为d(n)=uT(n)s(n)+v(n),加性噪声v(n)服从零均值、方差为σ2的高斯分布。第n次的估计误差迭代表示为e(n)=d(n)-xT(n)w(n),自适应滤波器抽头系数w(n)是自适应滤波器第n次迭代对s的估计。
|
图 1 系统辨识下自适应滤波器系统框图 Figure 1 Block diagram of adaptive filter for system identification |
算法的代价函数可表示成ξ(n)=e(n)2+λ‖w(n)‖2,0,λ为一个正因子,其中:
| ${\left\| w \right\|_{2,0}}\mathop = \limits^\Delta {\left\| {\;{{\left[ {{{\left\| {{w_{\left[ 1 \right]}}} \right\|}_2}\;{{\left\| {{w_{\left[ 2 \right]}}} \right\|}_2} \cdots {\kern 1pt} \,\,{{\left\| {{w_{\left[ {\text{N}} \right]}}} \right\|}_2}} \right]}^{\text{T}}}} \right\|_0}$ | (1) |
其中:w[i]=[w(i-1) P+1,w(i-1) P+1,…,wiP]T表示第i组的权系数向量w,N和P分别是滤波器阶数的分组数和每组长度。利用最陡下降法,可得自适应滤波器的更新公式为:
| $w(\mathrm{n}+1)=w(\mathrm{n})+\frac{\mu \mathrm{e}(\mathrm{n})u(\mathrm{n})}{u(\mathrm{n})u{{(\mathrm{n})}^{\operatorname{T}}}+\varepsilon }+\kappa \mathbf{g}\left( w(\mathrm{n}) \right)$ | (2) |
其中:g(w)[g1(w),g2(w),…,gL(w)]T,μ是用于调整误差和收敛速度的步长参数,ε是一个小的正常数,κ=μλ/2,α是一个正常数。
| ${{g}_{\mathrm{j}}}(w)\overset{\Delta }{\mathop{=}}\,\left\{ \begin{array}{*{35}{l}} 2{{\alpha }^{2}}{{\mathrm{w}}_{\mathrm{j}}}-2\alpha {{\mathrm{w}}_{\mathrm{j}}}/\left\| w\left[ \left\lceil \mathrm{j/p} \right\rceil \right] \right\|, & {} \\ {} & 0<\left\| w\left[ \left\lceil \mathrm{j/p} \right\rceil \right] \right\|\le 1/\alpha \\ 0, & 其他 \\ \end{array} \right.$ | (3) |
相比最小均方算法,式(2) 中额外的l(2,0) 范数约束改善了算法的稀疏特性。零范数约束条件下的未知系统参数解将更可能地趋于零向量,得到稀疏解,而2范数则可以解决输入信号自相关矩阵奇异造成的权系数不收敛问题。
1.2 基于非线性函数的IBS-NLMS算法为了改善算法在非高斯噪声下的抗冲激性,代价函数可重新改写为:
| $J\text{(}\mathsf{w})=E[arsinh({{(\alpha \left( e(n) \right)/\left\| \mathsf{u}(n) \right\|)}^{2}}/2\alpha )]$ | (4) |
其中:α>0用来控制代价函数梯度的系数;en/‖un‖表示均方误差;利用负梯度最陡下降法求w梯度,可得相应权系数更新公式如下:
w(n+1) =w(n)+
| $\begin{align} & \mathsf{w}(n+1)=\mathsf{w}(n)+ \\ & \mu \mathsf{u}(n)e(n)/\sqrt{{{\left\| \mathsf{u}(n) \right\|}^{4}}+{{\alpha }^{2}}e{{(n)}^{4}}}+\kappa \mathbf{g}\left( \mathsf{w}(n) \right) \\ \end{align}$ | (5) |
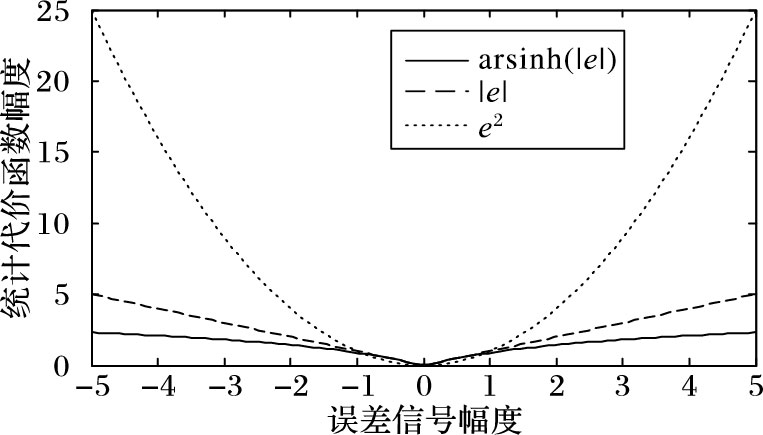
本文的步长衡量因子$1/\sqrt{1+{{\alpha }^{2}}e{{\text{(}\mathsf{n}\text{)}}^{4}}/{{\left\| \mathrm{u}\text{(}\mathsf{n}\text{)} \right\|}^{4}}}$满足文献[10]中提出的抗冲激条件。反双曲正弦函数arsinh是有界非线性函数,具有类sigmoid函数特性,其导数在开始时等于常数而随自变量增大后,导数趋于零,因此可用于降低冲激噪声影响,提高算法鲁棒性。对于小误差范围,通过观察如图 2误差代价函数的最陡下降梯度绝对值来观察收敛性能。算法的收敛速度与BS-NLMS算法一致,当非高斯噪声出现时,误差e(n)大幅度增加,算法抽头系数的增加量几乎为零,迭代几乎停止,从而消除了算法影响。本文所提出的算法在有冲激噪声时保持鲁棒性,同时在误差较小时保持低稳态误差和快收敛速度。
|
图 2 小误差下的代价函数 Figure 2 Cost function for small error |
本章主要分析IBS-NLMS算法在n趋于无穷时的收敛性能,权系数向量w(n)将逼近维纳-霍夫方程解w0=R-1P。为简化分析,作出了如下的假设。
假设1 输入信号u(n)是一个零均值高斯分布,自相关矩阵为R=E[u(n)uT(n)]的遍历过程。
假设2 假设文中加性噪声v(n)为高斯白噪声vg(n),利用文献[11]的变形高斯(Contaminated Gaussian,CG)噪声模型来估计冲激噪声,可建模为:
| $v\left( n \right)\text{ }={{v}_{g}}\left( n \right)\text{ }+{{v}_{im}}\left( n \right)$ | (6) |
无冲激噪声时v(n)=vg(n),当出现冲激噪声时,$v\left( n \right)\text{ }={{v}_{g}}\left( n \right)\text{ }+{{v}_{im}}\left( n \right)={{v}_{g}}\left( n \right)+b(n){{v}_{w}}\left( n \right)$和vw(n)满足零均值、方差分别为σg2和的独立同高斯分布。其中b(n)概率分布为Pr(b(n)=1) =pr和Pr(b(n)=0) =1-pr的伯努利随机序列。随机过程vg(n)和vw(n)可表示为$\sigma _{im}^{2}={{P}_{r}}\sigma _{w}^{2}$和$\sigma _{v}^{2}=\sigma _{g}^{2}+\sigma _{im}^{2}=\sigma _{g}^{2}+{{P}_{\operatorname{r}}}\sigma _{w}^{2}$。b(n)=0和b(n)=1时方差分别为σg2和$\sigma _{\Sigma }^{2}=\sigma _{g}^{2}+\sigma _{w}^{2}$。得出概率分布公式如下:
| $f(v)=\frac{1-{{P}_{r}}}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\sigma _{g}^{2}}}\exp (-\frac{{{v}^{2}}}{2\sigma _{g}^{2}})+\frac{{{P}_{r}}}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\sigma _{\Sigma }^{2}}}\exp (-\frac{{{v}^{2}}}{2\sigma _{\Sigma }^{2}})$ | (7) |
假设3 输入信号u(n),噪声v(n)和权系数向量w(n)统计独立。
定义向量c(n)为w0与w(n)之差c(n)=w0-w(n),则算法可写为:
| $\mathsf{c}\left( n\text{ }+\text{ }1 \right)\text{ }=\mathsf{ c}\left( n \right)-\frac{\mu \mathsf{u}(n)e(n)}{\sqrt{{{\left\| \mathsf{u}(n) \right\|}^{4}}+{{\alpha }^{2}}e{{(n)}^{4}}}}\text{+}\kappa \mathbf{g}$ | (8) |
对式(8) 两侧求期望,可得:
| $E\text{ }\left[ \mathsf{c}\left( n\text{ }+\text{ }1 \right) \right]\text{ }=\text{ }E\text{ }\left[ \mathsf{c}\left( n \right) \right]\text{ }-\mu \mathsf{H}$ | (9) |
E[·]表示对{v(n),c(n),u(n)}三者的期望值,其中E[·]记为E{v(n),c(n),u(n)}。
| $\mathsf{H=}{{E}_{\left\{ \mathsf{v}(n),\mathsf{c}(n),\mathsf{u}(n) \right\}}}\left[ \mu \mathsf{u}(n)e(n)/\sqrt{{{\left\| \mathsf{u}(n) \right\|}^{4}}+{{\alpha }^{2}}e{{(n)}^{4}}}-\kappa \mathbf{g} \right]= \\ {{E}_{\left\{ \mathsf{c}(n) \right\}}}[{{\mathsf{H}}_{c}}]$ | (10) |
其中,Hc可写为:
| ${{\mathsf{H}}_{c}}={{E}_{\left\{ \mathsf{v}(n),\mathsf{u}(n) \right\}}}\left[ \mu \mathsf{u}(n)e(n)/\sqrt{{{\left\| \mathsf{u}(n) \right\|}^{4}}+ \\ {{\alpha }^{2}}e{{(n)}^{4}}}-\kappa \mathbf{g}|\mathsf{c}(n) \right]$ | (11) |
由文献[12]可估计得到:
| ${{\mathsf{H}}_{c}}\approx \varphi '(\sigma _{e}^{2}(n))\mathsf{U\Lambda }{{\mathsf{D}}_{\Lambda }}{{\mathsf{U}}^{\text{T}}}\mathsf{c}(n)$ | (12) |
其中$\varphi '(\sigma _{e}^{2}(n))=\int_{-\infty }^{\infty }{(\varphi '(e)/\sqrt{2\pi }\sigma _{e}^{{}})}\exp (-({{\mathrm{e}}^{2}}/2\sigma _{e}^{2}))de$,$\sigma _{e}^{2}(n)={{\mathsf{c}}^{T}}(n)\mathsf{Rc}(n)+\sigma _{g}^{2}$,$\mathsf{R}=\mathsf{U\Lambda }{{\mathsf{U}}^{\text{T}}}$是自相关矩阵R的特征值分解,其中,Λ=diag(λ1,λ2,…,λL)是R的特征值组成的对角阵,U是R的特征向量构成正交矩阵。对角矩阵DΛ的第i个对角元素由Abelian积分方程得到。把式(10) 、(12) 代入式(9) 中,可得:
| $E\text{ }\left[ \mathsf{c}\left( n\text{ }+\text{ }1 \right) \right]\text{ }=(\mathsf{I}-\mu {{A}_{\varphi }}(\sigma _{e}^{2}(n))\mathsf{U\Lambda }{{\mathsf{D}}_{\Lambda }}{{\mathsf{U}}^{T}})\text{ }E\text{ }\left[ \mathsf{c}\left( n \right) \right]\text{ }$ | (13) |
把$\varphi '(\sigma _{e}^{2})$简写为${{A}_{\varphi }}(\sigma _{e}^{2}(n))$。令$\mathsf{C}(n)={{\mathsf{U}}^{T}}\mathsf{c}(n)$,$E\text{ }\left[ \mathsf{C}\left( n\text{ }+\text{ }1 \right) \right]\text{ }=(\mathsf{I}-\mu {{A}_{\varphi }}(\sigma _{e}^{2}(n))\mathsf{U\Lambda }{{\mathsf{D}}_{\Lambda }}{{\mathsf{U}}^{T}})\text{ }E\text{ }\left[ \mathsf{C}\left( n \right) \right]\text{ }$的一阶有限差分方程如下:
| $E\text{ }{{\left[ \mathsf{C}\left( n\text{ }+\text{ }1 \right) \right]}_{ i}}=(\mathsf{I}-\mu {{A}_{\varphi }}(\sigma _{e}^{2}(n)){{\lambda }_{i}}{{\mathrm{I}}_{i}}(\mathsf{\Lambda }))\text{ }E\text{ }{{\left[ \mathsf{C}\left( n \right) \right]}_{i}}$ | (14) |
在高斯白噪声的情况下,φ(e)≈e,所以,增加的迭代量$1/\sqrt{1+{{\alpha }^{2}}{{e}_{n}}^{4}/{{\left\| {{u}_{n}} \right\|}^{4}}}$对算法的稳态误差几乎无影响,所以由1-|μλiIi(Λ)|<1,可得μ<2/(λmaxIi_max(Λ))。因此,IBS-NLMS算法和BS-NLMS算法在无高斯噪声的情况一样,其稳态收敛范围0<μ<2/。
冲激噪声CG模型下,推导过程作出以下修改,首先$\mathsf{H}_{c}^{*}={{E}_{\left\{ \mathsf{v}(n),\mathsf{u}(n) \right\}}}\left[ \mu {{\mathsf{u}}_{n}}{{e}_{n}}/\sqrt{{{\left\| {{\mathsf{u}}_{n}} \right\|}^{4}}+{{\alpha }^{2}}{{e}_{n}}^{4}}-\kappa \mathbf{g}|c(n) \right]=$=$(1-{{P}_{r}}){{\mathsf{H}}_{g}}+{{P}_{r}}{{\mathsf{H}}_{\Sigma }}$,Hg和HΣ分别是{vg(n),c(n),u(n)}和{vΣ(n),c(n),u(n)}的期望值,根据式(12) 可得到相似表达式${{\mathsf{H}}_{g,\Sigma }}\approx {{\varphi }^{*}}(\sigma _{g,\Sigma }^{2}(n))\mathsf{U\Lambda }{{\mathsf{D}}_{\Lambda }}{{\mathsf{U}}^{\text{T}}}c(n)$,然后,方差改写为$\sigma _{eg}^{2}(n)={{\mathsf{c}}^{T}}(n)\mathsf{Rc}(n)+\sigma _{g}^{2}$和$\sigma _{e\Sigma }^{2}(n)={{\mathsf{c}}^{T}}(n)\mathsf{Rc}(n)+\sigma _{\Sigma }^{2}$,为同上文的推导表达一致,令${{\varphi }^{*}}(\sigma _{g,\Sigma }^{2}(n))$等于${{A}_{\varphi }}^{*}(\sigma _{e}^{2}(n))$,则${{A}_{\varphi }}^{*}(\sigma _{e}^{2}(n))=(1-{{P}_{r}})\varphi (\sigma _{eg}^{2}(n))+{{P}_{r}}\varphi (\sigma _{e\Sigma }^{2}(n))$,同式(13) 、(14) 的推导方法,得μ<2/Λ)]。
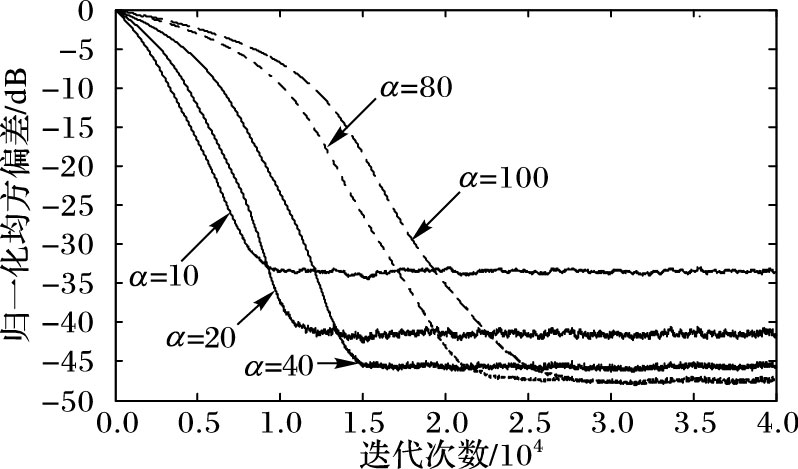
3 实验测试和结果分析本文包括3个仿真测试,第一个通过高斯噪声来验证本文所提算法特性,后面两个算法则分别验证了算法在冲激噪声和截断变化下的算法稳定性。随机产生长度为L=800的单聚类非零系数有限长冲激响应w,输入信号由零均值高斯随机信号通过一阶自回归模型T(z)=1/(1-0.7z)产生,高斯白噪声的输入信噪比设定为30 dB。用归一化均方偏差(Normalized Mean Square Deviation,NMSD)来度量自适应滤波器与待辨识系统的逼近程度,具体表达式为NMSD=10 lg(‖wi-w0‖22/‖w0‖22),所有仿真曲线均是通过50次独立实验求平均值获得。κ和P分别选择为1.55E-6和5。不同参数α值下的算法收敛及跟踪曲线NMSD变化曲线如图 3所示,当α相对较小时,随着α的增加而稳态误差减少,但是收敛速度却会随着α的继续增加而放缓,根据仿真结果,α=40将应用于后面的仿真实验中。
|
图 3 不同参数α值下的IBS-NLMS算法收敛及跟踪曲线 Figure 3 Convergence and tracking curve for IBS-NLMS algorithm with different α |
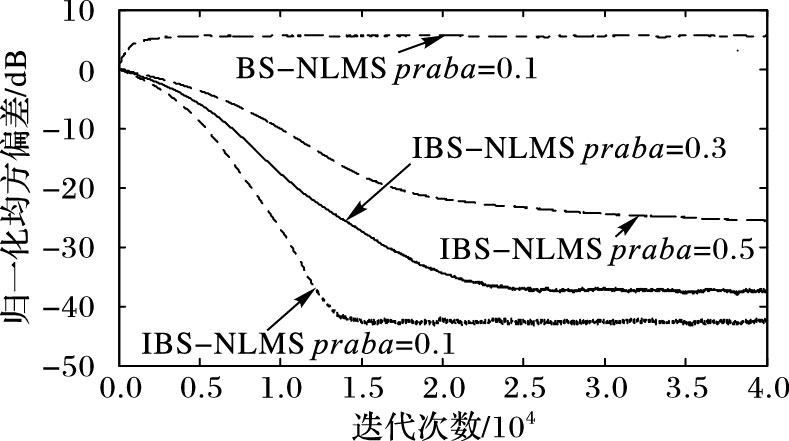
在实验中所选概率pr分别为0.1,0.3和0.5。NMSD变化曲线由图 4所示,IBS-NLMS算法在冲激噪声逐步增大的情况下,虽然误差增大,但是仍然保持了较高的稳定性,因而验证了IBS-NLMS算法对一般冲激噪声有很好的通用性和鲁棒性。冲激噪声模型为kiAi,Ai为零均值,功率为=1000σy2的高斯随机过程,ki为伯努利过程P[ki=1]=praba,其中,praba表示该过程中冲激噪声的出现概率。
|
图 4 不同概率冲激噪声下的算法NMSD学习曲线 Figure 4 NMSD learning curve with impulsive noise of probability praba |
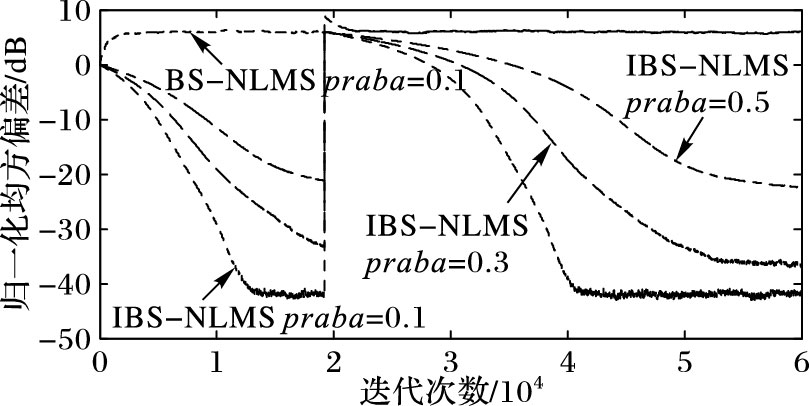
当冲激响应在第20000次迭代时从w突变为-w,算法滤波器参数与未知系统抽头系数的平均偏差变化曲线如图 5所示,测试算法包括IBS-NLMS和BS-NLMS,主要观测算法的收敛和跟踪性能,在冲激噪声下,BS-NLMS算法一开始就不收敛,而IBS-NLMS算法不仅收敛,而且在未知系统跳变后,算法很快跟上了系统的变化,主要是因为算法在这个时候的误差矢量的突然增大,算法的增加量趋于零向量,从而停止了算法的更新,可见,系统突变对本文所提出的IBS-NLMS算法未损失收敛速度和稳态误差性能。
|
图 5 系统冲激响应在第20000次迭代时从w变为-w Figure 5 Change of system impulse response from w to -w in iteration 20000 |
本文针对块稀疏系统辨识问题,提出了基于自适应的IBS-NLMS算法,用arsinh函数误差来替代均方误差。该算法使滤波器抽头权重增量在误差增大时趋于零矢量,显著地提高了算法鲁棒性同时不会影响在冲激噪声下的稳态误差。除此之外还推导了均值收敛过程中步长参数的上下界。仿真实验结果证明,提出的改进型算法在非高斯噪声下相较于BS-NLMS算法具有更快的收敛速度和更低的稳态误差。本文算法虽然提高了鲁棒性,但是计算复杂度还是很高,不利于实际应用中的实现,因此,如何有效地降低算法复杂度将会是下一步研究工作。
| [1] | HAYKIN S. Adaptive Filter Theory[M]. Upper Saddle River, NJ: Pearson Education, 2008 : 120 -180. |
| [2] | JIANG S, GU Y T. Block-sparsity-induced adaptive filter for multi-clustering system identification[J]. IEEE Transactions on Signal Processing, 2015, 62 (20) : 5318-5330. |
| [3] | LIU J, GRANT S L. Proportionate adaptive filtering for block-sparse system[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016, 24 (4) : 623-630. doi: 10.1109/TASLP.2015.2499602 |
| [4] | SHI L M, LIN Y. Convex combination of adaptive filters under the maximum correntropy criterion in impulsive interference[J]. IEEE Signal Processing Letters, 2014, 21 (11) : 1385-1388. doi: 10.1109/LSP.2014.2337899 |
| [5] | SHI L M, LIN Y, XIE X Z. Combination of affine projection sign algorithms for robust adaptive filtering in non-Gaussian impulsive interference[J]. Electronics Letters, 2014, 50 (6) : 466-467. doi: 10.1049/el.2013.3997 |
| [6] | LIU W, POKHAREL P P, PRINCIPE J C. Correntropy:properties and applications in non-Gaussian signal processing[J]. IEEE Transactions on Signal Processing, 2007, 55 (11) : 5286-5298. doi: 10.1109/TSP.2007.896065 |
| [7] | ZOU Y, CHAN S C, NG T S. Least mean M-estimate algorithms for robust adaptive filtering in impulse noise[J]. IEEE Transactions on Circuits and Systems, 2000, 47 (12) : 1564-1567. doi: 10.1109/82.899657 |
| [8] | AL-SAYED S, ZOUBIR A A. Sayed robust adaptation in impulsive noise[J]. IEEE Transactions on Signal Processing, 2016, 64 (11) : 2851-2865. doi: 10.1109/TSP.2016.2535239 |
| [9] | 金坚, 谷源涛, 梅顺良. 用于稀疏系统辨识的零吸引最小均方算法[J]. 清华大学学报:自然科学版, 2010, 50 (10) : 1656-1659. ( JIN J, GU Y T, MEI S L. Adaptive algorithm for sparse system identification:zero-attraction LMS[J]. Journal of Tsinghua University (Science and Technology), 2010, 50 (10) : 1656-1659. ) |
| [10] | 倪锦根, 马兰申. 抗脉冲干扰的分布式仿射投影符号算法[J]. 电子学报, 2015, 44 (7) : 1555-1560. ( NI J G, MA L S. Distributed affine projection sign algorithms against impulsive interference[J]. Acta Electronica Sinica, 2015, 44 (7) : 1555-1560. ) |
| [11] | TUKEY J W. A survey of sampling from contaminated distributions in contributions to probability and statistics[M]//OLKIN I. Contributions to Probability and Statistics. Palo Alto:Stanford University Press, 1960:448-485. |
| [12] | ZHOU Y, CHAN S C, HO K L, A new family of robust sequential partial update least mean M-estimate adaptive filtering algorithms[C]//Proceedings of the 2008 Asia Pacific Conference on Circuits and Systems. Piscataway, NJ:IEEE, 2008:189-192. |




