随着大规模和超大规模集成电路的问世,高性能计算(High Performance Computation,HPC)系统进入高速发展期,根据International Exascale Software Project(IESP)的研究报告[1]显示,HPC系统及其相关技术会持续发展。然而在实际部署与运行中人们发现,系统的高复杂性、高异构性导致HPC系统时刻面临着错误、故障和失效对于系统可用性保障上的挑战。Schroeder等[2]收集了两个世界级的高性能计算平台的故障数据,研究发现两个高性能计算平台每年的故障率在20~2000次即平均8.7 h就会发生一次故障,且故障率与系统规模呈正比。由此可见容错技术对于HPC系统变得越来越重要。
检查点是目前HPC系统领域通常采用的容错技术,通过在系统正常执行时周期性地保存其最新状态,在系统出现故障或失效等问题时,回滚到一致检查点位置之后重新恢复执行。采用检查点的方式可以有效节省回滚恢复时间,延长系统可用时间,但是由于检查点的设置与保存会占用一定的系统资源,因此检查点周期的优化直接关系到系统的容错能力与恢复效率。检查点周期是指系统设置并保存检查点的时间间隔,通过对系统状态与运行情况进行分析,选取合适的时间间隔进行检查点的设置与保存,一方面避免周期过小而导致检查点频繁设置保存对于系统资源的过度占用,一方面又避免周期过大导致系统回滚至过早的状态。检查点周期优化的研究可以为检查点协议提供最佳的性能,进而提高大规模HPC系统的可用性。
然而随着HPC系统结构变得越来越复杂,检查点周期优化也面临着状态分析复杂度增加等一系列的挑战。已有检查点周期优化的研究主要集中在不同的最优化算法[3-4]和HPC系统结构[5-6]上,却忽略了检查点结构对检查点性能的影响。HPC系统在实际工作中会受到许多外因诸如电压、环境温度的影响而产生系统性能抖动,这种性能抖动非常小,在理论研究过程中一般会忽略这种抖动而认为系统性能是稳定的,因此目前所有的检查点周期优化模型都是一种次优模型,即近似最优。本文首先将检查点周期优化抽象为一个非线性的检查点成本模型;然后通过分析分层检查点结构的特点,根据该模型对分层检查点的近似最优周期进行计算;最后通过仿真实验验证了本文所提模型的有效性。
1 相关工作检查点技术核心思想是将程序的最近运行状态保存至检查点内,并在故障发生时通过读取检查点使程序恢复至最近正常状态。因此,检查点技术的关键是要保证程序进程状态的一致性。不同检查点协议使用了不同的机制来保证进程状态的一致性,然而正是这些机制导致了检查点技术在大规模HPC系统中出现性能降级。经过检查点技术的多年发展,目前有三类非常成熟的检查点协议:非协同检查点协议、协同检查点协议和分层检查点协议。
分层检查点[7]是一种最近提出的检查点协议,它在结合协同检查点与非协同检查点优点的同时克服了两者的一些性能缺陷。分层检查点的核心思想是在分布式系统中将分布在不同的计算节点中的进程分组,其中进程组内使用协同检查点,在进程组间使用消息日志的非协同检查点。这样设计的优点是进程组之间相互独立,因此当某组进程在设置检查点的时候,其他组的进程能够并行地继续自己的计算工作,不会因为进程阻塞浪费执行时间,减少了同一时刻参与存储的进程的数目,从而增加每个参与进程的存储带宽,这样就减少了每个进程检查点设置的延时,并且,当某节点发生故障,故障节点可以单独恢复而不影响其他节点。
从检查点结构的角度进行检查点周期优化的研究才刚刚起步。Jin等[8]使用数值逼近方法对非协同检查点的周期优化进行了研究,但是忽略了消息日志机制对检查点读取速度的积极影响。Zheng等[9]从故障感知的角度对非协同检查点周期优化作出了研究,其研究内容没有考虑消息日志对检查点文件大小的影响。Wang等[10]使用马尔可夫链对协同检查点周期优化进行了研究,却没有研究检查点存储给系统带来的性能抖动。
2 分层检查点近似最优周期计算模型 2.1 检查点成本模型在HPC系统中,一个使用分层检查点的应用程序的执行过程可以用以下定义描述。
定义1 一个应用程序的执行过程是一个5元组{TIMEbase,μ,T,Delay,LOST},其中,T、Delay都是有穷集合,并且
1) TIMEbase是应用程序的规模,即应用程序无开销(不设置检查点、无故障)的基础运行时间。
2) μ是运行平台的平均无故障时间。
3) T是检查点周期。
4) Delay是检查点延迟的集合,Delay={Delay1,Delay2,…,DelayN}。其中:N是设置检查点的次数,Delayi是存储检查点而消耗的时间,1≤i≤N。
5) LOST是故障损失时间,LOST={LOST1,LOST2,…,LOSTM},其中,M是故障发生次数。特别的,LOSTi=Fi+Di+Ri,Fi是故障发生到最近检查点的任务丢失时间,Di 是故障后停机时间,Ri是恢复花费的时间,0≤i≤M。
根据上述定义,可以发现一个应用程序在HPC系统中的执行时间除了与其规模相关之外,还与检查点延迟和故障损失时间相关。因此可以得到一个通用HPC系统环境下、使用分层检查点的应用程序的运行时间如式(1) :
| $TIME=TIM{{E}_{\text{base}}}+\sum\limits_{i=1}^{N}{Dela{{y}_{i}}}+\sum\limits_{j=0}^{M}{({{F}_{i}}+{{D}_{i}}+{{R}_{i}})}$ | (1) |
为了研究方便,不妨设C=E(Delayi)为检查点延迟的数学期望,则N≈TIMEbase/(T-C)。设Tlost为故障损失的数学期望,本文考虑任意时刻内发生故障的概率是相同的,因此Tlost=E(LOSTi)=T/2+D+R。将上述等式代入式(1) 可得式(2) :
| $\begin{align} & TIME=TIM{{E}_{\text{base}}}+TIM{{E}_{\text{base}}}\left( T-C \right)\times C+ \\ & +M(T/2+D+R) \end{align}$ | (2) |
根据式(2) 可以发现,检查点延迟和故障损失是对立的,当周期T增大则故障损失增大;当周期T减小则检查点延迟增大。因此,这里定义一个概念“检查点成本”。
定义2 检查点成本表示为规模为TIMEbase、检查点周期为T的应用程序为了获得容错能力在执行时间方面增加的成本,即检查点延迟、故障损失在运行时间期望中占的比值。
根据定义2,可以得到式(3) 。结合式(1) 可以得到式(4) :
| $COST(T)=TIME(T)-TIM{{E}_{\text{base}}}/TIME(T)$ | (3) |
| $\begin{align} & COST(T)=COS{{T}_{\text{Delay}}}(T)+COS{{T}_{\text{Fault}}}(T)- \\ & COS{{T}_{\text{Delay}}}(T)COS{{T}_{\text{Fault}}}(T) \end{align}$ | (4) |
其中:COSTDelay(T)表示由检查点延迟增加的成本,COSTFault(T)表示由故障损失增加的成本。
在长度为T的周期内到达的故障数量可以抽象成一个参数是β=T/μ的泊松过程。为了确保每个周期只发生一个故障,本文给出一个约束条件使π≤0.03。因此,给出一个校正参数η使得T≤η μ。通过观察式(4) 可以周期优化问题被抽象成了一个周期为[C,η μ]的非线性优化,且经计算可得η=0.27。
2.2 检查点成本模型优化根据2.1节抽象出的非线性模型,本节针对分层检查点来进行模型优化。考虑一个在分布式并行环境下、紧耦合的应用程序。假设有G组进程,每组进程拥有q个处理器,且各组检查点在一个周期内顺序设置检查点。其中,设D(q)和R(q)分别为停机时间和恢复时间。
2.2.1 故障位置对故障损失时间的影响由于检查点需要被保存到稳定的存储器中,则检查点在存储阶段给应用程序的执行带来了延迟。本文引入参数α来表示这种影响,0≤α≤1。因此,一个检查点周期内应用程序的有效工作量如式(5) 所示:
| $WORK=T-(1-\alpha )C$ | (5) |
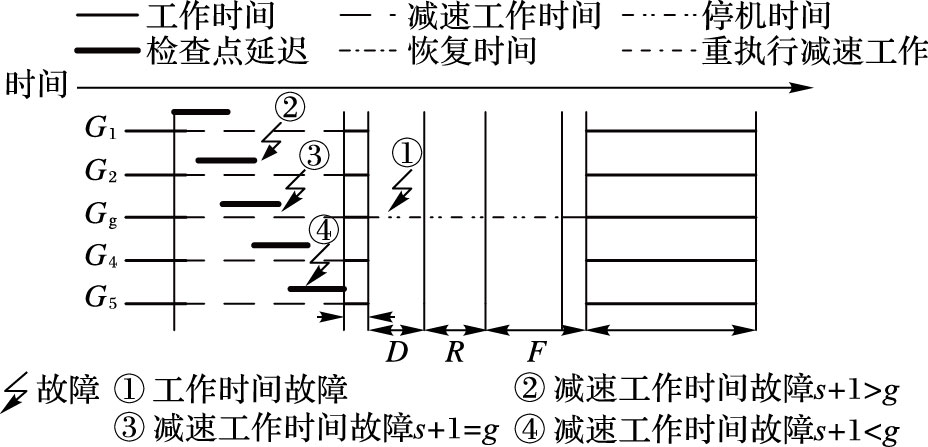
如图 1所示,故障可能发生的位置被参数α分为了工作时间和减速工作时间。其中,当故障发生在减速工作时间的时候,本文以进程组Gg的视角来看故障发生的位置有三种情况:组Gg设置检查点之前,组Gg设置检查点期间与组Gg设置检查点之后。
|
图 1 分层检查点可能故障位置 Figure 1 Possible fault position of hierarchical checkpoint |
根据图 1可以得到任务丢失时间F=Tlost+Tslow,工作时间和减速工作时间的Fw和Fs分别如式(6) 和式(7) 所示:
| $\begin{align} & {{F}_{w}}(q)=\left[ T-GC(q) \right]/T. \\ & \frac{1}{G}\sum\limits_{g=1}^{G}{\left[ (G-g+1)\alpha C(q)+\frac{T-GC(q)}{2} \right]} \end{align}$ | (6) |
| $\begin{align} & {{F}_{s}}(q)=\frac{GC(q)}{T}\frac{1}{{{G}^{2}}}\sum\limits_{g=1}^{G}{\left[ \sum\limits_{s=0}^{g-2}{(G-g+s+2)\alpha C(q)+} \right.} \\ & T-GC(q)+G\alpha C(q)+T-\alpha C(q)+C(q)/2+ \\ & \left. \sum\limits_{s=1}^{G-g}{(s+1)\alpha C(q)} \right] \end{align}$ | (7) |
式(6) 中第一项表示故障发生在工作时间内Fw的概率。由于分层检查点组间相互独立且顺序设置检查点,所以只需要重新执行组Gg和其后所有分组丢失的工作。因此,故障发生在工作时间的概率为(T-GC(q))/2,Tlost的数学期望为(T-GC(q))/2,Tslow的数学期望为(G-g+1) αC(q),其中1≤g≤G。
式(7) 中第一项表示故障发生在减速工作时间内Fs的概率。设当故障发生时已经有s组进程完成了检查点设置,即故障发生在s+1组且s+1正在设置检查点,其中0≤s≤g-1。图 1中减速工作时间内三种可能故障位置Tlost和Tslow的数学期望如式(6) 中大括号中每项所示。
结合式(5) ~(7) ,可以得到一个分层检查点成本公式(8) :
| $COS{{T}_{\text{hier}}}=\frac{T-WORK}{T}+\frac{1}{\mu }(D(q)+R(q)+F(q))$ | (8) |
分层检查点协议在组间使用了非协调检查点,其中的消息日志机制分别对程序的执行、重执行时间与检查点文件的大小造成了影响,从而影响了本文对检查点周期的优化。为了更精确地计算检查点周期,将引入三个新的参数来表示这种影响。
在进程被分成若干组的条件下,组间的事件日志必须存储在可靠的存储器中,这样才能在故障之后独立恢复指定组。然而存储事件日志为应用程序带来了额外开销,使用一个减速因子λ来表示这种影响,0<λ<1,典型的λ≈0.98[12]。相反,消息日志对故障之后的恢复有积极影响。因为组内消息存储在本地内存并在恢复的时候可以直接访问。因此,本文模型引入一个加速因子ρ,其中ρ的典型区间为[1, 2][13]。由上述两个影响因子的典型值区间可以看出,消息日志的有效载荷开销只占一个很小的百分比,对某些应用则可以缩短一半的恢复时间。
除此之外,由于组内消息被不断记录,消息日志机制同时也影响了检查点文件的大小,进而影响了分层检查点的检查点延迟。为了表示由于检查点文件增大对应用程序执行造成的影响,引入一个减速因子β,则C(q)=C0(q)(1+βλWORK)。其中β的计算公式随着应用程序的变化而变化。例如在一个二维三阶的模板计算中β=(2sp)/(9b3),其中sp是处理器的速度,b是模板计算中每个处理器计算矩阵的大小。可以得到一个优化后的检查点式(9) :
| $COS{{T}_{\text{hier}}}=\frac{T-\beta \lambda WORK}{T}+\frac{1}{\mu }(D(q)+R(q)+\frac{F(q)}{\rho })$ | (9) |
仿真实验环境由4台计算机组成一个分布式集群环境,计算机配置均为:Intel E4500 CPU,2 GB内存,500 GB硬盘。并行应用程序使用了NAS Parallel Benchmarks中的二维模板计算程序MG,同时使用Guermouche等[11]提出的HydEE作为分层检查点协议具体实现。故障注入程序的故障分布服Weibull分布,同时,相同节点在一个检查点周期内产生故障重叠概率不超过3%,即η=0.27,其参数如表 1所示。本文仿真环境下的具体参数如表 2所示。其中,λ和ρ的值分别参考文献[12]和文献[13]。根据仿真环境结合式(8) 计算可得不同平均无故障时间(Mean Time Before Fault,MTBF)条件下理论最优检查点与检查点成本如表 3所示。
| 表 1 故障注入程序参数 Table 1 Parameters of fault injection program |
| 表 2 仿真环境参数 Table 2 Parameters of simulation environment |
| 表 3 理论最优检查点周期与成本 Table 3 Theoretically optimal period and cost of checkpoint |
根据上文约束C≤T≤η μ,设应用程序的检查点周期分别在[0.82,32.4]和[0.82,64.8]两个区间中均匀分布。首先,在两种情况下运行程序MG,记录每个周期程序MG正常运行完成的时间并计算检查点成本COST,结果如图 2所示。其次,拟合实验结果曲线,与本文方法、文献[6]提出的模型进行对比,结果如图 3~4所示。
|
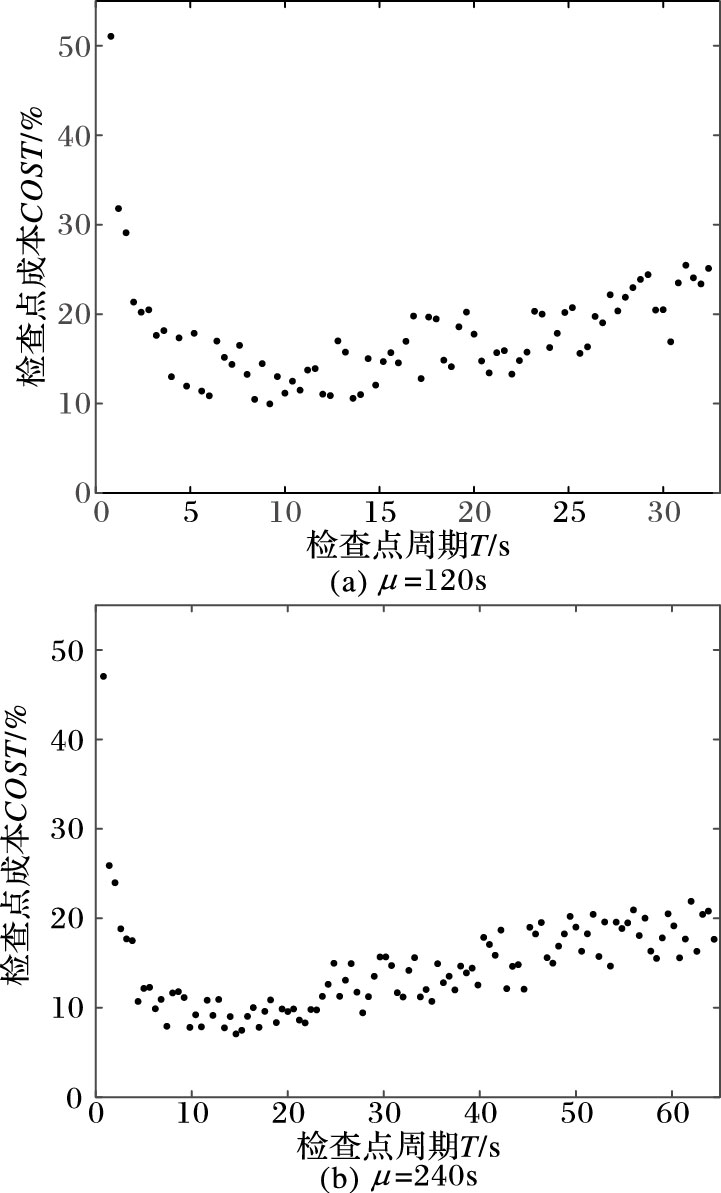
图 2 不同周期的检查点成本 Figure 2 Checkpoint costs for different periods |
|
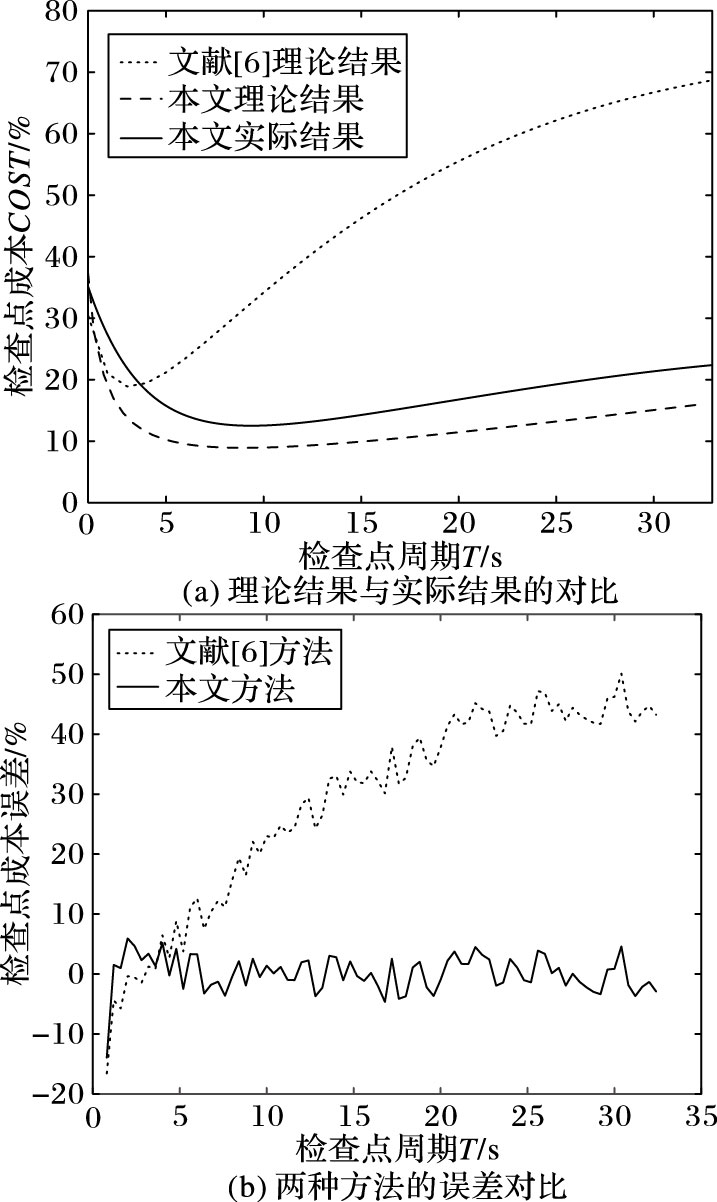
图 3 μ=120 s时的两种算法对比结果 Figure 3 Analysis of two methods (μ=120 s) |
|
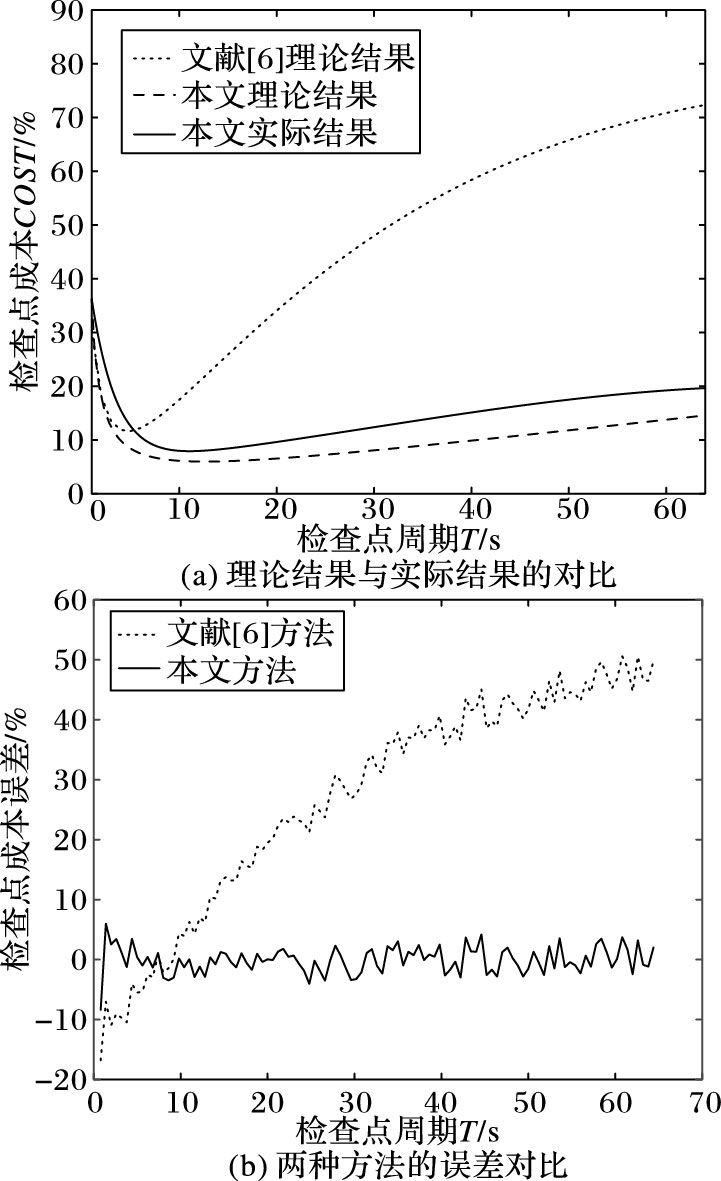
图 4 μ=240 s时的两种算法对比结果 Figure 4 Analysis results of two methods (μ=240 s) |
由图 2中点的分布可知,图 2(a)中周期T=9.2时检查点成本最COST小为9.9%;图 2(b)中,周期T=14.6时检查点成本最COST小为7.1%。在远离理论周期时,COST呈上升趋势。呈现上述分布规律的原因是:当周期T较小时,检查点周期内有效工作较少、检查点延迟较高。特别的,当周期T的值接近C时,应用程序几乎无法运行。当周期T较大时,应用程序在单个周期T内有效工作时间变长,故障概率增大,故障损失增大。除此之外,在大于理论周期值时,图 2呈现出明显的斜率不同,其原因是因为随着MTBF值的减小,单位时间内故障概率会增加,则故障损失的数学期望会变大。
由图 3(a)和图 4(a)的中的曲线可知,在仿真分布式环境、不同MTBF情况下,本文提出的周期计算模型更加符合实际情况。由图 3(b)和图 4(b)中的折线可知,本文提出的周期计算模型与实际运行情况的检查点成本误差在3%~5%变化,且MTBF较大情况下平均误差较小;而文献[6]提出的检查点周期检查点成本误差较大,在1%~50%变化。其中,图中横坐标为检查点周期,纵坐标为检查点成本误差。特别的,当文献[6]的优化模型在其最优检查点周期附近可以较好地计算检查点成本,但是在周期超过其理论最优值之后检查点成本快速升高,并且在MTBF较大的情况下升高速度更快。文献[6]的主要优点在于采用了马尔可夫链对分布式环境的检查点周期进行优化,较好地模拟了分布式环境中程序运行状态的转移;其主要缺点在于关注HPC系统结构的同时忽略了检查点协议对检查点成本的影响,将故障损失时间均摊至检查点延迟上,故而出现了图 3(b)和图 4(b)中高误差的现象。
根据仿真结果可以得出以下结论:1) 本文提出的检查点周期计算模型与理论近似最优检查点成本平均误差在5%以下,相对文献[6]所提方法的平均误差降低了20%;2) 检查点结构对检查点成本影响非常大,针对检查点结构对检查点周期进行优化可以得到更精确的结果。
4 结语针对提升检查点效率的问题,本文对检查点的周期优化的问题进行了研究,通过分析可能故障位置与消息日志对检查点成本造成的影响,提出了一种面向分层检查点的周期计算模型。仿真实验结果显示,本文提出的检查点周期计算模型与理论近似最优检查点成本平均误差在5%以下,相对传统检查点周期优化模型的平均误差降低了20%。目前混合容错技术越来越流行,故障预测与复制技术经常与检查点技术一起使用,下一步工作将尝试对结合故障预测及复制技术的检查点周期进行优化。
| [1] | DONGARRA J, BECKMAN P, MOORE T, et al. The international exascale software project roadmap[J]. International Journal of High Performance Computing Applications, 2011, 25 (1) : 3-60. doi: 10.1177/1094342010391989 |
| [2] | SCHROEDER B, GIBSON G A. A large-scale study of failures in high-performance computing systems[J]. IEEE Transactions on Dependable and Secure Computing, 2010, 7 (4) : 337-350. doi: 10.1109/TDSC.2009.4 |
| [3] | YOUNG J W. A first order approximation to the optimum checkpoint interval[J]. Communications of the ACM, 1974, 17 (9) : 530-531. doi: 10.1145/361147.361115 |
| [4] | DALY J T. A higher order estimate of the optimum checkpoint interval for restart dumps[J]. Future Generation Computer Systems, 2006, 22 (3) : 303-312. doi: 10.1016/j.future.2004.11.016 |
| [5] | 鄢喜爱, 杨金民, 田华. 双机容错系统中最佳检查点间隔的分析[J]. 计算机工程, 2007, 33 (5) : 283-285. ( YAN X A, YANG J M, TIAN H. Analysis of best checkpoint interval of duplicated fault tolerance system[J]. Computer Engineering, 2007, 33 (5) : 283-285. ) |
| [6] | GE Y, YANG Y, ZHU C. Study of the best checkpoint interval in the distributed simulation system based on virtualization technology[C]//AMCCE 2015:Proceedings of 2015 International Conference on Automation, Mechanical Control and Computational Engineering. Amsterdam:Atlantis Press, 2015:193-197. |
| [7] | 黄琼, 尚利宏, 周密, 等. 一种面向大规模并行系统的分组协同检查点算法[J]. 计算机研究与发展, 2010, 47 (S1) : 158-163. ( HUANG Q, SHANG L H, ZHOU M, et al. A group-based coordinated checkpointing algorithm for large-scale parallel system[J]. Journal of Computer Research and Development, 2010, 47 (S1) : 158-163. ) |
| [8] | JIN H, CHEN Y, ZHU H, et al. Optimizing HPC fault-tolerant environment:An analytical approach[C]//ICPP 2010:Proceedings of the 201039th International Conference on Parallel Processing. Piscataway, NJ:IEEE, 2010:525-534. |
| [9] | ZHENG Z, LAN Z. Reliability-aware scalability models for high performance computing[C]//CLUSTER' 09:Proceedings of 2009 IEEE International Conference on Cluster Computing and Workshops. Piscataway, NJ:IEEE, 2009:1-9. |
| [10] | WANG L, PATTABIRAMAN K, KALBARCZYK Z, et al. Modeling coordinated checkpointing for large-scale supercomputers[C]//DSN 2005:Proceedings of the 2005 International Conference on Dependable Systems and Networks. Piscataway, NJ:IEEE, 2005:812-821. |
| [11] | GUERMOUCHE A, ROPARS T, SNIR M, et al. HydEE:failure containment without event logging for large scale send-deterministic mpi applications[C]//IPDPS 2012:Proceedings of 2012 IEEE 26th International Conference on Parallel & Distributed Processing Symposium. Piscataway, NJ:IEEE, 2012:1216-1227. |
| [12] | BOUTEILLER A, HERAULT T, BOSILCA G, et al. Correlated set coordination in fault tolerant message logging protocols[C]//Euro-Par' 11:Proceedings of the 17th International Conference on Parallel Processing. Berlin:Springer, 2011:51-64. |
| [13] | BOUTEILLER A, BOSILCA G, DONGARRA J. Redesigning the message logging model for high performance[J]. Concurrency and Computation:Practice and Experience, 2010, 22 (16) : 2196-2211. doi: 10.1002/cpe.v22:16 |




