2. 华中科技大学 管理学院, 武汉 430074
2. School of Management, Huazhong University of Science and Technology, Wuhan Hubei 430074, China
LUO Qi, born in 1990, M. S. candidate. Her research interests include stock network, random matrix theory denoising.
HAN Hua, born in 1975, Ph. D., professor. Her research interests include analysis and evaluation of complex networks, economic control and decision.
GONG Jiangtao, born in 1990, M. S. candidate. His research interests include evaluation method for node importance.
WANG Haijun, born in 1970, Ph. D., professor. His research interests include management science and engineering, operation management.
资产收益之间的相关矩阵蕴含着金融资产间的交互相关作用,这对于资产组合选择和风险管理等重要的金融应用都是决定性的[1-2]。实际上,因时间序列长度的限制等原因,使得收益相关矩阵中含有噪声[3-4]。研究表明,当资产组合数目较多时,利用随机矩阵理论(Random Matrix Theory, RMT)可对相关矩阵中的大部分噪声进行有效去除。Laloux等[5]通过对S & P500的406只股票1991—1996年的数据进行分析从而区分出经验相关矩阵中的噪声信息,并认为最大特征值代表整个“市场模式”;Plerou等[6]详细研究了1000只美国证券在1994—1995年的30 min收益数据,定义了反比参率(Inverse Participation Ratio,IPR)来表示显著参与某一个特征向量的公司数量,得出了特征值谱边缘的反比参率较大,并对偏离特征值的意义进行了探究;Sharifi等[7]提出了基于RMT和特征向量Krzanowski稳定性的KR去噪法,并分析了将该方法用于组合风险优化的效果。然而,Utsugi等[8]在对东京证券交易所研究发现一些偏离预测的小特征值并不能完全由随机性进行解释,并表明随机性会对真实的相关性发生一定的排斥,类似于原子物理学中的“能级排斥”;Malevergne等[9]通过模拟与计算的对比分析说明了在RMT预测的主体特征谱中仍然存在着部分有效的相关信息;Kwapień等[10]通过不断变化100只美国股票的时间长度,发现当选择的时间较短时主体特征谱中并不完全是噪声信息;Dai等[11]对71只原油市场股票进行分析,研究得知最小特征值具有最大的相关系数,即表明小于预测值的特征值同样包含部分信息量。由此可知:噪声将随着研究资产的减小而下降,噪声与信息间的界定会存在一定程度的混淆,且小于预测值的特征同样包含一定的有效信息。本文考虑到蒙特卡罗方法就是结合实际情况构造与其吻合的统计实验概率模型,此过程包括使用随机数执行大量模拟和得到问题的近似解[12],为此,构建蒙特卡罗模拟修正的随机矩阵去噪方法,即利用蒙特卡罗模拟方法精确识别出小组合投资噪声特征值的范围,并将模拟去噪法应用于不同股票网络进行实证分析,从而验证模拟方法的有效性和优越性。
1 理论基础 1.1 随机矩阵理论记股票i(i=1, 2, …, N)的有效交易日价格序列为{Pi(1), Pi(2), …, Pi(L)}, L是股票i的有效交易天数,Pi(t)是股票i在第t个有效交易日的收盘价格,定义股票i的对数收益率(Logarithmic Return)如下:
| $ {G_i}\left( t \right) = \ln \left[{{P_i}\left( t \right)} \right] - \ln \left[{{P_i}\left( {t-1} \right)} \right] $ |
对任意两只股票i和j, 因有效交易价格序列不同,故在计算相关性时,取其共同有效交易日时间序列,则任意两只股票i和j之间的皮尔逊相关系数(Pearson Correlation Coefficient, PCC)为:
| $ {\rho _{ij}} = \frac{{\left\langle {{\boldsymbol{G}_i}{\boldsymbol{G}_j}} \right\rangle - \left\langle {{\boldsymbol{G}_i}} \right\rangle \left\langle {{\boldsymbol{G}_j}} \right\rangle }}{{\sqrt {\left( {\left\langle {{{\left( {{\boldsymbol{G}_i}} \right)}^2}} \right\rangle - {{\left\langle {{\boldsymbol{G}_i}} \right\rangle }^2}} \right)\left( {\left\langle {{{\left( {{\boldsymbol{G}_j}} \right)}^2}} \right\rangle - {{\left\langle {{\boldsymbol{G}_j}} \right\rangle }^2}} \right)} }} $ |
其中:〈·〉为统计平均,ρij∈[-1,1]。若ρij=-1表示两只股票完全负相关;若ρij=1表示两只股票完全正相关;若ρij=0表示两只股票不相关。从而可得到股票相关系数矩阵CN, 矩阵元素为ρij。
设随机矩阵R=(A×A′)/L, 其中A是由N个长度为L的独立的序列构成的随机矩阵,每个序列均服从N(0, 1)分布。矩阵R的统计性质是已知的,特别是当N→∞, L→∞, Q=L/N(>1)固定的情况下,R的特征值λ的分布函数P(λ)有如下解析形式:
| $ P\left( \lambda \right) = \frac{{Q\sqrt {\left( {{\lambda _ + } - \lambda } \right)\left( {\lambda - {\lambda _ - }} \right)} }}{{2\pi {\sigma ^2}\lambda }} $ |
其中:λ-+=σ2(1+Q-1±2
| $ P\left( V \right) = \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{V^2}}}{2}} \right) $ |
通过随机矩阵理论改进相关系数矩阵达到对金融系统去噪的RMT去噪方法种类很少,主要包括Laloux等[5]提出的LCPB法将小于λ+的市场特征值作为噪声,用噪声特征值的均值来代替噪声特征值,并保持新旧相关矩阵的迹不变;Plerou等[6]提出的PG+法用零替代相关矩阵的“噪声”特征值,并确保去噪前后矩阵的迹相等;Sharifi等[7]提出的KR法旨在提高相关矩阵特征向量的Krzanowski稳定性,经推算Sharifi等用相等的最大间距的正数特征值取代噪声特征值,并使新特征值和噪声特征值的和相等。上述去噪法的共同点是将小于λ+的特征值看作噪声,而λ+=1+H-1±2
为了量化特征向量的贡献,通常可采用局域理论中常用的反比参率,其定义如下:
| $ {I^k} = \sum\limits_{i = 1}^N {{{\left[{{V_{ik}}} \right]}^4}} $ |
其中, Vik(k=1, 2, …, N)是特征值λk的分量。两种极限情况:1)当Vk=(
| $ I_{{\rm{RMT}}}^k = N\int_{ - \infty }^\infty {\frac{{V_{ik}^4}}{{\sqrt {2\pi N} }}\exp \left( { - \frac{{V_{ik}^2}}{{2N}}} \right){\rm{d}}} {V_{ik}} = \frac{3}{N} $ |
有学者将蒙特卡罗模拟方法引入到小组合投资,研究发现文献[13-15]仅仅对λ+进行了评估,然而在小组合中,分析可知有必要对λ-同样进行模拟修正,以便获取股票网络最大限度的信息量。本文在文献[13]和文献[15]的基础上提出对λ+与λ-同时进行修正的蒙特卡罗模拟随机矩阵去噪法,且通过增加模拟次数获得更精确的近似值。
设相关系数矩阵CN的方差分别是δ12, δ22, …, δN2, 则CN对应的随机相关系数矩阵为R=AA′/L, 其中:
| $ \boldsymbol{A} = \left( {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1L}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2L}}}\\ \vdots & \vdots &{}& \vdots \\ {{x_{N1}}}&{{x_{N2}}}& \cdots &{{x_{NL}}} \end{array}} \right) $ |
其中, xij(i=1, 2, …, N, j=1, 2, …, L)是均值为0、方差为δi2的独立、正态分布的随机变量。因矩阵R是由A计算而得,故可对矩阵A根据概率统计进行模拟。下面将应用蒙特卡罗模拟法建立矩阵R的统计模拟模型并计算其最大特征值λ+、最小特征值λ-。具体流程如下:
步骤1 设定初始阈值ε0=0.0001, 由已知均值方差来构造随机矩阵A, 可在Matlab中实现。
步骤2 运用生成的随机矩阵A计算随机相关矩阵R及R的全部特征值并保留最大特征值λ+1和最小特征值λ-1。
步骤3 进行1000次的模拟,然后计算蒙特卡罗估计值λ+i(i=1, 2, …, 1000)和λ-i(i=1, 2, …, 1000), 遍历估计值并分别从中找到最大值和最小值,取这两个值作为模拟1000次时的蒙特卡罗模拟值。
步骤4 按公式ε=0.01*σ来计算蒙特卡罗估计值的误差。这里σ分别采用序列λ+i(i=1, 2, …, 1000)的标准差和λ-i(i=1, 2, …, 1000)的标准差来进行计算。
步骤5 取得满足条件的λ+和λ-。若ε≤ε0, 步骤3中获得的λ+或λ-就是对最大特征值或最小特征值的最终估计值;否则,继续进行步骤3,直至获得满足ε≤ε0的λ+和λ-, λ+和λ-就是对其的终极估计值。
3 实证分析 3.1 数据来源本文搜集了道琼斯中国88指数从2011年11月1日—2013年5月31日,以及香港恒生50指数从2014年1月1日—2015年6月1日的收盘价格数据。考虑到每只股票上市日期不同、停牌等各种原因,从中筛选出交易天数一致的股票,并对周末数据采用前一天的数据进行补缺,而对缺失数据连续超过7天的股票进行删除,最终分别选择88只股票和49只股票。
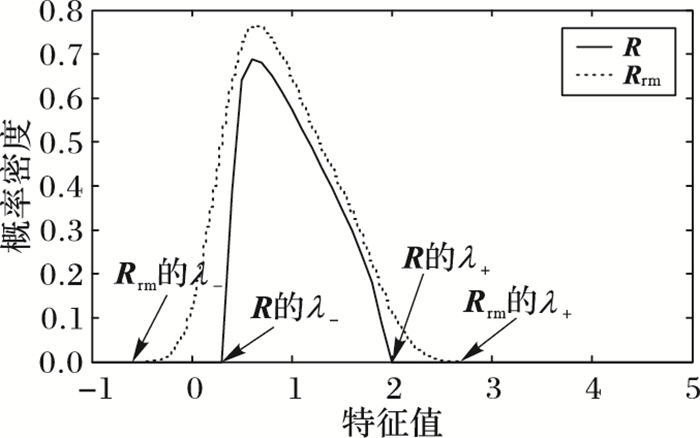
3.2 分析结果为说明可通过Matlab进行模拟随机矩阵,且模拟随机矩阵(Rrm)与RMT(R)在理论上存在某种程度的一致性,给出两个市场的RMT和模拟的特征值分布情况,如图 1所示。
|
图 1 道琼斯中国88的RMT和模拟随机矩阵的特征值分布 |
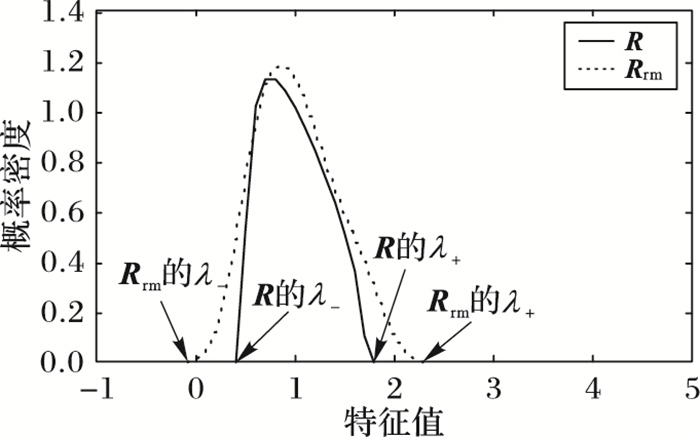
从理论上讲,模拟生成和随机矩阵理论是符合相同分布的随机矩阵,其特征值分布理应相同,不过从图 1和图 2可以看出,虽然在两个市场中R与Rrm的走势等基本吻合,但上下界都存在差异。这可能与R分布中λ-和λ+计算有关,因其计算的条件限制使得结果存在一定程度的失真。而基于蒙特卡罗模拟修正的RMT去噪法是通过大量数据模拟来生成随机矩阵,其大规模的数据模拟使得估计值更加精确。模拟结果如表 1所示。
|
图 2 香港恒生50的RMT和模拟随机矩阵的特征值分布 |
| 表 1 两个股票市场的6次模拟结果和随机矩阵理论特征值 |
观察表 1可以得知,道琼斯中国88指数的RMT的λ-=0.3719, λ+=1.9326, 其界定的噪声范围是[λ48, λ84]。利用蒙特卡罗模拟进行修正,本文选取上下界6次模拟的平均值分别是0.2609和2.0998,其界定的噪声范围是[λ36, λ84];香港恒生50指数的RMT的λ-=0.4791, λ+=1.7105, 其界定的噪声范围是[λ24, λ45], 对上下界模拟6次的取平均值分别是0.3556和1.9509,其界定的噪声范围是[λ18, λ46]。
由表 2可知:修正前两股市在上下界范围内的比例分别是42.0%和44.9%,而未落入上下界范围内的比例高达58%和55.06%,远超过噪声范围内的比例,与已有结论存在差异[16-17];而修正后落入最大最小范围内的比例分别是55.8%和59.1%,相对修正前的比例更加符合之前文献中的结论。同时还发现超出上界范围的比例变化不太明显。
| 表 2 修正前后特征值落在不同范围内的比值 |
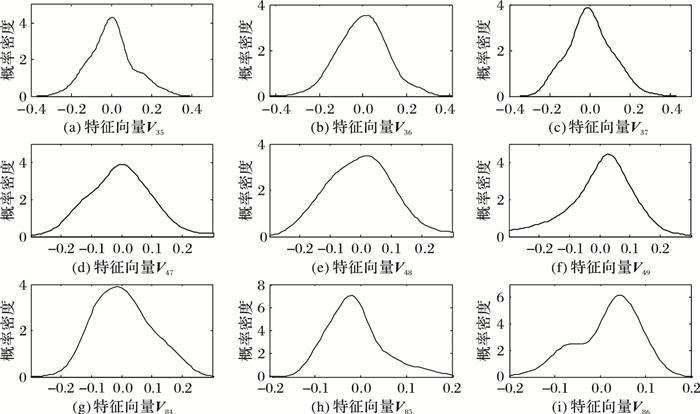
由修正过程可以看出,上界有微小的波动,而下界存在较大的差异,则下界之外的特征值可能存在有效信息。为此,对其所对应的特征向量的概率密度进行研究。由随机矩阵的构造原理可知其特征向量的分布基本符合标准正态分布,故在道琼斯中国88指数中选取了上界和下界中分别存在干扰的λ84, λ85, λ86和λ35, λ36, λ37, λ47, λ48, λ49的特征向量进行比较,香港恒生50则分别选择了λ17, λ18, λ24和λ45, λ46, λ47来进行对比。
从图 3可知,V35、V85和V86的分布出现明显的非对称性:V35在0.2附近出现异常;V85的均值小于0,图形存在向左偏移;V86则出现均值大于0图形右偏的情况。其余6个图形的分布基本上符合正态分布,基本满足对称和均值为0。从而V35、V85和V86是代表着股票市场中的有效信息,不应对其进行去噪处理,即去噪的特征值范围应为[λ36, λ84], 这与修正后界定的范围相一致。
|
图 3 道琼斯中国88的干扰噪声的特征向量的概率密度 |
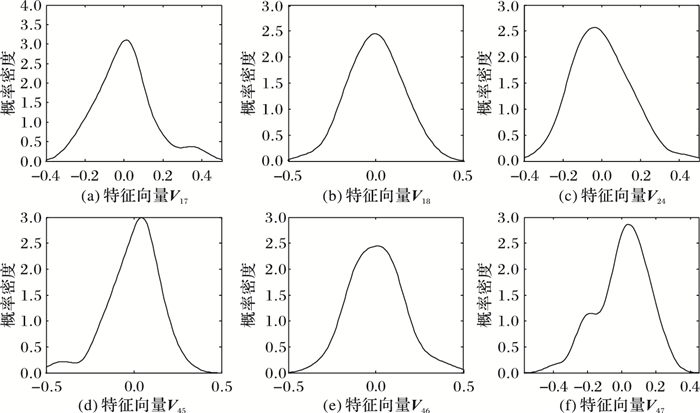
由图 4可清晰地看到V18和V46的分布几乎符合正态分布,V24和V45的分布也基本与正态分布相吻合,而V17和V47的分布则出现明显不对称性,即V17和V47可能代表股市的真实信息,不应对其去除噪声,以便尽可能地保留市场信息的完整性,故实际的噪声范围应为[λ18, λ46]。
|
图 4 香港恒生50指数干扰噪声附近的特征值分布 |
为考察结论的合理性,进一步研究反参比率的变化情况,从而确保去噪处理的有效性。结果如图 5、6所示。
|
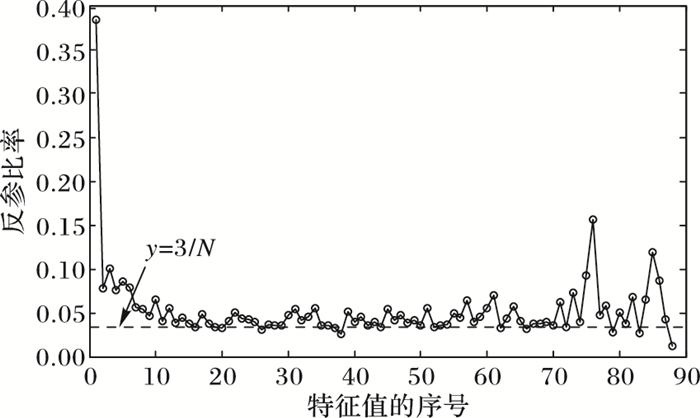
图 5 道琼斯中国88的反参比率分布 |
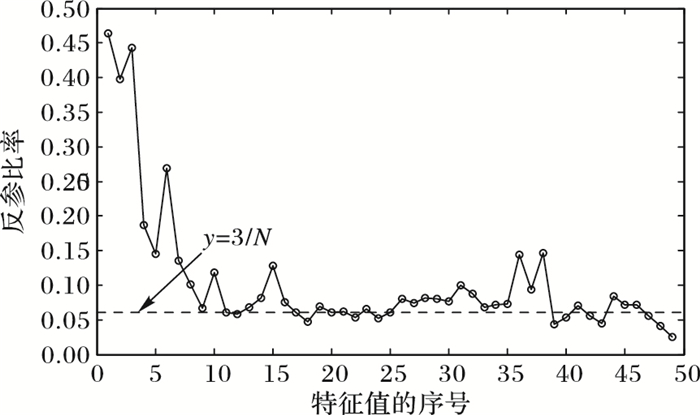
对比观察图 5与图 6可知,两股市中间部分特征值的反参比率在标准正态分布的反参比率值(y=3/N)的附近波动,而在噪声范围[λ36, λ84]和[λ18, λ46]的端点附近,信息特征值与噪声特征值的反参比率值相差甚微,这是由噪声信息和有效信息之间存在一定程度的排斥所致,从而模糊了有效信息与噪声间的差异,同时增强对整个市场进行去噪的干扰。
|
图 6 香港恒生50的反参比率分布 |
为衡量模拟修正法的去噪效果,选择对去噪后的相关矩阵进行投资组合,本文选择经典的马氏均值-方差模型。若投资者有N种可投资资产,Q=(Q1, Q2, …, QN)′表示期望收益率,Qi为第i种资产的期望收益率;N种资产收益率的协方差矩阵S=(δij)N×N;w=(w1, w2, …,wN)′是一个投资组合,wi表示资产在第i种证券上的投资比例,且有
| $ \begin{array}{l} \;\;\;\;\;\;\;\min \delta _p^2 = \boldsymbol{w}'\boldsymbol{Sw}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\left\{ \begin{array}{l} {\boldsymbol{R}_P} = \boldsymbol{w}'\boldsymbol{Q}\\ \boldsymbol{w}'{\boldsymbol{I}_N} = 1 \end{array} \right. \end{array} $ |
风险是判断投资组合优劣的一个重要的因素,在投资组合收益固定的情况下,方差(即风险)对应最优决策。故可将风险δp2作为Rp的函数,观察两者的变化趋势。经拉普拉斯变化及求解可知风险收益函数为:
| $ \delta _p^2 = \boldsymbol{w}'\boldsymbol{Sw} = \frac{{a\boldsymbol{R}_p^2 - 2b{\boldsymbol{R}_p} + c}}{\Delta } $ |
其中a=IN′S-1IN, b=IN′S-1Q, c=Q′S-1Q, Δ=ac-b2。两股市在不同去噪方法下的投资组合风险收益情况如图 7、8所示。
|
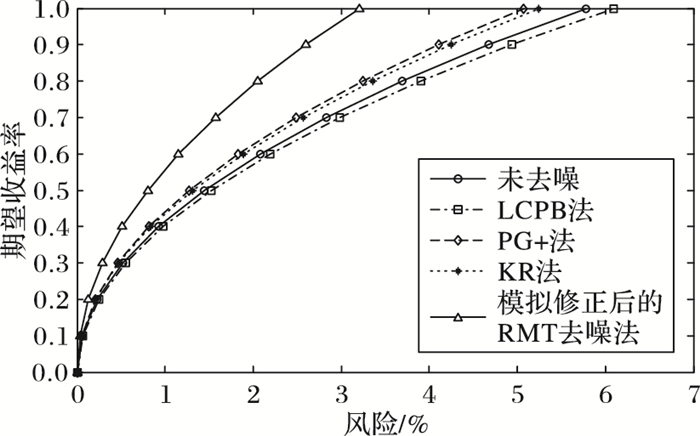
图 7 道琼斯中国88的风险收益曲线 |
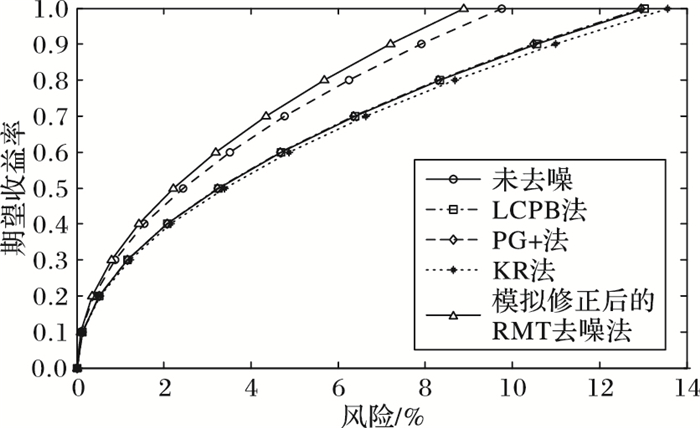
整体而言,随着期望收益率的增大,风险值也在不断上升。当固定期望收益率时,图 7和图 8都在模拟修正后的随机矩阵去噪法下的风险率最小。特别地,图 7未去噪与LCBP法、PG+法、KR法的风险收益基本相同,即这些方法并未达到去噪的目的;而图 8中未去噪比这三种去噪后的风险率更小,即对香港恒生50而言这三种方法去噪存在较大程度失真,严重毁坏了整个市场的有效性,从而使得去噪后的数据中包含的信息量太少,最终不能达到有效去噪的目的。这与市场包含的股票数目越多则其具有的信息量越丰富的实际相符,道琼斯中国88和香港恒生50分别具有88只股票和49只股票,即道琼斯中国88相对香港恒生50而言本身包含更多的信息,因此,当对这两个市场进行不合理的去噪时,包含信息量较少的香港恒生50就变得更加敏感,导致其出现未去噪的效果更优。然而,当对小组合的市场进行合理有效的去噪时,仍可最大化地去除其内部的干扰噪声,从而使得风险最小。
|
图 8 香港恒生50的风险收益曲线 |
本文提出了对小组合投资更加有效的蒙特卡罗模拟修正的RMT去噪法,即就资产数目较少的投资而言,小于λ-的特征值也包含着市场的有效信息,故可对代表噪声的随机矩阵进行大量的模拟平均,使得界定的噪声范围[λ-, λ+]更加精确,从而尽可能地保持市场信息的完整性与有效性。实证分析发现,在小组合投资中,模拟修正方法在投资组合方面的确更优于其他去噪法。在未来的研究中,我们计划利用复杂网络拓扑性质的一些指标来对提出的模拟方法进行更深一步的研究,使得研究结果更加全面,更加具有说服力。
| [1] |
罗英, 蔡玉梅, 崔小梅, 等. 资产组合协方差矩阵的信息结构[J].
预测, 2013, 32 (4) : 26-30.
( LUO Y, CAI Y M, CUI X M, et al. The information structure of the covariances between financial returns[J].
Forecasting, 2013, 32 (4) : 26-30.
) ( 0) 0)
|
| [2] |
李冰娜, 惠晓峰. 基于随机矩阵理论我国股票投资组合噪声分析及风险控制[J].
系统工程, 2012, 30 (8) : 38-44.
( LI B N, HUI X F. Study on noise analysis and risk control of portfolios from Chinese stock markets based on random matrix theory[J].
Journal of Systems Engineering, 2012, 30 (8) : 38-44.
) ( 0) 0)
|
| [3] |
KANG W, KIM K-K, SHIN H. Denoising Monte Carlo sensitivity estimates[J].
Operations Research Letters, 2012, 40 (3) : 195-202.
doi: 10.1016/j.orl.2012.01.006 ( 0) 0)
|
| [4] |
NILANTHA K G D R, RANASINGHE, MALMINI P K C. Eigenvalue density of cross-correlations in Sri Lankan financial market[J].
Physica A: Statistical Mechanics and its Applications, 2007, 378 (2) : 345-356.
doi: 10.1016/j.physa.2006.10.101 ( 0) 0)
|
| [5] |
LALOUX L, CIZEAU P, POTTERS M, et al. Random matrix theory and financial correlations[J].
International Journal of Theoretical and Applied Finance, 2000, 3 (3) : 391-397.
doi: 10.1142/S0219024900000255 ( 0) 0)
|
| [6] |
PLEROU V, GOPIKRISHNAN P, ROSENOW B, et al. A random matrix approach to cross-correlations in financial data [EB/OL]. [2015-12-14]. https://arxiv.org/pdf/cond-mat/0108023.pdf.
( 0) 0)
|
| [7] |
SHARIFI S, CRANE M, SHAMAIE A, et al. Random matrix theory for portfolio optimization: a stability approach[J].
Physica A: Statistical Mechanics and its Applications, 2004, 335 (3/4) : 629-643.
( 0) 0)
|
| [8] |
UTSUGI A, INO K, OSHIKAWA M. Random matrix theory analysis of cross correlations in financial markets[J].
Physical Review E, 2004, 70 (2) : 026110.
doi: 10.1103/PhysRevE.70.026110 ( 0) 0)
|
| [9] |
MALEVERGNE Y, SORNETTE D. Collective origin of the coexistence of apparent random matrix theory noise and of factors in large sample correlation matrices[J].
Physica A: Statistical Mechanics and its Applications, 2004, 331 (3/4) : 660-668.
( 0) 0)
|
| [10] |
KWAPIEĦ J, DROZDZ S, OSWIE P. The bulk of the stock market correlation matrix is not pure noise[J].
Physica A: Statistical Mechanics and its Applications, 2005, 359 (1) : 589-606.
( 0) 0)
|
| [11] |
DAI Y-H, XIE W-J, JIANG Z-Q, et al. Correlation structure and principal components in the global crude oil market [J/OL]. arXiv.org: arXiv:1405.5000. [2015-11-05]. http://de.arxiv.org/pdf/1405.5000.
( 0) 0)
|
| [12] |
高岳, 王家华, 杨爱军. 具有时变自由度的t-copula蒙特卡罗组合收益风险研究[J].
中国管理科学, 2011, 19 (2) : 10-15.
( GAO Y, WANG J H, YANG A J. Estimation on portfolio risk via time-varying t-copula and Monte-Carlo method[J].
Chinese Journal of Management Science, 2011, 19 (2) : 10-15.
) ( 0) 0)
|
| [13] |
POLITI M, SCALAS E, FULGER D, et al. Spectral densities of Wishart-Lévy free stable random matrices [EB/OL]. [2015-11-28]. http://discovery.ucl.ac.uk/1407446/1/0903.1629v1.pdf.
( 0) 0)
|
| [14] |
ZHANG M, RUBIO F, PALOMAR D P, et al. Finite-sample linear filter optimization in wireless communications and financial systems[J].
IEEE Transactions on Signal Processing, 2013, 61 (20) : 5014-5025.
doi: 10.1109/TSP.2013.2277835 ( 0) 0)
|
| [15] |
李冰娜.基于RMT去噪法股票投资组合风险优化研究[D].哈尔滨:哈尔滨工业大学, 2013:94-103.
( LI B N. Research on stock portfolio risk optimization based on the RMT denoising methods [D]. Harbin: Harbin Institute of Technology, 2013: 94-103.
) http://cdmd.cnki.com.cn/article/cdmd-10213-1013045110.htm ( 0) 0)
|
| [16] |
SENSOY A, YUKSEL S, ERTURK M. Analysis of cross-correlations between financial markets after the 2008 crisis[J].
Physica A: Statistical Mechanics and its Applications, 2013, 392 (20) : 5027-5045.
doi: 10.1016/j.physa.2013.06.046 ( 0) 0)
|
| [17] |
CONLON T, RUSKIN H J, CRANE M. Random matrix theory and fund of funds portfolio optimisation[J].
Physica A: Statistical Mechanics and its Applications, 2007, 382 (2) : 565-576.
doi: 10.1016/j.physa.2007.04.039 ( 0) 0)
|




