2. 东南大学 经济管理学院, 南京 211189 ;
3. 安徽大学 数学科学学院, 合肥 230601
2. School of Economics and Management, Southeast University, Nanjing Jiangsu 211189, China ;
3. School of Mathematical Science, Anhui University, Hefei Anhui 230601, China
WANG Cuicui, born in 1989, M.S., teaching assistant. Her research interests include type-2 fuzzy theory and its application.
YAO Dengbao, born in 1987, Ph.D. candidate. His research interests include financial engineering and risk management.
LI Baoping, born in 1976, M.S., associate professor. Her research interests include fuzzy decision-making.
随着互联网、大数据等新信息技术的发展和应用,数据信息日益呈现出模糊性、复杂性、犹豫性等不确定特征,传统数学工具已难以对其进行精确刻画。1965年Zadeh[1]提出模糊集理论,成为描述不确定问题的重要工具之一。随后,众多学者将模糊集理论不断拓展,逐渐建立了包含直觉模糊集[2]、区间直觉模糊集[3]和犹豫模糊集[4]等模糊系统理论。在模糊理论演变过程中最难理解的便是二型模糊理论[5],它将经典模糊集中的隶属度再次进行模糊化,整个隶属度函数由主、次隶属度联合表示,从而能够更加清晰和准确地刻画客观事物的不确定性本质。二型模糊理论在建立伊始并未得到学术界的普遍关注,直到近几年,该理论才开始不断地应用于故障诊断[6]、资源管理[7]、词计算[8]等领域。很多学者的研究不断丰富了二型模糊集的理论基础,如文献[9]通过构建二型模糊集的表示定理使得分析其不确定信息变得更加便捷,文献[10]给出了二型模糊集的一些集成算子,文献[11]对近年来二型模糊理论的发展进行了总结。
实际中,信息的不确定性常常代表风险、成本等负面因素,如何量化客观事物的不确定信息成为学术界研究的重要课题。为了测度模糊信息的不确定性,Zadeh[12]首次提出了模糊熵的概念,从此便成为了量化不确定信息的主要方法。为了拓广模糊熵的应用范围,该概念被引入到了模糊集的其他拓展理论中,如直觉模糊熵[13-15]、犹豫模糊熵[16-17]等。但是目前只有少部分学者开始研究二型模糊集的不确定测度问题,虽然文献[18-21]给出了一些构造二型模糊集的模糊熵公理,但都过分关注次隶属度的模糊性而忽略了主隶属度的模糊性和主、次隶属度之间的交叉影响,也未考虑主隶属度分布的分散性所产生的不确定信息。通过深入分析二型模糊集的内部结构发现,二型模糊信息的不确定性主要由两部分构成:模糊性和犹豫性,前者主要取决于主、次隶属度的模糊性,而后者基本上由主隶属度分布的分散程度所决定。因此,本文通过引入模糊因子和犹豫因子,克服了现有文献的不足,进一步完善了二型模糊熵的公理化准则,并根据距离测度与二型模糊熵的内在联系,给出了一些二型模糊熵的具体计算公式。
目前,大多数学者都以区间值二型模糊信息为数据环境,建立了一系列的多属性决策方法,如文献[22]针对机器人选择问题提出一类多属性决策方法,文献[23]将TOPSIS方法引入区间值二型模糊决策问题,文献[24]通过利用综合排序值方法解决区间值二型模糊信息的群决策问题。这些文献一方面缺乏对一般二型模糊信息的决策问题进行深入探讨,另一方面所建立的决策方法大多依赖于集成算子,没有考虑决策者的风险态度因素。文献[25]虽然讨论了二型模糊的决策方法,但其属性权重确定方法有些粗糙,且没有考虑决策者的风险态度问题。因此,本文针对属性权重信息完全未知的二型模糊信息决策问题,基于二型模糊熵构建非线性规划模型求解属性权重公式,并结合决策者的风险态度提出一类新的得分函数,从而建立一套系统完整的二型模糊多属性决策方法,并通过反舰导弹武器系统的方案选择问题验证了该决策方法的有效性和可行性。
1 基本概念定义1[5, 9] 二型模糊集。设X为一个有限论域,称集合:
| $ A = \left\{ {\left( {\left( {x,u} \right),{f_A}\left( {x,u} \right)} \right):u \in {J_x} \subset \left[{0,1} \right],{f_A}\left( {x,u} \right) \in \left[{0,1} \right],x \in X} \right\} $ |
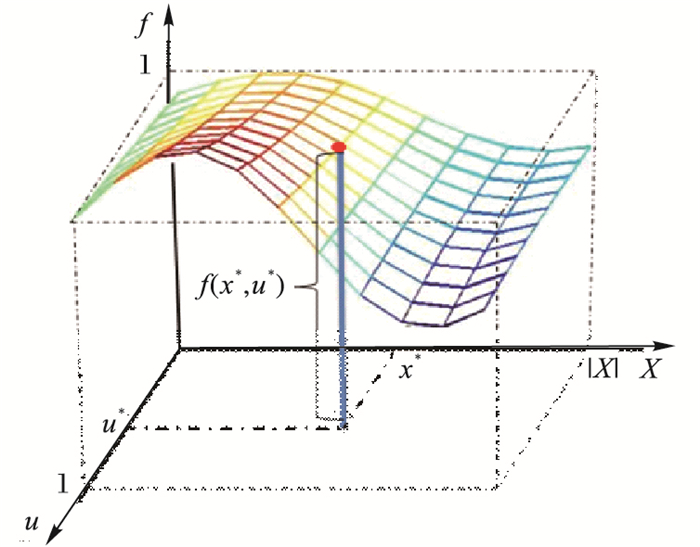
为论域X上的一个二型模糊集,其中u为主隶属度,fA(x, u)为次隶属度(如图 1所示)。
|
图 1 二型模糊隶属度函数的三维图 |
事实上,A还可以表示为
| $ A = \int_{x \in X} {\int_{u \in {J_x}} {{f_A}\left( {x,u} \right)/\left( {x,u} \right);{J_x} \subset \left[{0,1} \right]} } $ |
当论域X和Jx都是离散形式时,所有的“∫ ”全部替换为“∑”,也即:
| $ A = \sum\limits_{x \in X} {\frac{1}{x}\sum\limits_{u \in {J_x}} {\frac{{{f_A}\left( {u,x} \right)}}{u}} } $ |
为方便起见,记T2FS(X)为论域X上所有二型模糊集的全体,P(X)为X上所有经典集合的全体。根据文献[20]的规定,记AC为A的补集,其中fAC(x, u)=fA(x, 1-u)。
定义2[22] 设A∈T2FS(X),则A在论域上的任意一点与该点的主隶属度之间笛卡尔积之并为一个平面区域,称该区域为A的不确定覆盖域(Footprint Of Uncertainty, FOU),记为FOU(A)=$\bigcup\limits_{\forall x \in X} {{J_x}} $。
2 二型模糊熵自从模糊集理论提出以后,对其不确定信息的度量成为理论界研究的基础性问题之一,为此,Zadah将信息论中的“熵”的概念引入模糊集中,作为度量其模糊性的一种重要工具。随后,模糊熵又被推广到直觉模糊集和犹豫模糊集等理论中,用以量化其不确定信息。文献[18-20]在二型模糊集中引入了二型模糊熵,但他们只考虑了次隶属度的模糊性而忽略了主隶属度的模糊性,同时也没有考虑因主隶属度的分散性所引发的不确定性。为了克服这些不足,需要重新分析二型模糊集中产生不确定性信息的内在因素,由此提出一个构造二型模糊熵的公理化准则。
2.1 不确定性因子只有深刻理解二型模糊集的不确定性才能建立一个合理有效的二型模糊熵。通过分析发现二型模糊集的不确定性主要由其模糊性和犹豫性两方面组成,其中模糊性又可以分为主隶属度的模糊性和次隶属度的模糊性,主隶属度的模糊性可以用主隶属度与1/2的加权平均接近程度来测度,而次隶属度的模糊性则可以用次隶属度与1/2的算术平均接近程度来描述;二型模糊集的犹豫性主要体现在主隶属度的分散性方面,可以用其平均离散程度来刻画。为了量化二型模糊集的模糊性和犹豫性,这里参考文献[15]的方法,引入模糊因子和犹豫因子。
不失一般性,这里先考虑单元素论域,即X={x}。对任意的A∈T2FS(X),不妨记ΔA(x)和σA(x)分别为A的模糊因子和犹豫因子,并分别用来刻画A的模糊性和犹豫性的强弱。ΔA(x)和σA(x)可按照以下公式计算:
| $\Delta A\left( x \right) = \sqrt {\left( {{{\left( {\Delta _A^u\left( x \right)} \right)}^2} + {{\left( {\Delta _A^f\left( x \right)} \right)}^2}} \right)/2} $ | (1) |
其中:$\Delta _A^u\left(x \right)=\int_{{J_x}} {\left| {u-\frac{1}{2}} \right|{w_x}\left(u \right){\text{d}}u}, \Delta _A^f\left(x \right)=\frac{1}{{\left| {{J_x}} \right|}}\int_{{J_x}} {\left| {f\left({x, u} \right)-\frac{1}{2}} \right|{\text{d}}u} $分别为反映主、次隶属度模糊性强弱的测度;${w_x}\left(u \right)=\frac{{f\left({x, u} \right)}}{{\int_{{J_x}} {f\left({x, u} \right){\text{d}}u} }}$为相对权重,反映了次隶属度对主隶属度的直接影响。
| ${\sigma _A}\left( x \right) = \int_{{J_x}} {\left| {u - \bar u} \right|{w_x}\left( u \right){\text{d}}u} $ | (2) |
其中:$\bar u=\int_{{J_x}} {u{w_x}\left(u \right){\text{d}}u} $为主隶属度的加权平均。
很容易可以验证$\Delta _A^u\left(x \right), \Delta _A^f\left(x \right) \in \left[{0, 1/2} \right] \Rightarrow \Delta A\left(x \right)\left[{0, 1/2} \right]$和σA(x)∈[0, 1/2],因此有0≤ΔA(x)+σA(x)≤1。另外,不难得出ΔA(x)=ΔAC(x)和σA(x)=σAC(x)。值得注意的是二型模糊集A的模糊性随着模糊因子ΔA(x)的减小而增强,其犹豫性随着犹豫因子σA(x)的增大而增强。换句话来说,A的不确定性可以由二元组(ΔA, σA)完全决定,因此后面所构建的二型模糊熵也都以这个二元组为基础。
2.2 二型模糊熵的公理化准则鉴于文献[18-21]研究中的不足,这里重新完善二型模糊熵的公理化准则。
定义3 设E(A)=g(ΔA, σA):T2FS(X)→[0,1]为一个映射,若E(A)满足以下准则:
1)E(A)=0当且仅当A∈P(X);
2)E(A)≤1, $∀$A∈T2FS(X);
3)E(A)=E(AC);
4)g(ΔA, σA)是一个随着ΔA增大而递减,随σA增大而递增的连续函数, 则称E(A)为A的二型模糊熵。
可以看出,定义3中的准则(1)和(3)与文献[18-21]相同,但这里没有给出E(A)的正则化条件,即E(A)何时能够取到其最大值1。这主要是由于模糊因子ΔA和犹豫因子σA的最大值点并不一致,而ΔA和σA又具有互补性,因此,只需要将E(A)控制在[0,1]即可,这样设定也更具灵活性。同时,文献[18-21]只指出“当A比B更具确定性(crisper)时才有E(A)≤E(B)”,但没有对这种“确定性”作更清晰的量化,而准则(4)已经明确说明了E(A)的变化趋势。因此,本文所构建的二型模糊熵公理化准则应该更具灵活性、合理性和准确性。
2.3 基于距离的二型模糊熵公式鉴于二型模糊集A的不确定性可由(ΔA, σA)来完全且唯一刻画,如果记一个理想集I*具有最强的不确定性,即(ΔI*, σI*)=(0, 1/2),类似于文献[15],当A越靠近I*时所对应的E(A)越大,反之亦然。这样便可以利用距离测度来构建如下的二型模糊熵公式:
| $E\left( A \right) = \varphi \left( {D\left( {A,{I^ * }} \right)} \right)$ | (3) |
其中:D(A, I*)为A和I*之间的标准化距离;φ(·)为[0,1]→[0,1]上的实值连续函数,如φ(y)=1-y,cos(πy)/2等。下面主要以φ(y)=1-y为例进行分析。
根据式(3)结合不同的距离公式,可以得到如下的二型模糊熵公式:
1) 欧氏距离:
| $\begin{gathered} E\left( A \right) = 1 - {D_E}\left( {A,{I^ * }} \right) = \hfill \\ 1 - \sqrt {\frac{{\Delta _A^2\left( x \right) + {{\left( {{\sigma _A}\left( x \right) - \frac{1}{2}} \right)}^2}}}{2}} \hfill \\ \end{gathered} $ | (4) |
2) 海明距离:
| $\begin{gathered} E\left( A \right) = 1 - {D_E}\left( {A,{I^ * }} \right) = \hfill \\ 1 - \frac{{\left| {{\Delta _A}\left( x \right) - 0} \right| + \left| {{\sigma _A}\left( x \right) - \frac{1}{2}} \right|}}{2} = \hfill \\ \frac{3}{4} + \frac{1}{2}\left( {{\sigma _A}\left( x \right) - {\Delta _A}\left( x \right)} \right) \hfill \\ \end{gathered} $ | (5) |
3) 广义距离:
| $\begin{gathered} E\left( A \right) = 1 - {D_G}\left( {A,{I^ * }} \right) = \hfill \\ 1 - {\left\{ {\frac{{\Delta _A^\lambda \left( x \right) + {{\left| {{\sigma _A}\left( x \right) - 1/2} \right|}^\lambda }}}{2}} \right\}^{\frac{1}{\lambda }}};\lambda {\text{ > }}0 \hfill \\ \end{gathered} $ | (6) |
不难证明式(4)~(6)满足定义3的四条准则,还可以将其推广到多元素有限论域X={x1, x2, …, xm},式(4)~(6)可转化为:
| $E\left( A \right) = 1 - \frac{1}{m}\sum\limits_{i = 1}^m {\sqrt {\frac{{\Delta _A^2\left( {{x_i}} \right) + {{\left( {{\sigma _A}\left( x \right) - \frac{1}{2}} \right)}^2}}}{2}} } $ | (7) |
| $E\left( A \right) = \frac{3}{4} + \frac{1}{{2m}}\sum\limits_{i = 1}^m {\left( {{\sigma _A}\left( {{x_i}} \right) - \Delta A\left( {{x_i}} \right)} \right)} $ | (8) |
| $\begin{gathered} E\left( A \right) = 1 - \frac{1}{m}\sum\limits_{i = 1}^m {{{\left\{ {\frac{{\Delta _A^\lambda \left( {{x_i}} \right) + {{\left| {{\sigma _A}\left( {{x_i}} \right) - 1/2} \right|}^\lambda }}}{2}} \right\}}^{\frac{1}{\lambda }}}} \hfill \\ \lambda {\text{ > }}0 \hfill \\ \end{gathered} $ | (9) |
对于一个以二型模糊信息为数据环境的多属性决策问题,各属性对于决策者来说并非同等重要,需要通过属性权重加以区别。但在实际决策过程中,决策者由于知识结构和决策经验的不足,往往不能充分掌握各决策属性的真实信息,所以这里给出一种基于二型模糊熵的属性权重确定方法。假设有m个对象(x1, x2, …, xm)和n个决策属性(a1, a2, …, an),对应的属性权重为ω={ω1, ω2, …, ωn}且满足$\sum\limits_{j=1}^n {{\omega _j}} $=1, ωj∈[0,1], 1≤j≤n。假设所有的属性值都用二型模糊集的形式进行描述,记原始数据矩阵为R=(rij)m×n,其中:rij$\hat=${(uijk, fijk):1≤k≤nij},uijk和fijk分别为对象xi在属性aj下的第k个主、次隶属度,nij为rij中包含主隶属度的数量。
3.1 决策方法下面给出基于二型模糊信息环境的多属性决策方法:
步骤1 根据不同属性类型对原始数据进行标准化处理。假设标准化后的决策矩阵为D=(dij)m×n,其中:
| ${d_{ij}} = \left\{ \begin{gathered} \left\{ {\left( {u_{ij}^k,f_{ij}^k} \right):1 \leqslant k \leqslant {n_{ij}}} \right\},\;\;\;\;\;\;\;{a_j}是效益型 \hfill \\ \left\{ {\left( {1 - u_{ij}^k,f_{ij}^k} \right):1 \leqslant k \leqslant {n_{ij}}} \right\}\;\;\;\;{a_j}是成本型 \hfill \\ \end{gathered} \right.$ | (10) |
步骤2 将标准化后的决策D转化为得分矩阵S=(sij)m×n,其中:
| ${s_{ij}} = {\bar u_{ij}} + \theta {v_{ij}}$ | (11) |
其中:${\bar u_{ij}}=\sum\limits_{k=1}^{{n_{ij}}} {u_{ij}^kw_{ij}^k{v_{ij}}=} \sum\limits_{k=1}^{{n_{ij}}} {\left| {u_{ij}^k-{{\bar u}_{ij}}} \right|w_{ij}^k} $分别为dij主隶属度的加权平均值和加权平均离差。θ为决策者的风险态度系数,当θ>0说明决策者是风险偏好型,且θ值越大反映了决策者风险偏好程度越高;当θ=0说明决策者是风险中性的;当θ < 0时说明决策者是风险厌恶型,θ值越小反映了决策者风险厌恶程度越高。
步骤3 为了减少决策的误差和风险,决策者一般会希望决策过程尽可能地依赖于确定信息,因此,各属性的权重设定应该尽可能减少不确定信息对决策结果的影响。基于这思想可以建立如下非线性规划模型:
| $\begin{gathered} \min F\left( \omega \right) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {E\left( {{d_{ij}}} \right)\omega _j^2} } \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\sum\limits_{j = 1}^n {{\omega _j} = 1,{\omega _j} \in \left[{0,1} \right],1 \leqslant j \leqslant n} \hfill \\ \end{gathered} $ | (12) |
利用Lagrange乘数法,可以求得各属性的权重公式为:
| ${\omega _j} = {\left[{\sum\limits_{j = 1}^n {{{\left( {\sum\limits_{i = 1}^m {E\left( {{d_{ij}}} \right)} } \right)}^{ - 1}}} } \right]^{ - 1}}{\left( {\sum\limits_{i = 1}^m {E\left( {{d_{ij}}} \right)} } \right)^{ - 1}}$ | (13) |
步骤4 根据公式Score=SωT计算每个对象的总体得分,并按照该得分对所有对象进行排序,从而得到最优对象。
3.2 实例分析某制造商正在研制某种反舰导弹武器系统,现有5个备选方案(x1, x2, …, x5)可供制造商选择,而评价反舰导弹武器系统的性能指标(属性)主要有4个:导弹命中与毁伤能力(a1)、电磁抗干扰能力(a2)、导弹制导与飞行控制能力(a3)、载舰机动能力(a4)。制造商聘请专家根据这些指标对所有备选方案进行评估,并将评估数据用二型模糊集的形式给出。由于上述4个属性都是效益型指标,因此,原始数据矩阵就是标准化后的决策矩阵(如表 1所示)。
| 表 1 二型模糊决策矩阵 |
下面根据上述多属性决策方法确定最优方案。
1) 根据决策者不同的风险态度设置参数θ,这里分别将参数θ设置为1、0和-1三种,结合式(11)计算所有方案在不同风险偏好下的得分矩阵Sθ如下:
| $ \begin{gathered} {S_{\theta {\text{ = }}1}}{\text{ = }}\left[{\begin{array}{*{20}{c}} {0.4694}&{0.4628}&{0.5173}&{0.6118} \\ {0.4742}&{0.6087}&{0.6094}&{0.6116} \\ {0.4918}&{0.6331}&{0.5143}&{0.6089} \\ {0.4438}&{0.6710}&{0.5224}&{0.5918} \\ {0.4953}&{0.5167}&{0.5587}&{0.6080} \end{array}} \right] \hfill \\ {S_{\theta {\text{ = 0}}}}{\text{ = }}\left[{\begin{array}{*{20}{c}} {0.3714}&{0.3273}&{0.4556}&{0.5692} \\ {0.3579}&{0.4000}&{0.5250}&{0.5682} \\ {0.3625}&{0.4190}&{0.4500}&{0.5615} \\ {0.3625}&{0.4389}&{0.4714}&{0.5429} \\ {0.3688}&{0.3333}&{0.5091}&{0.5600} \end{array}} \right] \hfill \\ {S_{\theta {\text{ = - 1}}}}{\text{ = }}\left[{\begin{array}{*{20}{c}} {0.2735}&{0.1917}&{0.3938}&{0.5266} \\ {0.2416}&{0.1913}&{0.4406}&{0.5248} \\ {0.2796}&{0.2050}&{0.3857}&{0.5142} \\ {0.2813}&{0.2068}&{0.4204}&{0.4939} \\ {0.2422}&{0.1500}&{0.4595}&{0.5120} \end{array}} \right] \hfill \\ \end{gathered} $ |
2) 根据式(13),结合式(4)~(6),分别计算所有属性的权重,这里取λ=1.5,如表 2所示。
| 表 2 不同熵公式下的属性权重 |
3) 利用Score=SθωT可得到所有方案的总得分,如表 3所示。
由表 3可以看出,一方面,对于同种风险态度的决策者来说,采用不同的二型模糊熵公式并不影响最终的决策结果,说明这些公式具有内在的一致性;另一方面,对于风险偏好型和风险中性的决策者来说,虽然选取的最优方案都是x2,但方案x3和x4的排序正好颠倒,而对于风险厌恶型的决策者,选取的最优方案变为x4,且其他方案的排序与前两种类型有较大的不同,可见决策者的风险态度对最终决策结果确实会产生较大影响,这也反映了将风险态度引入决策模型是完全合理的。
| 表 3 所有方案的总得分及排序 |
通过与文献[25]对比发现,上述决策方法主要具有两个优点:第一,属性权重的确定方法更加客观和精细,更符合具体问题具体分析的原则;第二,文献[26]的得分函数只是上述风险态度参数θ=0的情形,实际上本文决策方法考虑了决策者的风险态度,决策过程更具灵活性。虽然文献[22-24]的决策方法不适用于一般形式的二型模糊信息环境,但从决策思想上来说,上述决策方法突破了这些文献利用集成算子进行信息融合的分析框架,而是通过得分函数将复杂的二型模糊信息转换为简单的单值实数信息,从而避免了集成算子的不同选取对决策结果的影响。
4 结语本文将二型模糊信息的不确定性分解为模糊性和犹豫性两类,通过引入模糊因子和犹豫因子构建二型模糊熵的公理化准则,并结合熵测度与距离测度之间的内在联系,给出了三类二型模糊熵的计算公式。为了减少各属性不确定信息对决策结果的不利影响,针对属性权重信息完全未知的情形,利用二型模糊熵建立非线性规划模型,从而确定属性权重的计算公式。考虑到决策者的风险态度会对决策结果产生影响,通过设置不同的风险态度参数值将其区分为风险偏好型、风险中性和风险厌恶型三类,并提出了一类新的得分函数。最后,通过将所构建的二型模糊多属性决策方法应用于反舰导弹武器系统的方案选择问题中,从而验证了该决策方法的可行性,并与现有文献进行了对比分析以体现其灵活性。
| [1] |
ZADEH L A. Fuzzy sets[J].
Information and Control, 1965, 8 (3) : 338-353.
doi: 10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [2] |
ATANASSOV K T. Intuitionistic fuzzy sets[J].
Fuzzy Sets and Systems, 1986, 20 (1) : 87-96.
doi: 10.1016/S0165-0114(86)80034-3 ( 0) 0)
|
| [3] |
ATANASSOV K, GARGOV G. Interval valued intuitionistic fuzzy sets[J].
Fuzzy Sets and Systems, 1989, 31 (3) : 343-349.
doi: 10.1016/0165-0114(89)90205-4 ( 0) 0)
|
| [4] |
TORRA T. Hesitant fuzzy sets[J].
International Journal of Intelligent Systems, 2010, 25 (6) : 529-539.
( 0) 0)
|
| [5] |
ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning[J].
Information Sciences, 1975, 8 (3) : 199-249.
doi: 10.1016/0020-0255(75)90036-5 ( 0) 0)
|
| [6] |
AGVERO J R, VARGAS A. Calculating functions of interval type-2 fuzzy numbers for fault current analysis[J].
IEEE Transactions on Fuzzy Systems, 2007, 15 (1) : 31-40.
doi: 10.1109/TFUZZ.2006.889757 ( 0) 0)
|
| [7] |
GILAN S S, SEBT M H, SHAHHOSSEINI V. Computing with words for hierarchical competency based selection of personnel in construction companies[J].
Applied Soft Computing, 2012, 12 (2) : 860-871.
doi: 10.1016/j.asoc.2011.10.004 ( 0) 0)
|
| [8] |
MENDEL J M. Computing with words and its relationship with fuzzistics[J].
Information Sciences, 2007, 177 (4) : 988-1006.
doi: 10.1016/j.ins.2006.06.008 ( 0) 0)
|
| [9] |
MENDEL J M, JOHN R I B. Type-2 fuzzy sets made simple[J].
IEEE Transactions on Fuzzy Systems, 2002, 10 (2) : 117-127.
doi: 10.1109/91.995115 ( 0) 0)
|
| [10] |
KARNIK N N, MENDEL J M. Operations on type-2 fuzzy sets[J].
Fuzzy Sets and Systems, 2001, 122 (2) : 327-348.
doi: 10.1016/S0165-0114(00)00079-8 ( 0) 0)
|
| [11] |
MENDEL J M. Advances in type-2 fuzzy sets and systems[J].
Information Sciences, 2007, 177 (1) : 84-110.
doi: 10.1016/j.ins.2006.05.003 ( 0) 0)
|
| [12] |
ZADEH L A. Probability measures of fuzzy events[J].
Journal of Mathematical Analysis and Applications, 1968, 23 (2) : 421-427.
doi: 10.1016/0022-247X(68)90078-4 ( 0) 0)
|
| [13] |
SZMIDT E, KACPRZYK J. Entropy for intuitionistic fuzzy sets[J].
Fuzzy Sets and Systems, 2001, 118 (3) : 467-477.
doi: 10.1016/S0165-0114(98)00402-3 ( 0) 0)
|
| [14] |
HUNG W L, YANG M S. Fuzzy entropy on intuitionistic fuzzy sets[J].
International Journal of Intelligent Systems, 2006, 21 (4) : 443-451.
doi: 10.1002/(ISSN)1098-111X ( 0) 0)
|
| [15] |
MAO J, YAO D, WANG C. A novel cross-entropy and entropy measures of IFSs and their applications[J].
Knowledge-Based Systems, 2013, 48 (2) : 37-45.
( 0) 0)
|
| [16] |
XU Z, XIA M. Hesitant fuzzy entropy and cross-entropy and their use in multiattribute decision-making[J].
International Journal of Intelligent Systems, 2012, 27 (9) : 799-822.
doi: 10.1002/int.v27.9 ( 0) 0)
|
| [17] |
ZHAO N, XU Z, LIU F. Uncertainty measures for hesitant fuzzy information[J].
International Journal of Intelligent Systems, 2015, 30 (7) : 818-836.
doi: 10.1002/int.2015.30.issue-7 ( 0) 0)
|
| [18] |
HWANG C M, YANG M S, HUNG W L, et al. Similarity, inclusion and entropy measures between type-2 fuzzy sets based on the Sugeno integral[J].
Mathematical and Computer Modelling, 2011, 53 (9/10) : 1788-1797.
( 0) 0)
|
| [19] |
HWANG C M, YANG M S, HUNG W L. On similarity, inclusion measure and entropy between type-2 fuzzy sets[J].
International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2012, 20 (3) : 433-449.
doi: 10.1142/S0218488512500225 ( 0) 0)
|
| [20] |
TAKÁC Z. Inclusion and subsethood measure for interval-valued fuzzy sets and for continuous type-2 fuzzy sets[J].
Fuzzy Sets and Systems, 2013, 224 (4) : 106-120.
( 0) 0)
|
| [21] |
邓廷权, 王占江, 王培培, 等. 二型模糊集的模糊熵研究[J].
控制与决策, 2012, 27 (3) : 408-412.
( DENG T Q, WANG Z J, WANG P P, et al. Study on fuzzy entropy of type-2 fuzzy sets[J].
Control and Decision, 2012, 27 (3) : 408-412.
) ( 0) 0)
|
| [22] |
GHORABAEE M K. Developing an MCDM method for robot selection with interval type-2 fuzzy sets[J].
Robotics and Computer-Integrated Manufacturing, 2016, 37 (C) : 221-232.
( 0) 0)
|
| [23] |
CHEN T Y. An interval type-2 fuzzy technique for order preference by similarity to ideal solutions using a likelihood-based comparison approach for multiple criteria decision analysis[J].
Computers and Industrial Engineering, 2015, 85 (C) : 57-72.
( 0) 0)
|
| [24] |
QIN J D, LIU X W. Multi-attribute group decision making using combined ranking value under interval type-2 fuzzy environment[J].
Information Sciences, 2015, 297 (C) : 293-315.
( 0) 0)
|
| [25] |
YAO D, LIU X, ZHANG X, et al. Type-2 fuzzy cross-entropy and entropy measures and their applications[J].
Journal of Intelligent and Fuzzy Systems, 2016, 30 (4) : 2169-2180.
doi: 10.3233/IFS-151986 ( 0) 0)
|




