2. 中国矿业大学 信息与电气工程学院, 江苏 徐州 221008
2. School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou Jiangsu 221008, China
XIE Hongxia, born in 1980, Ph. D., associate professor. Her research interests include coal power equipment fault diagnosis and maintenance, data mining.
MA Xiaowei, born in 1992, M. S. candidate. His research interests include electrical equipment fault diagnosis, particle swarm optimization.
CHEN Xiaoxiao, born in 1992, M. S. candidate. Her research interests include electrical equipment fault diagnosis.
XING Qiang, born in 1990, M. S. candidate. His research interests include power quality detection.
在现实生活中很多实际问题都可以抽象为数值函数寻优问题,有一些问题如神经网络集成、组合投资等,不仅要在解空间中找出全局最优解,还要尽可能多地找出有意义的局部最优解,为问题的解决提供足够的信息,此类问题被称为多模态优化问题[1-2],抽象出的函数为多模态函数(multi-modal function),而解决此类问题的过程便是多模态函数的寻优。
粒子群算法(Particle Swarm Optimization, PSO)[3]是Kennedy与Eberhard观察模仿鸟类迁徙觅食的群体行为,于1995年提出的一种群体智能优化技术。标准的PSO是单极值搜索的算法,一次只能搜索到一个极值点,对多模态问题并不适用。小生境(niche)技术[4]是一种仿生技术,将自然界中种群的概念与群体智能算法相结合,通过一定的方法,将整个种群划分为许多个独立的子种群,每个子种群可以独立地进化。近几年,将小生境技术与群体智能算法相结合,提出了一些适用于多模态优化问题的寻优方法。将小生境技术与遗传算法(Genetic Algorithm, GA)相结合提出了小生境遗传算法(Niche Genetic Algorithm, NGA)[5]与种群保护遗传算法(Species Conserving Genetic Algorithm, SCGA)[6]等多模态优化算法,但这些基于遗传算法的多模态优化方法大多存在计算开销大、收敛速度慢、局部搜索精度低的缺陷[7]。将小生境技术与粒子群相结合,文献[8]提出了基于种群的粒子群算法(Species-based PSO, SPSO),将粒子群划分为数个种群各自独立进化,种群的数目在进化过程中不断变化,但是在极值点分布较分散的情况下有可能会漏掉某些较优的解;并且SPSO在每一代的粒子中生成种群种子,这使得粒子在收敛过程中抖动,导致算法稳定性降低。文献[9]提出了一种基于k-均值聚类算法的粒子群算法(k-means-based PSO, kPSO),使用贝叶斯信息规则和标准k-均值聚类算法自动识别聚类数目;但是该算法需要预先设置参数c与集群之间的步数,降低了该算法的实用价值。文献[10]提出了多分组粒子群算法(Multi-Grouped PSO, MGPSO),为搜索到的每一个极值分配一个随进化代数增加不断减小的区域来避免最优解重叠;但是如果在种群没有足够收敛之前极值范围变得太小, 那么很可能会导致某些种群找不到极值点。
为了提高多模态粒子群算法的搜索性能,在SPSO的基础上提出了一种基于多种群的改进粒子群算法(Enhanced Multi-Species-based Particle Swarm Optimization, EMSPSO)。该算法一方面改进了种群生成策略,通过在个体最优值中选择种群种子,减少了粒子在搜索过程中的抖动,使得算法更加稳定;另一方面引入了冗余粒子重新初始化策略,提高了粒子的利用率,增强了算法的全局搜索能力;此外对速度更新公式进行了改进,使算法在收敛速度与全局搜索能力之间取得平衡。
1 粒子群算法基本理论在标准粒子群算法中,假设目标问题对应一个D维的解空间,被初始化随机分布到此解空间中的n个粒子组成粒子群G=(X1, X2, …, Xn),第i个粒子在解空间中的位置可以用一个D维向量Xi=(xi1, xi2, …, xiD)T来表示,其中xi1, xi2, …, xiD是在D维解空间中的坐标,每一个粒子的位置都对应着目标问题的一个解。将由目标问题抽象得来的目标函数作为适应度函数,可计算出每一粒子所对应的适应度值,适应度值体现了解的优劣。每个粒子除了位置还具有速度属性,第i个粒子的速度可以表示为向量Vi=(vi1, vi2, …, viD)T。在迭代寻优的过程中,使用向量pbest记录粒子群的个体最优值,向量gbest记录全局最优值。
PSO的寻优过程是一个循环进化的过程,在每一次循环的过程中,每个粒子都会根据式(1)、(2)来更新自己的速度与位置,在达到终止条件后停止迭代循环。
| $\begin{gathered} V_i^{k + 1} = \omega V_i^k + {c_1}{r_1}\left( {pbest_i^k - X_i^k} \right) + \hfill \\ {c_2}{r_2}\left( {pbes{t^k} - X_i^k} \right) \hfill \\ \end{gathered} $ | (1) |
| $X_i^{k + 1} = X_i^k + V_i^{k + 1}$ | (2) |
其中:i=1, 2, …, n;k为当前进化代数;r1与r2是均匀分布在[0,1]的随机数,以维持群体的多样性;c1与c2为加速度因子,分别标志着粒子趋向于个体最优值与全局最优值的趋势大小;ω为惯性权重,其主要目的是更好地平衡PSO的全局探测与局部搜索能力。研究表明,当ω设置较大时,则有利于全局整体搜索;反之,则有利于局部深度挖掘。
为了保持PSO性能的稳定,Clerc等[11]提出采用收缩因子来保证算法收敛,这种形式的PSO采用式(3)所示的更新公式:
| $V_i^{k + 1} = \chi \left( {V_i^k + {c_1}{r_1}\left( {pbest_i^k - X_i^k} \right) + {c_2}{r_2}\left( {pbes{t^k} - X_i^k} \right)} \right)$ | (3) |
其中,收缩因子χ的取值为:
| $\chi = 2/|2 - \varphi - \sqrt {{\varphi ^2} - 4\varphi } $ | (4) |
参数需满足φ=c1+c2,φ>4。
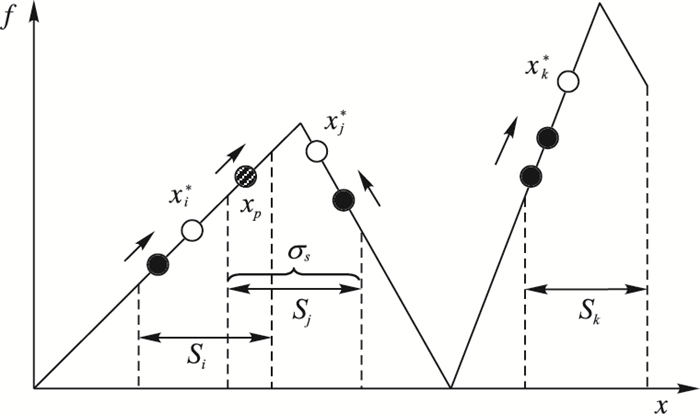
2 基于多种群的改进粒子群算法在EMSPSO中,种群是位置相对集中且具有相近进化行为的一组粒子,种群具有两个关键的概念:种群种子x*与种群距离σS。种群种子是种群中适应度最优的粒子,每一个种群只有一个种群种子,每一个种群种子都对应了搜索到的一个极值点;而种群距离决定了种群范围的大小。
EMSPSO使用欧氏距离[12]来度量粒子间距离,每一次迭代更新,都要在个体最优值pbest中选择出本代的种群种子,再根据种群种子将整个粒子群划分为若干个种群。每一个种群都有自己的范围,若xi*为种群Si的种子,则Si的范围便是以xi*为中心,半径为σS的区域。
P=(pbest1, pbest2,…,pbestn)是所有粒子pbest的集合,选择种群种子的基本思想是:将P中的所有元素,即所有粒子的pbest按适应度值从优到劣排序,首先将第一个元素(也是适应度值最优的pbest)标记为种子,然后判断第二个元素是否处于某一个种子的种群范围内,若没有则把第二个粒子也标记为种子。接着判断第三个元素,依此类推,直到遍历P中所有元素。最后,将所有找到的种群种子形成集合XS。
若一个粒子处于某一个种群的范围内,则这个粒子便属于此种群;若有粒子不处于任何一个种群的范围之内,则将其划分到最近的种群中;若一个粒子同时处于两个种群的范围内,优先选择种群种子适应度较优的种群。如图 1所示,粒子xP同时位于种群Si与Sj的范围内且f(xj*)f(xi*),所以xP属于种群Sj。通过这样的规则,可以将整个粒子群分为若干个种群。
|
图 1 一维解空间中种群示意图 |
SPSO也是采用了基于种群的多模态寻优策略[8],但是SPSO直接在每一代粒子中选择种群种子,粒子在收敛过程中会有较剧烈的抖动[13],不利于算法的稳定收敛;而EMSPSO在pbest中选择种群种子,有效地利用了每一个粒子的“历史信息”,使得算法能够更加稳定地收敛。
标准PSO的代际更新公式如式(1)、(2),在经过数代进化后,粒子群会趋向一个全局最优点,从而不适应多模态优化的要求。为了使种群中的粒子都趋向于本种群适应度最优的位置,SPSO采用式(5)所示的速度更新公式[8]:
| $V_i^{k + 1} = \omega _i^k + {c_1}{r_1}\left( {pbest_i^k + X_i^k} \right) + {c_2}{r_2}\left( {X_i^k \cdot seed - X_i^k} \right)$ | (5) |
其中:Xik.seed为第k代中第i个粒子对应的种群种子,这一项的加入使得每一个种群中的粒子只向本种群种子的位置集中,实现了种群的独立进化。
但是式(5)所示的速度更新公式会导致每个粒子只关心本种群内部的信息与经验,各个种群之间没有交流。因粒子初始化位置的随机性,在粒子数目较少的情况下,可能会导致适应度较优的极值点被漏掉。为了改善这种情况,EMSPSO采用式(6)作为新的速度更新公式。
| $\begin{gathered} V_i^{k + 1} = \omega V_i^k + {c_1}{r_1}\left( {pbest_i^k - X_i^k} \right) + {c_2}{r_2}\left( {X_i^k \cdot seed - X_i^k} \right) + \hfill \\ {c_3}{r_3}\left( {gbes{t^k} - X_i^k} \right) \hfill \\ \end{gathered} $ | (6) |
其中:r3是[0,1]内的随机数,c3是加速度因子。改进的速度更新公式中全局最优项gbest的引入,使粒子在种群内收敛的同时还有向全局最优点收敛的趋势,通过合理设置c3的取值,可以使EMSPSO在保持种群多样性与快速收敛之间达到平衡,既可以不丢失适应度较优的极值点,又可以搜索到尽量多的极值。
在粒子群进化过程的后期,已经有较多的粒子收敛到所属种群的种子处,我们称这些粒子为冗余粒子[14]。冗余粒子具有十分相似的搜索行为,不仅对算法的搜索没有任何帮助,而且产生大量的计算开销,因此EMSPSO引入了冗余粒子重新初始化策略。其基本思路是:在每一代的粒子群中,遍历本代粒子群,找出所有冗余粒子,将其位置、速度、适应度值与pbest在解空间范围内重新随机初始化,使冗余粒子变为一个全新的粒子参与搜索。
冗余粒子重新初始化策略可以有效提高粒子的利用率,增强粒子群算法的全局搜索能力。尤其是在进化过程后期,此策略对算法整体性能的提升更加明显。
EMSPSO算法的具体步骤如下:
步骤1 初始化PSO中粒子位置和适应度、个体最优值pbest与全局最优值gbest,设置种群规模n、最大迭代次数Ngmax、种群距离σS、收缩因子χ与加速度因子c1、c2等参数。
步骤2 从当前代粒子群的所有粒子个体最优值pbest中选出种群种子,生成种群种子集合XS。
步骤3 根据本代群种子集合XS与本代全体粒子G生成本代种群。
步骤4 找出本代全体粒子G中的冗余粒子并将其重新初始化。
步骤5 根据式(6)与式(2)更新粒子群。
步骤6 计算更新后粒子群中每个粒子的适应度。
步骤7 更新粒子群个体最优值pbest与全局最优值gbest。
步骤8 完成本次迭代,判断是否满足终止条件(平均误差小于设定阈值或迭代次数超过最大代数),若满足,则停止循环输出结果;若不满足,返回步骤2继续循环,直至满足终止条件。
3 算法复杂度分析EMSPSO算法主要由选择种群种子、生成种群和冗余粒子初始化三个过程组成,要确定EMSPSO算法的计算复杂度,需要分别对这三个过程进行分析。
这三个过程的计算量主要花费在欧氏距离的计算上,因此其复杂度可以用计算欧氏距离的次数TE来衡量。在选择种群种子的过程中,需要将P中所有pbest按适应度从优到劣排序,若采用快速排序法,平均情况下的复杂度为O(n lg n)。外层循环须将所有粒子的pbest遍历一遍,共执行n次。内层循环中需要对XS中元素进行遍历,考虑最好的情况,σS足够大,XS中只含有一个元素,则只需要计算一次欧氏距离,TE=n;考虑最坏的情况,σS足够小,XS包含了所有粒子的pbest,则任意两个粒子之间都需要计算一次欧氏距离,TE=n(n-1)/2。这样就得到了TE的范围:
| $n \leqslant {T_{\text{E}}} \leqslant n\left( {n - 1} \right)/2$ | (7) |
记整个迭代过程中种子数目的最大值为nS,TE的范围可以满足更严格的关系式:
| $n \leqslant {T_{\text{E}}} \leqslant {\bar n_{\text{S}}} \cdot n$ | (8) |
所以,在选择种群种子的过程中,计算粒子间距离的平均复杂度介于O(n)与O(n2)之间,当nS≈n时,接近O(n2),当n
生成种群操作的过程与确定种群种子操作的过程极为相似,外层循环次数为n,内层循环次数最大为nS,计算欧氏距离的次数同样符合式(8),在一代中的平均计算复杂度为O(n2)。
在冗余粒子重新初始化的过程中,对每一个粒子都需要计算一次欧氏距离,因此在一次迭代中此过程的计算复杂度为O(n)。
假设EMSPSO算法进行了TP次迭代后终止,算法的整体复杂度为O((2×n2+n+n lg n)×TP)。SPSO的复杂度为O((n2+n lg n)×TP)[1],虽然EMSPSO比SPSO的计算复杂度有所增加,但具有较快的收敛速度与较高的求解精度,这在后面的实验对比分析中得到验证。
4 实验对比分析 4.1 测试函数为测试EMSPSO算法性能,验证改进策略的有效性,设计了EMSPSO与SPSO和SCGA的对比实验。本文实验环境为Intel Core i5-2430M CPU 2.4 GB,4 GB RAM的PC,操作系统为Windows 7.0,编程环境为Matlab 2011b。分别选取3个一维函数与3个二维函数作为测试函数进行分析,此6个测试函数在各自解空间中极值的个数与分布特性皆不相同。测试函数详细信息如表 1。
| 表 1 测试函数 |
在1维测试函数中,F1、F3为等峰函数,各有5个适应度为1.0的极大值,F1的极大值是均匀分布的,而F3的极大值不是均匀分布;F2为变峰函数,有5个适应度不同的极大值,最大适应度为1.0。在2维测试函数中,F4具有4个适应度为200的极大值,在解空间中分布较均匀。F5在解空间中含有若干极小值,在[0,0]处存在全局最小值0,其余极小值在最小值周围对称分布,任意两个相邻极值之间距离相等,测试中只关心前13个极小值。F6是比较困难的多模态测试函数,在解空间中同样存在若干极小值,这里只关心其中8个全局最小值与8个全局次小值。两个全局最小值与两个全局次小值为一组,整个解空间中存在4组极值,每组内的极值间距只有0.98,而两组间的距离远大于0.98,极值的不均匀分布与数量众多的局部极值点给算法的搜索带来很大挑战。
4.2 实验与结果分析实验选用精度、成功率与收敛速度三个评价标准对算法的性能进行对比。对某一极值点的寻优精度用可使用找到的极值点pi与实际的极值点opti适应度差值的绝对值来表示,其计算公式如式(9)。
| $ac{c_i} = \left| {f\left( {{p_i}} \right) - f\left( {op{t_i}} \right)} \right|$ | (9) |
在实验中规定单峰误差ε=0.001,当某一极值点的acci≤ε,才认为此极值点被搜索到。式(10)定义了算法的平均误差(Average ErrorS, AES)[15],N为适应度函数极值点的个数。AES体现了算法的全局平均精度,在一定的迭代次数下,平均误差越小,算法精度越高。
| $AES = \frac{1}{N}\sum\limits_{i = 1}^N {ac{c_i}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {f\left( {{p_i}} \right) - f\left( {op{t_i}} \right)} \right|} $ | (10) |
成功率指的是在进行多次实验后,能成功找到所有期望极值点的实验次数与实验总的次数的比值,是评价多模态寻优算法搜索性能的重要指标。
收敛速度通过计算搜索到所有期望的极值点所需要的平均评价次数与运行时间来确定。在一次运行中,搜索到一定精度的解所需要的评价次数与运行时间减少,收敛速度越高。
SCGA的交叉概率Pc=0.6,变异概率Pm=0.05[6];SPSO采用收缩因子PSO,收缩因子χ=0.729 8,c1=c2=2.05[8];EMSPSO使用与SPSO等价的参数,ω=χ,c1=c2=1.496 1,c3采用双曲正切函数tanh加速。
| ${c_3} = {c_{3\min }} + \left( {{c_{3\max }} - {c_{3\min }}} \right)\frac{{1 - \tanh \left( {k - 0.2N{g_{\max }}} \right)}}{2}$ | (11) |
其中:c3min=0,c3max=0.15,Ngmax为最大迭代次数,k为当前迭代次数。种群距离σS、种群规模n和Ngmax是与测试函数相关的参数,参考文献[1, 8]中参数的设置,其具体取值见表 2。
| 表 2 实验参数 |
在对比算法成功率的实验中,每一个测试函数都经过三种算法50次寻优,记录成功率如表 3的成功率。SCGA局部搜索能力较弱,容易出现个别极值点搜索精度较低的情况,所以对每一个测试函数的搜索成功率都没有达到100%。SPSO的局部搜索能力比SCGA要强,但是全局搜索能力较弱,对于一维函数与简单的二维函数F4,能保持100%的成功率;但对于极值点较多分布较复杂的F5、F6,成功率就会严重下降。而EMSPSO由于改进了速度更新公式,增加了冗余粒子初始化策略,提高了算法的搜索能力,对复杂函数的寻优成功率要高于SPSO。
| 表 3 三种算法对比 |
在算法精度的对比实验中,对每个测试函数都进行50次寻优,每次寻优都运行到此测试函数对应的最大迭代次数Ngmax,对50次实验的AES取平均值得到最终结果。由表 3平均误差AES可以看出,对每个测试函数,EMSPSO的平均误差AES远小于SCGA与SPSO。这说明,在相同迭代次数下,EMSPSO解的精度远高于其余两种算法,EMSPSO具有更强的局部搜索能力与较快的收敛速度。
在收敛速度的对比实验中,同样对每个测试函数进行50次寻优。规定平均误差的阈值εg=1E-4,在每次寻优时,当AES < εg时便停止迭代,记录此时的评价次数与运行时间,最后计算50次实验的平均值记录于表 3。实验结果表明,虽然增加了冗余粒子初始化策略,在一次迭代中的评价次数可能比其他两种算法更多,但EMSPSO的评价次数与运行时间在大部分情况下要少于SCGA与SPSO。这是由于EMSPSO具有更快的收敛速度,能在较少的迭代次数下搜索到平均误差小于εg的解。
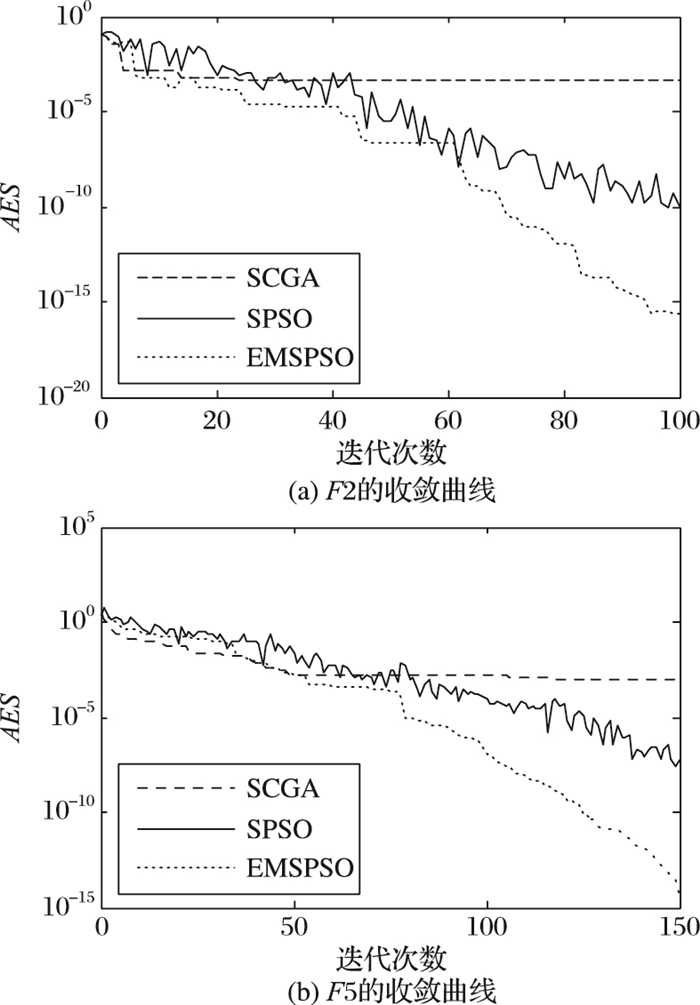
在图 2中,图(a)显示了一维函数F2的AES收敛曲线,图(b)显示了二维函数F5的AES收敛曲线。可以看出,无论是一维函数还是二维函数,EMSPSO的收敛速度要高于SCGA与SPSO。尤其是在进化后期,EMSPSO的搜索精度会快速提高,说明算法具有较好的局部搜索能力;而且,EMSPSO的收敛曲线几乎没有抖动,而SPSO有很大波动,这表明EMSPSO具有更好的稳定性。
|
图 2 三种算法AES的收敛曲线 |
为了提高多模态粒子群优化算法的搜索性能,平衡算法的开发与探索能力,提出了一种基于多种群的改进粒子群算法。该算法在SPSO的基础上改进了种群生成策略,提高了算法收敛的稳定性。并在迭代寻优的过程中引入了冗余粒子重新初始化策略,提高了粒子的利用率和算法的搜索效率。同时改进了速度更新公式,有效地避免遗漏适应度较优的极值点,使算法的开发与探索能力得到均衡。文章对EMSPSO算法的计算复杂度进行分析,并将其与SCGA和SPSO进行了对比实验。理论分析与实验结果表明,EMSPSO具有更好的多模态寻优性能,对于解决多模态函数优化问题具有收敛速度快、搜索精度高、稳定性好的优点。
| [1] |
吕明伟.基于相似度模型的多模态粒子群优化算法研究[D].大连:大连理工大学, 2013:10-13.
( LYU M W. Research on multimodal particle swarm optimization algorithm based on similarity model [D]. Dalian: Dalian University of Technology, 2013, 10-13
) ( 0) 0)
|
| [2] |
刘宇, 吕明伟, 李维佳, 等. 基于物种的自适应多模态粒子群优化算法[J].
山东大学学报(理学版), 2011, 46 (5) : 91-96.
( LIU Y, LYU M W, LI W J, et al. Adaptively species-based multimodal particle swarm optimization[J].
Journal of Shandong University (Natural Science), 2011, 46 (5) : 91-96.
) ( 0) 0)
|
| [3] |
KENNEDY J, EBERHART R. Particle swarm optimization [C]// Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ: IEEE, 1995, 4: 1942-1948.
( 0) 0)
|
| [4] |
HORN J. The nature of niching: genetic algorithm and the evolution of optimal, cooperative population [D]. Urbana-Champaign: University of Illinois at Urbana-Champaign, 1997: 17-21.
( 0) 0)
|
| [5] |
WEI L, ZHAO M. A niche hybrid genetic algorithm for global optimization of continuous multimodal functions[J].
Applied Mathematics and Computation, 2005, 160 (3) : 649-661.
doi: 10.1016/j.amc.2003.11.023 ( 0) 0)
|
| [6] |
LI J P, BALAZS M E, PARKS G T, et al. A species conserving genetic algorithm for multimodal function optimization[J].
Evolutionary Computation, 2002, 10 (3) : 207-234.
doi: 10.1162/106365602760234081 ( 0) 0)
|
| [7] |
陈娟, 徐立鸿. 动态小生境遗传算法在多模函数优化中的应用[J].
同济大学学报(自然科学版), 2006, 34 (5) : 684-688.
( CHEN J, XU L H. A dynamic niche genetic algorithm for multimodal function optimization[J].
Journal of Tongji University (Natural Science), 2006, 34 (5) : 684-688.
) ( 0) 0)
|
| [8] |
LI X. Adaptively choosing neighbourhood bests using species in a particle swarm optimizer for multimodal function optimization [M]// DEB K. Genetic and Evolutionary Computation—GECCO 2004, LNCS 3102. Berlin: Springer, 2004:105-116.
( 0) 0)
|
| [9] |
PASSARO A, STARITA A. Particle swarm optimization for multimodal function: a clustering approach[J].
Journal of Artificial Evolution and Application, 2008, 2008 (2) .
( 0) 0)
|
| [10] |
SEO J H, IM C H, HEO C G, et al. Multimodal function optimization based on particle swarm optimization[J].
IEEE Transactions on Magnetics, 2006, 42 (4) : 1095-1098.
doi: 10.1109/TMAG.2006.871568 ( 0) 0)
|
| [11] |
CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J].
IEEE Transactions on Evolutionary Computation, 2002, 6 (1) : 58-73.
doi: 10.1109/4235.985692 ( 0) 0)
|
| [12] |
GOLDBERG D E, RICHARDSON J. Genetic algorithms with sharing for multimodal function optimization [C]// Proceedings of the 2nd International Conference on Genetic Algorithms. Hillsdale, NJ: Lawrence Erlbaum Associates, 1987: 41-49.
( 0) 0)
|
| [13] |
IWAMATSU M. Multi-species particle swarm optimizer for multimodal function optimization[J].
IEICE Transactions on Information and Systems, 2006, E89-D (3) : 1181-1187.
doi: 10.1093/ietisy/e89-d.3.1181 ( 0) 0)
|
| [14] |
PARROTT D, LI X. Locating and tracking multiple dynamic optima by a particle swarm model using speciation[J].
IEEE Transactions on Evolutionary Computation, 2006, 10 (4) : 440-458.
doi: 10.1109/TEVC.2005.859468 ( 0) 0)
|
| [15] |
吴江, 胡捍英, 吴瑛. 面向应用的快速多峰寻优算法[J].
计算机应用研究, 2008, 25 (12) : 3617-3620.
( WU J, HU H Y, WU Y. Application-oriented fast optimizer for multi-peak searching[J].
Application Research of Computers, 2008, 25 (12) : 3617-3620.
) ( 0) 0)
|




