HE Jie, born in 1991. M. S. candidate. His research interests include MIMO communications.
XIAO Kun, born in 1974. Ph.D., associate professor. His research interests include wireless communications and mobile fading channels.
多径衰落和阴影效应是用来表征一般无线信道的两个特征。在复合无线信道模型中,Nakagami-m模型[1]和Suzuki模型[2]广泛地应用于各种无线通信系统中。然而这两种复合信道模型的概率密度函数(Probability Density Function, PDF)得不到闭式,给评估移动通信系统链路性能带来了很大的困难。广义K衰落信道模型不但能很好地模拟无线信道的快衰落和慢衰落效应,而且存在闭式,因而吸引了众多国内外学者的关注。
文献[3-4]分析了广义K衰落信道中多输入多输出(Multiple-Input Multiple-Output, MIMO)系统的容量。有关MIMO、单天线系统符号差错概率的研究可以在文献[5-7]中找到。由于正交空时分组编码可以提高系统的可靠性,并且使得接收端的解码相对简单[8-11],因此文献[12]和文献[13]在独立同分布(independent and necessarily identically distributed, i.i.d.)的广义K衰落信道中研究了采用正交空时分组编码的MIMO系统的性能。这些研究的不足在于:1)研究主要基于i.i.d.广义K衰落信道,而不是独立非同分布(independent but not necessarily identically distributed, i.n.i.d.)广义K衰落信道,而现实MIMO系统中,i.n.i.d.广义K衰落信道更具有一般性。本文接下来的研究结果将表明,i.n.i.d.广义K衰落信道和i.i.d.广义K衰落信道中的系统性能表达式截然不同,性能也存在显著差异。2)文献[14]研究了有限i.n.i.d.广义K衰落信道中最大比合并接收机的性能,即只考虑了波形参数m取不同正整数的情况,没有考虑波形参数k在MIMO子信道中的差异性,有较大的局限性,而且该研究不针对正交空时分组编码(Orthogonal Space Time Block Code, OSTBC)-MIMO系统。
基于上述原因,本文开展基于i.n.i.d.广义K衰落信道的OSTBC-MIMO系统的性能研究,同时考虑了波形参数m和k取不同正整数的情形。虽然要在数学上获得基于i.n.i.d.广义K衰落信道的OSTBC-MIMO系统性能的精确闭式非常困难,但是本文通过推导近似等效信噪比的概率密度函数,获得了OSTBC-MIMO系统的近似性能的闭式。在仿真分析中,着重考察了信道参数k对于系统性能的影响,并得出了科学的结论。
1 系统模型如图 1所示,在i.n.i.d.广义K衰落信道中,具有Nt个发射天线和Nr个接收天线的MIMO系统采用正交空时分组编码。首先,信源被调制成星座大小为M的正交振幅调制(Quadrature Amplitude Modulation, QAM)符号集合S,这些符号被OSTBC编码器编成大小为T×Nt的正交分组空时码C,T为正交分组空时码的分组长度。C可以表示为

|
图 1 系统模型 |
| $ \boldsymbol{Y} = \boldsymbol{CH} + \boldsymbol{n} $ | (1) |
其中:信道矩阵Η∈CNt×Nr,并假设在一个分组周期T内信道系数是不变的;信道矩阵中的元素hn, j=αn, jeiφn, j代表第n根发射天线到第j根接收天线间的信道系数,αn, j为相应子信道的幅值,服从i.n.i.d.广义K分布,φn, j是相应子信道的相位,服从(0,2π]的均匀分布。n是大小为T×Nr的噪声矩阵,其中的元素假定为服从
本文采用i.n.i.d.广义K衰落信道,第n根发射天线到第j根接收天线间子信道的波形参数kn, j和mn, j取任意的正整数,子信道幅值αn, j的PDF表示为:
| $ \begin{gathered} {f_{{a_{n,j}}}}\left( \alpha \right) = \frac{{4{m_{n,j}}^{\left( {{k_{n,j}}^{ + {m_n}},j} \right)/2}{\alpha ^{{k_{n,j}}^{ + {m_n}},j - 1}}}}{{\Gamma \left( {{m_{n,j}}} \right)\Gamma \left( {{k_{n,j}}} \right){\Omega _{n,j}}{{\left( {{k_{n,j}}^{ + {m_n}},j} \right)}^{/2}}}}{K_{{k_n}}},{j^{ - {m_n}}},j \cdot \hfill \\ \left( {2{{\left( {{m_{n,j}}/{\Omega _{n,j}}} \right)}^{1/2}}\alpha } \right) \hfill \\ \end{gathered} $ | (2) |
其中:kn, j和mn, j是第n根发射天线到第j根接收天线间子信道的波形参数,取任意的正整数;参数kn, j反映阴影效应,且与阴影效应的严重程度成反比;参数mn, j反映多径衰落,且与多径衰落的严重程度成反比;Ωn, j=E
根据文献[15]的式(6),输出端的等效信噪比(Signal-to-Noise Ratio, SNR)可以表示为:
| $ {\gamma ^{{\text{OSTBC}}}} = \sum\limits_{n = 1}^{{N_t}} {\sum\limits_{j = 1}^{{N_r}} {{\gamma _{n,j}}} } $ | (3) |
其中:
| $ {\gamma ^{{\text{OSTBC}}}} = \sum\limits_{l = 1}^L {{\gamma _l}} $ | (4) |
其中:
| $ {{\bar \gamma }_l} = {\text{E}}\left[ {{\gamma _l}} \right] $ | (5) |
其中:E[]表示数学期望。将
| $ {{\bar \gamma }_l} = {\text{E}}\left[ {\frac{{\bar \gamma \alpha _l^2}}{{{N_t}{R_c}}}} \right] = \frac{{\bar \gamma {\text{E}}\left[ {\alpha _l^2} \right]}}{{{N_t}{R_c}}} $ | (6) |
将
| $ {{\bar \gamma }_l} = \frac{{\bar \gamma {k_l}{\Omega _l}}}{{{N_t}{R_c}}} $ | (7) |
利用式(7)和
| $ \frac{{{\text{d}}{\alpha _l}}}{{{\text{d}}{\gamma _l}}} = \frac{1}{2} \times {\left( {\frac{{{\gamma _l}{N_t}{R_c}}}{{\bar \gamma }}} \right)^{ - \frac{1}{2}}}\frac{{{N_t}{R_c}}}{{\bar \gamma }} $ | (8) |
于是,子信道的瞬时信噪比γl的PDF可以表示为:
| $ {f_{{\gamma _l}}}\left( \gamma \right) = {f_{\alpha l}}\left( {{{\left( {\frac{{{\gamma _l}{N_t}{R_c}}}{{\bar \gamma }}} \right)}^{\frac{1}{2}}}} \right) \times \left| {\frac{{{\text{d}}{\alpha _l}}}{{{\text{d}}{\gamma _l}}}} \right| $ | (9) |
其中: fαl(x)为子信道幅值αl的PDF,服从式(2)。将fαl(x)和
| $ \begin{array}{*{20}{c}} {{f_{{\gamma _l}}}\left( \gamma \right) = \frac{{4m_l^{\left( {{k_l} + ml} \right)/2}}}{{\Gamma \left( {{m_1}} \right)\Gamma \left( {{k_1}} \right)\Omega _l^{\left( {{k_l} + {m_l}} \right)/2}}}{{\left( {\frac{{{\gamma _l}{N_t}{R_c}}}{{\bar \gamma }}} \right)}^{\left( {{k_l} + ml - 1} \right)/2}} \times } \\ {{K_{{k_l} - {m_l}}}\left( {2{{\left( {\frac{{{m_l}}}{{{\Omega _l}}} \times \frac{{\gamma {N_t}{R_c}}}{{\bar \gamma }}} \right)}^{1/2}}} \right) \times \frac{1}{2}{{\left( {\frac{{\gamma {N_t}{R_c}}}{{\bar \gamma }}} \right)}^{ - \frac{1}{2}}}\frac{{{N_t}{R_c}}}{{\bar \gamma }}} \\ {\frac{{2{{\left( {\frac{{{m_l}{N_t}{R_c}}}{{{\Omega _l}\bar \gamma }}} \right)}^{\left( {kl + {m_l}} \right)/2}}}}{{\Gamma \left( {{m_l}} \right)\Gamma \left( {{k_l}} \right)}}{\gamma ^{\frac{{kl + {m_l}}}{2} - 1}}{K_{kl - {m_l}}}\left( {2{{\left( {\frac{{\gamma {m_l}{N_t}{R_c}}}{{{\Omega _l}\bar \gamma }}} \right)}^{1/2}}} \right)} \end{array} $ | (10) |
根据式(7),可以表示为:
| $ \bar \gamma {\text{ = }}\frac{{{{\bar \gamma }_t}{N_t}{R_c}}}{{{k_l}{\Omega _l}}} $ | (11) |
将上式代入fγl(γ),于是得到:
| $ {f_{{\gamma _l}}}\left( \gamma \right) = \frac{{2{{\left( {\frac{{{k_l}{m_l}}}{{{{\bar \gamma }_l}}}} \right)}^{\frac{{\left( {{k_l} + {m_l}} \right)}}{2}}}{\gamma ^{\left( {\frac{{\left( {{k_l} + {m_l}} \right)}}{2} - 1} \right)}}}}{{\Gamma \left( {{m_1}} \right)\Gamma \left( {{k_1}} \right)}}{K_{{k_l} + {m_l}}}\left( {2\sqrt {\frac{{{k_l}{m_l}}}{{{{\bar \gamma }_l}}}\gamma } } \right) $ | (12) |
从公式
假设两个独立的伽马随机变量xl~(x; μx, ηx),yl~(y; μy, ηy),xl和yl的PDF分别表示为:
| $ {f_G}\left( {x;{\mu _x},{\eta _x}} \right) = \frac{{{x^{{\mu _{{x^{ - 1}}}}}}}}{{{\eta _x}^{{\mu _x}}\Gamma \left( {{\mu _x}} \right)}}\exp \left( { - \frac{x}{{{\eta _x}}}} \right);x \geqslant 0 $ | (13) |
| $ {f_G}\left( {y;{\mu _y},{\eta _y}} \right) = \frac{{{x^{{\mu _{{y^{ - 1}}}}}}}}{{{\eta _y}^{{\mu _y}}\Gamma \left( {{\mu _y}} \right)}}\exp \left( { - \frac{x}{{{\eta _y}}}} \right);y \geqslant 0 $ | (14) |
令随机变量zl等于xl和yl的乘积,即zl=xlyl,于是zl的PDF为:
| $ \begin{array}{*{20}{l}} {{f_{{z_l}}}\left( {{z_l}} \right) = \int_0^\infty {\frac{1}{x}{f_G}\left( {x;{\mu _x},{\eta _x}} \right){f_G}\left( {\frac{{{z_l}}}{x};{\mu _y},{\eta _y}} \right){\text{d}}x = } } \\ {\int_0^\infty {\frac{1}{x}\frac{{{x^{{\mu _{{x^{ - 1}}}}}}}}{{{\eta _x}^{{\mu _x}}\Gamma \left( {{\mu _x}} \right)}}\exp \left( { - \frac{x}{{{\eta _x}}}} \right)\frac{{{{\left( {{z_l}/x} \right)}^{{\mu _{{y^{ - 1}}}}}}}}{{{\eta _y}^{{\mu _y}}\Gamma \left( {{\mu _y}} \right)}}\exp \left( { - \frac{{{z_l}/x}}{{{\eta _y}}}} \right){\text{d}}x = } } \\ {\frac{{{{\left( {{z_l}} \right)}^{^{{\mu _{{y^{ - 1}}}}}}}}}{{\Gamma \left( {{\mu _y}} \right){\eta _y}^{{\mu _y}}\Gamma \left( {{\mu _x}} \right){\eta _x}^{{\mu _x}}}}\int_0^\infty {{x^{{\mu _x} - {\mu _y} - 1}}} \exp \left( { - \frac{x}{{{\eta _x}}} - \frac{{{z_l}}}{{x{\eta _y}}}} \right){\text{d}}x} \end{array} $ | (15) |
根据文献[15]中的式(3.471.9),可以得到闭式:
| $ {f_{{z_l}}}\left( {{z_l}} \right) = \frac{{2{{\left( {{z_l}} \right)}^{\frac{{{\mu _x} + {\mu _y}}}{2} - 1}}}}{{\Gamma \left( {{\mu _x}} \right)\Gamma \left( {{\mu _y}} \right)}}{\left( {\frac{1}{{{\eta _x}{\eta _y}}}} \right)^{\frac{{{\mu _x} + {\mu _y}}}{2}}}{K_{{\mu _x} - {\mu _y}}}\left( {2\sqrt {\frac{{{z_l}}}{{{\eta _x}{\eta _y}}}} } \right) $ | (16) |
令μx=k,ηx=1/k,μy=m以及ηy=/m,代入上式后得到:
| $ {f_{{z_l}}}\left( {{z_l}} \right) = \frac{{2{{\left( {{z_l}} \right)}^{\frac{{k + m}}{2} - 1}}}}{{\Gamma \left( k \right)\Gamma \left( m \right)}}{\left( {\frac{{km}}{{\bar \gamma }}} \right)^{\frac{{k + m}}{2}}}{K_{k - m}}\left( {2\sqrt {\frac{{km}}{{\bar \gamma }}{z_l}} } \right) $ | (17) |
可见,xl和yl的乘积的PDF与式(12)相同,即随机变量γl=xlyl。于是等效信噪比γOSTBC可以改写为:
| $ {\gamma ^{{\text{OSTBC}}}} = \sum\limits_{l = 1}^L {{\gamma _l}} = \sum\limits_{l = 1}^L {{x_l}{y_l}} $ | (18) |
根据文献[14]中的式(10),γOSTBC可以近似表示为:
| $ {\gamma ^{{\text{OSTBC}}}} = \sum\limits_{l = 1}^L {{\gamma _l}} = \sum\limits_{l = 1}^L {{x_l}{y_l}} \approx \frac{{\left( {\sum\limits_{l = 1}^L {{x_l}} } \right)\left( {\sum\limits_{l = 1}^L {{y_l}} } \right)}}{L} = {s_1}{s_2} $ | (19) |
其中:
| $ {f_{{s_1}}}\left( x \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right){f_G}\left( {x;j,\frac{{{\beta _i}}}{L}} \right)} } $ | (20) |
| $ {f_{{s_2}}}\left( x \right) = \sum\limits_{i = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right){f_G}\left( {x;s,\frac{{{{\bar \gamma }_l}}}{{{m_l}}}} \right)} } $ | (21) |
其中: βi=1/ki。上面公式中的系数wL在文献[14]的式(24)和(25)中作了定义。本文为了便于估算和简化,采用文献[14]中的递推表达式:
| $ \begin{array}{*{20}{l}} {{w_L}\left( {i,{k_i} - t,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right) = \frac{1}{t}\sum\limits_{\begin{array}{*{20}{c}} {q = 1} \\ {q \ne i} \end{array}}^L {\sum\limits_{j = 1}^t {\frac{{{k_q}}}{{\beta _i^j}} \times } } } \\ {{{\left( {\frac{1}{{{\beta _i}}} - \frac{1}{{{\beta _q}}}} \right)}^{ - j}}{w_L}\left( {i,{k_i} - t + j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)} \end{array} $ | (22) |
和
| $ {w_L}\left( {i,{k_i},\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right) = \frac{{\beta _i^{{k_i}}}}{{\prod\limits_{h = 1}^L {\beta _h^{{k_h}}} }}\prod\limits_{\begin{array}{*{20}{c}} {j = 1} \\ {j \ne i} \end{array}}^L {{{\left( {\frac{1}{{{\beta _j}}} - \frac{1}{{{\beta _i}}}} \right)}^{ - {k_j}}}} $ | (23) |
其中:t=1, 2, …, ki-1。令
| $ {f_{{\gamma ^{{\text{OSTBC}}\left( Z \right)}}}} = \int_0^\infty {\frac{1}{x}{f_{{s_1}}}\left( x \right)} {f_{{s_2}}}\left( {z/x} \right){\text{d}}x $ | (24) |
将式(20)和(21)代入式(24)中,式(24)可以进一步表示为:
| $ \begin{array}{*{20}{l}} {{f_{{\gamma ^{{\text{OSTBC}}}}}}\left( z \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)} } } } \times } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right)} \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {\frac{1}{x}{f_G}\left( {x;j,{\beta _i}/L} \right){f_G}\left( {z/x;s,{{\bar \gamma }_l}/{m_l}} \right){\text{d}}x} } \end{array} $ | (25) |
将伽马随机变量的PDF即式(13)代入式(25),可以得到:
| $ \begin{array}{*{20}{l}} {{f_{{\gamma ^{{\rm{OSTBC}}}}}}\left( z \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{{{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right){w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right)}}{{\Gamma \left( s \right)\Gamma \left( j \right)}} \times \left( {\frac{L}{{{\beta _i}}}} \right)} } } } }\\ {{{\left( {\frac{{{m_l}}}{{{{\bar \gamma }_l}}}} \right)}^s}{z^{s - 1}}\int_0^\infty {{x^{j - s - 1}}} \exp \left( { - \frac{L}{{{\beta _i}}}x - \frac{{z{m_l}}}{{x{{\bar \gamma }_l}}}} \right){\rm{d}}x} \end{array} $ | (26) |
接着,利用文献[15]中的式(3.471.9)可以得到闭合解析式:
| $ \begin{array}{*{20}{l}} {{f_{{\gamma ^{{\text{OSTBC}}}}}}\left( z \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)} } } } \times } \\ {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right)\frac{{2\Xi _{il}^{\frac{{\left( {j + s} \right)}}{2}}{z^{\frac{{\left( {j + s} \right)}}{2} - 1}}}}{{\Gamma \left( s \right)\Gamma \left( j \right)}}{K_{j - s}}\left( {2\sqrt {{\Xi _{il}}z} } \right)} \end{array} $ | (27) |
式(27)为γOSTBC的近似等效信噪比的PDF表达式。由于精确的等效信噪比γOSTBC的PDF表达式很难得到,因此利用γOSTBC的近似等效信噪比可以表示为两个由多个独立伽马随机变量之和构成的随机变量的乘积这一关系,推导出近似等效信噪比的PDF表达式。从第3部分的数值结果来看,其近似效果是理想的。
2.2 平均符号差错概率根据文献[16]中的式(19),在i.n.i.d.广义K衰落信道中,采用M=I×J阶QAM调制并经过正交空时分组编码的MIMO系统的平均符号差错概率可以表示为:
| $ \begin{array}{*{20}{l}} {\bar P_s^{{\text{OSTBC}}}\left( E \right) = \int_0^\infty {P_s^{{\text{STBC}}}\left( {E|{\gamma ^{{\text{OSTBC}}}} = \gamma } \right){f_{{\gamma ^{{\text{OSTBC}}}}}}\left( \gamma \right){\text{d}}\gamma = } } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2q\left( I \right){I_1}\left( {g_{{\text{QAM}}}^R\left( {I,J;\xi } \right){\gamma ^{{\text{OSTBC}}}}} \right) + } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2q\left( J \right){I_1}\left( {g_{{\text{QAM}}}^R\left( {I,J;\xi } \right)\xi {\gamma ^{{\text{OSTBC}}}}} \right) - 4q\left( I \right)q\left( J \right) \times } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {I_2}\left( {g_{{\text{QAM}}}^R\left( {I,J;\xi } \right){\gamma ^{{\text{OSTBC}}}},g_{{\text{QAM}}}^R\left( {I,J;\xi } \right)\xi {\gamma ^{{\text{OSTBC}}}}} \right)} \end{array} $ | (28) |
其中:q(x)=1-x-1;ξ=dJ2/dI2为同向和正交判决距离的平方的比值;gQAMR(I, J; ξ)=3/[(I2-1)+(J2-1)ξ];I1(A)和I2(A1, A2)如式(29)、(30):
| $ {I_1}\left( A \right) = \int_0^\infty {Q\left( {\sqrt {1A\gamma } } \right){f_{{\gamma ^{{\text{OSTBC}}}}}}\left( \gamma \right){\text{d}}\gamma } $ | (29) |
| $ {I_2}\left( {{A_{1,}}{A_2}} \right) = \int_0^\infty {Q\left( {\sqrt {2{A_1}\gamma } } \right)Q\left( {\sqrt {2{A_2}\gamma } } \right){f_{{\gamma ^{{\text{OSTBC}}}}}}\left( \gamma \right){\text{d}}\gamma } $ | (30) |
其中:Q(x)为高斯Q函数[16]。把式(27)代入式(29),I1(A)可以表示为:
| $ \begin{array}{*{20}{l}} {{I_1}\left( A \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)} } } } \times } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right)\frac{{2\Xi _{il}^{\left( {j + s} \right)/2}}}{{\Gamma \left( s \right)\Gamma \left( j \right)}} \times } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {Q\left( {\sqrt {2{A_1}\gamma } } \right) \times {\gamma ^{\frac{{\left( {j + s} \right)}}{2} - 1}}{K_{j - s}}\left( {2\sqrt {{\Xi _{il}}\gamma } } \right){\text{d}}\gamma } } \end{array} $ | (31) |
接着,利用文献[6]中的式(8),可得到闭合表达式:
| $ \begin{array}{*{20}{l}} {{I_1}\left( A \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{{{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)}}{{\left( {2\sqrt \pi \Gamma \left( s \right)\Gamma \left( j \right)} \right)}}} } } } \times } \\ {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right)G_{2,3}^{2,2}\left[ {\frac{{{\Xi _{ij}}}}{A}\left| {\begin{array}{*{20}{l}} {1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1/2} \\ {j,{\kern 1pt} {\kern 1pt} {\kern 1pt} s,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \end{array}} \right.} \right]} \end{array} $ | (32) |
把式(27)代入式(30),并且将里面的Q(x)函数和贝塞尔K(x)函数用Meijer’s G函数表示(参见文献[17]中的式(03.04.26.0009.01)和(06.27.26.0006.01)),I2(A1, A2)可以表示为:
| $ \begin{array}{*{20}{l}} {{I_1}\left( {{A_1}{A_2}} \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)} } } } \times } \\ {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right)\frac{{\Xi _{il}^{\left( {j + s} \right)/2}}}{{4\pi \Gamma \left( s \right)\Gamma \left( j \right)}} \times } \\ {\int_0^\infty {{\gamma ^{\frac{{\left( {j + s} \right)}}{2} - 1}}G_{0,2}^{2,0}\left( {{\Xi _{ij}}\gamma |\frac{{j - s}}{2}\frac{{s - j}}{2}} \right) \times } } \\ {G_{1,2}^{2,0}\left( {{A_2}\gamma \left| {\begin{array}{*{20}{l}} 1 \\ {0,0.5} \end{array}} \right.} \right)G_{1,2}^{2,0}\left( {{A_1}\gamma \left| {\begin{array}{*{20}{l}} 1 \\ {0,0.5} \end{array}} \right.} \right){\text{d}}\gamma } \end{array} $ | (33) |
利用文献[17]中的式(07.34.21.0081.01),式(33)可以简化为:
| $ \begin{array}{*{20}{l}} {{I_2}\left( {{A_1},{A_2}} \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{1}{{\left( {4\pi \cdot \Gamma \left( s \right)\Gamma \left( j \right)} \right)}} \times } } } } } \\ {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right){w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right) \times } \\ {G_{2,0:1,2:1,2}^{0,2:2,0:2,0}\left[ {1 - j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 - s\left| {\begin{array}{*{20}{l}} 1 \\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.5} \end{array}\left| {\begin{array}{*{20}{l}} 1 \\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.5} \end{array}} \right.\left| {\frac{{{A_1}}}{{{\Xi _{il}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{A_2}}}{{{\Xi _{il}}}}} \right.} \right.} \right]} \end{array} $ | (34) |
其中,
于是,用式(32)和(34)替换式(28)中的I1(A)和I2(A1, A2),得到平均符号差错概率如式(35)所示。
| $ \begin{array}{*{20}{l}} {\bar P_s^{{\rm{OSTBC}}}\left( E \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{1}{{\sqrt \pi \Gamma \left( s \right)\Gamma \left( j \right)}}} } } } {w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right){w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right) \times }\\ {\left\{ {\left( {1 - {I^{ - 1}}} \right)G_{2,3}^{2,2}\left[ {\frac{{{\Xi _{il}}}}{{g_{{\rm{QAM}}}^R\left( {I,J,\xi } \right)}}\left| {\begin{array}{*{20}{l}} {1,1/2}\\ {j,s,0} \end{array}} \right.} \right]} \right. + }\\ {\left( {1 - {J^{ - 1}}} \right)G_{2,3}^{2,2}\left[ {\frac{{{\Xi _{il}}}}{{g_{{\rm{QAM}}}^R\left( {I,J,\xi } \right)\xi }}\left| {\begin{array}{*{20}{l}} {1,1/2}\\ {j,s,0} \end{array}} \right.} \right] - \frac{{\left( {1 - {I^{ - 1}}} \right)\left( {1 - {J^{ - 1}}} \right)}}{{\sqrt \pi }}G_{2,0:1,2:1,2}^{0,2:2,0:2,0}}\\ {\left. {\left[ {1 - j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 - s\left| {\begin{array}{*{20}{l}} 1\\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1/2} \end{array}\left| {\begin{array}{*{20}{l}} 1\\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1/2} \end{array}} \right.\left| {\frac{{g_{{\rm{QAM}}}^R\left( {I,J,\xi } \right)}}{{{\Xi _{il}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{g_{{\rm{QAM}}}^R\left( {I,J,\xi } \right)\xi }}{{{\Xi _{il}}}}} \right.} \right.} \right]} \right\}} \end{array} $ | (35) |
本文中的中断概率定义为:当等效信噪比γOSTBC低于中断门限γth时,系统发生中断。于是,中断概率表达式为:
| $ {P_{{\text{out}}}}\left( {{\gamma _{th}}} \right) = \int_0^{{\gamma _{th}}} {{f_{{\gamma ^{{\text{OSTBC}}}}}}\left( x \right){\text{d}}x} $ | (36) |
将式(27)代入式(36),后者可以表示为:
| $ \begin{array}{*{20}{l}} {{P_{{\text{out}}}}\left( {{\gamma _{th}}} \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right) \times } } } } } \\ {\frac{{2\Xi _{il}^{\left( {j + s} \right)/2}}}{{\Gamma \left( s \right)\Gamma \left( j \right)}}{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right) \times } \\ {\int_0^{{\gamma _{th}}} {{z^{\frac{{\left( {j + s} \right)}}{2} - 1}}} {K_{j - s}}\left( {2\sqrt {{\Xi _{il}}z} } \right){\text{d}}z} \end{array} $ | (37) |
根据文献[14]中的式(5),中断概率最终表示为:
| $ \begin{array}{*{20}{l}} {{P_{{\text{out}}}}\left( {{\gamma _{th}}} \right) = \sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{{{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right)}}{{\Gamma \left( s \right)\Gamma \left( j \right)}} \times } } } } } \\ {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right)G_{1,3}^{2,1}\left[ {{\Xi _{il}}{\gamma _{th}}\left| {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \\ {j,s,0} \end{array}} \right.} \right]} \end{array} $ | (38) |
根据文献[13]中的式(16),在广义K衰落信道中,采用正交空时分组编码的香侬容量定义为:
| $ C = \frac{{{R_c}}}{{\ln }}{\text{E}}\left[ {\ln \left( {1 + \frac{{\bar \gamma }}{{{N_t}{R_c}}}\left\| H \right\|_{\text{F}}^2} \right)} \right] $ | (39) |
‖·‖F表示弗罗贝尼乌斯范数。由式(4)以及
| $ {\gamma ^{{\text{OSTBC}}}} = \sum\limits_{l = 1}^L {{\gamma _l}} = \frac{{\bar \gamma }}{{{N_t}{R_c}}}\sum\limits_{l = 1}^L {\alpha _l^2} = \frac{{\bar \gamma }}{{{N_t}{R_c}}}\left\| \boldsymbol{H} \right\|_{\text{F}}^2 $ | (40) |
将式(40)代入式(39),展开数学期望,后者简化为:
| $ C = \frac{{{R_c}}}{{\ln 2}}\int_0^\infty {\ln \left( {1 + \gamma } \right){f_{{\gamma ^{{\text{OSTBC}}}}}}\left( \gamma \right){\text{d}}\gamma } $ | (41) |
利用文献[17]中的式(01.04.26.0003.01)和(03.04.26.0006.01),对数函数ln(1+γ)用Meijer's G函数表示,并将式(27)代入式(41),容量可以表示为:
| $ \begin{array}{*{20}{l}} {C = \frac{{{R_c}}}{{\ln 2}}\sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right) \times } } } } } \\ {\frac{1}{{\Gamma \left( s \right)\Gamma \left( j \right)}}{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {{{\bar \gamma }_q}/{m_q}} \right\}_{q = 1}^L} \right) \times } \\ {\int_0^\infty {G_{2,2}^{1,2}} \left[ {\gamma \left| {\begin{array}{*{20}{c}} {1,1} \\ {1,0} \end{array}} \right.} \right]\frac{{2\Xi _{il}^{\left( {j + s} \right)/2}}}{{\Gamma \left( s \right)\Gamma \left( j \right)}}{\gamma ^{\frac{{\left( {s + j} \right)}}{2} - 1}}{K_{j - s}}\left( {2\sqrt {{\Xi _{il}}} \gamma } \right){\text{d}}\gamma } \end{array} $ | (42) |
根据文献[15]中的式(7.813.1),可以得到闭合解析式:
| $ \begin{array}{*{20}{l}} {C = \frac{{{R_c}}}{{\ln 2}}\sum\limits_{i = 1}^L {\sum\limits_{j = 1}^{{k_i}} {\sum\limits_{l = 1}^L {\sum\limits_{s = 1}^{{m_i}} {\frac{1}{{\Gamma \left( s \right)\Gamma \left( j \right)}}{w_L}\left( {i,j,\left\{ {{k_q}} \right\}_{q = 1}^L,\left\{ {{\beta _q}} \right\}_{q = 1}^L} \right) \times } } } } } \\ {{w_L}\left( {l,s,\left\{ {{m_q}} \right\}_{q = 1}^L,\left\{ {\frac{{{{\bar \gamma }_q}}}{{{m_q}}}} \right\}_{q = 1}^L} \right)G_{2,4}^{4,1}\left[ {{\Xi _{il}}\left| {\begin{array}{*{20}{c}} {0,1} \\ {J,S,0,0} \end{array}} \right.} \right]} \end{array} $ | (43) |
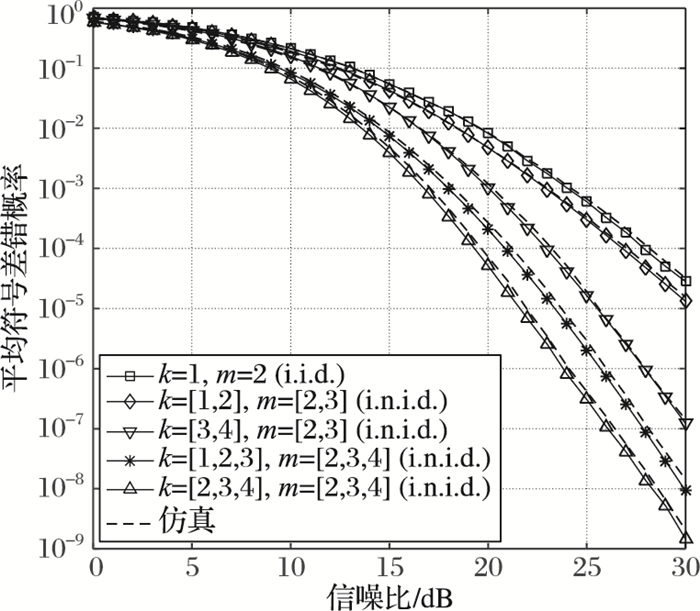
本节通过蒙特卡洛仿真验证理论推导的正确性以及获得系统性能数据。产生1010个i.n.i.d.广义K分布随机数,根据式(4)、(5),得到输出端的等效信噪比。图 2描绘了i.n.i.d.广义K衰落信道中OSTBC-MIMO系统在16-QAM调制下的平均符号差错概率与信噪比的关系,其中发射天线数分别为2和3,接收天线数为1。可以看出当增加发射天线数目时,平均符号差错概率有了明显的减小。至于信道参数kl对平均符号差错概率的影响,通过在相同的仿真设置下,仅改变参数kl的取值来考察平均符号差错概率。图 2中,在发射天线数为2且参数ml不变的情况下,kl=1, 2时的平均符号差错概率比kl=3, 4时的平均符号差错概率大。相同的结论在发射天线数为3的数据中也观察到。这说明当参数kl增大时,各子信道的信道状况变好导致平均符号差错概率变小,可见参数kl对平均符号差错概率有着显著的影响。
|
图 2 理论和仿真的平均符号差错概率对比 |
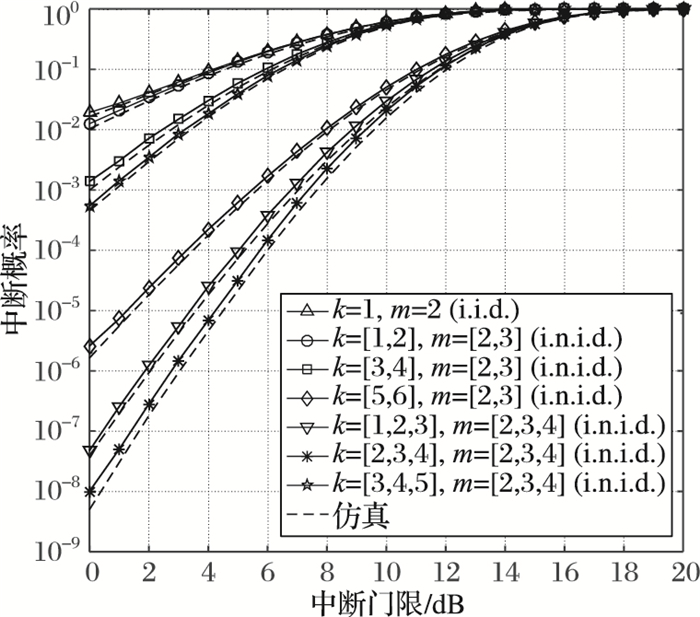
图 3给出了i.n.i.d.广义K衰落信道中,OSTBC-MIMO系统在16-QAM调制下中断概率与中断门限γth的关系。可以观察到理论和仿真的高度吻合。同样仿真了参数ml不变,参数kl取不同数值的情形。从图 3可以看到,随着参数kl的增大,系统的中断概率呈现明显的下降,这也说明了反映阴影效应严重程度的参数kl对系统中断概率有着重要的影响。
|
图 3 理论和仿真的中断概率对比 |
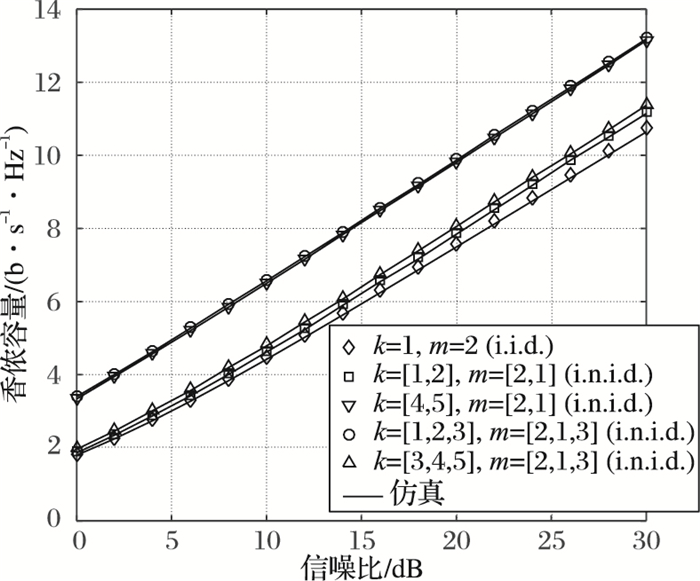
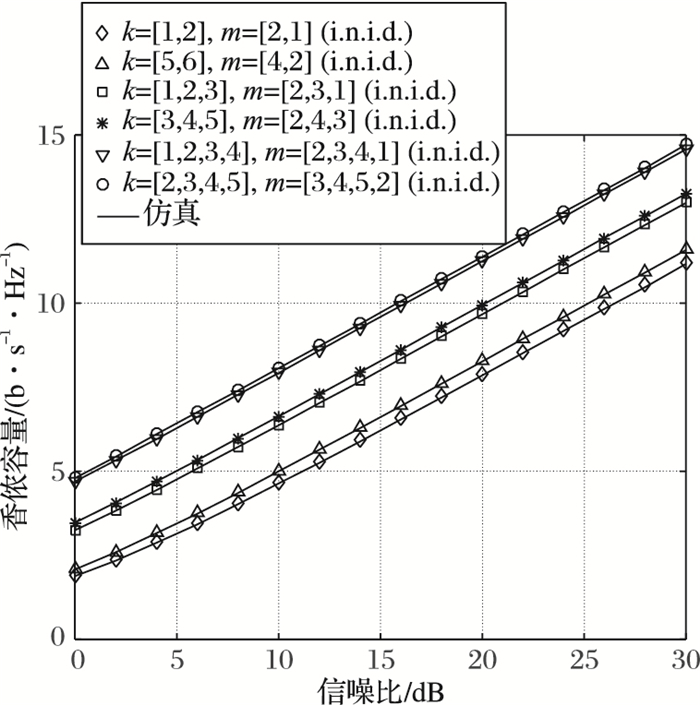
图 4和图 5描绘了i.n.i.d.广义K衰落信道中,OSTBC-MIMO系统在16-QAM调制下的信噪比和容量的关系。同样可以发现,理论和仿真结果是吻合的。图 4中,在相同的发射天线数下,当信道参数ml不变时,随着参数kl的变大容量略微增大;而图 5展示了参数ml和kl同时增大时的香侬容量。此外,从图 4和图 5观察到,当发射天线数增加时,容量也有明显的增长。
|
图 4 ml不变、kl变大时理论和仿真的容量对比 |
|
图 5 ml和kl同时增大时理论和仿真的容量对比 |
本文通过在独立非同分布广义K衰落信道中获得近似等效信噪比的PDF闭式解决了等效信噪比的精确PDF闭式难以获得,进而不能获得基于独立非同分布广义K衰落信道的OSTBC-MIMO系统性能闭式这一问题。所得到的平均符号差错概率、中断概率以及容量的闭式性能与仿真结果高度一致,从而验证了理论分析的正确性。需要重视的是,数值分析表明波形参数k在平均符号差错概率和中断概率上的影响是显著的,在容量上存在细微影响,然而已有的研究往往忽略了参数k在实际MIMO子信道中的差异对系统性能的影响,本文的工作完善了这一理论问题,具有一般性,取得了积极的进展。
| [1] |
UJJINIMATAD R, PATIL S R. Signal detection in cognitive radio networks over AWGN, Nakagami-m and Nakagami-q channels [C]// Proceedings of the 2014 11th International Conference on Wireless and Optical Communications Networks. Piscataway, NJ: IEEE, 2014:1-5.
( 0) 0)
|
| [2] |
BACHA M, HASSAN S A. Distributed versus cluster-based cooperative linear networks: a range extension study in Suzuki fading environments [C]// Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. Piscataway, NJ: IEEE, 2013: 976-980.
( 0) 0)
|
| [3] |
TRIGUI I, AFFES S, STEPHENNE A. Analysis of relay capacity over generalized-K fading channels with cochannel interference [C]// Proceedings of the 2014 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: IEEE, 2014: 144-148.
( 0) 0)
|
| [4] |
JUNG J, LEE S R, PARK H, et al. Capacity and error probability analysis of diversity reception schemes over generalized-K fading channels using a mixture gamma distribution[J].
IEEE Transactions on Wireless Communications, 2014, 13 (9) : 4721-4730.
doi: 10.1109/TWC.2014.2331691 ( 0) 0)
|
| [5] |
GUPTA S, KATIYAR H. Outage performance of regenerative cooperative relay network in KG fading channel [C]// Proceedings of the 2014 20th National Conference on Communications. Piscataway, NJ: IEEE, 2014: 1-5.
( 0) 0)
|
| [6] |
BITHAS P S, SAGIAS N C, MATHIOPOULOS P T, et al. On the performance analysis of digital communications over generalized-K fading channels[J].
IEEE Communications Letters, 2006, 10 (5) : 353-355.
doi: 10.1109/LCOMM.2006.1633320 ( 0) 0)
|
| [7] |
LI X, LI L, SU X. Approximate capacity analysis for distributed MIMO system over generalized-K fading channels [C]// Proceedings of the 2015 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: IEEE, 2015:235-240.
( 0) 0)
|
| [8] |
张红霞, 戴居丰. 3GPP信道模型中STBC-OFDM系统性能分析[J].
计算机应用, 2009, 29 (10) : 2614-2616.
( ZHANG H X, DAI J F. Performance of STBC-OFDM system in 3GPP channel model[J].
Journal of Computer Applications, 2009, 29 (10) : 2614-2616.
doi: 10.3724/SP.J.1087.2009.02614 ) ( 0) 0)
|
| [9] |
YOON C, LEE H, KANG J. Effect of generalized-K fading on the performance of symmetric coordinate interleaved orthogonal designs[J].
IEEE Communications Letters, 2014, 18 (4) : 588-591.
doi: 10.1109/LCOMM.2014.021014.132555 ( 0) 0)
|
| [10] |
ARTI K M K, MALLIK R K, SCHOBER R. Performance analysis of OSTBC relaying in AF MIMO relay systems with imperfect CSI[J].
IEEE Transactions on Vehicular Technology, 2015, 64 (7) : 3291-3298.
( 0) 0)
|
| [11] |
CHEN H, WANG Z J. SER of orthogonal space-time block codes over Rician and Nakagami-m RF backscattering channels[J].
IEEE Transactions on Vehicular Technology, 2014, 63 (2) : 654-663.
doi: 10.1109/TVT.2013.2280598 ( 0) 0)
|
| [12] |
LEGNAIN R M, HAFEZ R H M, MARSLAND I D. Multiuser detection for Rate-1/2 OSTBC with four transmit antennas [C]// Proceedings of the 2013 1st International Conference on Communications, Signal Processing, and their Applications. Piscataway, NJ: IEEE, 2013: 1-4.
( 0) 0)
|
| [13] |
MATTHAIOU M, CHATZIDIAMANTIS N D, SURAWEERA H A, et al. Performance analysis of space-time block codes over generalized-K fading MIMO channels [C]// Proceedings of the 2011 IEEE Swedish Communication Technologies Workshop. Piscataway, NJ: IEEE, 2011: 68-73.
( 0) 0)
|
| [14] |
CHATZIDIAMANTIS N D, KARAGIANNIDIS G K, MICHALOPOULOS D S. On the distribution of the sum of gamma-gamma variates and applications in RF and optical wireless communications [C]// GLOBECOM '09: Proceedings of the 28th IEEE Conference on Global Telecommunications. Piscataway, NJ: IEEE, 2009: 1768-1773.
( 0) 0)
|
| [15] |
GRADSHTEYN I S, RYZHIK I M.
Table of Integrals, Series, and Products[M]. Burlington: USA Academic Press, 2007 .
( 0) 0)
|
| [16] |
MAAREF A, AISSA S. Exact error probability analysis of orthogonal space-time block codes with arbitrary rectangular QAM over MIMO Nakagami-m fading channels [C]// Proceedings of the 2007 IEEE Wireless Communication and Networking Conference. Piscataway, NJ: IEEE, 2007: 768-772.
( 0) 0)
|
| [17] |
Wolfram Research. The Wolfram functions site [EB/OL]. [2016-01-25]. http://functions.wolfram.com/.
( 0) 0)
|
| [18] |
SHARMA B L, ABIODUN R F A. Generating function for generalized function of two variables[J].
Proceedings of the American Mathematical Society, 1974, 46 (1) : 69-72.
doi: 10.1090/S0002-9939-1974-0344536-5 ( 0) 0)
|




