WAN Youhong, born in 1974, Ph. D., professor. Her research interests include complex network theory, network control.
WANG Xiaochu, born in 1991, M. S. candidate. His research interests include complex network theory, information spreading.
随着互联网的兴起,谣言无时不在,无处不在。人们传播谣言的目的具有多样性,包括吸引关注、诽谤他人、制造声势、转移注意或是引起恐慌等[1-3]。信息化的加速使得谣言传播所依赖的媒介(传播工具)得到了飞速的发展,因而使谣言的传播范围更广,传播速度更快。在当今的互联网时代里,谣言的传播会对社会的和谐稳定产生巨大的负面影响[4]。因此,研究谣言的传播机理具有非常重要的现实意义。
Daley和Kendall于20世纪60年代提出了谣言传播的数学模型(简称DK模型)[5],该模型体现了社会中的谣言传播与病毒扩散之间所具有的相似性,在谣言传播的定量研究中被广泛地运用。Zanette等[6-7]首先将复杂网络理论应用于谣言传播的研究,基于在小世界网络上建立的谣言传播模型,得出了谣言传播存在临界值的结论。Moreno等[8]基于不同结构的复杂网络,对谣言传播模型进行了研究,在无标度网络的基础上,对谣言传播的动力学方程组进行了修正,并通过仿真表明网络结构对于谣言传播演化所产生的影响。Isham等[9]基于相互作用的马尔可夫链对谣言传播模型进行了公式化描述,并对谣言分布的最终规模进行了研究。
近年来,由于Moreno等[8]研究的谣言传播模型为谣言传播的研究提供了重要的借鉴,很多学者在此基础上对谣言传播模型进行了改进,使得改进模型更加符合谣言的实际传播演化。Nekovee等[10]将谣言的遗忘率引入Moreno等研究的谣言传播模型,并在同构网络、随机网络和无标度网络下对改进模型的稳态和时变特性进行了分析;Zhao等[11-12]将引入遗忘率的谣言传播模型在LiveJournal社交网络上进行仿真,结果表明遗忘机制在谣言传播过程中起到了十分重要的作用,同时根据对遗忘记忆机制的研究提出了一种新的SIHR谣言传播模型;潘灶烽等[13]在Moreno等研究的谣言传播模型的基础上,研究了具有可变聚类系数的无标度网络上的谣言传播行为。
由于真实社交网络的复杂性,谣言传播模型中不同个体之间状态转化的概率也会随着谣言传播演化过程中各种因素的影响而变化。孙睿等[14]对于谣言传播模型中的谣言传播概率进行了非一致化处理,根据节点度的不同提出了谣言接受度函数,并通过仿真表明不同的谣言接受度函数会导致不同的传播速度和传播阈值。王筱莉等[15]研究了遗忘率随时间变化的谣言传播模型,并在社交网络人人网中进行了数值模拟,结果表明遗忘率对谣言传播的最终规模具有重要影响。
在实际的谣言传播过程中,有时人们相信谣言,是因为其他人也相信。他们会通过自我约束以便自己和大众的意见保持一致。谣言传播与从众压力之间存在着这样的关系:人们会在大众信念面前伪化自己的既有知识,或是压制他们自己的怀疑[16]。将这种从众压力的作用称之为从众效应。从众效应是真实社交网络中普遍存在的,是谣言传播演化过程中不可忽略的影响因素。朱冠桦等[17]研究了社交网络中的从众效应对谣言传播的影响,根据谣言的转发次数和社交网络规模,提出了谣言传播概率的增强幅度函数,对传统的SIR谣言传播模型进行了改进。模型的仿真结果表明谣言的转发人数越多,从众效应的增幅越大,谣言的扩散速度越快,谣言传播者的数量越快达到峰值;同时,扩大社交网络规模可以显著减弱从众效应对谣言传播的影响。
本文考虑到真实社交网络中存在的从众效应,根据人群中不同个体所占比例的变化情况,改进对谣言传播概率以及谣言传播者恢复理性概率的动态化描述,提出考虑从众效应的谣言传播模型,基于不同的网络拓扑,建立对应的谣言传播动力学方程组,利用蒙特卡罗方法模拟谣言在不同拓扑结构网络中的传播演化,并基于真实社交网络进行模拟仿真,观察初始传播个体影响力对谣言传播演化的影响。
1 考虑从众效应的谣言传播模型在从众效应的影响下,人们会强烈地相信某些共同意见。如果相信某个谣言的谣言传播者在人群中的所占比例越大,那么人群中的其他人会在从众效应的影响下,更加容易让自己相信这个谣言,从而成为谣言的传播者;同理,如果不相信谣言,对谣言免疫的理性者在人群中的所占比例越大,那么人群中的其他人会在从众效应的影响下,更加不会去相信这个谣言,从而成为对谣言免疫的理性者。
在以往的谣言传播模型研究中,谣言的传播概率往往作为常量参数代入模型的计算与仿真。然而,在谣言传播的过程中,同一个谣言的可信度是会发生变化的,引起这种变化的因素有很多,包括谣言的时效性、谣言传播个体的自身影响力以及谣言传播的媒介平台等。
在本文中,从众效应对谣言传播概率产生的影响取决于两个因素:一个是谣言本身,这是由谣言的内容所决定的,反映了谣言在初始时刻的可信度,即谣言的初始传播概率;另一个是相信谣言并传播谣言的个体的数量,即谣言传播者在人群中的所占比例。
为了利用动态化描述函数体现这两个因素对于谣言传播概率的影响,首先如果不考虑谣言传播者数量对于谣言传播概率的影响,那么谣言的传播概率即为它的初始传播概率(λ0表示谣言的初始传播概率):
| $ \lambda = {\lambda _0} $ | (1) |
其次考虑谣言传播者数量对谣言传播概率λ产生的影响。本文利用谣言传播者在人群中所占比例的变化来反映谣言传播者数量的变化(s(t)表示在时刻t,谣言传播者在人群中的所占比例)。由于随着谣言传播者数量的增多,从众效应会越发增强,即s(t)的值越大,谣言传播概率λ的值越大,且λ随s(t)增大而增大的幅度也逐渐增加,所以可以用自然指数形式来刻画这种变化关系如下(c表示常数):
| $ \lambda = {e^{c \cdot s\left( t \right)}} $ | (2) |
由于这两种因素对谣言传播概率λ的影响是相互独立的,所以可以将式(1)和式(2)以乘积的形式融合到一个表达式中:
| $ \lambda = {\lambda _0} \cdot {e^{c \cdot s\left( t \right)}} $ | (3) |
注意到s(t)=1时,即人群中所有个体为谣言传播者时,谣言将变得完全可信,所以此时λ=1,即λ0·ec=1,由此可以确定常数c=-ln λ0。
因此本文将谣言传播概率的动态化描述函数定义如下:
| $ \lambda \left( {{\lambda _0},s\left( t \right)} \right) = {\lambda _0} \cdot {{\text{e}}^{ - \ln {\lambda _0} \cdot s\left( t \right)}} $ | (4) |
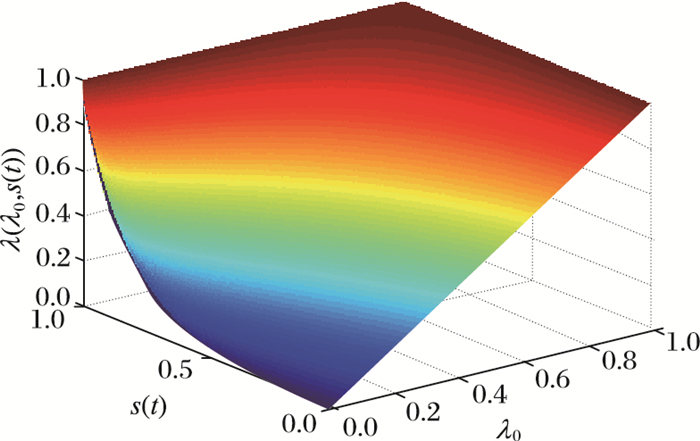
由此可得λ(λ0, s(t))与λ0、s(t)之间的变化关系如图 1所示。
|
图 1 λ(λ0, s(t))与λ0、s(t)之间的变化关系 |
从图 1中可以看出,在谣言的初始传播概率λ0保持不变的情况下,随着t时刻谣言传播者在人群中所占比例s(t)的增大,谣言的传播概率λ(λ0, s(t))的函数值也随之上升;在s(t)保持不变的情况下,随着λ0的增大,λ(λ0, s(t))的函数值也随之上升。
同理,本文定义α(α0, r(t))来表示谣言传播者恢复理性概率的动态化描述函数(α0表示谣言传播者的初始恢复理性概率):
| $ \alpha \left( {{\alpha _0},r\left( t \right)} \right) = {\alpha _0} \cdot {{\text{e}}^{ - \ln {\alpha _0} \cdot r\left( t \right)}} $ | (5) |
在谣言传播者的初始恢复理性概率α0保持不变的情况下,随着t时刻对谣言免疫的理性者在人群中所占的比例r(t)的增大,谣言传播者的恢复理性概率α(α0, r(t))的函数值也随之上升;在r(t)保持不变的情况下,随着α0的增大,α(α0, r(t))的函数值也随之上升。
基于考虑从众效应的谣言传播模型,把总人数为N的人群中的个体分为三类:无知者、传播者和理性者。无知者未曾听说过谣言;传播者相信谣言并传播谣言;理性者听说过谣言但并不相信谣言。当无知者遇到传播者时,无知者会以概率λ(λ0, s(t))变为传播者;当传播者遇到另一个传播者或是理性者时,会以概率α(α0, r(t))变为理性者。
将式(4)和式(5)代入到谣言传播模型中,可以得到均匀网络上考虑从众效应的谣言传播动力学方程组如下:
| $ \frac{{{\text{d}}i\left( t \right)}}{{{\text{d}}t}} = - \bar k \cdot {\lambda _0} \cdot {{\text{e}}^{ - \ln {\lambda _0} \cdot r\left( t \right)}} \cdot i\left( t \right) \cdot s\left( t \right) $ | (6) |
| $ \begin{array}{*{20}{l}} {\frac{{{\text{d}}i\left( t \right)}}{{{\text{d}}t}} = \bar k \cdot {\lambda _0} \cdot {{\text{e}}^{ - \ln {\lambda _0} \cdot r\left( t \right)}} \cdot i\left( t \right) \cdot s\left( t \right) - } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \bar k \cdot {\alpha _0}{{\text{e}}^{ - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot s\left( t \right) \cdot \left[ {s\left( t \right) + r\left( t \right)} \right]} \end{array} $ | (7) |
| $ \frac{{{\text{d}}i\left( t \right)}}{{{\text{d}}t}} = \bar k \cdot {\alpha _0} \cdot {{\text{e}}^{ - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot s\left( t \right) \cdot \left[ {s\left( t \right) + r\left( t \right)} \right] $ | (8) |
其中:
| $ i\left( t \right) + s\left( t \right) + r\left( t \right) = 1 $ | (9) |
同时,可以得到非均匀网络上考虑从众效应的谣言传播动力学方程组如下:
| $ \frac{{{\text{d}}{i_k}\left( t \right)}}{{{\text{d}}t}} = - k{\lambda _0}{i_k}\left( t \right)\sum\limits_{k'} {\frac{{{{\text{e}}^{ - \ln {\lambda _0} \cdot sk'\left( t \right)}}k'P\left( {k'} \right){s_{k'}}\left( t \right)}}{{\left\langle k \right\rangle }}} $ | (10) |
| $ \begin{array}{*{20}{l}} {\frac{{{\text{d}}{s_k}\left( t \right)}}{{{\text{d}}t}} = k{\lambda _0}{i_k}\left( t \right)\sum\limits_{k'} {\frac{{{{\text{e}}^{ - \ln {\lambda _0} \cdot sk'\left( t \right)}}k'P\left( {k'} \right){s_{k'}}\left( t \right)}}{{\left\langle k \right\rangle }}} - } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k{\alpha _0}{s_k}\left( t \right)\sum\limits_{k'} {\frac{{{{\text{e}}^{ - \ln {\alpha _0} \cdot rk'\left( t \right)}}k'P\left( {k'} \right)\left[ {{s_{k'}}\left( t \right) + {r_{k'}}\left( t \right)} \right]}}{{\left\langle k \right\rangle }}} } \end{array} $ | (11) |
| $ \frac{{{\text{d}}{s_k}\left( t \right)}}{{{\text{d}}t}} = k{\alpha _0}{s_k}\left( t \right) \cdot \sum\limits_{k'} {\frac{{{{\text{e}}^{ - \ln {\alpha _0} \cdot rk'\left( t \right)}}k'P\left( {k'} \right)\left[ {{s_{k'}}\left( t \right) + {r_{k'}}\left( t \right)} \right]}}{{\left\langle k \right\rangle }}} $ | (12) |
其中:[k]表示网络的平均度;P(k′)表示节点度为k′的节点概率分布函数;ik(t)、sk(t)和rk(t)分别对应地表示在时刻t,节点度为k的无知者、传播者和理性者在人群中的所占比例。
2 谣言最终传播规模的数值分析在整个谣言的传播演化过程中,谣言传播者在人群中所占的比例先是逐渐增长,达到峰值后开始下降,最终下降至零,意味着谣言的消亡。此时,模型处于稳定状态,人群中只剩下无知者和理性者。本文对谣言的最终传播规模,即理性者在人群中所占比例的稳态值R进行求解,R的等价表达如下:
| $ R = final\left\{ {R\left( t \right)} \right\} = \mathop {\lim }\limits_{t \to \infty } R\left( t \right) = R\left( \infty \right) $ |
用式(8)除以式(6),并将式(9)代入,可以得到:
| $ \begin{array}{*{20}{c}} {\frac{{{\text{d}}r\left( t \right)}}{{{\text{d}}i\left( t \right)}} = \frac{{\bar k \cdot {\alpha _0} \cdot {{\text{e}}^{ - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot s\left( t \right) \cdot \left[ {s\left( t \right) + r\left( t \right)} \right]}}{{ - \bar k \cdot {\lambda _0} \cdot {{\text{e}}^{ - \ln {\lambda _0} \cdot s\left( t \right)}} \cdot i\left( t \right) \cdot r\left( t \right)}} = } \\ {\frac{{{\alpha _0} \cdot {{\text{e}}^{ - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot \left[ {1 - i\left( t \right)} \right]}}{{ - {\lambda _0} \cdot {{\text{e}}^{ - \ln {\lambda _0} \cdot s\left( t \right)}} \cdot i\left( t \right)}} = \frac{{{\alpha _0}}}{{{\lambda _0}}}.} \\ {{{\text{e}}^{\ln {\lambda _0} \cdot s\left( t \right) - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot \frac{{i\left( t \right) - 1}}{{i\left( t \right)}}} \end{array} $ |
上述等式左右两边同时乘以di(t),可以得到:
| $ \begin{array}{*{20}{c}} {{\text{d}}r\left( t \right) = \frac{{{\alpha _0}}}{{{\lambda _0}}} \cdot {{\text{e}}^{\ln {\lambda _0} \cdot s\left( t \right) - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot {\text{d}}r\left( t \right) - \frac{{{\alpha _0}}}{{{\lambda _0}}}.} \\ {{{\text{e}}^{\ln {\lambda _0} \cdot s\left( t \right) - \ln {\alpha _0} \cdot r\left( t \right)}} \cdot \frac{1}{{i\left( t \right)}} \cdot {\text{d}}i\left( t \right)} \end{array} $ |
进一步化简得到:
| $ \frac{{{\lambda _0}}}{{{\alpha _0}}}{{\text{e}}^{\ln {\alpha _0} \cdot r\left( t \right)}}{\text{d}}r\left( t \right) = {{\text{e}}^{\ln {\lambda _0} \cdot s\left( t \right)}}{\text{d}}i\left( t \right) - {{\text{e}}^{\ln {\lambda _0} \cdot s\left( t \right)}}\frac{{{\text{d}}i\left( t \right)}}{{i\left( t \right)}} $ | (13) |
再将式(9)代入,并对等式两边进行化简,可以得到:
| $ \begin{array}{*{20}{l}} {\frac{{{\lambda _0}}}{{{\alpha _0}}}{{\text{e}}^{\left( {^{\ln {\alpha _0} + \ln {\lambda _0}}} \right) \cdot r\left( t \right)}}{\text{d}}r\left( t \right) = {{\text{e}}^{\ln {\lambda _0} \cdot \left[ {1 - i\left( t \right)} \right]}}{\text{d}}i\left( t \right) - } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\text{e}}^{\ln {\lambda _0} \cdot \left[ {1 - i\left( t \right)} \right]}}\frac{{{\text{d}}i\left( t \right)}}{{i\left( t \right)}}} \end{array} $ | (14) |
在式(14)中,等式的左右两边可以分别对r(t)和i(t)进行求积运算,其中
| $ \frac{{{\lambda _0}\left( {{{\text{e}}^{\left( {^{\ln {\alpha _0} + \ln {\lambda _0}}} \right)R}} - 1} \right)}}{{{\alpha _0}\left( {\ln {\alpha _0} + \ln {\lambda _0}} \right)}} = \frac{{1 - {{\text{e}}^{\left( {\ln {\lambda _0}} \right)R}}}}{{\ln {\lambda _0}}} + \int_0^R {\frac{{{{\text{e}}^{\left( {\ln {\lambda _0}} \right)x}}}}{{1 - x}}{\text{d}}x} $ | (15) |
其中:
| $ \begin{array}{*{20}{l}} {\int_0^R {\frac{{{{\text{e}}^{\left( {\ln {\lambda _0}} \right)x}}}}{{1 - x}}{\text{d}}x} \approx {{\text{e}}^{\left( {\ln {\lambda _0}} \right)}} \cdot \left[ {{\text{ - }}\ln \left( {1 - R} \right) - R \cdot \ln {\lambda _0} + \left( {1/4} \right)} \right. \cdot } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {2R - {R^2}} \right) \cdot {{\left( {\ln {\lambda _0}} \right)}^2} - \left( {1/18} \right) \cdot \left( {{R^3} - 3{R^2} + 3R} \right) \cdot } \\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {\ln {\lambda _0}} \right)}^3}} \right] = simp\left( R \right)} \end{array} $ |
因此,将simp(R)代入式(15)可得:
| $ \frac{{{\lambda _0}\left( {{{\text{e}}^{\left( {^{\ln {\alpha _0} + \ln {\lambda _0}}} \right)R}} - 1} \right)}}{{{\alpha _0}\left( {\ln {\alpha _0} + \ln {\lambda _0}} \right)}} - \frac{{\left( {1 - {{\text{e}}^{\left( {\ln {\lambda _0}} \right)R}}} \right)}}{{\ln {\lambda _0}}} - simp\left( R \right) = 0 $ |
基于上式,不妨定义函数f(x)如下:
| $ f\left( x \right) = \frac{{{\lambda _0}\left( {{{\text{e}}^{\left( {^{\ln {\alpha _0} + \ln {\lambda _0}}} \right)x}} - 1} \right)}}{{{\alpha _0}\left( {\ln {\alpha _0} + \ln {\lambda _0}} \right)}} - \frac{{\left( {1 - {{\text{e}}^{\left( {\ln {\lambda _0}} \right)x}}} \right)}}{{\ln {\lambda _0}}} - simp\left( x \right) $ |
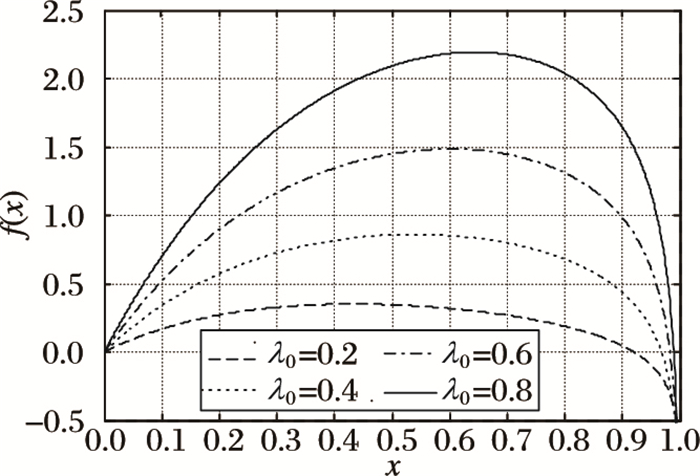
在直角坐标系中,当λ0分别取值0.2、0.4、0.6和0.8,且α0=0.1时,可以得到f(x)在区间[0, 1]内的函数图像。
从图 2中可以看出,存在不为零的x*,使得函数f(x)=0成立。此时,x*即为理性者在人群中所占比例的稳态值R。从图 2中可以发现,当谣言的初始传播概率λ0逐渐增大时,使得函数f(x)=0成立的x*的值逐渐增大,即稳态值R逐渐增大。因此,谣言的最终传播规模随着谣言的初始传播概率λ0的增大而增大。
|
图 2 f(x)在区间[0, 1]内的函数图像 |
为了体现从众效应对谣言传播演化产生的影响,本文通过仿真实验将考虑从众效应的谣言传播模型与Moreno等研究的谣言传播模型进行对比。
本文首先将两种谣言传播模型在均匀网络上进行仿真,所选取的相同的仿真参数为:网络总节点数N=1000,网络的平均度
|
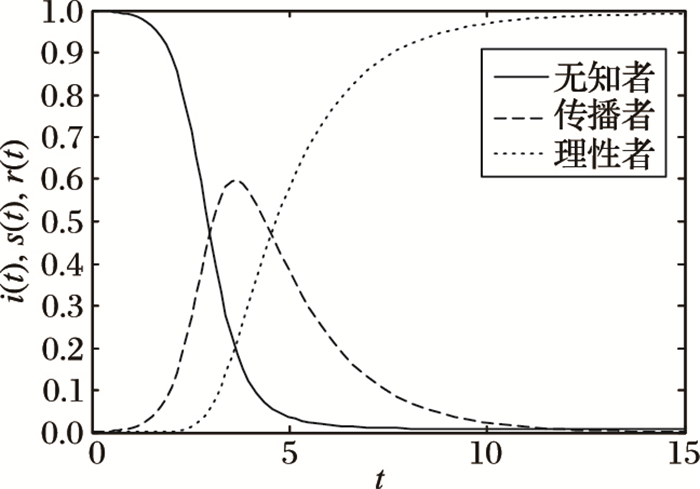
图 3 Moreno等研究的谣言传播模型(均匀网络) |
|
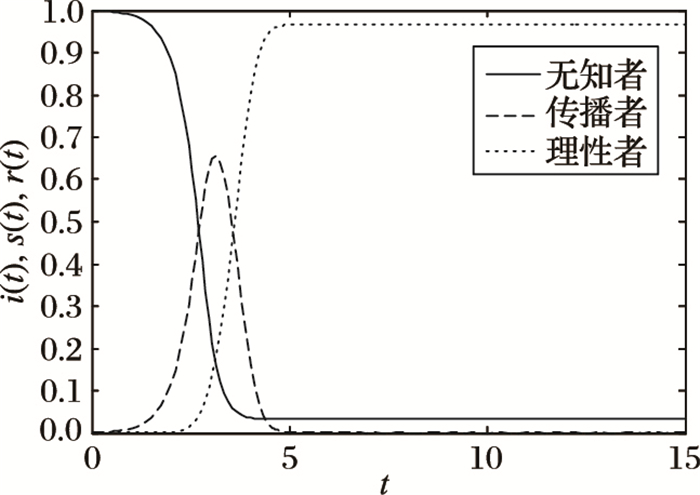
图 4 考虑从众效应的谣言传播模型(均匀网络) |
从图 3中可以看出,在Moreno等研究的谣言传播模型中,谣言的传播者在人群中的所占比例在t接近于1.5时开始以较快的速度增长,谣言在t约为4时发生最大面积传播,s(t)的峰值约为0.6。在t约为11时,三类个体在人群中所占的比例的值趋于稳定。
从图 4中可以看出,在考虑从众效应的谣言传播模型中,谣言的传播者在人群中的所占比例在t接近于1时开始以较快的速度增长,谣言在t约为3.5时发生最大面积传播,s(t)的峰值约为0.65。在t约为5时,三类个体在人群中所占的比例的值趋于稳定。
从图 4与图 3的比较中可以发现,在考虑从众效应的谣言传播模型中,谣言发生最大面积传播所需要的时间更短,s(t)的峰值更大。在t约为5时,人群中三类个体的密度值就已经趋于稳定,小于Moreno等研究的谣言传播模型中与之相对应的仿真结果。因此,从众效应加快了谣言的传播演化速度。
为了体现在不同的网络拓扑结构下,从众效应对谣言传播演化产生的影响,本文分别基于考虑从众效应的谣言传播模型和Moreno等研究的谣言传播模型,利用蒙特卡罗方法在小世界网络和无标度网络上模拟谣言的传播演化。
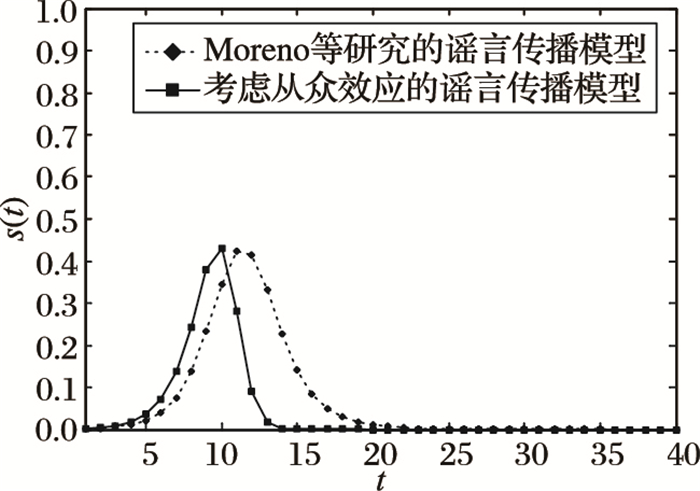
基于WS小世界网络[18]和BA无标度网络[19]的生成规则,本文分别构造了网络总节点数为1000,网络平均度为6的小世界网络和无标度网络,用来作为模拟谣言传播演化的网络底图。在进行蒙特卡罗模拟仿真时,为了有效消除仿真结果可能具有的不确定性,本文选取重复仿真实验次数n=100。图 5和图 6分别是谣言在小世界网络和无标度网络中传播时,谣言传播者在人群中所占比例随时间的变化,所得到的实验结果均是按照上述模型中提到的谣言传播规则独立进行了100次重复仿真实验后所得到的平均结果。
|
图 5 谣言传播者在人群中所占比例随时间的变化(小世界网络) |
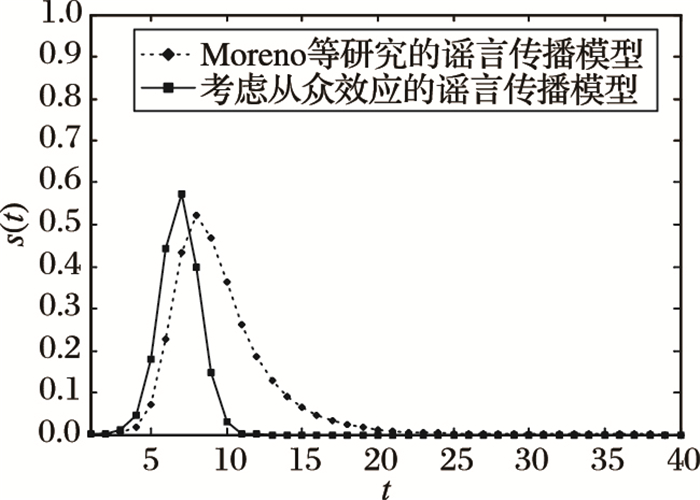
|
图 6 谣言传播者在人群中所占比例随时间的变化(无标度网络) |
从图 5中可以看出,谣言在小世界网络中传播时,从众效应使得谣言传播者在人群中所占比例达到峰值的时间缩短,并使得谣言消亡的时间进一步缩短,但是在两种模型中,s(t)的峰值并没有发生明显的变化。从图 6中可以看出,谣言在无标度网络中传播时,从众效应同样使得谣言传播者在人群中所占比例达到峰值的时间缩短,而且在考虑从众效应的谣言传播模型中,s(t)的峰值有较为明显的增加。
结合图 5和图 6可以发现,对于不同的网络拓扑结构,从众效应对谣言传播演化产生的影响具有差异性。谣言在具有幂律度分布的无标度网络中传播时,从众效应不仅加速了谣言的传播演化,而且使得谣言传播者在人群中所占比例的峰值增加,使谣言的负面影响加深。
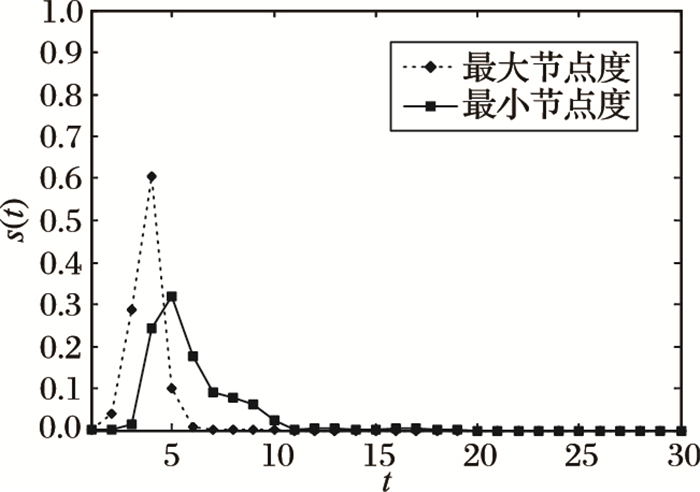
为了体现谣言从不同影响力的节点上传播时从众效为了体现谣言从不同影响力的节点上传播时从众效应所产生影响的区别, 本文将考虑从众效应的谣言传播模型基于真实的社交网络模拟仿真, 并选择不同节点度的节点作为谣言的初始传播节点, 观察谣言传播者在人群中所占比例随时间的变化关系。使用真实的Facebook用户数据集作为底图, 总节点数为6575, 节点的最大节点度为628, 节点的最小节点度为1, 图 7是初始传播节点分别选取最大度节点和最小度节点时, 谣言传播者在人群中所占比例的变化情况, 所得结果为独立进行了100次重复仿真实验后的平均实验结果。
|
图 7 初始传播节点度不同时谣言传播者的变化情况 |
从图 7中可以看出:当初始传播节点的节点度最大时,s(t)在t约为4时达到峰值,其峰值约为0.6;而当初始传播节点的节点度最小时,s(t)在t约为5时达到峰值,其峰值约为0.25。由此可以发现,在考虑从众效应的谣言传播模型中,谣言的初始传播个体影响力越大,谣言传播的速度越快,且谣言传播者在人群中所占比例所对应的峰值越大。
4 结语本文考虑到真实社交网络中存在的从众效应,研究了从众效应对于谣言传播演化所具有的影响,在Moreno等研究的谣言传播模型的基础上,改进了对谣言传播概率以及谣言传播者恢复理性概率的动态化描述,提出了考虑从众效应的谣言传播模型。数值分析结果表明了谣言的最终传播规模与谣言的初始传播概率之间的关系。改进模型的Matlab仿真结果表明从众效应对于谣言的传播演化具有加速作用。本文利用蒙特卡罗方法模拟了谣言在小世界网络和无标度网络中的传播演化,结果表明在从众效应的影响下,谣言在无标度网络中传播的速度更快,扩散的程度更深。此外,谣言传播的速度和谣言传播者在人群中所占比例的峰值随着谣言初始传播个体的影响力的增大而增大。
在实际的谣言传播演化中,影响谣言传播概率的因素还有很多,如何将这些因素通过数学形式在谣言传播概率的动态化函数中体现值得进一步研究。
| [1] |
KOSTKA J, OSWALD Y A, WATTENHOFER R. Word of mouth: rumor dissemination in social networks [M]// Structural Information and Communication Complexity, LNCS 5058. Berlin: Springer, 2008: 185-196.
( 0) 0)
|
| [2] |
ZHANG Z L, ZHANG Z Q. An interplay model for rumour spreading and emergency development[J].
Physica A: Statistical Mechanics and its Applications, 2009, 388 (19) : 4159-4166.
doi: 10.1016/j.physa.2009.06.020 ( 0) 0)
|
| [3] |
KOSFELD M. Rumours and markets[J].
Journal of Mathematical Economics, 2005, 41 (6) : 646-664.
doi: 10.1016/j.jmateco.2004.05.001 ( 0) 0)
|
| [4] |
BROOKS B. Rumour propagation on social networks as a function of diversity [M]// Advanced Dynamic Modeling of Economic and Social Systems. Berlin: Springer, 2013, 448: 49-60.
( 0) 0)
|
| [5] |
DALEY D J, KENDALL D G. Epidemics and rumours[J].
Nature, 1964, 204 (4963) : 1118.
doi: 10.1038/2041118a0 ( 0) 0)
|
| [6] |
ZANETTE D H. Critical behavior of propagation on small-world networks [EB/OL]. [2015-10-26]. https://www.researchgate.net/publication/11620300_Zanette_D_Critical_behavior_of_propagation_on_small-world_networks_Phys_Rev_E_644_050901.
( 0) 0)
|
| [7] |
ZANETTE D H. Dynamics of rumor propagation on small-world networks [EB/OL]. [2015-10-26]. http://www.arteuna.com/talleres/lab/ediciones/libreria/rumor%20propagation.pdf.
( 0) 0)
|
| [8] |
MORENO Y, NEKOVEE M, PACHECO A F. Dynamics of rumor spreading in complex networks [EB/OL]. [2015-11-05]. http://www.uvm.edu/~pdodds/files/papers/others/2003/moreno2003u.pdf.
( 0) 0)
|
| [9] |
ISHAM V, HARDEN S, NEKOVEE M. Stochastic epidemics and rumours on finite random networks[J].
Physica A: Statistical Mechanics and its Applications, 2010, 389 (3) : 561-576.
doi: 10.1016/j.physa.2009.10.001 ( 0) 0)
|
| [10] |
NEKOVEE M, MORENO Y, BIANCONI G, et al. Theory of rumour spreading in complex social networks[J].
Physica A: Statistical Mechanics and its Applications, 2007, 374 (1) : 457-470.
doi: 10.1016/j.physa.2006.07.017 ( 0) 0)
|
| [11] |
ZHAO L J, WANG Q, CHENG J, et al. Rumor spreading model with consideration of forgetting mechanism: a case of online blogging LiveJournal[J].
Physica A: Statistical Mechanics and its Applications, 2011, 390 (13) : 2619-2625.
doi: 10.1016/j.physa.2011.03.010 ( 0) 0)
|
| [12] |
ZHAO L, WANG J, CHEN Y, et al. SIHR rumor spreading model in social networks[J].
Physica A: Statistical Mechanics and its Applications, 2012, 391 (7) : 2444-2453.
doi: 10.1016/j.physa.2011.12.008 ( 0) 0)
|
| [13] |
潘灶烽, 汪小帆, 李翔. 可变聚类系数无标度网络上的谣言传播仿真研究[J].
系统仿真学报, 2006, 18 (8) : 2346-2348.
( PAN Z F, WANG X F, LI X. Simulation investigation on rumor spreading on scale-free network with tunable clustering[J].
Journal of System Simulation, 2006, 18 (8) : 2346-2348.
) ( 0) 0)
|
| [14] |
孙睿, 罗万伯. 具有非一致传播率的无标度网络谣言传播模型[J].
复杂系统与复杂性科学, 2014, 11 (3) : 6-11.
( SUN R, LUO W B. Rumor propagation model for scale-free network with non-uniform propagation rates[J].
Complex Systems and Complexity Science, 2014, 11 (3) : 6-11.
) ( 0) 0)
|
| [15] |
王筱莉, 赵来军, 谢婉林. 无标度网络中遗忘率变化的谣言传播模型研究[J].
系统工程理论实践, 2015, 35 (2) : 458-465.
( WANG X L, ZHAO L J, XIE W L. Rumor spreading model with variable forgetting rate in scale-free network[J].
Systems Engineering Theory and Practice, 2015, 35 (2) : 458-465.
) ( 0) 0)
|
| [16] |
SUNSTEIN C R.
On Rumors: How Falsehoods Spread, Why We Believe Them, and What Can Be Done[M]. New York: Farrar, Straus and Giroux, 2014 : 28 -32.
( 0) 0)
|
| [17] |
朱冠桦, 蒋国平, 夏玲玲. 社交网络上从众现象对谣言传播影响的研究[J].
计算机科学, 2016, 43 (2) : 135-139.
( ZHU G H, JIANG G P, XIA L L. Rumor spreading model considering conformity phenomena in complex social networks[J].
Computer Science, 2016, 43 (2) : 135-139.
) ( 0) 0)
|
| [18] |
WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J].
Nature, 1998, 393 (6684) : 440-442.
doi: 10.1038/30918 ( 0) 0)
|
| [19] |
BARABASI A L, ALBERT R. Emergence of scaling in random networks[J].
Science, 1999, 286 (5439) : 509-512.
doi: 10.1126/science.286.5439.509 ( 0) 0)
|




