2. 宝鸡市高新技术研究所, 陕西 宝鸡 721000
2. Baoji New High Tech Research Institute, Baoji Shaanxi 721000, China
随着人类对太空探索和应用的深入,空间机器人以其质量轻、手臂长和负载大等优点,发挥着越来越重要的作用[1-2]。将空间机器人设计为柔性轻质细长杆件,既可减小发射质量,又可节约发射成本。为获得更好的控制精度和性能,需考虑空间机器人杆件的柔性。同时,从节省燃料、增加在轨寿命的角度考虑,对载体位置和姿态均不受控的自由漂浮柔性空间机器人(Free-Floating Flexible Space Robot,FFFSR)的研究非常必要[3-4]。
由于包含振动模态的柔性机器人系统动力学方程阶数较高,且柔性振动频率一般比其刚性运动频率要高得多,大多数方案将刚性运动控制和柔性振动抑制在同一时间尺度上进行叠加,势必会影响刚性运动控制系统的鲁棒性和稳定性。文献[5]建立了一类高阶柔性机械臂的奇异摄动模型并进行了仿真实验,文献[6]则针对基体振动的机械臂系统运用奇异摄动法建立动力学方程。上述研究主要将奇异摄动法应用于柔性地面机器人,对于基座与臂杆存在动力学耦合关系的空间机器人研究较少。
在实际工程应用中,FFFSR系统必须具备在不确定条件下仍能实现精确跟踪控制和柔性振动抑制的能力[7-9]。对于低速运动的空间机器人,关节角速度测量难度大,易引入噪声干扰,对系统控制性能造成很大影响。如何设计角速度观测器以及利用角度信息设计控制器对工程应用的价值显得尤为重要。文献[10]提出一种位置反馈控制策略,但观测器的设计依赖精确动力学模型;文献[11]提出一种鲁棒轨迹跟踪控制策略,并在假设惯性矩阵特征值变化的情况下设计滑模观测器;文献[12]利用神经网络法设计一种输出反馈控制器,无需精确的动力学模型;文献[13]提出一种基于神经网络的滑模自适应控制策略,但仅有隐含层到输出层的权值矩阵可调,观测器的设计仍需要精确的惯性逆矩阵。值得注意的是,为避免由初始误差引起的冲击力矩的影响,且受到发射装置质量、体积以及为执行器供能的蓄电池电压等因素的约束,系统的控制力矩将限制在一定范围内[14-15]。当力矩超出限值时将表现饱和特性,导致系统控制性能下降,甚至失去稳定性。因此,在设计控制器时必须考虑关节执行器输出力矩受限的情况。
针对柔性振动的主动抑制问题,文献[16]采用应变率反馈(Strain Rate Feedback,SRF)控制有效抑制了3PRR并联柔性机械臂的振动;文献[17]采用线性观测器对柔性模态进行估计,并结合线性二次调节器(Linear Quadratic Regulator,LQR)法,对柔性振动进行抑制。上述方案虽能抑制柔性振动,但均未考虑振动抑制的外界扰动,不符合工程实际。扩张状态观测器(Extended State Observer,ESO)可将系统包含的非线性动态、系统不确定性以及外部干扰等当作可观测的扩张状态,无需具体的扰动模型,是一种通用的扰动观测器[18]。
针对上述问题,本文采用奇异摄动法将FFFSR系统降阶分解为两种时间尺度的奇异摄动模型,避免了在同一时间尺度下关节轨迹跟踪和柔性振动抑制方案简单叠加的问题;提出一种基于速度观测器的模糊径向基函数(Radial Basis Function,RBF)神经网络关节轨迹跟踪策略,不仅对关节角速度进行估计,同时补偿系统的未知非线性部分;同时,利用双曲正切函数对控制力矩的范围进行有效限制;采用ESO对不易测量的柔性模态坐标导数和不确定扰动进行估计,并结合最优控制理论,抑制柔性振动。所提出的控制策略仅依赖关节角度信息,无需系统精确的动力学模型,也无需求解惯性逆矩阵;可对权值矩阵在线自适应调节,免除离线学习阶段,满足实时性要求。通过仿真实验验证了所设计的组合控制器的有效性。
1 系统动力学建模与奇异摄动分解 1.1 动力学建模不失一般性,考虑在平面内运动的FFFSR系统的结构如图 1所示[17]。忽略微重力梯度,采用假设模态法对柔性振动进行描述,并由拉格朗日第二类方程和动量守恒原理可得,基座位姿不受控的FFFSR欠驱动形式的系统动力学方程为:
| (1) |
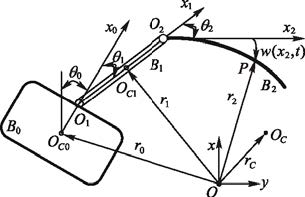
|
图 1 自由漂浮柔性空间机器人系统 |
其中:θ=[θ0,θ1,θ2]T,η=[η1,η2]T。D(θ,η)为5×5的对称正定质量矩阵;$\mathbf{h}\left( \mathbf{\theta },\mathbf{\dot{\theta }},\mathbf{\eta },\mathbf{\dot{\eta }} \right){{\left( {{{\mathbf{\dot{\theta }}}}^{\text{T}}}\text{ }{{{\mathbf{\dot{\eta }}}}^{\text{T}}} \right)}^{\text{T}}}$为包含离心力、科氏力的5阶列向量;K=diag(k11,k22)为柔性杆的刚度矩阵;τ=[τ0,τ1,τ2]T为基座姿态和机械臂两个关节的控制输入力矩组成的3阶列向量,由于系统处于自由漂浮状态,故基座姿态不受控,即τ0=0。
性质1 $\mathbf{\dot{D}}\left( \mathbf{\theta },\mathbf{\eta } \right)-2\mathbf{h}\left( \mathbf{\theta },\mathbf{\dot{\theta }},\mathbf{\eta },\mathbf{\dot{\eta }} \right)$为斜对称阵,即:
| ${{\mathbf{x}}^{\text{T}}}\left( \mathbf{\dot{D}}\left( \mathbf{\theta },\mathbf{\eta } \right)-2\mathbf{h}\left( \mathbf{\theta },\mathbf{\dot{\theta }},\mathbf{\eta },\mathbf{\dot{\eta }} \right) \right)\mathbf{x}\text{=}0$ | (2) |
本节利用奇异摄动法将FFFSR系统降阶分解为两种时间尺度下的关节轨迹跟踪控制慢变子系统和柔性振动抑制快变子系统。
将式(1)写成分块矩阵形式:
| (3) |
其中:Drr和hrr为3×3的子矩阵;Dff和hff为2×2的子矩阵;Drf=DTfr和hrf=hTfr为3×2的子矩阵。定义正定质量矩阵D(θ,η)的逆为:
| $\mathbf{N}=\left[ \begin{matrix} {{\mathbf{N}}_{11}} & {{\mathbf{N}}_{12}} \\ {{\mathbf{N}}_{21}} & {{\mathbf{N}}_{22}} \\ \end{matrix} \right]={{\left[ \begin{matrix} {{\mathbf{D}}_{rr}} & {{\mathbf{D}}_{rf}} \\ {{\mathbf{D}}_{fr}} & {{\mathbf{D}}_{ff}} \\ \end{matrix} \right]}^{-1}}$ | (4) |
将式(4)左乘式(3),并设k=min(k11,k22),定义ε2=1/k为比例因子,引入新的变量ε2ξ=η,=ε2K,重新整理各项,可得:
| $\begin{align} & \mathbf{\ddot{\theta }}\text{=}-{{\mathbf{N}}_{11}}\left( {{\mathbf{h}}_{rr}}\mathbf{\dot{\theta }} \right.+\left. {{\mathbf{h}}_{rf}}{{\varepsilon }^{2}}\mathbf{\dot{\xi }} \right)-{{\mathbf{N}}_{12}}\left( {{\mathbf{h}}_{fr}}\mathbf{\dot{\theta }} \right.+{{\mathbf{h}}_{ff}}\left. {{\varepsilon }^{2}}\mathbf{\dot{\xi }} \right)- \\ & {{\mathbf{N}}_{12}}\mathbf{\tilde{K}\xi }+{{\mathbf{N}}_{11}}\mathbf{\tau } \end{align}$ | (5a) |
| $\begin{align} & {{\varepsilon }^{2}}\mathbf{\ddot{\xi }}\text{=}-{{\mathbf{N}}_{21}}\left( {{\mathbf{h}}_{rr}}\mathbf{\dot{\theta }} \right.+\left. {{\mathbf{h}}_{rf}}{{\varepsilon }^{2}}\mathbf{\dot{\xi }} \right)-{{\mathbf{N}}_{22}}\left( {{\mathbf{h}}_{fr}}\mathbf{\dot{\theta }} \right.+{{\mathbf{h}}_{ff}}\left. {{\varepsilon }^{2}}\mathbf{\dot{\xi }} \right)- \\ & {{\mathbf{N}}_{22}}\mathbf{\tilde{K}\xi }+{{\mathbf{N}}_{21}}\mathbf{\tau } \end{align}$ | (5b) |
| $\mathbf{\tau }\text{=}{{\mathbf{\tau }}_{s}}\left( \mathbf{\theta } \right)+{{\mathbf{\tau }}_{f}}\left( \mathbf{\eta } \right)$ | (6) |
系统的控制目的是设计控制输入τ使得机械臂关节能稳定跟踪期望轨迹并柔性振动得到抑制,因此控制输入τ可分解为两个部分:
| $\mathbf{\bar{\xi }}\text{=}{{\mathbf{\tilde{K}}}^{-1}}\mathbf{N}_{22s}^{-1}\left[ -{{\mathbf{N}}_{21s}}{{\mathbf{h}}_{rrs}}\mathbf{\dot{\theta }}-{{\mathbf{N}}_{22s}}{{\mathbf{h}}_{frs}}\mathbf{\dot{\theta }}+{{\mathbf{N}}_{21s}}{{\mathbf{\tau }}_{s}} \right]$ | (7) |
其中:τs(θ)为慢变跟踪部分;τf(η)为快变抑制部分。由式(5)~(6)可知,恰当地选择控制输入τ可满足轨迹跟踪的预期效果,但并不能保证柔性振动得到抑制,故采用奇异摄动法分解轨迹跟踪和振动抑制子系统分别控制。
令ε=0,并代入式(6)可得:
| ${{\mathbf{D}}_{rrs}}\mathbf{\ddot{\theta }}+{{\mathbf{h}}_{rrs}}\mathbf{\dot{\theta }}={{\mathbf{\tau }}_{s}}$ | (8) |
其中:有下标的向量表示其位于慢变子系统中。将式(8)代入式(5),可得柔性空间机器人慢变子系统表达式为:
| ${{D}_{rrs}}\ddot{\theta }+{{h}_{rrs}}\dot{\theta }=\tau $ | (9) |
为得到系统的快变子系统,选择新的状态变量${{\mathbf{\zeta }}_{1}}\text{=}\mathbf{\xi }-\mathbf{\bar{\xi }},{{\mathbf{\zeta }}_{2}}\text{=}\varepsilon \mathbf{\dot{\xi }}$,式(6)改写为:
| $\begin{align} & \varepsilon {{{\mathbf{\dot{\zeta }}}}_{2}}\text{=}-{{\mathbf{N}}_{21}}\left( {{\mathbf{h}}_{rr}}\mathbf{\dot{\theta }}+{{\mathbf{h}}_{rf}}\varepsilon {{\mathbf{\zeta }}_{2}} \right)-{{\mathbf{N}}_{22}}\left( {{\mathbf{h}}_{fr}}\mathbf{\dot{\theta }}+{{\mathbf{h}}_{ff}}\varepsilon {{\mathbf{\zeta }}_{2}} \right)- \\ & \text{ }{{\mathbf{N}}_{22}}\mathbf{\tilde{K}}\left( {{\mathbf{\zeta }}_{1}}+\mathbf{\bar{\xi }} \right)+{{\mathbf{N}}_{21}}\mathbf{\tau } \end{align}$ | (10) |
引入新的时间尺度σ=t/ε,令ε=0,可得到快变子系统为:
| $\left\{ \begin{align} & \frac{\text{d}{{\mathbf{\zeta }}_{1}}}{\text{d}\sigma }\text{=}{{\mathbf{\zeta }}_{2}} \\ & \frac{\text{d}{{\mathbf{\zeta }}_{2}}}{\text{d}\sigma }\text{=}-{{\mathbf{N}}_{22}}\mathbf{\tilde{K}}{{\mathbf{\zeta }}_{1}}+{{\mathbf{N}}_{21}}{{\mathbf{\tau }}_{f}} \\ \end{align} \right.$ | (11) |
在不同的时间尺度下,慢、快变子系统的控制力矩τs和τf可分别进行设计。最终得到能稳定跟踪期望轨迹并有效抑制柔性振动的力矩τ。
2 自适应模糊神经网络控制器设计在实际控制系统中,当期望控制力矩超出可执行范围时将表现出饱和特性,严重影响系统的控制性能。为避免执行器出现饱和状态,利用双曲函数τs=τmaxtanh(u/τmax)将控制力矩限制在给定范围内,设超出力矩执行范围的部分为δ(δ=u-τs)。可将慢变子系统的动力学方程表示为:
| ${{\mathbf{D}}_{r}}\left( \mathbf{\theta } \right)\mathbf{\ddot{\theta }}+{{\mathbf{h}}_{r}}\left( \mathbf{\theta },\mathbf{\dot{\theta }} \right)\mathbf{\dot{\theta }}+{{\mathbf{\tau }}_{d}}={{\mathbf{\tau }}_{s}}=\mathbf{u}-\mathbf{\delta }$ | (12) |
其中:${{\mathbf{D}}_{r}}\left( \mathbf{\theta } \right)\text{=}{{\mathbf{D}}_{rrs}}\left( \mathbf{\theta } \right),{{\mathbf{h}}_{r}}\left( \mathbf{\theta },\mathbf{\dot{\theta }} \right)={{\mathbf{h}}_{rrs}}\left( \mathbf{\theta },\mathbf{\dot{\theta }} \right)$;τd为系统的有界不确定部分,包括参数不确定、建模误差、摩擦力和外部扰动等。
定义状态变量x1=θ,${{\mathbf{x}}_{2}}=\mathbf{\dot{\theta }}$,将式(12)对应的状态空间方程描述为:
| $\left\{ \begin{align} & {{{\mathbf{\dot{x}}}}_{1}}={{\mathbf{x}}_{2}} \\ & {{{\mathbf{\dot{x}}}}_{2}}={{\mathbf{h}}_{o}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}},{{{\mathbf{\hat{x}}}}_{2}} \right)+\mathbf{u} \\ \end{align} \right.$ | (13) |
为使FFFSR系统稳定跟踪期望轨迹,需要设计观测器来获得关节角速度信号,并利用模糊RBF神经网络逼近观测器和控制器的未知部分。慢变子系统控制结构如图 2所示。
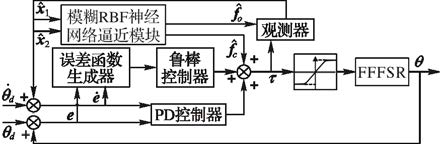
|
图 2 慢变子系统控制 |
在运动过程中,关节转动角速度不易测量且易引入噪声干扰,需要估计。本节设计模糊神经网络自适应观测器对关节的角度和角速度进行估计。将模糊系统推理能力与RBF神经网络逼近能力相结合,构成模糊RBF神经网络,逼近任意非线性函数[19]。令${\mathbf{\hat{\theta }}}$和${\mathbf{\dot{\hat{\theta }}}}$分别为关节角度和角速度的估计值;${\mathbf{\tilde{\theta }}}$和${\mathbf{\dot{\tilde{\theta }}}}$分别为关节角度和角速度的估计误差。即:
| $\left\{ \begin{align} & \mathbf{\tilde{\theta }}\text{=}\mathbf{\theta }-\mathbf{\hat{\theta }} \\ & \mathbf{\dot{\tilde{\theta }}}\text{=}\mathbf{\dot{\theta }}-\mathbf{\dot{\hat{\theta }}} \\ \end{align} \right.$ | (14) |
考虑到系统是未知非线性系统的,可将状态空间方程式(13)改写为:
| $\left\{ \begin{align} & {{{\mathbf{\dot{x}}}}_{1}}={{\mathbf{x}}_{2}} \\ & {{{\mathbf{\dot{x}}}}_{2}}={{\mathbf{h}}_{o}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}},{{{\mathbf{\hat{x}}}}_{2}} \right)+\mathbf{u} \\ \end{align} \right.$ | (15) |
其中:ho=(I-Dr(x1))-hr(x1,x2)x2-τd-δ,ho表示观测器中的未知不确定部分,利用模糊RBF神经网络对未知不确定函数${{\mathbf{h}}_{o}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}},{{{\mathbf{\hat{x}}}}_{2}} \right)$进行学习。根据式(15),将最优逼近表示为:
| ${{\mathbf{h}}_{o}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}},{{{\mathbf{\hat{x}}}}_{2}} \right)\text{=}{{\mathbf{f}}_{o}}\left( \mathbf{x},{{w}^{*}},{{c}^{*}},\mathbf{W}_{o}^{*} \right)=\mathbf{W}_{o}^{*\text{T}}\phi \left( \mathbf{x},{{w}^{*}},{{c}^{*}} \right)+{{\mathbf{\varepsilon }}_{o}}\left( \mathbf{x} \right)$ | (16) |
其中:x=(x1,x2),εo(x)表示逼近误差,并满足$\left\| {{\mathbf{\varepsilon }}_{o}}\left( \mathbf{x} \right) \right\|\le {{\mathbf{\varepsilon }}_{oM}},\left\| \mathbf{W}_{o}^{*} \right\|\le {{\mathbf{W}}_{oM}},\left\| {{\mathbf{w}}^{*}} \right\|\le {{\mathbf{w}}_{M}}和\left\| {{c}^{*}} \right\|\le {{c}_{M}}$。
观测器的估计输出可表示为:
| ${{\mathbf{\hat{f}}}_{o}}\left( \mathbf{\hat{x}},\hat{w},\hat{c},{{{\mathbf{\hat{W}}}}_{o}} \right)=\mathbf{\hat{W}}_{o}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)$ | (17) |
其中:${{\mathbf{\hat{W}}}_{o}}$为观测器的估计权值矩阵,$\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)$是隐含层的输出。设计如下形式的模糊RBF神经网络状态观测器:
| $\left\{ \begin{align} & {{{\mathbf{\dot{\hat{z}}}}}_{1}}={{{\mathbf{\hat{x}}}}_{2}}+{{k}_{2}}{{{\mathbf{\tilde{x}}}}_{1}} \\ & {{{\mathbf{\dot{\hat{z}}}}}_{2}}=\mathbf{\hat{W}}_{o}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)+\mathbf{u}+\left( \mathbf{K}+{{k}_{1}}{{k}_{2}}\mathbf{I} \right){{{\mathbf{\tilde{x}}}}_{1}} \\ \end{align} \right.$ | (18) |
其中:${{\mathbf{\tilde{x}}}_{1}}={{\mathbf{x}}_{1}}-{{\mathbf{\hat{x}}}_{1}},{{\mathbf{\tilde{x}}}_{2}}={{\mathbf{x}}_{2}}-{{\mathbf{\hat{x}}}_{2}},\mathbf{K}={{\mathbf{K}}^{\text{T}}}$为正定阵,k1>0,k2>0。定义系统状态空间(15)中x1、x2的估计值为:
| $\left\{ \begin{align} & {{{\mathbf{\hat{x}}}}_{1}}={{{\mathbf{\hat{z}}}}_{1}} \\ & {{{\mathbf{\hat{x}}}}_{2}}={{{\mathbf{\hat{z}}}}_{2}}+{{k}_{1}}{{{\mathbf{\tilde{x}}}}_{1}} \\ \end{align} \right.$ | (19) |
将式(18)代入式(19),并与式(15)相减,可得动态观测误差为:
| $\left\{ \begin{align} & {{{\mathbf{\dot{\tilde{x}}}}}_{1}}={{{\mathbf{\tilde{x}}}}_{2}}-{{k}_{2}}{{{\mathbf{\tilde{x}}}}_{1}} \\ & {{{\mathbf{\dot{\tilde{x}}}}}_{2}}=\mathbf{W}_{o}^{*\text{T}}\phi \left( \mathbf{x},{{w}^{*}},{{c}^{*}} \right)-\mathbf{\hat{W}}_{o}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)+ \\ & {{\mathbf{\varepsilon }}_{o}}\left( \mathbf{x} \right)-\mathbf{K}{{{\tilde{x}}}_{1}}-{{k}_{1}}{{{\mathbf{\tilde{x}}}}_{2}} \end{align} \right.$ | (20) |
由于$\mathbf{W}_{o}^{*\text{T}}\phi \left( \mathbf{x},{{w}^{*}},{{c}^{*}} \right)-\mathbf{\hat{W}}_{o}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)\text{=}\mathbf{W}_{o}^{*\text{T}}\tilde{\phi }+\mathbf{\tilde{W}}_{o}^{\text{T}}\hat{\phi }$,式(20)可改写为:
| $\left\{ \begin{align} & {{{\mathbf{\dot{\tilde{x}}}}}_{1}}={{{\mathbf{\tilde{x}}}}_{2}}-{{\mathbf{k}}_{2}}{{{\mathbf{\tilde{x}}}}_{1}} \\ & {{{\mathbf{\dot{\tilde{x}}}}}_{2}}=\mathbf{W}_{o}^{*\text{T}}\tilde{\phi }+\mathbf{\tilde{W}}_{o}^{\text{T}}\hat{\phi }+{{\mathbf{\varepsilon }}_{o}}\left( \mathbf{x} \right)-\mathbf{K}{{{\tilde{x}}}_{1}}-{{\mathbf{k}}_{1}}{{{\mathbf{\tilde{x}}}}_{2}} \\ \end{align} \right.$ | (21) |
其中:$\tilde{\phi }\text{=}\phi -\hat{\phi },\phi \text{=}\phi \left( \mathbf{x},{{w}^{*}},{{c}^{*}} \right),\hat{\phi }\text{=}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)$。权值矩阵估计误差为${{\mathbf{\tilde{W}}}_{o}}=\mathbf{W}_{o}^{*}-{{\mathbf{\hat{W}}}_{o}}$。设计观测器神经网络权值矩阵的自适应律为:
| ${{\mathbf{\dot{\tilde{W}}}}_{o}}=-{{\mathbf{K}}_{{{\mathbf{W}}_{o}}}}\mathbf{\tilde{x}}_{1}^{\text{T}}\hat{\phi }+{{\gamma }_{o}}{{\mathbf{K}}_{{{\mathbf{W}}_{o}}}}\left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|{{\mathbf{\hat{W}}}_{o}}$ | (22) |
其中:KWo为正对角阵;γo为正常数。
2.2 控制器设计定义关节角度跟踪误差为e,角速度跟踪误差为,具体描述如下:
| $\left\{ \begin{align} & \mathbf{e}={{\mathbf{\theta }}_{d}}-\mathbf{\theta }={{\mathbf{\theta }}_{d}}-{{\mathbf{x}}_{1}} \\ & \mathbf{\dot{e}}={{{\mathbf{\dot{\theta }}}}_{d}}-\mathbf{\dot{\theta }}={{{\mathbf{\dot{\theta }}}}_{d}}-{{\mathbf{x}}_{2}} \\ \end{align} \right.$ | (23) |
定义跟踪误差为:
| $\mathbf{\hat{s}}=\mathbf{\dot{\hat{e}}}+\mathbf{\Lambda e}$ | (24) |
其中:Λ为正定阵。根据式(23)、(24)且${{\mathbf{\tilde{x}}}_{2}}={{\mathbf{x}}_{2}}-{{\mathbf{\hat{x}}}_{2}}$,角速度跟踪误差可表示为:
| $\mathbf{\dot{e}}=\mathbf{\hat{s}}-{{\mathbf{\tilde{x}}}_{2}}-\mathbf{\Lambda e}$ | (25) |
依据式(13),并结合式(24)、(25),慢变子系统动力学误差方程可表示为:
| ${{\mathbf{D}}_{r}}\left( {{\mathbf{x}}_{1}} \right)\mathbf{\dot{\hat{s}}}=-{{\mathbf{h}}_{r}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)\mathbf{\hat{s}}+{{\mathbf{h}}_{c}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)-\mathbf{u}$ | (26) |
| ${{\mathbf{h}}_{c}}={{\mathbf{D}}_{r}}\left( {{\mathbf{x}}_{1}} \right)\left( {{{\mathbf{\ddot{\theta }}}}_{d}}+{{{\mathbf{\dot{\tilde{x}}}}}_{2}} \right)+{{\mathbf{h}}_{r}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)\left( {{{\mathbf{\dot{\theta }}}}_{d}}+{{{\mathbf{\tilde{x}}}}_{2}} \right)+{{\mathbf{\tau }}_{d}}+\mathbf{\delta }$ | (27) |
对未知非线性系统基于模糊RBF神经网络的最优逼近可描述为:
| ${{\mathbf{h}}_{c}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)\text{=}{{\mathbf{f}}_{c}}\left( \mathbf{x},w,c,\mathbf{W}_{c}^{*} \right)=\mathbf{W}_{c}^{*\text{T}}\phi \left( \mathbf{x},{{w}^{*}},{{c}^{*}} \right)+{{\mathbf{\varepsilon }}_{c}}\left( \mathbf{x} \right)$ | (28) |
其中:逼近误差εc(x)满足‖εc(x)‖≤εcM,最优权值矩阵W*c满足‖W*c‖≤WcM。定义=$\mathbf{\hat{x}}=\left( {{{\mathbf{\hat{x}}}}_{1}},{{{\mathbf{\hat{x}}}}_{2}} \right)$,则利用神经网络的控制器估计输出为:
| ${{\mathbf{f}}_{c}}\left( \mathbf{\hat{x}},\hat{w},\hat{c},{{{\mathbf{\hat{W}}}}_{c}} \right)=\mathbf{\hat{W}}_{c}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)$ | (29) |
设计控制律u和鲁棒控制项为:
| $\mathbf{u}\text{=}\mathbf{\hat{W}}_{c}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)+{{\mathbf{K}}_{p}}\mathbf{e}+{{\mathbf{K}}_{d}}\mathbf{\dot{\hat{e}}}+\mathbf{\hat{v}}$ | (30) |
| $\mathbf{\hat{v}}={{\mathbf{\hat{s}}}}/{{{k}_{v}}}\;$ | (31) |
其中:Kp、Kd为正定阵,kv>0。将式(28)、(30)代入式(26)中,并由$\mathbf{W}_{c}^{*\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)-\mathbf{\hat{W}}_{c}^{\text{T}}\phi \left( \mathbf{\hat{x}},\hat{w},\hat{c} \right)\text{=}\mathbf{W}_{c}^{*\text{T}}\tilde{\phi }+\mathbf{\tilde{W}}_{c}^{\text{T}}\hat{\phi }$,可得:
| ${{\mathbf{D}}_{r}}\left( {{\mathbf{x}}_{1}} \right)\mathbf{\dot{\hat{s}}}=-{{\mathbf{h}}_{r}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)\mathbf{\dot{\hat{s}}}+\mathbf{W}_{c}^{*\text{T}}\tilde{\phi }+\mathbf{\tilde{W}}_{c}^{\text{T}}\hat{\phi }+{{\mathbf{\varepsilon }}_{c}}\left( \mathbf{x} \right)-{{\mathbf{K}}_{p}}\mathbf{e}-{{\mathbf{K}}_{d}}\mathbf{\dot{\hat{e}}}-\mathbf{\hat{v}}$ | (32) |
为保证系统的稳定性和关节轨迹跟踪的精度,并在线调节模糊基函数的中心和半径,本文利用一阶泰勒展开式对非线性部分进行线性化处理[20],可得:
| $\tilde{\phi }\text{=}{{\mathbf{H}}^{\text{T}}}\mathbf{\tilde{w}}+{{\mathbf{Q}}^{\text{T}}}\mathbf{\tilde{c}}+{{\mathbf{G}}^{\text{T}}}{{\mathbf{\tilde{x}}}_{1}}+{{\mathbf{R}}^{\text{T}}}{{\mathbf{\tilde{x}}}_{2}}+\mathbf{h}\text{=}\frac{\partial \phi }{\partial \mathbf{w}}\mathbf{\tilde{w}}+\frac{\partial \phi }{\partial \mathbf{c}}\mathbf{\tilde{c}}+\frac{\partial \phi }{\partial {{\mathbf{x}}_{1}}}{{\mathbf{\tilde{x}}}_{1}}+\frac{\partial \phi }{\partial {{\mathbf{x}}_{2}}}{{\mathbf{\tilde{x}}}_{2}}+\mathbf{h}$ | (33) |
其中:$\mathbf{h}=\mathbf{h}\left( \mathbf{\tilde{w}},\mathbf{\tilde{c}},{{{\mathbf{\tilde{x}}}}_{1}},{{{\mathbf{\tilde{x}}}}_{2}} \right)$为泰勒展开式高阶余项。
假设1 矩阵H、Q、G、R有界,即存在正常数阵HM、QM、GM、RM满足‖H‖≤HM,‖Q‖≤QM,‖G‖≤GM,‖R‖≤RM。
考虑到$\tilde{\phi }-{{\mathbf{G}}^{\text{T}}}{{\mathbf{\tilde{x}}}_{1}}-{{\mathbf{R}}^{\text{T}}}{{\mathbf{\tilde{x}}}_{2}}-\mathbf{h}\text{=}{{\mathbf{H}}^{\text{T}}}\mathbf{\tilde{w}}+{{\mathbf{Q}}^{\text{T}}}\mathbf{\tilde{c}}$,则将式(32)改写为:
| $\begin{align} & {{\mathbf{D}}_{r}}\left( {{\mathbf{x}}_{1}} \right)\mathbf{\dot{\hat{s}}}=-{{\mathbf{h}}_{r}}\left( {{\mathbf{x}}_{1}},{{\mathbf{x}}_{2}} \right)\mathbf{\dot{\hat{s}}}+\mathbf{\tilde{W}}_{c}^{\text{T}}\left( \tilde{\phi }-{{\mathbf{H}}^{\text{T}}}\mathbf{\tilde{w}}-{{\mathbf{Q}}^{\text{T}}}\mathbf{\tilde{c}} \right)+ \\ & \mathbf{\hat{W}}_{c}^{\text{T}}\left( {{\mathbf{H}}^{\text{T}}}\mathbf{\tilde{w}}+{{\mathbf{Q}}^{\text{T}}}\mathbf{\tilde{c}} \right)+{{\mathbf{d}}_{c}}-{{\mathbf{K}}_{p}}\mathbf{e}-{{\mathbf{K}}_{d}}\mathbf{\dot{\hat{e}}}-\mathbf{\hat{v}} \\ \end{align}$ | (34) |
| ${{\mathbf{d}}_{c}}=\mathbf{\tilde{W}}_{c}^{\text{T}}\left( {{\mathbf{H}}^{\text{T}}}{{\mathbf{w}}^{*}}+{{\mathbf{Q}}^{\text{T}}}{{\mathbf{c}}^{*}} \right)+\mathbf{W}_{c}^{*\text{T}}\left( \tilde{\phi }-{{\mathbf{H}}^{\text{T}}}\mathbf{\tilde{w}}-{{\mathbf{Q}}^{\text{T}}}\mathbf{\tilde{c}} \right)+{{\mathbf{\varepsilon }}_{c}}\left( x \right)$ | (35) |
其中:dc有界且满足:
| ${{\mathbf{d}}_{c}}\le \left\| \mathbf{\tilde{W}}_{c}^{\text{T}} \right\|\left\| {{\mathbf{H}}^{\text{T}}}{{\mathbf{w}}^{*}}+{{\mathbf{Q}}^{\text{T}}}{{\mathbf{c}}^{*}} \right\|+\left\| \mathbf{W}_{c}^{*\text{T}}{{\mathbf{H}}^{\text{T}}} \right\|\left\| {\mathbf{\tilde{w}}} \right\|+\left\| \mathbf{W}_{c}^{*\text{T}}{{\mathbf{Q}}^{\text{T}}} \right\|\left\| {\mathbf{\tilde{c}}} \right\|+\left\| \mathbf{W}_{c}^{*\text{T}}\tilde{\phi }+{{\mathbf{\varepsilon }}_{c}}\left( \mathbf{x} \right) \right\|$ | (36) |
定义实际值矩阵${{\mathbf{\Theta }}^{*}}=\text{diag}\left( \mathbf{W}_{c}^{*},\mathbf{w}_{c}^{*},\mathbf{c}_{c}^{*} \right)$,估计值矩阵$\mathbf{\hat{\Theta }}=\text{diag}\left( {{{\mathbf{\hat{W}}}}_{c}},{{{\mathbf{\hat{w}}}}_{c}},{{{\mathbf{\hat{c}}}}_{c}} \right)$。由假设1可知,存在正常数阵,满足$\left\| {{\mathbf{\Theta }}^{*}} \right\|\le {{\mathbf{\Theta }}_{M}}$。
设计控制器神经网络权值矩阵的自适应律为:
| ${{{\mathbf{\dot{\tilde{W}}}}}_{c}}=-{{\mathbf{K}}_{{{W}_{c}}}}\mathbf{Z}{{{\mathbf{\hat{s}}}}^{\text{T}}}+{{\gamma }_{c}}{{\mathbf{K}}_{{{W}_{c}}}}\left\| {\mathbf{\hat{s}}} \right\|{{{\mathbf{\hat{W}}}}_{c}}$ | (37) |
| $\mathbf{Z}=\hat{\phi }-{{\mathbf{H}}^{\text{T}}}\mathbf{\hat{w}}-{{\mathbf{Q}}^{\text{T}}}\mathbf{\hat{c}}$ | (38) |
| $\mathbf{\dot{\tilde{w}}}=-{{\mathbf{K}}_{w}}\mathbf{H}{{{\mathbf{\hat{W}}}}_{c}}\mathbf{\hat{s}}+{{\gamma }_{c}}{{\mathbf{K}}_{w}}\left\| {\mathbf{\hat{s}}} \right\|\mathbf{\hat{w}}$ | (39) |
| $\mathbf{\dot{\tilde{c}}}=-{{\mathbf{K}}_{c}}\mathbf{Q}{{{\mathbf{\hat{W}}}}_{c}}\mathbf{\hat{s}}+{{\gamma }_{c}}{{\mathbf{K}}_{c}}\left\| {\mathbf{\hat{s}}} \right\|\mathbf{\hat{c}}$ | (40) |
其中:KWc,Kw,Kc为对角阵,γc为正常数。
2.3 稳定性分析定理1 对于慢变子系统(12),当假设1成立时,采用控制律(30)和自适应律(22)、(37)~(40)。存在增益矩阵K>0,Kp>0,Kd>0,常数k1>0,k2>0,kv>0,且满足${{\mathbf{K}}_{p}}\mathbf{\Lambda }-\frac{1}{2}{{\mathbf{K}}_{p}}-\frac{1}{2}{{\mathbf{K}}_{d}}\mathbf{\Lambda }>0,{{\mathbf{K}}_{d}}\mathbf{\Lambda }-\frac{1}{2}{{\mathbf{K}}_{d}}\mathbf{\Lambda }+\frac{1}{{{k}_{v}}}\mathbf{I}>0$时,慢变子系统一致最终有界。
证明 定义如下的李雅普诺夫函数:
| $\mathbf{V}={{\mathbf{V}}_{o}}+{{\mathbf{V}}_{c}}$ | (41) |
| ${{\mathbf{V}}_{o}}=\frac{1}{2}\mathbf{\tilde{x}}_{1}^{\text{T}}\mathbf{K}{{{\mathbf{\tilde{x}}}}_{1}}+\frac{1}{2}\mathbf{\tilde{x}}_{2}^{\text{T}}{{{\mathbf{\tilde{x}}}}_{2}}+\frac{1}{2}\text{tr}\left( \mathbf{\tilde{W}}_{o}^{\text{T}}\mathbf{K}_{{{W}_{o}}}^{-1}{{{\mathbf{\tilde{W}}}}_{o}} \right)$ | (42) |
| ${{\mathbf{V}}_{c}}=\frac{1}{2}{{\mathbf{e}}^{\text{T}}}{{\mathbf{K}}_{p}}\mathbf{e}+\frac{1}{2}{{{\mathbf{\hat{s}}}}^{\text{T}}}{{\mathbf{D}}_{r}}\mathbf{\hat{s}}+\frac{1}{2}\text{tr}\left( \mathbf{\tilde{W}}_{c}^{\text{T}}\mathbf{K}_{{{W}_{c}}}^{-1}{{{\mathbf{\tilde{W}}}}_{c}} \right)+\frac{1}{2}\text{tr}\left( {{{\mathbf{\tilde{w}}}}^{\text{T}}}\mathbf{K}_{w}^{-1}\mathbf{\tilde{w}} \right)+\frac{1}{2}\text{tr}\left( {{{\mathbf{\tilde{c}}}}^{\text{T}}}\mathbf{K}_{c}^{-1}\mathbf{\tilde{c}} \right)$ | (43) |
将式(42)两端同时关于时间求导,并将式(21)、(22)代入,定义${{\mathbf{k}}_{2}}\mathbf{\tilde{W}}_{o}^{\text{T}}\hat{\phi }={{\mathbf{d}}_{1}},\mathbf{W}_{o}^{*\text{T}}\tilde{\phi }+\mathbf{\tilde{W}}_{o}^{\text{T}}\hat{\phi }+{{\mathbf{\varepsilon }}_{o}}\left( \mathbf{x} \right)={{\mathbf{d}}_{2}}$,可得:
| ${{\mathbf{\dot{V}}}_{o}}=-{{\mathbf{k}}_{2}}\mathbf{\tilde{x}}_{1}^{\text{T}}\mathbf{K}{{\mathbf{\tilde{x}}}_{1}}+\mathbf{\tilde{x}}_{2}^{\text{T}}{{\mathbf{d}}_{2}}-\mathbf{\tilde{x}}_{2}^{\text{T}}{{\mathbf{k}}_{1}}{{\mathbf{\tilde{x}}}_{2}}+\mathbf{\tilde{x}}_{1}^{\text{T}}{{\mathbf{d}}_{1}}+\text{tr}\left( \mathbf{\tilde{W}}_{o}^{\text{T}}{{\gamma }_{o}}\left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|{{{\mathbf{\hat{W}}}}_{o}} \right)$ | (44) |
将式(43)两端同时关于时间求导,将式(34)和控制器自适应律(37)~(40)代入,利用性质1可得:
| $\begin{align} & {{{\mathbf{\dot{V}}}}_{c}}=-{{\mathbf{e}}^{\text{T}}}{{\mathbf{K}}_{p}}{{{\mathbf{\tilde{x}}}}_{2}}-{{\mathbf{e}}^{\text{T}}}{{\mathbf{k}}_{p}}\mathbf{\Lambda e}-{{{\mathbf{\hat{s}}}}^{\text{T}}}{{\mathbf{K}}_{d}}\mathbf{\hat{s}}+{{{\mathbf{\hat{s}}}}^{\text{T}}}{{\mathbf{K}}_{d}}\mathbf{\Lambda e}-{{{\mathbf{\hat{s}}}}^{\text{T}}}\mathbf{\hat{v}}+{{{\mathbf{\hat{s}}}}^{\text{T}}}{{\mathbf{d}}_{c}}+ \\ & \text{tr}\left( \mathbf{\tilde{W}}_{c}^{\text{T}}{{\gamma }_{c}}\left\| {\mathbf{\hat{s}}} \right\|{{{\mathbf{\hat{W}}}}_{c}} \right)+\text{tr}\left( {{{\mathbf{\tilde{w}}}}^{\text{T}}}{{\gamma }_{c}}\left\| {\mathbf{\hat{s}}} \right\|\mathbf{\hat{w}} \right)+\text{tr}\left( {{{\mathbf{\tilde{c}}}}^{\text{T}}}{{\gamma }_{c}}\left\| {\mathbf{\hat{s}}} \right\|{{{\mathbf{\hat{c}}}}_{c}} \right) \\ \end{align}$ | (45) |
考虑到2ab≤a2+b2,并结合式(44)、(45),将$\text{tr}\left( {{\mathbf{A}}^{\text{T}}}\mathbf{B} \right)\le \left\| \mathbf{A} \right\|\left\| \mathbf{B} \right\|$和=$\mathbf{\tilde{W}}={{\mathbf{W}}^{*}}-\mathbf{\hat{W}}$代入化简可得:
| $\begin{align} & \mathbf{\dot{V}}\le \mathbf{\tilde{x}}_{1}^{\text{T}}{{\mathbf{d}}_{1}}-{{\mathbf{k}}_{2}}\mathbf{\tilde{x}}_{1}^{\text{T}}\mathbf{K}{{{\mathbf{\tilde{x}}}}_{1}}-\frac{1}{2}{{{\mathbf{\tilde{x}}}}^{\text{T}}}\left( 2{{k}_{1}}\mathbf{I}+{{\mathbf{K}}_{p}} \right){{{\mathbf{\tilde{x}}}}_{2}}+ \\ & \mathbf{\tilde{x}}_{2}^{\text{T}}{{\mathbf{d}}_{2}}-\frac{1}{2}{{{\mathbf{\hat{s}}}}^{\text{T}}}\left( 2{{\mathbf{K}}_{d}}-{{\mathbf{K}}_{d}}\mathbf{\Lambda }+\frac{2}{{{k}_{v}}}\mathbf{I} \right)\mathbf{\hat{s}}+{{{\mathbf{\hat{s}}}}^{\text{T}}}{{\mathbf{d}}_{c}}- \\ & {{\mathbf{e}}^{\text{T}}}\left( {{\mathbf{K}}_{p}}\mathbf{\Lambda }- \right.\left. \frac{1}{2}{{\mathbf{K}}_{p}}-\frac{1}{2}{{\mathbf{K}}_{d}}\mathbf{\Lambda } \right)\mathbf{e}+{{\gamma }_{o}}\left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|\cdot \left( \left\| \mathbf{\tilde{W}}_{o}^{\text{T}} \right\|\left( \left\| {{\mathbf{W}}_{o}}^{*} \right\|-\left\| {{{\mathbf{\tilde{W}}}}_{o}} \right\| \right) \right)+ \\ & {{\gamma }_{c}}\left\| {\mathbf{\hat{s}}} \right\|\left( \left\| {{{\mathbf{\tilde{\Theta }}}}^{\text{T}}} \right\|\left( \left\| {{\mathbf{\Theta }}^{*}} \right\|-\left\| {\mathbf{\tilde{\Theta }}} \right\| \right) \right) \\ \end{align}$ | (46) |
考虑到$\left\| {\hat{\phi }} \right\|\le \sqrt{n}$,n为神经网络节点数,且dc、d1、d2均有界,分别定义其上界为:
| ${{\mathbf{d}}_{cM}}=2\left( {{\mathbf{H}}_{M}}{{\mathbf{w}}_{M}}+{{\mathbf{Q}}_{M}}{{\mathbf{c}}_{M}} \right)+\sqrt{n}{{\mathbf{W}}_{cM}}+{{\mathbf{\varepsilon }}_{cM}}$ | (47) |
| ${{\mathbf{d}}_{1M}}=2{{k}_{2}}\sqrt{n}{{\mathbf{W}}_{oM}}$ | (48) |
| ${{\mathbf{d}}_{2M}}=3\sqrt{n}{{\mathbf{W}}_{oM}}+{{\mathbf{\varepsilon }}_{oM}}$ | (49) |
则式(46)可化简为:
| $\begin{align} & \mathbf{\dot{V}}\le -\left\| \mathbf{s} \right\|\left\{ {{\mathbf{K}}_{s}}\left\| \mathbf{s} \right\|+{{\gamma }_{c}}{{\left( \left\| {\mathbf{\tilde{\Theta }}} \right\|-{{\mathbf{\lambda }}_{s}} \right)}^{2}}-{{\mathbf{\rho }}_{s}} \right\}- \\ & \left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|\left\{ {{\mathbf{K}}_{{{\mathbf{x}}_{1}}}} \right.\text{ }\left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|+\left. {{\gamma }_{o}}{{\left( \left\| {{{\mathbf{\tilde{W}}}}_{o}} \right\|-{{\mathbf{\lambda }}_{{{\mathbf{x}}_{1}}}} \right)}^{2}}-{{\mathbf{\rho }}_{1}} \right\}-\left\| {{{\mathbf{\tilde{x}}}}_{2}} \right\|\left\{ \left\{ {{\mathbf{K}}_{{{\mathbf{x}}_{2}}}} \right.\left\| {{{\mathbf{\tilde{x}}}}_{2}} \right\|-{{\mathbf{\rho }}_{2}} \right\} \\ \end{align}$ | (50) |
其中: $\begin{align} & {{\mathbf{\rho }}_{s}}={{\gamma }_{c}}\mathbf{\lambda }_{s}^{2}+{{\mathbf{d}}_{cM}},{{\mathbf{\rho }}_{2}}={{\mathbf{d}}_{2M}},{{\mathbf{\lambda }}_{s}}={{{\mathbf{\Theta }}_{M}}}/{2}\;,{{\mathbf{\lambda }}_{{{\mathbf{x}}_{1}}}}={{{\mathbf{W}}_{oM}}}/{2}\;, \\ & {{\mathbf{K}}_{s}}={{\mathbf{K}}_{d}}\mathbf{\Lambda }-{{{\mathbf{K}}_{d}}\mathbf{\Lambda }}/{2}\;-{\mathbf{I}}/{{{k}_{v}}}\;,{{\mathbf{K}}_{{{\mathbf{x}}_{1}}}}={{k}_{2}}\mathbf{K}{{\mathbf{K}}_{{{\mathbf{x}}_{2}}}}=2{{k}_{1}}\mathbf{I}+{{\mathbf{K}}_{p}} \\ \end{align}$。
在${{\mathbf{K}}_{s}}>0,{{\mathbf{K}}_{{{\mathbf{x}}_{1}}}}>0,{{\mathbf{K}}_{{{\mathbf{x}}_{2}}}}>0$条件下,若式(50)满足:
| $\left\| \mathbf{s} \right\|>\frac{{{\mathbf{\rho }}_{s}}}{{{\mathbf{K}}_{s}}}\text{ or }\left\| {\mathbf{\tilde{\Theta }}} \right\|>\sqrt{\frac{{{\mathbf{\rho }}_{s}}}{{{\gamma }_{c}}}}+{{\mathbf{\lambda }}_{s}}$ | (51) |
| $\left\| {{{\mathbf{\tilde{x}}}}_{1}} \right\|>\frac{{{\mathbf{\rho }}_{1}}}{{{\mathbf{K}}_{{{\mathbf{x}}_{1}}}}}\text{ or }\left\| {{{\mathbf{\tilde{W}}}}_{o}} \right\|>\sqrt{\frac{{{\mathbf{\rho }}_{1}}}{{{\gamma }_{o}}}}+{{\mathbf{\lambda }}_{{{\mathbf{x}}_{1}}}}$ | (52) |
| $\left\| {{{\mathbf{\tilde{x}}}}_{2}} \right\|>\frac{{{\mathbf{\rho }}_{1}}}{{{\mathbf{K}}_{{{\mathbf{x}}_{2}}}}}$ | (53) |
则$\mathbf{\dot{V}}\le 0$。证毕。
由此可知,可以通过对参数的调节来满足观测器和控制器的稳定,并使关节轨迹跟踪误差和估计误差在任意小的范围内,保证一致最终有界。则力矩受限的跟踪控制律为:
| ${{\mathbf{\tau }}_{s}}={{\mathbf{\tau }}_{\max }}\tanh ({\mathbf{u}}/{{{\mathbf{\tau }}_{\max }}}\;)$ | (54) |
其中:τmax为所设定的机械臂关节最大输出力矩。
3 基于ESO的LQR控制器设计为更加精确地进行快变子系统的控制器设计,需考虑柔性振动系统中的不确定部分,式(11)改写为:
| $\mathbf{\dot{\zeta }}\text{=}{{\mathbf{A}}_{f}}\mathbf{\zeta }+{{\mathbf{B}}_{f}}{{\mathbf{\tau }}_{f}}+{{\mathbf{B}}_{d}}\mathbf{{\delta }'}$ | (55) |
其中:
| $\begin{align} & \mathbf{\zeta }\text{=}{{\left[ {{\zeta }_{1}}\text{ }{{\zeta }_{2}} \right]}^{\text{T}}} \\ & {{\mathbf{A}}_{f}}=\left[ \begin{matrix} 0 & \mathbf{I} \\ -{{\mathbf{N}}_{22}}\mathbf{\tilde{K}} & 0 \\ \end{matrix} \right] \\ & {{\mathbf{B}}_{f}}=\left[ \begin{matrix} 0 \\ {{\mathbf{N}}_{21}} \\ \end{matrix} \right] \\ \end{align}$ |
δ′表示快变子系统的不确定部分,包括建模误差、外界扰动等。
假设2 未知不确定部分δ′可微,即扰动变化率′有界,$\forall t\in {{\text{R}}_{+}}$满足$\left| {\mathbf{{\dot{\delta }}'}} \right|\le \gamma $,γ为大于零的实常数[21]。
定义快变子系统的输出向量:
| $y=\mathbf{C\zeta }=\left[ I\text{ 0} \right]{{\left[ {{\zeta }_{1}}\text{ }{{\zeta }_{2}} \right]}^{\text{T}}}$ | (56) |
并假定输出变量y可通过测量方式获得。
由于(Af,Bf,C)可控可观,则利用状态观测器估计值构成状态反馈时,其系统的状态反馈和观测器可分别设计。
对系统进行状态反馈设计时,针对标称系统,采用LQR进行柔性振动抑制,使系统状态ζ调节到零。以抑制振动和减少能量消耗为优化目标,构造性能指标函数如下:
| $\mathbf{J}=\frac{1}{2}\int_{0}^{\infty }{\left( {{\mathbf{\zeta }}^{\text{T}}}\mathbf{Q\zeta }+\mathbf{\tau }_{f1}^{\text{T}}\mathbf{R}{{\mathbf{\tau }}_{f1}} \right)}\text{ dt}$ | (57) |
其中:Q和R分别表示状态向量ζ和控制向量τf1对性能指标影响的相对重要性所占权重。则快变子系统的最优控制为:
| ${{\mathbf{\tau }}_{f1}}=-\mathbf{K\zeta }=-{{\mathbf{R}}^{-1}}\mathbf{B}_{f}^{\text{T}}\mathbf{P\zeta }$ | (58) |
其中:P为$\mathbf{P}{{\mathbf{A}}_{f}}+\mathbf{A}_{f}^{\text{T}}\mathbf{P}-\mathbf{P}{{\mathbf{B}}_{f}}{{\mathbf{R}}^{-1}}\mathbf{B}_{f}^{\text{T}}\mathbf{P}+\mathbf{Q}=\mathbf{0}$方程的解。
针对控制率中的不确定补偿项τf2取:
| ${{\mathbf{\tau }}_{f2}}=-{{\mathbf{{\delta }'}}}/{b}\;$ | (59) |
将τf=τf1+τf2代入式(55)可得:
| $\left\{ \begin{align} & \mathbf{\dot{\zeta }}\text{=}{{\mathbf{A}}_{f}}\mathbf{\zeta }+{{\mathbf{B}}_{f}}{{\mathbf{\tau }}_{f}} \\ & y=\mathbf{C\zeta } \\ \end{align} \right.$ | (60) |
故τf能够保证快变子系统对不确定部分具有强鲁棒性。由于模态坐标导数的测量较为困难,易引入噪声误差,且不确定部分δ′无法直接测量,为此引入扩张状态观测器(ESO)对不确定系统进行状态估计并用于状态反馈。将δ′视为一个扩张状态,在系统(55)的基础上得到状态扩张系统为:
| $\left\{ \begin{align} & {{{\mathbf{\dot{\zeta }}}}_{E}}\text{=}{{\mathbf{A}}_{E}}{{\mathbf{\zeta }}_{E}}+{{\mathbf{B}}_{E}}{{\mathbf{\tau }}_{f}}+{{\mathbf{B}}_{D}}\mathbf{{\dot{\delta }}'} \\ & y={{\mathbf{C}}_{E}}{{\mathbf{\zeta }}_{E}} \\ \end{align} \right.$ | (61) |
其中: ζE=[ζ δ′]T为扩张的状态向量,′为不确定部分变化率,
针对系统(61)设计扩张状态观测器(ESO):
| $\left\{ \begin{align} & {{{\dot{\hat{\zeta }}}}_{1}}={{{\hat{\zeta }}}_{2}}+{{\beta }_{1}}{{g}_{1}}\left( {{e}_{o1}} \right) \\ & {{{\dot{\hat{\zeta }}}}_{2}}=-{{N}_{22}}\tilde{K}{{{\hat{\zeta }}}_{1}}+{{N}_{21}}{{\tau }_{f}}+b\hat{\delta }+{{\beta }_{2}}{{g}_{2}}\left( {{e}_{o1}} \right) \\ & \dot{\hat{\delta }}={{\beta }_{3}}{{g}_{3}}\left( {{e}_{o1}} \right) \\ \end{align} \right.$ | (62) |
其中:${{\hat{\zeta }}_{i}},i=1,2$为状态${{\hat{\zeta }}_{i}}$的估计值;${\dot{\hat{\delta }}}'$为${\hat{\delta }}'$的估计值;${{e}_{o1}}=y-{{\hat{\zeta }}_{1}}$; βi为观测器增益;gi为非线性函数,对任意eo1≠0,gi(0)=0,满足eo1gi(eo1)>0。gi的选择极其关键,目前大多数采用如下带有线性区的非线性函数:
| ${g_i}\left( {{e_{o1}}} \right) = \left\{ \matrix{ {\left| {{e_{o1}}} \right|^{{\mu _i}}}{\mathop{\rm sgn}} \left( {{e_{o1}}} \right)\left| {{e_{o1}}} \right| > \alpha \hfill \cr {e_{o1}}/{\alpha ^{1 - {\mu _i}}}\left| {{e_{o1}}} \right| \le \alpha \hfill \cr} \right.$ | (63) |
其中:0<μi<1,α>0为gi切换的阈值。可见,只要βi和gi选择恰当,状态估计值${{\hat{\zeta }}_{i}}$和${\hat{\delta }}'$就能精确逼近实际值。此外,ESO观测所用状态量均可测且原理简单,无需复杂的在线辨识,易于实现。结合式(57)~(58),取gi(eo1)=eo1,可得:
| $\left\{ \begin{align} & {{{\mathbf{\dot{\hat{\zeta }}}}}_{E}}\text{=}{{\mathbf{A}}_{E}}{{{\mathbf{\hat{\zeta }}}}_{E}}+{{\mathbf{B}}_{E}}{{\mathbf{\tau }}_{f}}+{{\mathbf{H}}_{k}}{{e}_{o1}} \\ & \mathbf{y}={{\mathbf{C}}_{E}}{{{\mathbf{\hat{\zeta }}}}_{E}} \\ \end{align} \right.$ | (64) |
其中:Hk=[β1 β2 β3]为待确定的观测增益向量。通过式(59)可完成对系统状态的估计,此时快变子系统控制律为:
| ${{\mathbf{\tau }}_{f}}=-\mathbf{\bar{K}}{{\mathbf{\hat{\zeta }}}_{E}}$ | (65) |
其中:K=[K 1/b]。
利用式(7),将慢变子系统的RBF神经网络自适应部分τs与快变子系统LQR部分τf相结合,得到满足控制目标的力矩τ。系统的整体框图如图 3所示。
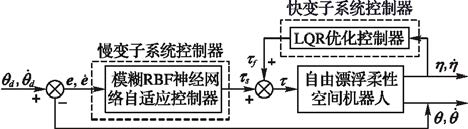
|
图 3 控制系统整体框图 |
以图 1所示平面自由漂浮柔性空间机器人为例,验证本文方法的有效性。系统惯性参数见表 1所示。
| 表 1 空间机器人模型惯性参数 |
B2杆单位长度的密度为ρ=1 kg/m,均匀弯曲刚度为EI=200 Pa。仿真时假设柔性空间机器人关节铰的期望运动轨迹为θd(t)=[sin t,sin t]T(rad),初始角度为θ0=[0,0]T(rad),柔性杆的初始、期望模态坐标均为η0=ηd=[0,0]T(m)。
选取慢变子系统控制参数如下:隐含层神经元个数n=25,误差函数参数Λ=diag(8,8);观测器增益为K=diag(80,80),k1=60,k2=16,观测器自适应律参数为KWo=diag(20,20),γ0=0.005;kv=0.003,Kd=diag(80,80)为控制器增益;γc=0.01,Kp=diag(50,50),KWc=diag(80,80),KW=diag(60,60),Kc=diag(30,30)为控制器自适应律参数; τd=[0.2 sin t,0.15 cos t]T(rad)为不确定部分。模糊RBF神经网络的初始权值,基函数的中心和宽度均为(0,0.01)内的任意一个随机数。
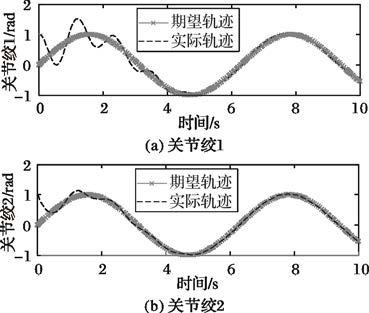
选取快变子系统权值阵Q(ζ)=104×diag(8,8,8,8),R(ζ)=10-1×diag(2,2),观测器参数β1= β2=100,β3=200,μ1= μ2= μ3=0.5,α=0.01,不确定部分δ=[0.001 sin t,0.001 cos t]T(rad)。 仿真时间为10.0 s。图 4~9为关节轨迹跟踪仿真结果,图 10~11为柔性振动抑制仿真结果。
|
图 4 文献[13]方法轨迹跟踪示意图 |
|
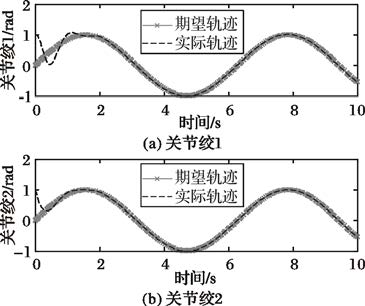
图 5 本文方法轨迹跟踪示意图 |
|
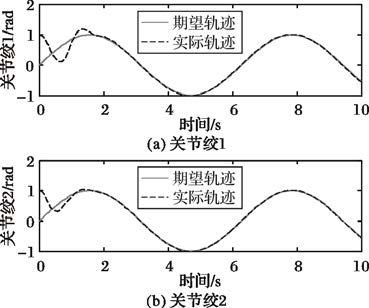
图 6 力矩受限轨迹跟踪示意图 |
|
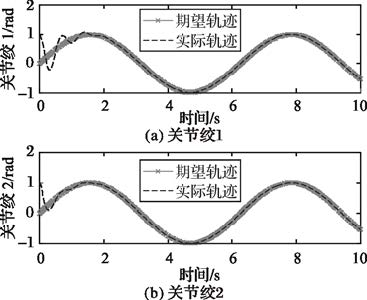
图 7 噪声扰动轨迹跟踪示意图 |
|
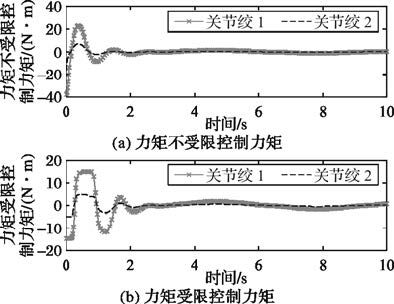
图 8 关节输出力矩对比 |
|
图 9 关节轨迹跟踪误差对比 |
文献[13]设计了一种基于速度观测器的神经网络自适应鲁棒控制器,针对不确定机械臂进行轨迹跟踪控制,能够保证权值估计误差有界,轨迹跟踪误差渐进收敛。但所设计的观测器需要精确的惯性参数,仅对神经网络权值矩阵进行自适应调节,在参数未知情况下,控制器效果不佳。本文所设计的模糊RBF神经网络自适应控制方法不仅可以调节权值矩阵,还可对隐含层参数进行调整,在慢速运动条件下满足实时控制,有效消除了离线学习阶段,控制精度更优。图 4~5分别表示参数未知、力矩不受限情况下文献[13]和本文所设计控制器的关节轨迹跟踪示意图。不难发现,本文所设计控制方法较文献[13]能更加精确快速稳定地完成期望轨迹的渐进跟踪。
图 6为参数未知、力矩受限情况下本文所设计控制器的关节轨迹跟踪示意图,有效克服了力矩受限的影响,实现了对期望轨迹稳定的跟踪控制。
图 7为受到[-0.1,0.1]均匀分布的白噪声扰动时的关节轨迹跟踪示意图,虽然在跟踪前期存在一定的抖动,但仍能够较快跟踪期望轨迹,说明本文所设计控制器具有良好的抗干扰性和鲁棒性。
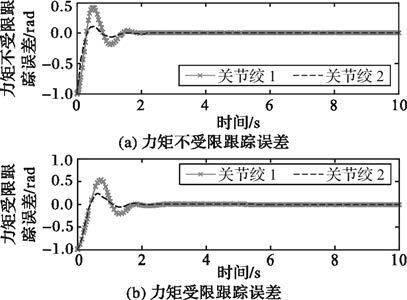
图 8为力矩约束前后,关节绞的控制力矩对比图。力矩约束前关节绞输出的控制力矩范围分别在-40~25 N·m和-20~10 N·m。假设关节绞可输出的控制力矩在±20 N·m和±10 N·m范围内,结合图 6可知,控制器在力矩受限下仍能稳定的跟踪期望轨迹,且将力矩有效限制在输出范围内。
图 9为力矩受限前后,关节轨迹跟踪的误差对比图。结合图 5~6,通过对比不难发现,力矩受限情况下,关节稳定跟踪期望轨迹所用时间较力矩不受限情况下稍长。由于对控制力矩进行约束,使得控制力矩实际输出未能达到期望值,从而延长了力矩作用时间,达到稳定跟踪状态所需时间更长。
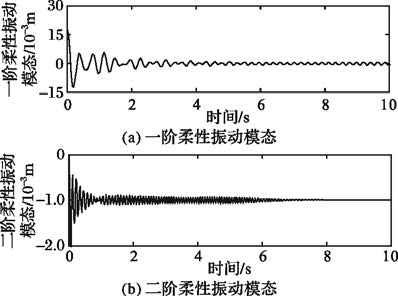
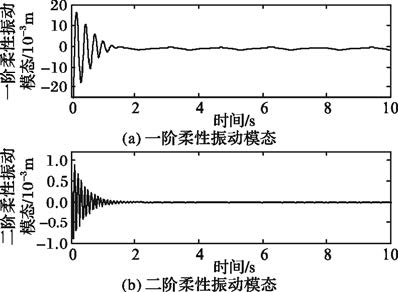
图 10~11分别为未经过主动抑制和主动抑制后的柔性振动一、二阶模态。不难发现,经主动抑制后的柔性振动模态幅值减小,收敛迅速,柔性振动幅值限制在±1×10-3m内。说明基于ESO和LQR的振动抑制优化控制器能够对柔性振动进行有效抑制。
|
图 10 未主动抑制柔性模态 |
|
图 11 主动抑制柔性模态 |
对于力矩受限与存在参数不确定性的自由漂浮柔性空间机器人系统,本文利用奇异摄动法提出一种基于速度观测器的模糊RBF神经网络自适应控制器和基于ESO和LQR的振动抑制优化控制器相结合的组合控制器设计方法,实现了关节轨迹的稳定跟踪和对柔性振动的有效抑制。理论推导和仿真分析表明:
1) 利用模糊RBF神经网络,观测器能够较好地估计关节角速度信息,同时对观测器和控制器的未知非线性进行动态补偿;
2) 所提控制方法在未知系统动力学模型,甚至未知惯性矩阵情况下,仍能确保精确的轨迹跟踪,同时可实现对神经网络权值矩阵和参数的实时在线调节,免除离线学习阶段,满足实时性要求;
3) 引入ESO对不易测量的柔性振动模态坐标导数和未知扰动进行估计,避免测量噪声的干扰以及不确定扰动,更贴合工程实际,有效抑制了柔性振动。
| [1] |
梁斌, 杜晓东, 李成, 等. 空间机器人非合作航天器在轨服务研究进展[J].
机器人, 2012, 34 (2) : 242-256.
( LIANG B, DU X D, LI C, et al. Advances in space robot on-orbit servicing for non-cooperative spacecraft[J].
Robot, 2012, 34 (2) : 242-256.
doi: 10.3724/SP.J.1218.2012.00242 ) ( 0) 0)
|
| [2] |
刘正雄, 黄攀峰. 基于递推差分进化算法的空间机器人参数辨识[J].
宇航学报, 2014, 35 (10) : 1127-1134.
( LIU Z X, HUANG P F. Parameter identification of space robot based on recursive different evolution algorithm[J].
Journal of Astronautics, 2014, 35 (10) : 1127-1134.
) ( 0) 0)
|
| [3] |
梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J].
宇航学报, 2010, 31 (1) : 1-13.
( LIANG B, XU W F, LI C, et al. The status and prospect of orbital servicing in the geostationary orbit[J].
Journal of Astronautics, 2010, 31 (1) : 1-13.
) ( 0) 0)
|
| [4] |
翟光, 张景瑞, 周志成. 静止轨道卫星在轨延寿技术研究进展[J].
宇航学报, 2012, 33 (7) : 122-134.
( ZHAI G, ZHANG J R, ZHOU Z C. A review of on-orbit life-time extension technologies for GEO satellites[J].
Journal of Astronautics, 2012, 33 (7) : 122-134.
) ( 0) 0)
|
| [5] |
WANG M, LI Y, REN X. Adaptive sliding mode control for hydraulic flexible manipulator based on two-parameter singular perturbation method[C]//Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics. Piscataway, NJ: IEEE, 2013: 57-60.
( 0) 0)
|
| [6] |
ZENG P L, WANG S X, QIU J J, et al. Flexible manipulator control based on singular perturbation theory study[J].
Applied Mechanics and Materials, 2013, 346 : 69-73.
doi: 10.4028/www.scientific.net/AMM.346 ( 0) 0)
|
| [7] |
洪在地, 贠超, 陈力. 漂浮基空间机器人及其柔性影响下逆模神经网络控制[J].
宇航学报, 2007, 28 (6) : 1510-1514.
( HONG Z D, YUN C, CHEN L. Inverse-model neuro-control of free-floating space robot with rigid manipulators and rigid-flexible manipulators[J].
Journal of Astronautics, 2007, 28 (6) : 1510-1514.
) ( 0) 0)
|
| [8] |
HU Q, XU L, ZHANG A. Adaptive backstepping trajectory tracking control of robot manipulator[J].
Journal of the Franklin Institute, 2012, 349 (3) : 1087-1105.
doi: 10.1016/j.jfranklin.2012.01.001 ( 0) 0)
|
| [9] |
谢箭, 刘国良, 颜世佐, 等. 基于神经网络的不确定性空间机器人自适应控制方法研究[J].
宇航学报, 2010, 31 (1) : 123-129.
( XIE J, LIU G L, YAN S Z, et al. Study on neural network adaptive control method for uncertain space manipulator[J].
Journal of Astronautics, 2010, 31 (1) : 123-129.
) ( 0) 0)
|
| [10] |
李世敬, 王解法, 冯祖仁, 等. 基于动态观测器的不确定机器人鲁棒控制研究[J].
兵工学报, 2005, 26 (2) : 263-266.
( LI S J, WAN J F, FENG Z R, et al. A study on the uncertain robust control of robot based on dynamic observe[J].
Acta Armamentarii, 2005, 26 (2) : 263-266.
) ( 0) 0)
|
| [11] |
DE WIT C C, FIXOT N. Robot control via robust estimated state feedback[J].
Automatic Control, IEEE Transactions on, 1991, 36 (12) : 1497-1501.
doi: 10.1109/9.106170 ( 0) 0)
|
| [12] |
NIU Y, WANG X, HU C. Neural network output feedback control for uncertain robot[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation. Piscataway, NJ: IEEE, 2002: 1980-1984.
( 0) 0)
|
| [13] |
SUN T, PEI H, PAN Y, et al. Neural network-based sliding mode adaptive control for robot manipulators[J].
Neurocomputing, 2011, 74 (14) : 2377-2384.
( 0) 0)
|
| [14] |
谢立敏, 陈力. 输入力矩受限情况下漂浮基空间机械臂的鲁棒自适应混合控制[J].
工程力学, 2013, 30 (3) : 371-376.
( XIE L M, CHEN L. Robust and adaptive composite control of space manipulator system with bounded torque inputs[J].
Engineering Mechanics, 2013, 30 (3) : 371-376.
) ( 0) 0)
|
| [15] |
梁捷, 陈力. 执行器受限空间机器人的模糊神经网络控制[J].
工程力学, 2014, 31 (11) : 190-197.
( LIANG J, CHEN L. Fuzzy neural network control for a space-based robot with constrained actuators[J].
Engineering Mechanics, 2014, 31 (11) : 190-197.
) ( 0) 0)
|
| [16] |
ZHANG Q, MILLS J K, CLEGHORN W L, et al. Trajectory tracking and vibration suppression of a 3-PRR parallel manipulator with flexible links[J].
Multibody System Dynamics, 2015, 33 (1) : 27-60.
doi: 10.1007/s11044-013-9407-2 ( 0) 0)
|
| [17] |
于潇雁, 陈力. 参数不确定与有界干扰自由漂浮柔性空间机械臂基于速度观测器的奇异摄动鲁棒控制及振动抑制[J].
振动与冲击, 2015, 34 (14) : 85-92.
( YU X Y, CHEN L. Velocity observer based singular perturbation robust control and vibration suppression for a free-floating space flexible manipulator with unknow payload parameters and bounded disturbances[J].
Journal of Vibration and Shock, 2015, 34 (14) : 85-92.
) ( 0) 0)
|
| [18] |
杨明, 董晨, 王松艳, 等. 基于有限时间输出反馈的线性扩张状态观测器[J].
自动化学报, 2015, 41 (1) : 59-66.
( YANG M. DONG C, WANG S Y, et al[J].
Acta Automatica Sinica, 2015, 41 (1) : 59-66.
) ( 0) 0)
|
| [19] |
CASTILLO O, MELIN P. Intelligent adaptive model-based control of robotic dynamic systems with a hybrid fuzzy-neural approach[J].
Applied Soft Computing, 2003, 3 (4) : 363-378.
doi: 10.1016/j.asoc.2003.05.007 ( 0) 0)
|
| [20] |
ZHU W, CHEN H, ZHANG Z. A variable structure robot control algorithm with an observer[J].
IEEE Transactions on Robotics and Automation, 1992, 8 (4) : 486-492.
doi: 10.1109/70.149947 ( 0) 0)
|
| [21] |
GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, 2003, 6: 4989-4996.
http://academic.csuohio.edu/cact/ACC03_ISA0030Final.pdf ( 0) 0)
|




