传统的信号采集方法遵循Nyquist采样定律,要求采样频率必须大于等于信号最高频率的2倍才能在采样之后完整地恢复出原始信号。这样必然存在信息的冗余和存储空间的消耗。由文献[1-4]提出的压缩感知(Compressed Sensing,CS)理论指出:如果信号在某一个正交空间具有稀疏性,就能以较低的频率采样该信号,并能以较高概率重建该信号。CS理论将信号采样和压缩合成一步,用远低于Nyquist采样定理的采样频率采集信号。近年来对于重建算法的研究中有一种基于贪婪迭代的匹配追踪算法,贪婪算法是利用一系列的局部优化的单项更新来避免费时的全面搜索。常用的贪婪算法有正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[5]、正则化正交匹配追踪(Regularized Orthogonal Pursuit,ROMP)算法[6]、压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)算法[7]、子空间追踪(Subspace Pursuit,SP)算法[8]、稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法[9]、分段正交匹配追踪(Stage-wise Orthogonal Matching Pursuit,StOMP)算法[10]。ROMP算法每次迭代选择多个相关列,然后通过正则化选择满足的原子集合。CoSaMP算引入了回溯的思想,每次迭代选择多个原子,再剔除部分不相关的原子,有较好的恢复能力。SP算法也是采用回溯的思想,与CoSaMP算法不同的地方是支撑集中原子的个数是K个,这使得SP算法效率更高。但是OMP算法、ROMP算法、CoSaMP算法和SP算法均需要对稀疏度K的准确估计。如果K值估计得不准确,算法重构能力会下降。SAMP算法是在不知道稀疏度的情况下,通过自适应思想调整步长来逐步逼近原始信号,但是这种算法的重构时间很长。StOMP算法分阶段选择原子,通过残差量与观测矩阵中原子的相关系数的大小选择大于设定阈值的原子。StOMP算法通过多次迭代,每次迭代可以向支撑集加入多个原子,可以得到稀疏解,重构时间大幅降低,其缺点是信号重构率低[11]。文献[12]提出分段正则化正交匹配追踪算法,通过从正则化候选集提取出原子实现快速稳定的恢复信号。但是分段正交匹配追踪算法在正则化之后只选择一组能量最大的原子,可能会导致原子的错误选择。本文算法在StOMP算法的基础上,采用正则化思想二次筛选原子,再结合回溯思想,将解的支撑集中的原子重新筛选一次,删除对解的贡献较低的原子,提高算法的重构率;对感知矩阵进行归一化操作,使算法更加简单。
1 压缩感知及重构算法 1.1 压缩感知理论长度为N的一维原始信号x,对其进行压缩采样,得到观测信号y,理论模型[13]为:
| $\mathbf{y=\Phi x}$ | (1) |
其中Φ是M×N 维的观测矩阵。
如果信号x不是稀疏信号,则x可以通过某种变换Ψ进行稀疏表示,即:
| $\mathbf{x}=\mathbf{\Psi \theta }$ | (2) |
θ为该信号在Ψ变换域的稀疏表示。因此有:
| $\mathbf{y}=\mathbf{\Phi \Psi \theta }=\mathbf{A\theta }$ | (3) |
其中AM*N=ΦΨ为传感矩阵。
由于M远小于N,通过式(3)求解θ是一个欠定问题,无法直接由y求解。当信号为稀疏信号,问题转换为求解最小l0范数问题:
| $\begin{align} & \text{min}{{\left\| \mathbf{\theta } \right\|}_{0}} \\ & \text{s}.\text{t}.y=A\theta \\ \end{align}$ | (4) |
然而对式(4)的求解是一个NP-hard问题,Candes等[14]提出约束等距性质 (Restricted Isometry Property,RIP),并指出高斯随机矩阵与大多数的正交基构成的矩阵不相关,高斯矩阵可以以很高的概率满足RIP条件。可以通过求解一个更简单的l1范数问题得到同样的解:
| $\begin{align} & \text{min}{{\left\| \mathbf{\theta } \right\|}_{1}} \\ & \text{s}.\text{t}.y=A\theta \\ \end{align}$ | (5) |
分段正则化正交匹配追踪算法具有自适应选择原子的特点。此算法不需要提前估计信号的稀疏度,所以不会产生由于稀疏度估计不准确造成的错误。信号x在Ψ域为稀疏的,表示为x=Ψθ,θ为稀疏信号。
分段正交匹配追踪算法过程如下:
输入 观测信号yM×1,阶段数s,传感矩阵A。
1) 初始化:残差r0=y,原子索引集${{\Lambda }_{0}}=\varnothing $。
2) 计算残差rt-1与观测矩阵中各原子的内积,即u=〈A,rt-1〉=ATrt-1。
3) 选择u中大于阈值Th的值,将这些值对应的Φ的列序列号j组成集合J0 ,J0 为一个列向量序号集合。更新索引集、支撑集。
4) 求解最小二乘问题求解θ:
| $\mathbf{\theta }=\text{arg}\underset{\mathbf{\theta }}{\mathop{\text{min}}}\,\left\| \mathbf{y}-{{\mathbf{A}}_{t}}{{\mathbf{\theta }}_{t}} \right\|={{\left( \mathbf{A}_{t}^{\text{T}}{{\mathbf{A}}_{t}} \right)}^{-1}}\mathbf{A}_{t}^{\text{T}}\mathbf{y}$ |
5) 更新残差${{\mathbf{r}}_{t}}=\mathbf{y}-{{\mathbf{A}}_{t}}\mathbf{\theta }=\mathbf{y}-{{\left( \mathbf{A}_{t}^{\text{T}}{{\mathbf{A}}_{t}} \right)}^{-1}}\mathbf{A}_{t}^{\text{T}}\mathbf{y}$。
6) 如果rs≤ε,则停止迭代,否则令t=t+1,判断是否达到初始设定的阶段数s,若达到,停止迭代;若未达到则返回第2)步,继续迭代。
输出 重构信号估计值x=Ψθ。
注:门限$Th={{\sigma }_{s}}{{t}_{s}},2\le {{t}_{s}}\le 3,{{\sigma }_{s}}=\frac{{{\left\| {{\mathbf{r}}_{s}} \right\|}_{2}}}{\sqrt{M}}$。
1.3 改进的StOMP算法由于A的列可能不是单位的l2范数,对矩阵A进行归一化$\mathbf{\tilde{A}=AW}$,其中W是主对角元素是$1/\left\| {{a}_{i}} \right\|,\mathbf{W=}\text{diag(}{{\mathbf{A}}^{\text{T}}}\mathbf{A}{{\text{)}}^{-1}}$。
文献[15]指出,不论使用原始矩阵A还是归一化形式来$\mathbf{\tilde{A}}$计算,贪婪算法都会产生相同的解的支撑集。所以使用归一化矩阵的残差表示为:
| ${{\mathbf{\tilde{r}}}^{k}}=\mathbf{y}-{{\mathbf{\tilde{A}}}_{t}}\mathbf{\hat{\theta }}=\mathbf{y}-{{\mathbf{\tilde{A}}}_{t}}{{\left( \mathbf{\tilde{A}}_{t}^{\text{T}}{{{\mathbf{\tilde{A}}}}_{t}} \right)}^{-1}}\mathbf{\tilde{A}}_{t}^{\text{T}}\mathbf{y}$ |
矩阵归一化会影响结果θt,所以必须执行${{\mathbf{\theta }}_{t}}=\mathbf{W}{{\mathbf{\hat{\theta }}}_{t}}$。
StOMP算法是将相关系数大于设定阈值的原子的序列号组成集合J,这个过程可能会导致加入的原子个数太多,为了缩小选择的范围,增加条件的一个方法就是正则化,即|u(i)|≤2|u(j)|,i,j∈J0。采用正则化操作,对原子进行二次筛选,将选出的原子的列序列号组成集合J0。更新索引集和支撑集,利用最小二乘法进行信号估计。根据回溯思想,选取前αL(0<α<1,L为Λt中元素的个数)个较大元素构成新的支撑集,α大小的选择决定重建算法的运行时间和重建效果。
基于此本文提出一种改进算法——回溯正则化分段正交匹配追踪(Backtracking Regularized Stage-wised Orthogonal Matching Pursuit,BR-StOMP)算法。算法流程简述如下:
输入 观测信号yM×1,传感矩阵A满足A=ΦΨ,归一化矩阵$\mathbf{\tilde{A}}=\mathbf{AW}$,阶段数s。
1) 初始化:残差r0=y,原子索引集为空集。
2) 计算残差rt-1与观测矩阵中各原子的内积,即$u={{\mathbf{\tilde{A}}}^{\text{T}}}{{\mathbf{r}}_{t-1}}$。
3) 设定阈值,选择u中大于阈值Th的值,将这些值对应的列序列号j组成集合J。
4) 正则化:寻找子集合J0$\subset $J,J0满足u(i)≤2u(j),其中i,j∈J0。
5) 更新索引集Λt=Λt-1∪J0,更新支撑集Γt=Γt-1∪J0。
6) 求解最小二乘问题求解$\mathbf{\hat{\theta }}$:$\mathbf{\hat{\theta }}=\text{arg}\underset{\mathbf{\theta }}{\mathop{\text{min}}}\,\left\| \mathbf{y}-{{{\mathbf{\tilde{A}}}}_{t}}{{\mathbf{\theta }}_{t}} \right\|={{\left( \mathbf{\tilde{A}}_{t}^{\text{T}}{{\mathbf{A}}_{t}} \right)}^{-1}}\mathbf{\tilde{A}}_{t}^{\text{T}}\mathbf{y}$。
7) 回溯更新支撑集:根据回溯思想,选取前aL(0<a<1,L 为Λt中元素的个数)个较大元素构成新的支撑集。
8) 更新残差${{\mathbf{\hat{r}}}_{t}}=\mathbf{y}-{{\mathbf{\tilde{A}}}_{t}}\mathbf{\hat{\theta }}=\mathbf{y}-{{\mathbf{\tilde{A}}}_{t}}{{\left( \mathbf{\tilde{A}}_{t}^{\text{T}}{{{\mathbf{\tilde{A}}}}_{t}} \right)}^{-1}}\mathbf{\tilde{A}}_{t}^{\text{T}}\mathbf{y}$。
9) 首先判断${{\left\| {{{\mathbf{\hat{r}}}}_{t}} \right\|}_{2}}\le {{\left\| {{{\mathbf{\hat{r}}}}_{t-1}} \right\|}_{2}}$是否成立,如果成立则停止迭代;如果不成立,则判断是否达到初始设定的阶段数s,若达到,停止迭代。若未达到返回第2)步,继续迭代。
输出 重构信号估计值=ΨW。
2 实验结果及分析为了验证本文算法的性能,本文分别对一维稀疏信号和二维图像进行重构实验。
实验一 对长度为256的高斯随机信号在不同稀疏度下信号进行重构仿真,测量矩阵为高斯随机矩阵。观察α的取值不同对重建信号质量以及运行时间的影响。
1) 不同的稀疏度下,测量值与信号重建恢复率的关系。
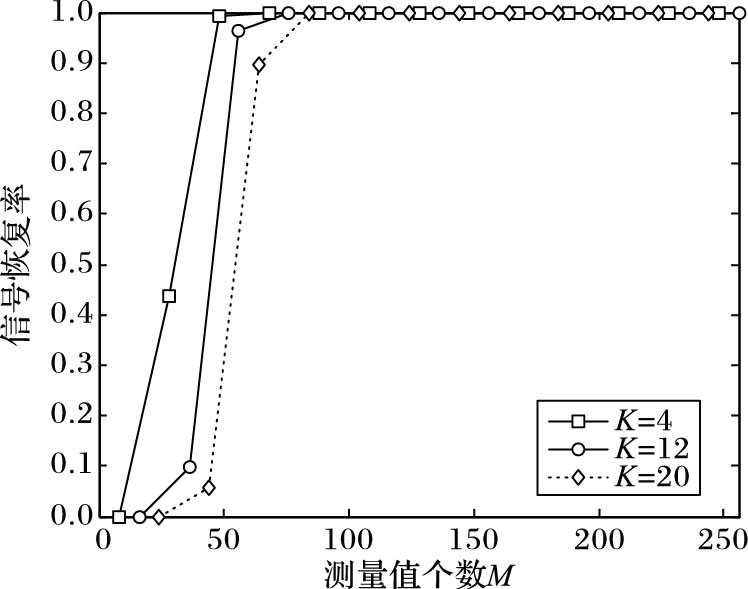
由图 1可见,稀疏度低时,用较低的测量数可以恢复出原始信号,而稀疏度较高时,较低的测量数信号的恢复率比较低。当测量数达到100以上,信号的恢复率近似100%。
|
图 1 信号恢复率与测量值个数之间的关系 |
2) K不同时,α的取值分别为0.5、0.6、0.7、0.8、0.9、1.0时,观察算法对信号的重构误差和重构时间的影响,由1)可知,当测量值取128,采样率对重建效果的影响可以忽略。
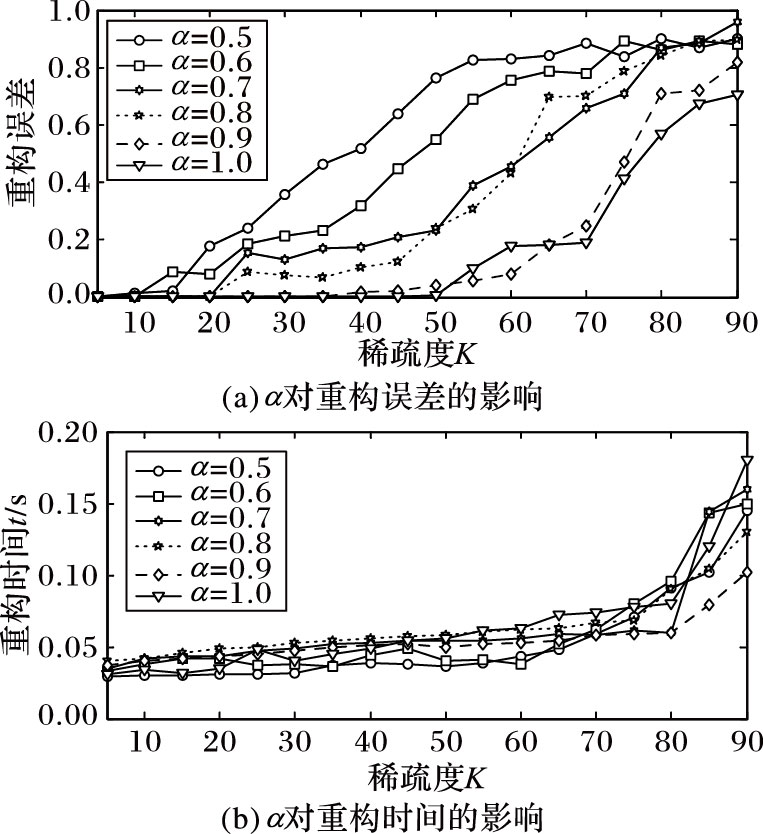
从图 2(a)可以看出,α取值0.5~0.8时,当稀疏度K 小于10,算法对信号的重构误差比较小,随着稀疏度K的增大,重构误差逐渐增大;α取0.9或者1.0,当稀疏度K小于50时,重构误差较小,当K大于50时,重构误差较大,且随着K的增大,呈递增趋势。
|
图 2 不同稀疏度下,α值对重构的影响 |
从图 2(b)的整体趋势看,随着稀疏度的增大,重构时间逐渐增大;同一稀疏度下,α越大运行时间越长。综合考虑α对时间和重建误差的影响,α取值0.9或1.0比较合适。
实验二 对像素大小为256*256的Lena.bmp灰度图进行仿真,图像稀疏采用小波变换,从峰值信噪比判别图像恢复效果。重构错误率$e={\left| \tilde{x}-x \right|}/{\left| x \right|}\;$,α=0.9。
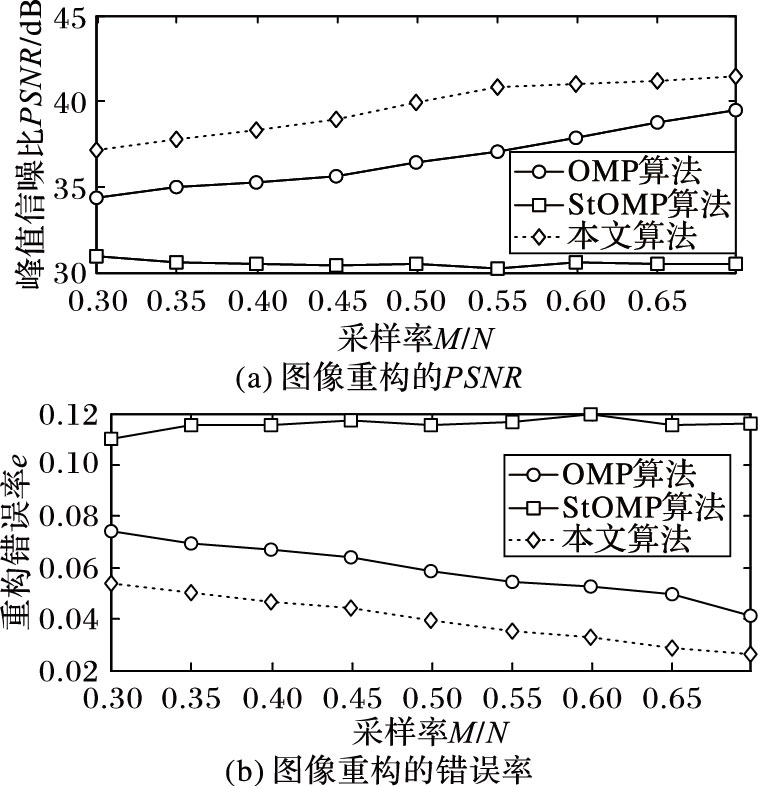
从图 3(a)可以看出,在不同的采样率下,本文算法的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)比StOMP算法提高19%~35%,比OMP算法提高8%~10%。在相同的采样率下,本文算法重构图像的峰值信噪比比其他两种算法大,且随着采样率的增大,呈现递增趋势。
|
图 3 不同采样率下不同算法对图像重构的影响 |
图 3(b)表明随着采样率的增加,StOMP算法的重构错误率保持稳定,本文算法对图像的重构的错误率逐渐降低,且在同一采样率下比OMP算法和StOMP算法的重构错误率都低。
图 4为原始图像以及采样率为0.5时OMP算法、StOMP算法、本文算法对原始图像恢复的效果图。从视觉效果上看本文算法的恢复效果比StOMP算法好。

|
图 4 采样率为0.5时不同算法的重构图像 |
表 1是三种算法在不同的采样率下恢复图像的时间。采用公式β=|tBR-StOMP-tOMP/StOMP|/tOMP/StOMP来计算本文算法与其他两种算法相对时间差比例。
| 表 1 三种算法在不同的采样率下重建图像运行时间 |
从表 1中可以看出,随着采样率的增加,三种算法的运行时间不断增加,其中本文算法的重构时间比StOMP算法多40%~50%,比OMP算法少70%~80%。在初步选择原子过程中一次迭代选择多个原子以及对观测矩阵进行归一化是本文算法和StOMP算法相对OMP算法用时少的原因;回溯操作对原子的重新选择造成本文算法比StOMP算法用时多。
3 结语本文在分段正交匹配追踪算法研究的基础上,将归一化思想、正则化思想以及回溯思想相结合,提出回溯正则化分段正交匹配追踪(BR-StOMP)算法。该算法通过对传感矩阵进行归一化处理使算法运算更加简单;由于在选择相关系数大于阈值的原子过程中,可能加入过多的原子,因此采用正则化操作对原子进行二次筛选,再根据回溯思想对原子进行检验。BR-StOMP算法的重构性能明显优于OMP算法和StOMP算法,重构效率高于OMP算法,是一种兼顾了重构性能和运算效率的一种算法。本文的后续改进工作是研究在相同的采样率下,如何进一步减少算法耗时。
| [1] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52 (4) : 1289-1306. doi: 10.1109/TIT.2006.871582 |
| [2] | CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25 (2) : 21-30. doi: 10.1109/MSP.2007.914731 |
| [3] | 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34 (3) : 425-434. ( DAI Q H, FU C J, JI X Y. Research on compressed sensing[J]. Chinese Journal of Computers, 2011, 34 (3) : 425-434. doi: 10.3724/SP.J.1016.2011.00425 ) |
| [4] | 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37 (5) : 1070-1081. ( SHI G M, LIU D H, GAO D H, et al. Advances in theory and application of compressed sensing[J]. Acta Electronoca Sinica, 2009, 37 (5) : 1070-1081. ) |
| [5] | TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53 (12) : 4655-4666. doi: 10.1109/TIT.2007.909108 |
| [6] | NEEDELL D, VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4 (2) : 310-316. doi: 10.1109/JSTSP.2010.2042412 |
| [7] | NEEDELL D, TROPP J A. CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computation Harmonic Analysis, 2009, 26 (3) : 301-321. doi: 10.1016/j.acha.2008.07.002 |
| [8] | DAI W, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55 (5) : 2230-2249. doi: 10.1109/TIT.2009.2016006 |
| [9] | DO T T, GAN L, NGUYEN N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Proceedings of the 200842nd Asilomar Conference on Signals, Systems, and Computers. Piscataway, NJ:IEEE, 2008:581-587. |
| [10] | DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined linear equations by stage-wise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58 (2) : 1094-1121. doi: 10.1109/TIT.2011.2173241 |
| [11] | 方红, 杨海蓉. 贪婪算法与压缩感知理论[J]. 自动化学报, 2011, 37 (12) : 1413-1421. ( FANG H, YANG H R. Greedy algorithm and compressed sensing[J]. Acta Automatica Sinica, 2011, 37 (12) : 1413-1421. ) |
| [12] | 吴迪, 王奎民, 赵玉新, 等. 分段正则化正交匹配追踪算法[J]. 光学精密工程, 2014, 22 (5) : 1395-1402. ( WU D, WANG K M, ZHAO Y X, et al. Stagewise regularized orthogonal matching pursuit algorithm[J]. Optics and Precision Engineering, 2014, 22 (5) : 1395-1402. doi: 10.3788/OPE. ) |
| [13] | BARANIUK R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 4 (24) : 118-121. |
| [14] | CANDES E, ROMBERG J, TAO T. Stable signal recovery from incomplete and inaccurate measurement[J]. Communication on Pure and Applied Mathematics, 2006, 59 (8) : 1207-1233. doi: 10.1002/(ISSN)1097-0312 |
| [15] | ELAD M. Sparse and Redundant Representations from Theory to Application in Signal and Image Processing[M]. Beijing: National Defense Industry Press, 2015 : 33 -35. |




