2. 火箭军工程大学 信息工程系, 西安 710025 ;
3. 中国人民解放军96261部队, 河南 灵宝 471700
2. Department of Information Engineering, Rocket Force University of Engineering, Xi'an Shaanxi 710025, China ;
3. 96261 Unit of PLA, Lingbao Henan 471700, China
LI Junshan, born in 1956, Ph.D., professor. His research interests include fault diagnosis and maintenance support technology, image processing, computer vision.
TONG Qi, born in 1988, M.S., assistant engineer. His research interests include electronic equipment fault diagnosis.
YE Xia, born in 1977, Ph.D., associate professor. Her research interests include command and information system, network security.
XU Yuan, born in 1986, M.S., assistant. His research interests include intelligent detection.
模拟电路在航空航天、电子对抗、军事防御等领域的设备中发挥着至关重要的作用,其运行状态严重影响着设备的性能和功能,因此研究模拟电路的状态发展趋势,预测元器件剩余寿命,评估电路健康状况,从而确保电路长时间正常稳定工作具有重要意义。
健康度[1]可以用来量化表征元器件性能,通过对健康度变化的时间序列进行预测, 评估元器件工作状态和剩余寿命[2]。在实际应用中,由于模拟电路构成复杂,各元器件相互耦合,加之电气噪声的影响,必然导致所计算的健康度数值序列具有非线性变化的特点,在出现故障或异常后,这一特点表现更为明显。因此,基于健康度的模拟电路状态预测需要解决非线性序列预测问题。
支持向量回归(Support Vector Regression,SVR)是一种将支持向量机(Support Vector Machine, SVM)方法推广应用于时间序列函数回归估计的方法,鲁棒性好、推广能力强、具有全局最优解,被广泛应用于非线性时间序列的预测[3-5]中,有利于解决模拟电路的状态趋势预测问题。根据输入样本的不同,可以将时间序列的SVR预测分为单步预测和多步预测两种[6]。多步预测能得到更加超前的预测结果,比单步预测更具实际意义,但由于误差的存在并不断累积,多步预测的精度会随预测步数的增大而逐渐下降,甚至可能不再反映待预测序列的变化趋势。
针对SVR多步预测的误差累积问题,本文提出了一种基于相空间重构的自适应残差修正SVR预测算法。首先,将相空间重构技术引入到SVR状态预测中;然后,根据预测误差构造残差序列,并进行二次SVR预测,用于修正原始预测值,从而提高了预测精度;最后,利用数值仿真验证算法降低误差累积的效果,并将其应用于模拟电路的健康度时间预测中。
1 支持向量回归 1.1 ε-支持向量回归设(xi, yi)为训练样本,xi∈Rm、yi∈R(i=1, 2, …, N), 则回归函数为:
| $ f(\mathit{\boldsymbol{x}}) = \langle \mathit{\boldsymbol{w}}, \varphi (\mathit{\boldsymbol{x}})\rangle + b $ | (1) |
式中,w∈Rm是权值,φ(x)是映射函数,b∈R是偏置。
当采用ε -不敏感损失函数作为拟合的损失函数时,回归函数的求解可表示成如下的二次型问题:
| $ Q(\mathit{\boldsymbol{w}}, {\xi _i}, \xi _i^*) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\sum\limits_{i = 1}^N {({\xi _i} + \xi _i^*)} $ | (2) |
| $ \begin{array}{*{20}{c}} {s.t.}&{\left\{ \begin{array}{l} {y_i}-f({\mathit{\boldsymbol{x}}_i})-\varepsilon \le {\xi _i}, i = 1, \cdots, N\\ f({\mathit{\boldsymbol{x}}_i})-{y_i} - \varepsilon \le \xi _i^ *, i = 1, \cdots, N\\ {\xi _i}, \xi _i^ * \ge 0, i = 1, \cdots, N \end{array} \right.} \end{array} $ | (3) |
式中: C是惩罚因子; ξi和ξi*是松弛变量; ε表示不敏感损失参数,ε≥0。
引入Lagrange函数:
| $ \begin{array}{l} L(\mathit{\boldsymbol{w}}, \xi, {\xi ^ * }, \varepsilon, b) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\sum\limits_{i = 1}^N {({\xi _i} + \xi _i^*)}-\\ \begin{array}{*{20}{c}} {}&{}&{}&{\begin{array}{*{20}{c}} {}&{\sum\limits_{i = 1}^N {{\alpha _i}({\xi _i} + \varepsilon-{y_i} + \langle \mathit{\boldsymbol{w}} \cdot \varphi ({\mathit{\boldsymbol{x}}_i})\rangle + b)} } \end{array}} \end{array}\\ \begin{array}{*{20}{c}} {}&{}&{}&{\begin{array}{*{20}{c}} {}&{-\sum\limits_{i = 1}^N {\alpha _i^ * (\xi _i^ * + \varepsilon + {y_i} - \langle \mathit{\boldsymbol{w}} \cdot \varphi ({\mathit{\boldsymbol{x}}_i})\rangle - b)} } \end{array}} \end{array}\\ \begin{array}{*{20}{c}} {}&{}&{}&{\begin{array}{*{20}{c}} {}&{ - \sum\limits_{i = 1}^N {({\eta _i}{\xi _i} + \eta _i^ * \xi _i^ * )} } \end{array}} \end{array} \end{array} $ | (4) |
式中:αi、αi*、ηi、ηi*为Lagrange乘子,均大于等于0。
分别对式(4)中的w、ξi、ξi*、ε和b求偏导,令其等于0,并将结果代入式(4),用核函数K(xi, xj)替代内积〈φ(xi), φ(xj)〉,可得原始问题的对偶问题:
| $ \begin{array}{l} {L_p} =-\varepsilon \sum\limits_{i = 0}^N {(\alpha _i^* + {\alpha _i})} + \sum\limits_{i = 0}^N {{y_i}(\alpha _i^*-{\alpha _i})} \\ \begin{array}{*{20}{c}} {}&{-\frac{1}{2}} \end{array}\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {(\alpha _i^* - {\alpha _i})} } (\alpha _j^* - {\alpha _j})K({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}), \\ \begin{array}{*{20}{c}} {}&{s.t.}&{\sum\limits_{i = 0}^N {(\alpha _i^* - {\alpha _i})} } \end{array} = 0, 0 \le {\alpha _i}, \alpha _i^* \le C \end{array} $ | (5) |
式中,当αi*-αi非零时,对应的训练样本为支持向量。
最终得到ε和C控制的回归函数f(x)为:
| $ f(x) = \sum\limits_{i = 1}^N {({\alpha _i}-\alpha _i^ * )} K(\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_i}) + b $ | (6) |
式中K(x, xi)为核函数,该函数可以在不知非线性变换的具体形式下实现算法的非线性化。研究表明,当缺少非线性时间序列的先验知识(比如,噪声特性等)时,SVR核函数一般选用带有核参数σ的高斯径向基核函数[7-8]:
| $ K(\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_i}) = \exp \left( {\frac{{-{{\left\| {{\mathit{\boldsymbol{x}}_i}-\mathit{\boldsymbol{x}}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)\begin{array}{*{20}{c}} , &\sigma \end{array} > 0 $ | (7) |
为评估SVR回归估计的性能,使用模拟时间序列进行拟合分析,设置一个准周期信号:
| $ \begin{array}{*{20}{c}} {y = 0.4\sin t + 0.3\sin (\sqrt 2 t) + }\\ {0.2\sin (\sqrt 3 t) + 0.1{\rm{N}}(0, 1)} \end{array} $ | (8) |
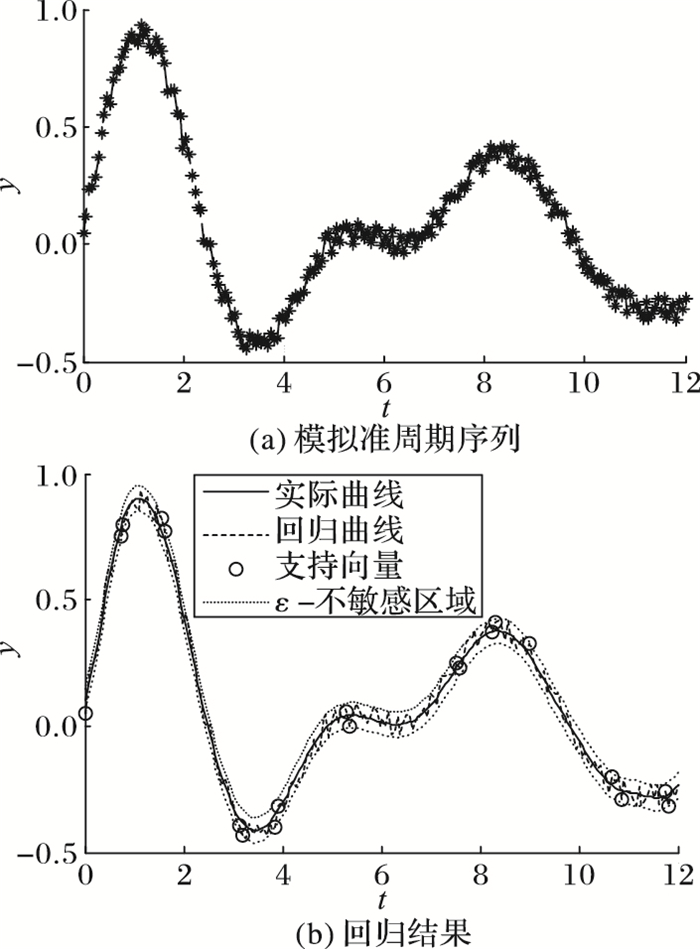
其中,N(0, 1)为该信号包含的正态分布噪声,通过不等距离采样得到100个样本点,如图 1(a)所示。使用高斯径向基核函数和参数对(ε, C, σ)=(0.05, 10, 0.5),经SVR拟合,结果如图 1(b)所示。
|
图 1 SVR回归估计 |
由图 1可以看出,不等距离采样并没有给回归结果带来显著影响,ε-损失带能够将信号的正态分布噪声包含在内,使得回归曲线光滑,并且与准周期信号对应良好。说明SVR回归估计求解得到的是优化问题的全局最优解,只要参数对选取合适,就可以得到较好的回归结果。在参数对(ε, C, σ)中:不敏感损失参数ε反映了模型对数据噪声幅值的容许范围,可通过对噪声进行先验估计而设定。惩罚因子C控制着拟合误差与泛化性能,应根据需要寻找两者之间的折中。核参数σ决定了支持向量数目和模型的复杂程度,σ越小,模型越复杂,回归曲线则相对粗糙;σ越大,支持向量越少,回归曲线越光滑,拟合误差增大。在支持向量回归模型中,惩罚因子C、核参数σ和不敏感损失参数ε共同决定了支持向量回归模型的预测精度和泛化能力[9]。
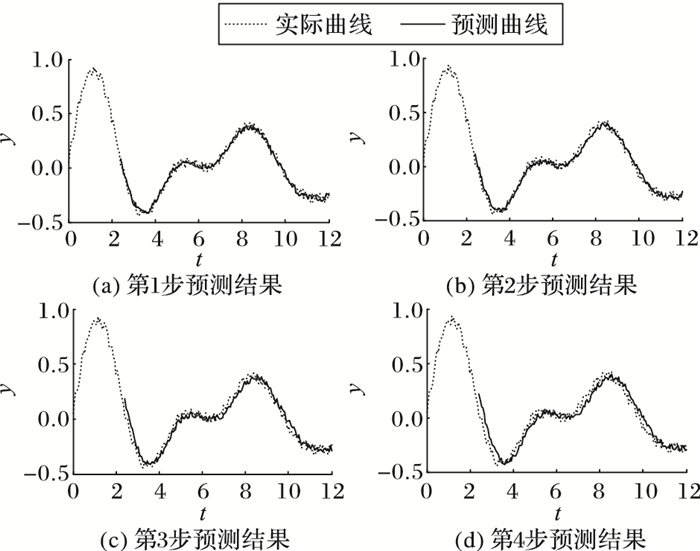
1.3 多步预测的误差累积多步预测将预测值加入模型的输入矢量中,从而得到比单步预测更为超前的预测结果,对时间序列趋势的预测意义更大。对1.2节的准周期信号进行连续多步预测,图 2(a)~图 2(d)分别为第1步~第4步的预测结果。
|
图 2 SVR多步预测结果 |
由图 2可以看出,第1步预测结果与实际曲线最接近,随着预测步数的增大,预测结果逐渐偏离实际曲线,但仍能够较好地反映序列的变化趋势。得到这样的结果是科学合理的,因为多步预测是从单步预测递推得到的,前几步的预测误差会被加入到模型之中,导致误差的累积,使得预测精度降低;但多步预测重在体现序列整体信息,反映样本发展趋势,得到更加超前的预测结果,其意义远远大于单步预测。然而,如果多步预测的偏差过大,甚至超出了序列的承受范围,多步预测便失去了意义,因此需要寻找削减预测误差的方法,以提高多步预测的精度。
2 相空间重构的自适应残差修正SVR预测为解决SVR多步预测存在的误差累积问题,本文提出一种基于相空间重构的自适应残差修正SVR预测算法。将相空间重构技术引入到SVR状态预测中,对多步预测过程中产生的误差累积序列进行二次SVR预测,实现对初始预测误差的自适应修正。
2.1 相空间重构技术相空间重构[10]的基本思想是:在动力学系统中,对于任一系统分量的变化会受到与之相互作用分量的影响。
设单变量时间序列为{x(ti), i=1, 2, …, N},N是序列长度。其重构相空间为:
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}_i}(t) = (x({t_i}), x({t_{i + \tau }}), \cdots, x({t_{i + (m-1)\tau }}))\\ \begin{array}{*{20}{c}} {}&{}&{i = 1, 2, \cdots, N-(m-1)\tau } \end{array} \end{array} $ | (9) |
式中:τ为时间延迟;m为嵌入维数;在重构相空间中,参数τ和m的选择会影响系统的动力学特性,下面分别进行介绍。
2.1.1 时间延迟τ的求解时间延迟τ的求解方法有很多,但互信息法[11]能够获取时间序列的非线性特性,与其他方法相比,其计算结果更优。
若设时间序列为{x(t1), x(t2), …, x(tN)},延迟时间为τ,则相对应的时间序列为{xi+τ, i=1, 2, …, N},xk在序列{xi, i=1, 2, …, N}中出现的概率为p(xk),xk+τ在序列{xi+τ, i=1, 2, …, N}中出现的概率为p(xk+τ),xk和xk+τ在两序列共同出现的联合概率为p(xk, xk+τ)。p(xk)和p(xk+τ)可通过出现频率计算得到,经(xk, xk+τ)可计算得到p(xk, xk+τ),互信息函数即为:
| $ I(\tau ) = \sum\limits_{k = 1}^N {p({x_k}, {x_{k + \tau }})In\frac{{p({x_k}, {x_{k + \tau }})}}{{p({x_k})p({x_{k + \tau }})}}} $ | (10) |
时间延迟τ即为I(τ)的第一个极小值,重构时是使用I(τ)的第一个极小值作为最优延迟时间的。
2.1.2 嵌入维数m的求解求解嵌入维数的常用方法有奇异值分解法、关联指数饱和法、虚假邻域法等。其中,虚假邻域法应用最为广泛,但当噪声存在时效果较差,Cao等提出了改进方法,称为Cao方法[12]。定义为:
| $ a(i, m) = \frac{{\left\| {{\mathit{\boldsymbol{X}}_i}(m + 1)-{\mathit{\boldsymbol{X}}_{n(i, m)}}(m + 1)} \right\|}}{{\left\| {\mathit{\boldsymbol{X}}(m)-{\mathit{\boldsymbol{X}}_{n(i, m)}}(m)} \right\|}} $ | (11) |
式中: i=1, 2, …, N-mτ;Xi(m+1)是m+1维重构相空间的第i个向量;a(i, m), 1≤a(i, m)≤N-mτ使得Xn(i, m)(m)和Xi(m)在m维重构相空间中成为最近邻域整数。对于所有a(i, m)的平均值为:
| $ E(m) = \frac{1}{{N-m\tau }}\sum\limits_{i = 1}^{N-m\tau } {a(i, m)} $ | (12) |
E(m)实际上是一个期望值,然后将m到m+1维的变化定义为:
| $ F(m) = E(m + 1)/E(m) $ | (13) |
如果时间序列是确定的,则维数m存在;当F(m)随着m值慢慢变的饱和时,终止时的m值加1就是最小嵌入维数。
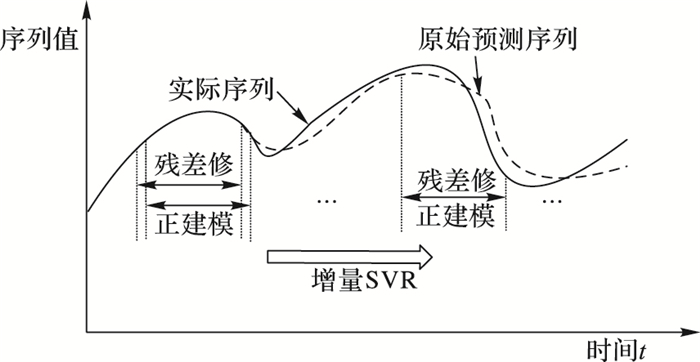
2.2 本文算法利用SVR算法对时间序列进行预测估计,不论是单步预测还是多步预测,其预测值与实际值都可能存在一定的偏差,在连续多次预测之后,这些偏差值也是一个时间序列,称之为残差序列,记作var。通过对残差序列var再进行SVR预测,然后修正原始预测值,就可得到更精确的预测结果,这就是本文提出的基于相空间重构的自适应残差修正SVR预测算法的基本思路,如图 3所示。
|
图 3 自适应残差修正SVR预测算法示意图 |
从图 3可以看出,自适应残差修正SVR预测是在传统SVR预测的基础上,对模型前期预测值与实际值之间的差值序列进行残差SVR建模,然后预测后续预测值与实际值的残差,自适应修正原始预测值,使得预测值与实际值之间的偏差减小。
基于相空间重构的自适应残差修正SVR预测算法的具体实现步骤如下:
步骤1 构造能够反映模拟电路状态单变量的时间序列。
步骤2 选择时间延迟τ和最小嵌入维数m,根据式(9)对时间序列进行相空间重构;其中,当前输入矢量为Xi=(xi, xi+τ, …, xi+(m-1)τ),输出为Yi=xi+mτ(i=1, 2, …, Nm, τ),Nm, τ是输入矢量总数。
步骤3 选择组合参数(ε, C, σ),用前Ntr个数据对,即(Xi, Yi)|i=1, 2, …, Ntr,训练标准SVR模型。
步骤4 利用上述模型根据新输入矢量Xi,对Yi进行预测得到
步骤5 计算当前输入矢量Xi的前Nres个预测值的残差序列
步骤6 对残差序列进行相空间重构,然后利用增量SVR建模预测残差,记为
步骤7 修正预测结果
步骤8 将预测得到的
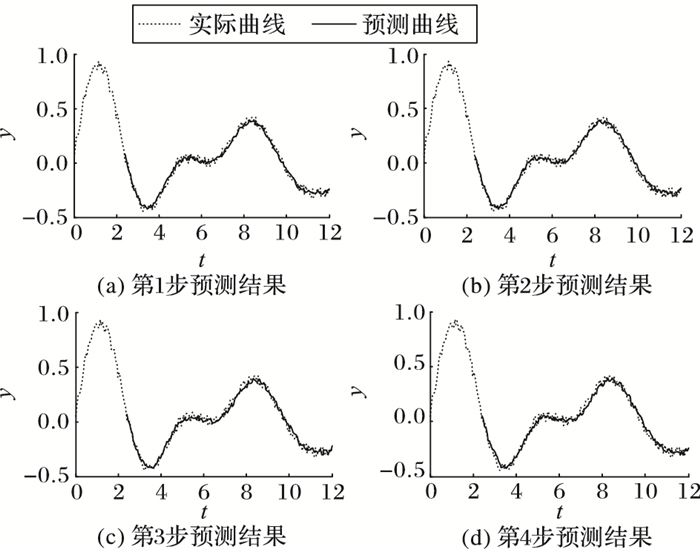
利用基于相空间重构的自适应残差修正SVR预测算法对1.2节的准周期信号进行连续多步预测,时间延迟τ=1,最小嵌入维数m=5,同样使用高斯径向基核函数,相同的参数对(ε, C, σ)=(0.05, 10, 0.5),图 4(a)~图 4(d)分别为第1步~第4步的预测结果。
|
图 4 自适应残差修正SVR多步预测结果 |
对比图 2和图 4可知:在图 2的SVR多步预测结果中,第1步预测结果与实际曲线比较接近,但随着预测步数的增加,预测结果逐渐偏离实际曲线。但在图 4的本文提出的自适应残差修正SVR多步预测结果中,不仅第1步预测结果与实际曲线比较接近,而且随着预测步数的增加,以后各步的预测结果也没有偏离实际曲线的倾向,预测结果也与实际曲线比较接近。说明本文提出的自适应残差修正SVR预测算法能够有效降低预测误差,提高回归估计精度,同时很好地反映序列的变化趋势。表 1列出了两种SVR算法的误差评价指标[7]的对比值,进一步展现了本文算法的优势,从数值量化角度说明了算法减小预报误差的效果。
| 表 1 两种SVR各步的误差评价指标对比 |
为表征模拟电路元器件的性能,本文使用皮尔逊相关系数法(Pearson Product-Moment Correlation Coefficient,PPMCC)处理所提取的特征数据[13],得到量化的健康度数值。健康度可以在一定程度上反映出元器件的某些性能,通过健康度变化的时间序列来推断预测元器件的工作状态和剩余寿命。利用PPMCC计算健康度的公式为:
| $ r(\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{y}}_i}) = \frac{{\sum\limits_{j = 1}^N {({x_j}-\bar x)} ({y_{ij}}-{{\bar y}_i})}}{{\sqrt {\sum\limits_{j = 1}^N {{{({x_j}-\bar x)}^2}\sum\limits_{j = 1}^n {{{({y_{ij}} - {{\bar y}_i})}^2}} } } }} $ | (14) |
其中:x表示参数值与标称值相等时的特征向量; yi表示第i级健康度被提取的特征量(i=1, 2, …, N); N表示健康度的总数; x和yi分别是xjxj和yij的算术平均值。
PPMCC与其他距离度量方式相比,无需对特征量进行预处理,可直接计算健康度,步骤简单,对实现模拟电路故障预测非常有利。若元器件无故障,参数值与标称值相等,则PPMCC的值为1,即元器件健康度也为1;反之,参数值偏离标称值,健康度会慢慢降低。
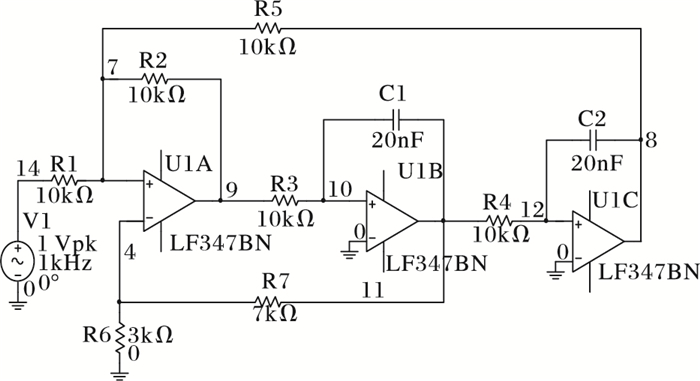
下面以如图 5所示的ITC97国际标准电路中的CTSV(Continuous-Time State-Variable)滤波器电路为例,验证本文所提出的模拟电路故障预测算法在实际应用中的效果。
|
图 5 CTSV滤波器电路 |
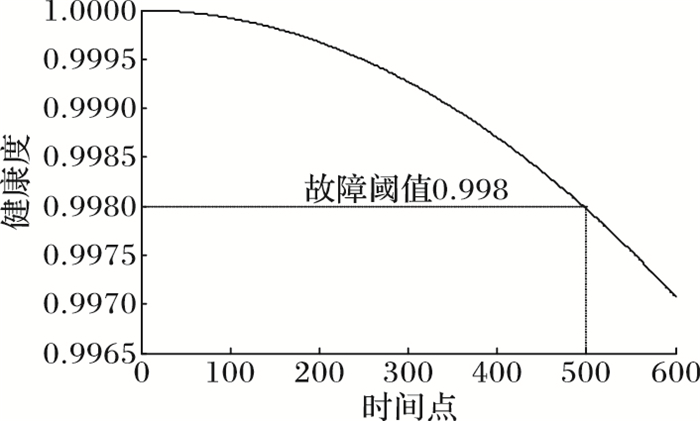
各元器件的标称值均已在图中标出,其中电阻的容差范围为5%,电容的容差范围为10%。通过对电路进行灵敏度分析,发现R3的灵敏度相对较高,因此选择R3作为实验对象。设R3性能退化过程是均匀变化的,且每变化一次就对应一个时间点,R3从10 kΩ增加到16 kΩ,每次增加10 Ω,则共有600个时间点。当元器件参数值偏离标称值50%时,通常可认为该元器件发生故障,因此R3发生故障时的参数值为15 kΩ,经计算可知,第500个时间点即为R3故障发生的时间。
电路输入节点为14,起始频率和截止频率分别设置为1 Hz和10 kHz,节点8为输出测试点。根据提取的电路频率响应信号,利用式(14)计算出R3在各时间点的健康度,轨迹如图 6所示。
|
图 6 R3的健康度轨迹 |
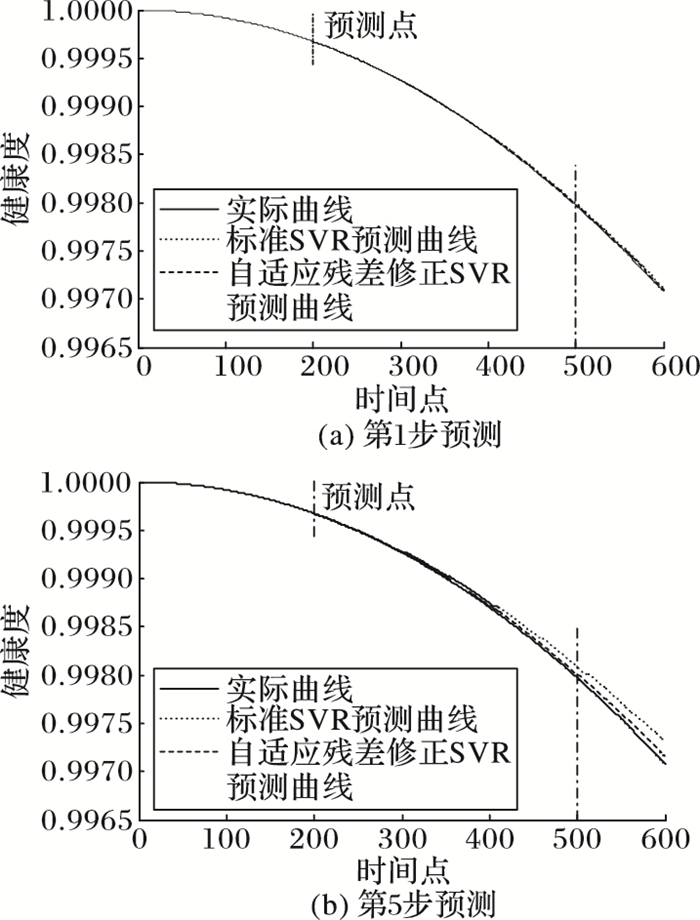
选取R3的前200个时间点的样本数据作为训练数据,剩余的时间点数据为测试数据以验证所提算法的预测能力。分别利用基于相空间重构的自适应残差修正SVR预测算法和传统SVR算法对R3健康度轨迹进行预测,时间延迟τ=1,最小嵌入维数m=5,参数对(ε, C, σ)=(0.05, 10, 0.5),使用同样的高斯径向基核函数,第1步预测和第5步预测结果如图 7所示。
|
图 7 R3-200仿真实验的预测结果 |
从图 7中的预测轨迹可以看出,本文所提SVR算法的预测结果与R3的实际健康度变化曲线非常接近,回归误差小。两种SVR算法对健康度轨迹的第1步预测误差和第5步预测误差如表 2所示。
| 表 2 两种SVR的第1步和第5步预测误差 |
由表 2可知,无论是第1步还是第5步,本文的SVR预测算法的绝对误差均值和相对误差均值都小于传统SVR算法的值;传统SVR算法第5步预测结果的的绝对误差均值相对第1步的值增加了66.3%,而本文的SVR预测算法第5步预测结果的绝对误差均值相对第1步的值只增加了5.7%,绝对误差均值降低了60.5%,说明本文的SVR算法的预测精度较传统SVR算法的预测精度有较大的提升。综上结果可以看出,无论是第1步的预测结果还是第5步的预测结果,本文所提出的SVR预测算法较传统SVR算法的预测精度都要高,更好地反映了健康度轨迹变化趋势。同时,本文算法在第1步预测和第5步预测的效果都较为理想,而传统SVR算法虽然在第1步预测有很好的效果,但多步预测能力明显低于本文所提出的SVR预测算法,这说明本文算法对故障元器件的预测更为精确,有效降低了预测误差,在模拟电路故障预测中具有很好的应用潜力。
4 结语针对模拟电路故障预测存在一定的非线性时间序列预测问题,研究了基于SVR的电路故障预测技术,提出了一种基于相空间重构的自适应残差修正SVR预测算法。将相空间重构技术引入到SVR状态预测中,通过对残差序列var进行SVR预测,修正原始预测值,削减了多步预测的误差累积,从而得到更精确的预测结果。通过仿真实验验证了本文提出的新SVR预测算法能有效降低预测误差,提高回归估计精度,同时很好地反映了序列的变化趋势。将本文算法应用于模拟电路健康度预测中的实验结果可以看出,与传统SVR算法相比本文所提出的新SVR预测算法的多步预测误差累积降低了60%以上,显著提高了预测精度,可有效解决模拟电路状态趋势预测问题。
| [1] | 张朝龙, 何怡刚, 邓芳明, 等. 一种基于QPSO-RVM的模拟电路故障预测方法[J]. 仪器仪表学报, 2014, 35 (8) : 1751-1757. ( ZHANG C L, HE Y G, DENG F M, et al. An approach for analog circuit fault prognostics based on QPSO-RVM[J]. Chinese Journal of Scientific Instrument, 2014, 35 (8) : 1751-1757. ) |
| [2] | 罗慧.模拟电路测试诊断理论与关键技术研究[D].南京:南京航空航天大学, 2012. ( LUO H. Research on testing diagnosis theory and key technology for analog circuits[D]. Nanjing:Nanjing University of Aeronautics & Astronautics, 2012. ) |
| [3] | 张爱华, 王永超, 宋心点, 等. 鲁棒LSSVR的模拟电路性能在线评价策略[J]. 仪器仪表学报, 2013, 34 (10) : 2328-2335. ( ZHANG A H, WANG Y C, SONG X D, et al. Novel online evaluation strategy for analog circuit performance based modified robust LSSVR[J]. Chinese Journal of Scientific Instrument, 2013, 34 (10) : 2328-2335. ) |
| [4] | 王涛, 李艾华, 高运广, 等. 基于相空间重构和遗传优化SVR的机械设备状态趋势预测[J]. 噪声与振动控制, 2014, 34 (3) : 176-181. ( WANG T, LI A H, GAO Y G, et al. Condition trend prediction of mechanical equipments based on phase space reconstruction and genetic optimization support vector regression[J]. Noise and Vibration Control, 2014, 34 (3) : 176-181. ) |
| [5] | LAU K W, WU Q H. Local prediction of non-linear time series using support vector regression[J]. Pattern Recognition, 2008, 41 (5) : 1539-1547. doi: 10.1016/j.patcog.2007.08.013 |
| [6] | 周若愚.基于SVR与半监督学习的时间序列预测[D].西安:西安电子科技大学, 2014. ( ZHOU R Y. Time series prediction based on SVR and semi-supervised learning[D]. Xi'an:Xidian University, 2014. ) http://cdmd.cnki.com.cn/Article/CDMD-10701-1014319524.htm |
| [7] | 陈荣, 梁昌勇, 谢福伟. 基于SVR的非线性时间序列预测方法应用综述[J]. 合肥工业大学学报(自然科学版), 2013, 36 (3) : 369-374. ( CHEN R, LIANG C Y, XIE F W. Application of nonlinear time series forecasting methods based on support vector regression[J]. Journal of Hefei University of Technology (Natural Science), 2013, 36 (3) : 369-374. ) |
| [8] | 李学斯, 毕研刚, 杨宏桥, 等. 一种支持向量回归机自动模型选择方法[J]. 计算机与现代化, 2011 (10) : 19-23. ( LI X S, BI Y G, YANG H Q, et al. An automatic model selection method for support vector regression[J]. Computer and Modernization, 2011 (10) : 19-23. ) |
| [9] | 杨斌.基于EEMD-SVR的预测模型与应用[D].广州:华南理工大学, 2013. ( YANG B. Research of prediction and application based on EEMD-SVR model[D]. Guangzhou:South China University of Technology, 2013. ) http://cdmd.cnki.com.cn/Article/CDMD-10561-1013320129.htm |
| [10] | PACKARD N H, CRUTCHFIELD J P, FARMER J D, et al. Geometry from a time series[J]. Physical Review Letters, 1980, 43 (9) : 712-715. |
| [11] | FARASER A M, SWINNEY H L. Independent coordinates for strange attractors from mutual information[J]. Physical Review A, 1986, 33 (2) : 1134-1140. doi: 10.1103/PhysRevA.33.1134 |
| [12] | CAO L Y, MEE A, JUDD K. Dynamics from multivariate time series[J]. Physica D, 1998, 121 (1) : 75-88. |
| [13] | DERRICK T R, BATES B T, DUFEK J S. Evaluation of time-series data sets using the pearson product-moment correlation coefficient[J]. Medicine and Science in Sports and Exercise, 1994, 26 (7) : 19-28. |




