Visually smooth Gregory patches interpolation of triangle mesh surface model
0 引言
由于三维扫描仪的推广以及计算机处理能力的提升,三角网格模型已经成为产品几何表示的主要方式。轻量化的网格模型对于日益兴起的互联网以及移动端的应用程序在快速传播与轻量化存储两方面具有重要意义。网格模型精简后,虽尽可能保持了原有模型的特征,但曲面不再光顺,大幅影响了渲染的视觉效果。不同于传统曲面参数化[1-2],本文利用四次Gregory曲面对给定的稀疏三角网格模型进行了参数化重建[3-6],保证了重建模型的视觉光顺并使顶点处的法曲率变化最小,解决了目前由于法曲率变化不一致而导致的暗点问题,此方法可以支持快速传输或存储稀疏网格模型,显示时则重构成高质量的精细模型。目前对于四条边界的光顺曲面插值存在大量文献[7-11],但对于三角域插值研究不足。现有工作主要集中在利用四边的Bezier曲面[7-10]进行插值,但大部分均存在扭矢不相容问题,而四边曲面无法像三角曲面那样表示任意拓扑结构的模型。亦有学者利用双三次矩形域Gregory曲面片成功插值出G1连续曲面[12-13],该工作也被延伸到三角域,根据边界曲线插值出全局G1连续的曲面[14]。但目前尚无工作对顶点法曲率变化不一致展开研究,所获得的结果模型由于拼接顶点法曲率不一致通常出现渲染的暗点,并在数控加工时,顶点处会出现加工刀具跳跃,从而难以保证所设计的3D模型能够被快速有效地加工[15]。
1 预备知识与问题描述
假定给定的稀疏网格模型标记为M,由一系列三角片集合{Ti}所构成,Ti的边界为三条有向边{E1, E2, E3},Ti的顶点标记为V1、V2与V3。本文先用四次Bezier曲线插值Ti的三条边{E1, E2, E3}为{C1, C2, C3},再根据G1连续以及法曲率差异最小的约束条件生成四次三角域的Gregory曲面,并使其边界为{C1, C2, C3}。最终M模型会重构为M={$\overline {{T_i}} $}。相邻$\overline {{T_i}} $之间保证G1光顺连接,并保证曲面拼接顶点处法曲率差异最小。
1.1 四次三角域的Gregory曲面表示
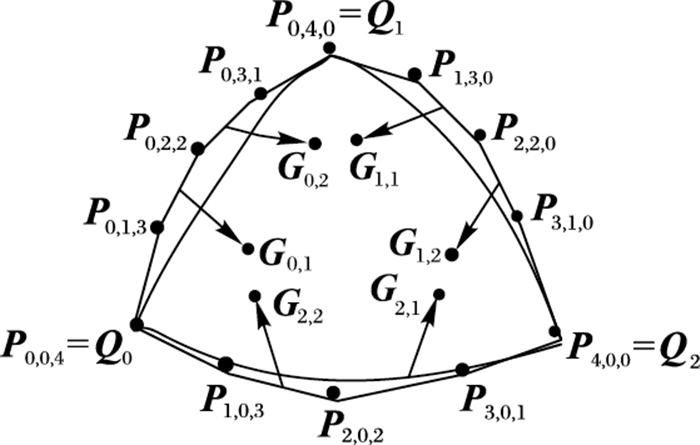
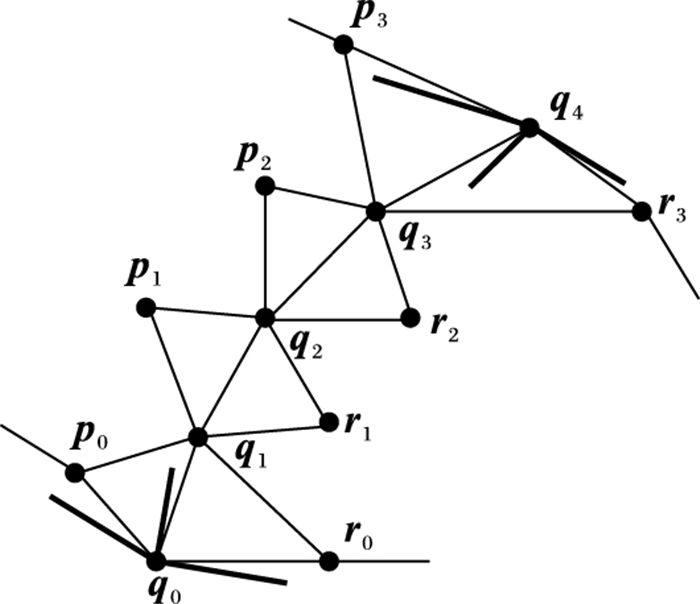
四次三角域的Gregory曲面片可由一组控制点集确定,控制点集如图 1所示,包括:Q={P0, 4, 0, P0, 0, 4, P4, 0, 0, P0, 1, 3, P0, 2, 2, P0, 3, 1, P1, 3, 0, P2, 2, 0, P3, 1, 0, P3, 0, 1, P2, 0, 2, P1, 0, 3, G0, 2, G1, 1, G0, 1, G1, 2, G2, 2, G2, 1},其中P0, 4, 0, P0, 0, 4, P4, 0, 0称作角控制点,为简便描述则分别缩写为Q0、Q1和Q2;P0, 1, 3, P0, 2, 2, P0, 3, 1, P1, 3, 0, P2, 2, 0, P3, 1, 0, P3, 0, 1, P2, 0, 2, P1, 0, 3为边界控制点;G0, 2, G1, 1, G0, 1, G1, 2, G2, 2, G2, 1为内部控制点。四次三角域Bezier的重心参数坐标记为(u, v, w),其参数形式表示为式(1):
|
$
S\left( {u,v,w} \right) = \sum\limits_{i + j + k = 4} {{{\boldsymbol{P}}_{i,j,k}}\frac{{4!}}{{i!j!k!}}} {u^i}{v^j}{w^k}
$
|
(1) |
其中:u, v, w≥0;u+v+w=1;i, j, k≥0。
三角域Gregory曲面片的参数形式和同阶的三角域Bezier曲面片的参数形式相同,边界线为Bezier曲线;唯一差别体现在Gregory曲面的内部控制点P1, 1, 2, P1, 2, 1, P2, 1, 1是动态变化的,它们是关于固定控制点G0, 2, G1, 1, G0, 1, G1, 2, G2, 2, G2, 1与u、v、w参数坐标的函数,表示如下:
|
$
{\boldsymbol{P}_{1,1,2}} = \frac{1}{{u + v}}(u{\boldsymbol{G}_{2,2}} + v{\boldsymbol{G}_{0,1}})
$
|
(2) |
|
$
{\boldsymbol{P}_{1,2,1}} = \frac{1}{{w + u}}\left( {w{\boldsymbol{G}_{0,2}} + u{\boldsymbol{G}_{1,1}}} \right)
$
|
(3) |
|
$
{\boldsymbol{P}_{2,1,1}} = \frac{1}{{v + w}}\left( {v{\boldsymbol{G}_{1,2}} + w{\boldsymbol{G}_{2,1}}} \right)
$
|
(4) |
1.2 三角域Gregory曲面在边界处方向导数
本文涉及到曲面顶点处法曲率的计算,而法曲率的计算需计算曲面片边界处的一阶二阶方向导数,故对n阶Gregroy曲面片的方向导数进行计算。由于Gregory曲面在边界退化为同阶的Bezier曲面,其在边界处的方向导数可采用de Castelijau算法计算[16]。为方便表达,引入标记I,其中|I|=i+ j+ k;让e1=(1, 0, 0), e2=(0, 1, 0), e3=(0, 0, 1)以及重心参数坐标缩写为ϕ=(u, v, w)。定义如下:
|
$
b_{\mathop{\rm I}\nolimits} ^r\left( {\pmb{\mathit{ϕ}}} \right) = ub_{{\mathop{\rm I}\nolimits} + {{\bf{e}}_1}}^{r - 1}\left( {\pmb{\mathit{ϕ}}} \right) + vb_{{\mathop{\rm I}\nolimits} + {{\bf{e}}_{\bf{2}}}}^{r - 1}\left( {\pmb{\mathit{ϕ}}} \right) + wb_{{\mathop{\rm I}\nolimits} + {{\bf{e}}_{\bf{3}}}}^{r - 1}\left( {\pmb{\mathit{ϕ}}} \right)
$
|
(5) |
其中:r=1, 2, …, n; |I|=n-r,并且bI0(ϕ)=bI。
n阶Gregory曲面片在边界,沿着方向L={d, e, f}的方向导数DLb(ϕ)则计算为:
|
$
{D_{L}}b\left( {\pmb{\mathit{ϕ}}} \right) = n\left[ {db_{{{\bf{e}}_1}}^{n - 1}\left( {\pmb{\mathit{ϕ}}} \right) + eb_{{{\bf{e}}_{\bf{2}}}}^{n - 1}\left( {\pmb{\mathit{ϕ}}} \right) + fb_{{{\bf{e}}_{\bf{3}}}}^{n - 1}\left( {\pmb{\mathit{ϕ}}} \right)} \right]
$
|
(6) |
2 边界曲线的插值
2.1 边界曲线的初定
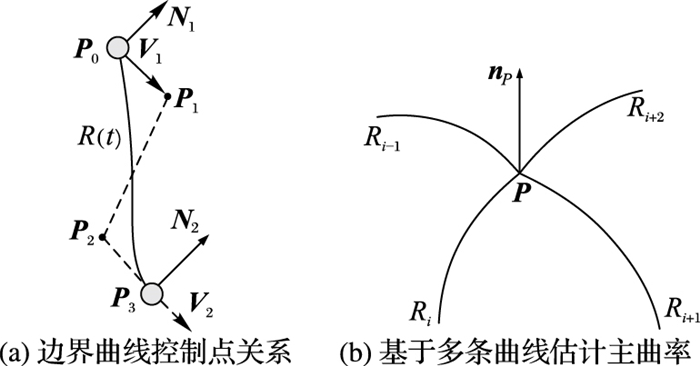
对于给定的Ti,取其任何一条边E1,端点如图 2(a)记为P0与P3。针对该边进行Bezier曲线插值,其余两条边E2和E3均可采用类似方法进行插值。假设P0和P3的顶点法线分别为预设或计算为N1、N2(如没预设则计算为顶点周围三角面的平均面法线)。根据我们之前的方法利用最小能量法[17]对给定两端点以及法线的三次Bezier曲线插值的方法,除已知端点P0和P3,未知两控制点P1和P2计算为:
|
$
\left\{ \begin{array}{l}
{\mathit{\boldsymbol{P}}_1} = {\mathit{\boldsymbol{P}}_0} + \frac{{2\left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{V}}_1}} \right\rangle - \left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{V}}_2}} \right\rangle \left\langle {{\mathit{\boldsymbol{V}}_1},{\mathit{\boldsymbol{V}}_2}} \right\rangle }}{{4 - {{\left\langle {{\mathit{\boldsymbol{V}}_1},{\mathit{\boldsymbol{V}}_2}} \right\rangle }^2}}}{\mathit{\boldsymbol{V}}_1}\\
{\mathit{\boldsymbol{P}}_2} = {\mathit{\boldsymbol{P}}_3} + \frac{{\left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{V}}_1}} \right\rangle \left\langle {{\mathit{\boldsymbol{V}}_1},{\mathit{\boldsymbol{V}}_2}} \right\rangle - 2\left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{V}}_2}} \right\rangle }}{{4 - {{\left\langle {{\mathit{\boldsymbol{V}}_1},{\mathit{\boldsymbol{V}}_2}} \right\rangle }^2}}}{\mathit{\boldsymbol{V}}_2}
\end{array} \right.
$
|
(7) |
其中:
|
$
\left\{ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{V}}_1} = \frac{{{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0} - \left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{N}}_1}} \right\rangle {\mathit{\boldsymbol{N}}_1}}}{{\left\| {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0} - \left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{N}}_1}} \right\rangle {\mathit{\boldsymbol{N}}_1}} \right\|}}}\\
{{\mathit{\boldsymbol{V}}_2} = \frac{{{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0} - \left\langle {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{N}}_2}} \right\rangle {\mathit{\boldsymbol{N}}_2}}}{{\left\| {{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0} - {\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{P}}_0},{\mathit{\boldsymbol{N}}_2}{\mathit{\boldsymbol{N}}_2}} \right\|}}}
\end{array}} \right.
$
|
考虑到插值曲面为4次,则对所求得的Bezier曲线进行一次升阶,其控制点重新计算为:
|
$
{{\mathit{\boldsymbol{\bar P}}}_j} = 1/4[j{\mathit{\boldsymbol{P}}_j}_{ - 1} + \left( {4 - j} \right){\mathit{\boldsymbol{P}}_j}];j = 0, \cdots ,4
$
|
(8) |
2.2 边界曲线的修正
由式(8)获得的四次Bezier曲线在曲面拼接的顶点处,法曲率存在不相容的现象,所以需首先定义拼接顶点的最大最小主法曲率k1和k2以及相应的主曲率方向,然后根据确定的主曲率大小以及方向对由式(8)所获得的曲线进行修正。
2.2.1 顶点主曲率的定义
如图 2(b)所示,设曲线Ri(t)为交汇于顶点P并嵌入曲面S上的正则曲线集[18-19]。${{\dot R}_i}, {{\ddot R}_i}$分别为Ri(t)的一阶和二阶导数,曲面S在P点上的法向为nP,法曲率为knP;曲线Ri(t)在P的法向为niP,曲线曲率则由式(9)进行计算:
|
$
{k_{iP}}{\boldsymbol{n}_{iP}} = \frac{{\left( {{{\dot R}_i} \times {{\ddot R}_i}} \right) \times {{\dot R}_i}}}{{|{{\ddot R}_i}{|^4}}}
$
|
(9) |
根据曲面法曲率的定义,曲面S在P点沿着方向Ṙi(t)的法曲率标记为kniP可计算为:
|
$
{k_{niP}} = {k_{iP}}{\boldsymbol{n}_P} \cdot {\boldsymbol{n}_{iP}} = {k_{iP}}\cos \varphi
$
|
(10) |
其中cos φ=nP·niP。
根据欧拉公式,曲面S在P点沿与切平面x轴夹角为θ方向上的法曲率knP计算为:
|
$
{k_{nP}}(\theta ) = {k_1}{\cos ^2}(\theta - \alpha ) + {k_2}{\sin ^2}(\theta - \alpha )
$
|
(11) |
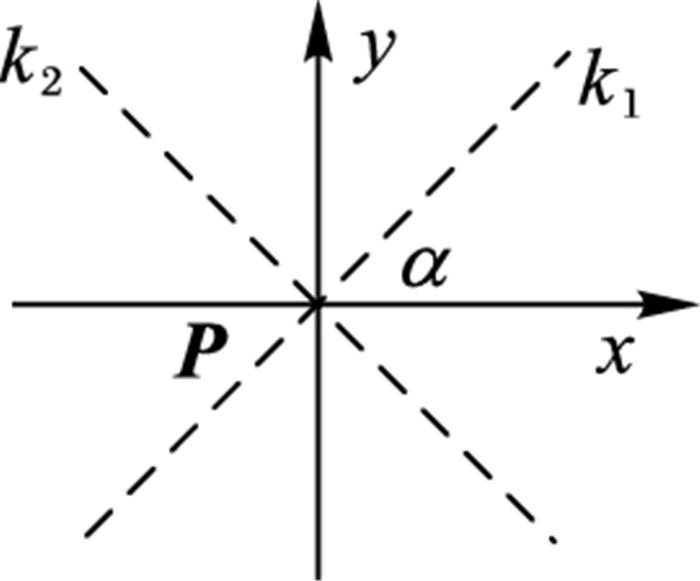
其中α为主曲率方向k1与切平面上x轴之间的夹角(如图 3所示)。切平面x轴可任意指定为其中一条Ri(t)在P点的切线方向即可。
根据式(10),所有Ri(t)可以计算出kniP; 根据式(11)亦可获得kniP,式(12)的差异期望为最小:
|
$
D = {\sum\limits_{i = 1}^m {\left[ {{k_1}{{\cos }^2}\left( {{\theta _i} - \alpha } \right) + {k_2}{{\sin }^2}\left( {{\theta _i} - \alpha } \right) - {k_{niP}}} \right]} ^2}
$
|
(12) |
m为交于该点的曲线数,θi为与x轴的夹角。通过最小二乘使D值最小,可得:
|
$
\tan \alpha = \frac{{\sum\limits_{i = 1}^m {|{k_{niP}}|\sin {\theta _i}\cos {\theta _i}} }}{{\sum\limits_{i = 1}^m {|{k_{niP}}|{{\cos }^2}{\theta _i}} }}
$
|
(13) |
角度α求解出后,D关于k1、k2的偏导数为线性(如式(14)、(15)),令其为零联立方程(14)与(15)可求出k1与k2。
|
$
\begin{array}{c}
\frac{{\partial D}}{{\partial {k_1}}} = 2{k_2}\sum\limits_{i = 0}^m {{{\sin }^2}} \left( {{\theta _i} - \alpha } \right){\cos ^2}\left( {{\theta _i} - \alpha } \right) + \\
2{k_1}\sum\limits_{i = 0}^m {{{\cos }^4}} \left( {{\theta _i} - \alpha } \right) - 2\sum\limits_{i = 0}^m {{k_{niP}}{{\cos }^2}\left( {{\theta _i} - \alpha } \right) = 0}
\end{array}
$
|
(14) |
|
$
\begin{array}{c}
\frac{{\partial D}}{{\partial {k_2}}} = 2{k_1}\sum\limits_{i = 0}^m {{{\sin }^2}} \left( {{\theta _i} - \alpha } \right){\cos ^2}\left( {{\theta _i} - \alpha } \right) + \\
2{k_2}\sum\limits_{i = 0}^m {{{\sin }^4}} \left( {{\theta _i} - \alpha } \right) - 2\sum\limits_{i = 0}^m {{k_{niP}}{{\sin }^2}\left( {{\theta _i} - \alpha } \right) = 0}
\end{array}
$
|
(15) |
2.2.2 基于法曲率修正边界曲线
获得k1, k2以及角度α后,对所有通过(8)所求的4次Bezier曲线进行修正,由于P2的移动不会影响到端点位置以及曲面法线的插值,但可影响到待修正曲线的法曲率值,所以对P2进行修正。设待修正曲线的参数形式为α(t),速率为v,α(t)在点的法曲率标记为knαP,曲线法向标记为nαP,曲面在该点处沿着α(t)切线方向的法曲率标记为knP,曲面法向为nP。曲线α(t)的单位切线与法线记为T和N=nαP。则曲线α(t)的速度和加速度可表示为式(16):
|
$
\left\{ \begin{array}{l}
\dot \alpha \left( t \right) = v\boldsymbol{T}\\
\ddot \alpha \left( t \right) = \frac{{dv}}{{dt}}\boldsymbol{T} + {k_{n\alpha \bar P}}{v^2}\boldsymbol{N}
\end{array} \right.
$
|
(16) |
根据式(9)~(10)可得:
|
$
{k_{n\bar P}} = {k_{n\alpha \bar P}}{n_{\bar P}} \cdot {\boldsymbol{n}_{\alpha \bar P}} = \frac{{v\boldsymbol{T} \times \left( {\frac{{dv}}{{dt}}\boldsymbol{T} + {k_{n\alpha \bar P}}{v^2}\boldsymbol{N}} \right) \times v\boldsymbol{T}}}{{{v^4}}} \cdot {\boldsymbol{n}_{\bar P}}
$
|
(17) |
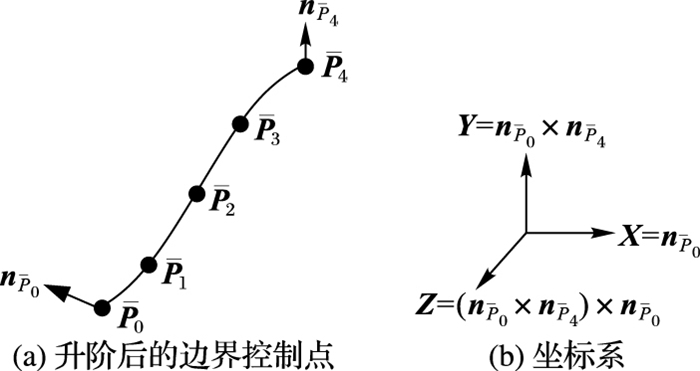
根据以上分析,对2.1节所获四次Bezier边界曲线进行修正:如图 4(a)所示,原有控制点标记为P0、P1、P2、P3、P4;P2修正后记为2,两端点处曲面的法向量分别为nP0, nP4,法曲率为kP0, kP4,速率为vP0, vP4,由式(17)得:
|
$
v_{{{\bar P}_0}}^2{k_{n{{\bar P}_0}}} = 12\left( {{\boldsymbol{{\tilde P}}_2} - 2{\boldsymbol{{\bar P}}_1} + {\boldsymbol{{\bar P}}_0}} \right) \cdot {\boldsymbol{n}_{{{\bar P}_0}}}
$
|
(18) |
|
$
v_{{{\bar P}_4}}^2{k_{n{{\bar P}_4}}} = 12\left( {{\boldsymbol{P}_4} - 2{\boldsymbol{P}_3} + {\boldsymbol{{\tilde P}}_2}} \right) \cdot {\boldsymbol{n}_{{{\bar P}_4}}}
$
|
(19) |
为使P2变化最小,建立约束条件:
|
$
\min {\left\| {{\boldsymbol{{\tilde P}}_2} - {\boldsymbol{{\bar P}}_2}} \right\|^2}
$
|
(20) |
建立如图 4(b)所示坐标系,可得:
|
$
{{\mathit{\boldsymbol{\tilde P}}}_2} = {{\mathit{\boldsymbol{\bar P}}}_2} + a\mathit{\boldsymbol{X}} + b\mathit{\boldsymbol{Y}} + c\mathit{\boldsymbol{Z}}
$
|
(21) |
其中X=nP0, Y=nP0×nP4, Z=(nP0×nP4)×nP0。
由Bezier曲线性质有:
|
$
\left\{ \begin{array}{l}
{v_{{{\mathit{\boldsymbol{\bar P}}}_0}}} = \left| {4\left( {{{\mathit{\boldsymbol{\bar P}}}_1} - {{\mathit{\boldsymbol{\bar P}}}_0}} \right)} \right|\\
{v_{{{\mathit{\boldsymbol{\bar P}}}_4}}} = \left| {4\left( {{{\mathit{\boldsymbol{\bar P}}}_4} - {{\mathit{\boldsymbol{\bar P}}}_3}} \right)} \right|
\end{array} \right.
$
|
(22) |
|
$
\left\{ \begin{array}{l}
{k_{{{\mathit{\boldsymbol{\bar P}}}_0}}} = \frac{{\left| {\left( {{{\mathit{\boldsymbol{\bar P}}}_1} - {{\mathit{\boldsymbol{\bar P}}}_0}} \right) \times \left( {{{\mathit{\boldsymbol{\bar P}}}_2} - 2{{\mathit{\boldsymbol{\bar P}}}_1} + {{\mathit{\boldsymbol{\bar P}}}_0}} \right)} \right|}}{{{{\left| {{{\mathit{\boldsymbol{\bar P}}}_1} - {{\mathit{\boldsymbol{\bar P}}}_0}} \right|}^3}}}\\
{k_{{{\mathit{\boldsymbol{\bar P}}}_4}}} = \frac{{\left| {\left( {{{\mathit{\boldsymbol{\bar P}}}_4} - {{\mathit{\boldsymbol{\bar P}}}_3}} \right) \times \left( {{{\mathit{\boldsymbol{\bar P}}}_4} - 2{{\mathit{\boldsymbol{\bar P}}}_3} + {{\mathit{\boldsymbol{\bar P}}}_2}} \right)} \right|}}{{{{\left| {{{\mathit{\boldsymbol{\bar P}}}_4} - {{\mathit{\boldsymbol{\bar P}}}_3}} \right|}^3}}}
\end{array} \right.
$
|
(23) |
联立式(18)~(21)得:
|
$
a = \frac{1}{{12}}v_{{{\bar P}_0}}^2{k_{{{\bar P}_0}}} - ({{\mathit{\boldsymbol{\bar P}}}_2} - {{\mathit{\boldsymbol{\bar P}}}_1}) \cdot {\mathit{\boldsymbol{n}}_{{{\bar P}_0}}}
$
|
(24) |
|
$
c = \left( {\frac{1}{{12}}v_{{{\bar P}_4}}^2{k_{{{\bar P}_4}}} - \left( {{{\mathit{\boldsymbol{\bar P}}}_2} - {{\mathit{\boldsymbol{\bar P}}}_3}} \right) \cdot {\mathit{\boldsymbol{n}}_{{{\bar P}_4}}} - a\mathit{\boldsymbol{X}} \cdot {\mathit{\boldsymbol{n}}_{{{\bar P}_4}}}} \right)/\left( {\mathit{\boldsymbol{Z}} \cdot {\mathit{\boldsymbol{n}}_{{{\bar P}_4}}}} \right)
$
|
(25) |
且b可以任意取值。
3 法曲率一致的光顺Gregory曲面插值
x(t)为连接两个四次Gregory曲面片公共边界曲线(如图 5, 控制点为qi(i=0, 1, …, 4)),如两曲面片满足G1连续则存在函数λ(t)和μ(t)使得:
|
$
\begin{array}{l}
\left[ {1 - \lambda \left( t \right)} \right]p\left( t \right) + \lambda \left( t \right)r\left( t \right) = \\
\;\;\;\;\;\left[ {1 - \mu \left( t \right)} \right]{q^0}\left( t \right) + \mu \left( t \right){q^n}\left( t \right)
\end{array}
$
|
(26) |
p(t)、q0(t)、qn(t)和r(t)显示表达为:
|
$
\left\{ \begin{array}{l}
p\left( t \right) = \sum\limits_{i = 0}^{n - 1} {{\boldsymbol{p}_i}{B_{i,n - 1}}\left( t \right)} \\
{q^0}\left( t \right) = \sum\limits_{i = 0}^{n - 1} {{\boldsymbol{q}_i}{B_{i,n - 1}}\left( t \right)} \\
{q^n}\left( t \right) = \sum\limits_{i = 0}^{n - 1} {{\boldsymbol{q}_{i + 1}}{B_{i,n - 1}}\left( t \right)} \\
r\left( t \right) = \sum\limits_{i = 0}^{n - 1} {{\boldsymbol{r}_i}{B_{i,n - 1}}\left( t \right)}
\end{array} \right.
$
|
(27) |
其中基函数Bi, n(t)是n次Bernstein多项式,定义为:
|
$
{B_{i,n}}\left( t \right) = \left( {\begin{array}{*{20}{c}}
n\\
i
\end{array}} \right){t^i}{\left( {1 - t} \right)^{n - i}}{\rm{ , }}\left( {0 \le t \le 1} \right)
$
|
为简化考虑,λ(t)、μ(t)构建为一次线性函数如下:
|
$
\left\{ \begin{array}{l}
\lambda \left( t \right) = \left( {1 - t} \right){\lambda _0} + t{\lambda _1}\\
\mu \left( t \right) = \left( {1 - t} \right){\mu _0} + t{\mu _1}
\end{array} \right.
$
|
(28) |
为简化书写,令${\tilde x}$=1-x,式(26)中G1连续条件可化为:
|
$
\begin{array}{l}
\left[ {\left( {1 - t} \right){{\tilde \lambda }_0} + t{{\tilde \lambda }_1}} \right]\sum\limits_{i = 0}^3 {{\boldsymbol{p}_i}{B_{i,3}}\left( t \right)} + \\
\;\;\;\;\left[ {\left( {1 - t} \right){\lambda _0} + t{\lambda _1}} \right]\sum\limits_{i = 0}^3 {{\boldsymbol{r}_i}{B_{i,3}}\left( t \right)} = \\
\;\;\;\;\left[ {\left( {1 - t} \right){{\tilde \mu }_0} + t{{\tilde \mu }_1}} \right]\sum\limits_{i = 0}^3 {{\boldsymbol{q}_i}{B_{i,3}}\left( t \right)} + \\
\;\;\;\;\left[ {\left( {1 - t} \right){\mu _0} + t{\mu _1}} \right]\sum\limits_{i = 0}^3 {{\boldsymbol{q}_{i + 1}}{B_{i,3}}\left( t \right)}
\end{array}
$
|
(29) |
经整理得:
|
$
\begin{array}{l}
\frac{i}{4}\left( {{{\tilde \lambda }_1}{\boldsymbol{p}_{i - 1}} + {\lambda _1}{\boldsymbol{r}_{i - 1}}} \right) + \frac{{4 - i}}{4}\left( {{{\tilde \lambda }_0}{\boldsymbol{p}_i} + {\lambda _0}{\boldsymbol{r}_i}} \right) = \\
\;\;\;\;\;\frac{i}{4}\left( {{{\tilde \mu }_1}{\boldsymbol{q}_{i - 1}} + {\mu _1}{\boldsymbol{q}_i}} \right) + \frac{{4 - i}}{4}\left( {{{\tilde \mu }_0}{\boldsymbol{q}_i} + {\mu _0}{\boldsymbol{q}_{i + 1}}} \right)
\end{array}
$
|
(30) |
分别列出i=0, 1, …, 4,可得5个线性方程:
|
$
{{\tilde \lambda }_0}{\boldsymbol{p}_0} + {\lambda _0}{\boldsymbol{r}_0} = {{\tilde \mu }_0}{\boldsymbol{q}_0} + {\mu _0}{\boldsymbol{q}_1}
$
|
(31) |
|
$
\begin{array}{l}
{{\tilde \lambda }_1}{\boldsymbol{p}_0} + {\lambda _1}{\boldsymbol{r}_0} + 3\left( {{{\tilde \lambda }_0}{\boldsymbol{p}_1} + {\lambda _0}{\boldsymbol{r}_1}} \right) = \\
\;\;\;\;\;\;{{\tilde \mu }_1}{\boldsymbol{q}_0} + {\mu _1}{\boldsymbol{q}_1} + 3\left( {{{\tilde \mu }_0}{\boldsymbol{q}_1} + {\mu _0}{\boldsymbol{q}_2}} \right)
\end{array}
$
|
(32) |
|
$
\begin{array}{l}
{{\tilde \lambda }_1}{\boldsymbol{p}_1} + {\lambda _1}{\boldsymbol{r}_1} + {{\tilde \lambda }_0}{\boldsymbol{p}_2} + {\lambda _0}{\boldsymbol{r}_2} = \\
\;\;\;\;\;{{\tilde \mu }_1}{\boldsymbol{q}_1} + {\mu _1}{\boldsymbol{q}_2} + {{\tilde \mu }_0}{\boldsymbol{q}_2} + {\mu _0}{\boldsymbol{q}_3}
\end{array}
$
|
(33) |
|
$
\begin{array}{l}
3\left( {{{\tilde \lambda }_1}{\boldsymbol{p}_2} + {\lambda _1}{\boldsymbol{r}_2}} \right) + {{\tilde \lambda }_0}{\boldsymbol{p}_3} + {\lambda _0}{\boldsymbol{r}_3} = \\
\;\;\;\;\;3\left( {{{\tilde \mu }_1}{\boldsymbol{q}_2} + {\mu _1}{q_3}} \right) + \left( {{{\tilde \mu }_0}{\boldsymbol{q}_3} + {\mu _0}{\boldsymbol{q}_4}} \right)
\end{array}
$
|
(34) |
|
$
{{\tilde \lambda }_1}{\boldsymbol{p}_3} + {\lambda _1}{\boldsymbol{r}_3} = {{\tilde \mu }_1}{\boldsymbol{q}_3} + {\mu _1}{\boldsymbol{q}_4}
$
|
(35) |
根据式(31)~式(35)可得:
|
$
\left\{ \begin{array}{l}
{\lambda _0} = \frac{{\left( {{\mathit{\boldsymbol{p}}_0} - {\mathit{\boldsymbol{q}}_0}} \right) \cdot {\mathit{\boldsymbol{J}}_1}}}{{\left( {{p_0} - {r_0}} \right) \cdot {\mathit{\boldsymbol{J}}_1}}}\\
{\mu _1} = \frac{{\left( {{\mathit{\boldsymbol{p}}_0} - {\mathit{\boldsymbol{q}}_0}} \right) \cdot {\mathit{\boldsymbol{J}}_2}}}{{\left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right) \cdot {\mathit{\boldsymbol{J}}_2}}}\\
{\lambda _1} = \frac{{\left( {{\mathit{\boldsymbol{p}}_3} - {\mathit{\boldsymbol{q}}_3}} \right) \cdot {\mathit{\boldsymbol{J}}_3}}}{{\left( {{\mathit{\boldsymbol{p}}_3} - {\mathit{\boldsymbol{r}}_3}} \right) \cdot {\mathit{\boldsymbol{J}}_3}}}\\
{\mu _1} = \frac{{\left( {{\mathit{\boldsymbol{p}}_3} - {\mathit{\boldsymbol{q}}_3}} \right) \cdot {\mathit{\boldsymbol{J}}_4}}}{{\left( {{\mathit{\boldsymbol{q}}_4} - {\mathit{\boldsymbol{q}}_3}} \right) \cdot {\mathit{\boldsymbol{J}}_4}}}
\end{array} \right.
$
|
(36) |
其中J1=N1×(q1-q0), J2=N1×(p0-r0), J3=N2×(q4-q3), J4=N2×(p3-r3)。
而根据式(6)方向导数可推到出在点q0处:
|
$
\begin{array}{c}
{M_1} = \frac{{{\partial ^2}x}}{{\partial u\partial v}}{\mathit{\boldsymbol{n}}_{{q_0}}} = 4 \times 3 \times ({\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{p}}_1} - {\mathit{\boldsymbol{p}}_0}) \cdot {\mathit{\boldsymbol{n}}_{{q_0}}} = \\
12{n_{{q_0}}}({\mathit{\boldsymbol{p}}_1} - {\mathit{\boldsymbol{p}}_0})
\end{array}
$
|
(37) |
其余点运用同样方法可得方程(37)。根据点q0与q4处相邻曲面的法曲率需要与2.2.1节所计算的法曲率一致,从而可以构建法曲率一致的约束方程(38):
|
$
\left\{ \begin{array}{l}
12{\mathit{\boldsymbol{n}}_{{q_0}}} \cdot \left( {{\mathit{\boldsymbol{p}}_1} - {\mathit{\boldsymbol{p}}_0}} \right) = \\
\;\;\;\;\;\;\;\frac{1}{2}\left[ {{k_{{q_0}}}\left( {{E_1} + 2{F_1} + {G_1}} \right) - {L_1} - {N_1}} \right] = {M_1}\\
12{\mathit{\boldsymbol{n}}_{{q_0}}} \cdot \left( {{\mathit{\boldsymbol{r}}_1} - {\mathit{\boldsymbol{r}}_0}} \right) = \\
\;\;\;\;\;\;\;\frac{1}{2}\left[ {{{\tilde k}_{{q_0}}}\left( {{{\tilde E}_1} + 2{{\tilde F}_1} + {{\tilde G}_1}} \right) - {{\tilde L}_1} - {{\tilde N}_1}} \right] = {{\tilde M}_1}\\
12{\mathit{\boldsymbol{n}}_{{q_4}}} \cdot \left( {{\mathit{\boldsymbol{p}}_3} - {\mathit{\boldsymbol{p}}_2}} \right) = \\
\;\;\;\;\;\;\;\frac{1}{2}\left[ {{k_{{q_4}}}\left( {{E_2} + 2{F_2} + {G_2}} \right) - {L_2} - {N_2}} \right] = {M_4}\\
12{\mathit{\boldsymbol{n}}_{{q_4}}} \cdot \left( {{\mathit{\boldsymbol{r}}_3} - {\mathit{\boldsymbol{r}}_2}} \right) = \\
\;\;\;\;\;\;\;\frac{1}{2}\left[ {{{\tilde k}_{{q_4}}}\left( {{{\tilde E}_2} + 2{{\tilde F}_2} + {{\tilde G}_2}} \right) - {{\tilde L}_2} - {{\tilde N}_2}} \right] = {{\tilde M}_4}
\end{array} \right.
$
|
(38) |
将法曲率的约束条件(38)与连续的约束条件(27)联立:将式(27)代入式(38)可求出p1值,再将p1的值代入式(37)和(38)可求出r1、r2与p2,从而可以进一步求解出相应的内部控制点。图 5中的q0、q1、q2、q3、q4与图 1中P0, 0, 4、P0, 1, 3、P0, 2, 2、P0, 3, 1、P0, 4, 0相对应;而r1、r2则对应为待求解的内部控制点G0, 1, G0, 2。图 1中的另两条边界以及相对应的控制点Gi, j(G1, 1,G1, 2,G2, 1, G2, 2)可以类似求出。至此,对于给定的三角面Ti中的所有控制点均已经求出,从而确定了插值的四次Gregory曲面。
4 实验结果
通过C++进行编程,OpenGL进行显示,测试电脑配置为Intel i5-2430M 2.4 GHz,4 GB内存,测试了3个实例。
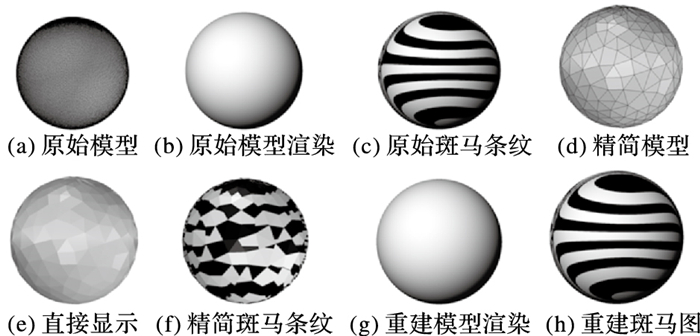
案例1为一单位球,原始模型为精细模型(如图 6(a)),对应的阴影渲染模型如图 6(b),斑马条纹模型如图 6(c),精简后的结果如图 6(d)。如果直接进行显示,效果如图 6(e),可见其非常不光顺,这一结果亦可从图 6(f)断裂的斑马条纹印证,说明该模型非G1连续。而经本文方法重建后的模型具有与原始模型同质量的渲染效果和斑马条纹效果,效果如图 6(g)和6(h),而网格数目如表 1已经大幅减少。观察该条纹不但连续而且光顺连接,这说明无跳跃点,也就是说明曲面拼接处顶点的法曲率变化接近相等。
表 1
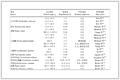
表 1 统计数据
| 图例 |
原始网格数 |
优化后网格数 |
运行时间/s |
| 图 6 |
65218 |
63 |
7.31 |
| 图 7 |
55681 |
1076 |
6.22 |
| 图 8 |
377895 |
8860 |
40.92 |
|
表 1 统计数据
|
案例2是复杂的维纳斯雕像模型,初始三角片规模为50000个,其对应的线框模型、阴影模型以及斑马条纹为图 7(a)~(c);简化后的网格模型的线框模型、阴影模型以及斑马条纹为图 7(d)~(f); 经过本算法插值后的效果则如图 7(g)与图 7(h)。对比图 7(h)与图 7(f),本文法线构建后的斑马模型是连续并且光顺的,接近原始模型的斑马条纹,但网格数目只有原始的2%左右。
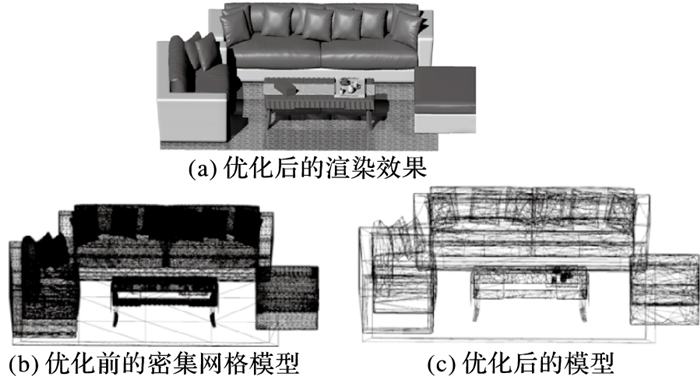
案例3来自互联网家具设计。对于互联网家具设计,网格数目过多会导致模型网络传输时间过长以及计算机处理效率低下。针对原始模型如图 8(b),该模型网格数目为37万以上,而整个场景的网格数目将会超过千万。通过该技术可大幅压缩网格数目后再进行传输从而极大节省带宽;接收后会在接收端通过所提算法进行快速图形重建, 从而以极低的存储和计算资源达到原始高质量的渲染效果如图 8(a)。
5 结语
本文推导获得了拼接顶点法曲率一致的约束条件,然后结合G1连续的约束条件,利用四次三角域Gregory曲面片插值G0连续的稀疏网格模型获得光顺的参数化模型。所获取的模型不但保证拼接处的G1连续,并解决了现有研究无法保证拼接顶点处法曲率一致的构建难题。实验表明该方法有效,对于稀疏模型的精细重构具有重要意义。