XIANG Ting, born in 1991, M. S. candidate. Her research interests include intelligent computing, numerical calculation
PAN Dazhi, born in 1974, Ph. D., professor. His research interests include intelligent computing, algorithm design
需求可拆分的车辆路径问题(Split Delivery Vehicle Routing Problem, SDVRP)最早由Dror等[1-2]在1989年提出,目前己经成为车辆路径问题(Vehicle Routing Problem, VRP)中一个较新的分支。与有容量限制的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP)只有1个约束条件的差异--允许顾客被多次访问。比如,实际的物流运作中,有的客户所要求的货物较多,超出了车辆承载能力, 这时必须对客户的需求进行拆分。Archetti等在文献[3-5]中证明了尽管SDVRP具有NP难(NP-hard)属性,但是对客户进行分割运输, 无论是总运输距离, 还是派车数目都比VRP更优化,而求解SDVRP的算法需要解决的关键问题是如何对需求进行合理优化的拆分。
自SDVRP提出后,国外学者提出了相应的启发式算法:Dror等[1]提出了解决SDVRP的局部搜索算法;Archetti等[6]首先设计了求解SDVRP的简单邻域搜索禁忌算法;Gendreau等[7]给出一种带广义插入的禁忌搜索算法实现SDVRP的求解;Archetti等[8]在禁忌搜索求解的基础上提出进一步优化算法。而国内研究主要着重于近似算法的设计上, 隋露斯等[9]设计了适合求解SDVRP的蚁群算法;孟凡超等[10]设计了特殊邻域搜索的禁忌搜索算法求解SDVRP;谢毅[11]设计了禁忌搜索算法和遗传算法,并将两种算法求解结果进行对比,发现遗传算法求解整体质量和速度不如禁忌搜索算法。近年来,在求解SDVRP时,通常将SDVRP分为两个子问题:分组和路径。根据解决子问题的先后顺序,又分为先分组后路径和先路径后分组两类方法。刘旺盛等在文献[12]中分别设计了先分组后路径及先路径后分组求解算法,并指出先分组后路径求得的解好于先路径后分组求得的解。文献[13]中设计了一种符合解特征的聚类方式(先分组后求解)求解该问题,并得到了不错的结果。熊浩等[14]提出了一种先求解再分组的算法--基于双层规划模型的三阶段禁忌算法,在大的旅行商问题(Traveling Saleman Problem,TSP)路径中切割增加路径。
本文结合需求可拆分车辆路径问题的解的特征,优先考虑大于等于车辆限载的客户,再结合客户间的距离和载重进行聚类分组,每组由一辆车配送,组内的线路优化是一个TSP。组内TSP的客户规模小,对算法的要求不高,本文采用基本蚁群算法求解。
1 SDVRP的数学模型本文研究的是单车场、单车型、无时间窗要求、纯装货(或纯卸货)的需求可拆分的车辆路径问题, 采用目前通用SDVRP的模型。具体问题描述为:n个客户点与车场中心集合C0={0}构成集合C={0, 1, 2,…, n}; 第i个客户对应的需求量为qi(i=1, 2, …, n);dij为集合{0, 1, 2,…, n}中任意2点i, j之间的距离;w为车辆的最大限载;R为完成任务所需的车辆数, 取值为:
| $R = \left[{\sum\limits_{i = 1}^n {\frac{{{q_i}}}{w}} } \right]$ | (1) |
变量xijr(r=1, 2, …, R; i, j=0, 1, …, n且i≠j)为:
| $x_{ij}^x = \left\{ \begin{array}{l} 1, \;\;\;第r辆车通过弧\left( {i, j} \right)\\ 0, \;\;\;其他 \end{array} \right.$ |
yir(r=1, 2, …, R, i=1, 2, …, n)为第r条线路中满足客户i的需求量;Sr代表第r条路线中服务的客户集合;Sr代表集合S所包含的元素个数。
模型适用范围为:1) 任意客户i, j的距离具有对称性,即dij=dji;2) 客户间的距离符合三角形不等式,即dik+dkj>dij;3) 所有车辆从车场出发,完成任务后返回车场;4) 每个客户的需求都要全部被安排,可以由1辆及多辆车满足。
以行车成本尽可能地低为目标,建立安排车辆分配数学模型如下:
| $\min \sum\limits_{r = 1}^R {\sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {{d_{ij}}x_{ij}^r} } } $ | (2) |
| $\begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}}\\ \;\;\;\;\sum\limits_{i = 0}^n {x_{ik}^r} = \sum\limits_{j = 0}^n {x_{kj}^r;} k = 0, 1, \cdots, n, r = 1, 2, \cdots, R \end{array}$ | (3) |
| $\sum\limits_{r = 1}^R {\sum\limits_{i = 0}^n {x_{ij}^r} } ;k = 0, 1, \cdots, n$ | (4) |
| $\sum\limits_{r = 1}^R {y_i^r = {q_i};i = 1, 2, \cdots, n} $ | (5) |
| $\sum\limits_{i \in {S^r}} {\sum\limits_{j \in {S^r}} {x_{ij}^r = \left| {{S^r}} \right|-1;r = 1, 2, \cdots R, {S^r} \subseteq C-{C_0}} } $ | (6) |
| $\sum\limits_{i = 1}^n {y_i^r \le w;r = 1, 2, \cdots, } R$ | (7) |
| $\sum\limits_{j = 0}^n {x_{ij}^r{q_i} \ge {y_{ri}};r = 1, 2, \cdots, R, i = 1, 2, \cdots, n} $ | (8) |
| $x_{ij}^r \in \left\{ {0, 1} \right\};i, j = 1, 2, \cdots, n, r = 1, 2, \cdots, R$ | (9) |
| ${q_i} \ge r_i^r \ge 0;i = 1, 2, \cdots, n, r = 1, 2, \cdots, R$ | (10) |
约束(3)表示进入某点的车辆数与离开该点的车辆数相等;约束(4)和(5)确保每个点至少被访问一次且需求均得到满足;约束(6)表示每条线路中被服务客户之间的弧边数等于被服务客户点的个数减1;约束(7)为车辆运载能力限制。
Dror等在文献[1-2]中分析需求可拆分问题的解的特征得出, 一个SDVRP可行解满足:1) 任意两条路线中最多只会存在一个共同点;2) 优化解中不会存在k-split cycle;3) 被拆分需求点的数量小于路线的数量。基于该问题的模型及可行解的特点,本文提出一种聚类算法对需求可拆分车辆路径问题进行求解。
2 求解SDVRP的聚类算法本文的聚类算法属于先分组后路径类型:第一阶段将客户聚类成R组,确定由同一辆车服务的客户集合;第二阶段是将每一组客户和车场构成一个TSP回路,利用蚁群算法求解每组的路径安排情况。
车辆路径问题中对客户聚类的主要目的是让相距较近的客户聚成一类,将原问题化为规模较小的TSP,降低问题的求解复杂度。而SDVRP中,存在着车辆载重和客户拆分的约束,故比单纯的无约束K均值算法(K-means Algorithm)更加复杂。本文设定一个拆分阈值,随机选择初始的聚类中心,采用距离优先准则选择待加入个体,满足拆分条件时进行拆分,过程主要分聚类方式和拆分策略两部分。
2.1 聚类方式定义1 设定一个拆分阈值参数cs(其中0 < cs < 1),取值由平均载重和车辆限载的比值(简称:平均载重率)
| 表 8 各实验中平均载重率和cs的取值 |
聚类步骤如下:
步骤1 由式(1)计算完成任务所需的车辆数R, 确定cs的取值。
步骤2 载重满足qi=w的客户i优先安排到一辆车中。超过w的个体拆分为w和qi-w两部分,载重qi-w的部分作为一个新的个体加入未安排的客户群体。若这两类客户共有p个,则只剩下R-p辆车未安排,取初始r=1。
步骤3 未安排的客户中随机地选择一个个体j作为聚类中心。
步骤4 计算未安排的客户g1, g2, …, gn到该聚类中心的距离dOgj,最小的距离为dOgk=min(dOgj)(j=1, 2, …, n),对应的未安排客户为gk。
步骤5 判断客户gk是否加入该车辆:1) 若该车辆已有载重Qs满足:Qs+qgk≤w,将客户gk放入车辆中并返回步骤4;2) 若Qs+qgk>w且Qs≥cs·w,结束该车辆的安排并进入步骤6; 3) 若Qs+qgk>w且Qs < cs·w, 该车辆已安排的客户和客户gk进入拆分策略(具体方式见2.2节),然后结束该车辆安排并进入步骤6。
步骤6 若r < R-p,更新r=r+1, 并返回步骤3安排下一辆车,否则结束聚类。
该聚类方式中,分阈值参数cs的选取,使得最终得到的分组中每辆车的载重都在[cs·w, w]内。cs取值太小,容易导致最终部分客户得不到安排,出现不可行解;cs太大,会导致拆分个体偏多和最后一辆车载重低,出现车辆载重分布不均衡现象;一般cs取值在区间
在2.1节中遇到需要拆分客户时,综合考虑拆分的客户数更少、车辆尽量满载且路径较短等要求,本文设计了一种拆分策略:拆分点在gk和当前车辆已安排的客户p1, p2, …, pk中选择;拆分标准由聚类中心到gk和各客户pi的距离之差Δdi来确定。
定义2 Δdi=dOpi-dOgk,其中:dOpi为聚类中心O到客户pi的距离,dOgk为聚类中心O到客户gk的距离,聚类中心O的坐标为
拆分的具体策略为:
1) 若存在客户pj,对应的载重量qpj和车辆的剩余载重Qw满足:Qw+qpl=qgk,则将客户pj剔出车辆,同时将客户gk加入。
2) 若max(Δdi)≤0,则直接将客户gk拆分为载重为Qw和qgk-Qw两部分,载重为Qw的部分加入车辆中,另一部分作为一个新个体加入未安排的客户群体内。
3) 若存在部分个体ps1, ps2, …, pst对应的Δdst>0,则在这部分个体中:
①若存在客户psj满足:qpsj+Qw < qgk,车辆中剔出Δd最大的个体psj,加入并拆分客户gk载重为qpsj+Qw和qgk-qpsj-Qw两部分。载重为qpsj+Qw的部分加入车辆中使得满载,另一部分作为一个新个体加入未安排的客户群体内。
②若所有客户ps1, ps2, …, pst对应的载重有:qpsj>qgk(j=1, 2…, t),直接将客户gk加入车辆,同时将max{Δdi}对应的客户psj拆为载重为qgk-Qw和qpsj+Qw-qgk两部分。载重为qgk-Qw的部分保留在当前车辆中,另一部分作为一个新个体加入未安排的客户群体内。
③否则将客户ps1, ps2, …, pst中min{ qp sj + Qw-qgk }对应的客户psj变为未安排的客户,同时让车辆为客户gk服务。
2.3 算法的求解步骤本文算法是先聚类确定同一辆车服务的客户点,然后再确定最终的路线,可以说聚类的好坏直接影响着最终路线的好坏。然而需求可拆分的车辆路径问题是带约束条件的聚类, 计算不一定收敛。本文采用文献[13]的方式,设置一个迭代参数T, 聚类T次选择最好的一种方式作为最优的聚类结果。聚类评估函数由式(11)决定:
| $\min (sum(D)) = \sum\limits_{j = 1}^R {\sum\limits_{i \in {C_j}} {{d_{ij}}} } $ | (11) |
其中Cj代表聚类j,即计算聚类中的每个客户到该类中心的距离之和,选取距离之和最小的作为最优聚类结果。2.1节的聚类方式可能出现聚类结束之后部分个体未安排或是没安排完,这样的聚类结果称为不可行分组,设定其聚类评估函数值为无穷大。算法的步骤如下:
步骤1 设定一个迭代参数T, 迭代次数t=0。
步骤2 由式(1)计算所需车辆数目R,按照2.1节的方式对客户进行聚类,当需要进入2.2节的拆分策略前,先更新该车辆中已安排客户的聚类中心(x, y)坐标为:
| $\left\{ \begin{array}{l} x = \frac{1}{k}\sum\limits_{l = 1}^k {{x_{{p_l}}}} \\ y = \frac{1}{k}\sum\limits_{l = 1}^k {{y_{{p_l}}}} \end{array} \right.$ |
其中(xpl, ypl)为该车辆中客户pl的坐标。
步骤3 若所有的车辆都已被安排,结束当前代聚类;
步骤4 更新t=t+1并判断是否t≤T:若是,则返回步骤2进行下一次聚类;否则结束整个聚类过程,进入步骤5。
步骤5 按照式(11)的评估函数找到T次迭代中最好的聚类方式。
步骤6 采用蚁群算法对步骤5得到的聚类结果中各类进行TSP线路优化。
3 实验结果及分析为测试算法的有效性,本文采用以往文献中的数据进行测试,并主要与现有的聚类算法[13]进行比较。算法由Matlab 7.0编程实现,在CPU为3.3 GHz,内存为8 GB的Windows 7操作系统的计算机上面运行。
3.1 实验1文献[13]设计的聚类算法求解了一个包含15个客户点、车辆的最大运载量为500的SDVRP。本文采用该例对新提出的聚类方式进行测试,拆分阈值参数cs=0.9,取聚类迭代次数T=500, 运行10次的结果与文献[13]进行对比,结果见表 1。
| 表 1 实验1的结果对比 |
本文提出的聚类算法在10次测试中得到的最优路径长度为1721.7,比文献[13]的1764.5缩短了2.4%,平均解的质量有所提高,解的稳定性更好,本文算法相比文献[13]的搜索能力和鲁棒性都有所提高。表 2中给出了本文最优解的线路安排,该方案中需要拆分的顾客点为:1, 5, 7, 9, 14。
| 表 2 实验1对应的最优线路 |
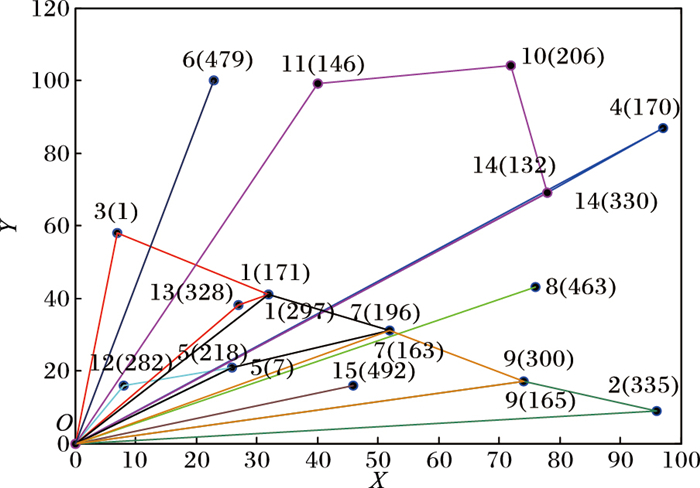
图 1为本文中算法求解的实验1的最优线路安排,图中黑色圆点表示顾客,O表示车场中心,圆点旁的数字表示客户序号,括号中的数字表示运输量, 客户1、5、7、9、4由2辆车服务,对应2条线路,每条线路对应一组运输量。如客户14,会出现路线5中的14(330)和路线7中的14(132)。
|
图 1 实验1的最优线路安排 |
文献[13]的聚类算法还求解了20个客户的SDVRP, 本文也采用该实例进行实验。由于客户的总载重量为40,8辆车的装载量也为40,设定拆分阈值参数cs=0.92。聚类迭代次数T=500, 运行10次,将实验结果进行对比,具体见表 3。
| 表 3 实验2的结果对比 |
本文算法得到的最优路径比文献[13]算法得到的最优路径缩短约3.8%,且解更加稳定,运算时间上也有明显降低。表 4给出了本文算法最优路径的安排,该安排中需要拆分的客户为18。
| 表 4 实验2对应的最优线路 |
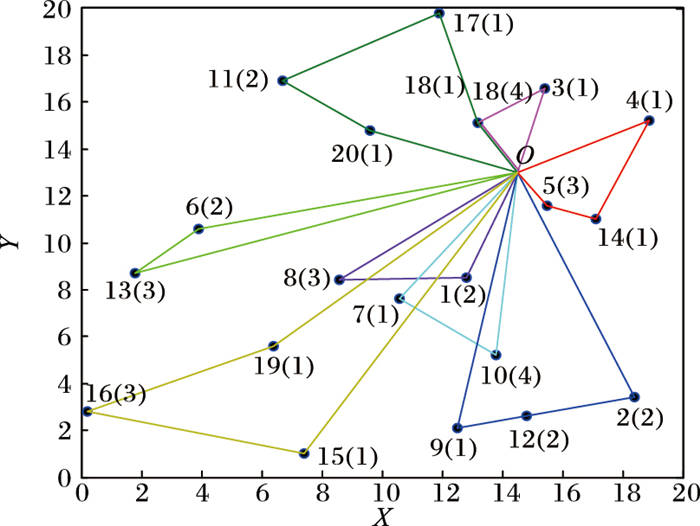
图 2为本文中算法求解的最优线路安排,图中黑色圆点表示顾客,O表车场中心,圆点旁的数字表示客户序号,括号中的数字表示运输量,客户18由线路1和线路3共同完成,对应的载重量分别为4和1,故会出现18(4)和18(1)。
|
图 2 实验2的最优线路安排 |
文献[10]给出了36个点的配送问题,车辆容量为1,其中有两个顾客点17和10的需求量超过车辆装载量。本文算法和文献算法均对其进行求解,本文算法中设定聚类迭代次数T=500,cs=0.93,运行10次,得到最优解路径长度336.74,相对文献[13]得到的结果354.7缩短了5.1%,表明本文算法在解决中等规模的需求可拆分车辆路径问题中也具有较好的搜索能力。表 5给出了与文献[13]的结果对比,表 6为对应的最优线路安排。
| 表 5 实验3的结果对比 |
| 表 6 实验3对应的最优线路 |
文献[6]和文献[13]分别设计了禁忌搜素算法和聚类算法求解来自文献[6]的7组benchmark数据,实验证明文献[13]的结果明显优于文献[6]。本文选择其中客户点数为50的例子P01与文献[13]进行对比,该组的后缀“00”表示原问题,其他后缀为按照文献[6]的方式变异客户的需求量,如后缀为“1030”表示:客户需求量均介于车辆运载量的10%~30%。设定聚类迭代次数T=1000,各运行10次。对应的cs取值、路径长度和运算时间见表 7。
| 表 7 实验4的结果对比 |
实验结果表明:随着问题规模的增大,本文算法相比文献[13]的求解最优解能力和运算效率优势越明显。
实验1~4表明:针对中小型规模的需求可拆分车辆路径问题,本文算法无论是在搜索能力、运算时间,还是解的鲁棒性方面都明显地优于文献[13]算法。
3.5 参数cs的取值分析从上文分析中可知:拆分阈值参数cs将每辆车的载重都限定在[cs·w, w]内。cs取值太小,容易导致最终部分客户得不到安排,出现不可行解;cs太大,会导致拆分个体偏多和最后一辆车载重低,出现车辆载重分布不均衡现象;cs的大致范围可以由平均载重率决定。表 8给出了本文中的各个实验中平均载重率的取值、对应的cs以及两者之差sd。
由表 8可知:本文中的各实例平均载重率均在95%~100%,对应的cs取值在0.9~0.95,差值sd的范围为:0.0295~0.08;以0.01为1个单位,将cs的取值范围限定在区间
聚类算法求解需求可拆分车辆路径问题的关键在于客户点的拆分和分组,而实际生活中也应充分考虑车辆载重的均衡性。本文算法引入拆分阈值,将车辆载重限定在一个确定区间内; 客户分组时采用就近原则; 当车辆原载重未达到载重范围最小值而加入客户后超出限载时,对客户进行拆分和调整; 客户的拆分策略充分考虑待拆分客户点载重、车辆剩余载重以及各客户点到当前组各中心的距离关系;实例对本文算法进行测试,并与文献[13]的结果对比表明,本文算法针对中小型SDVRP具有运算快、鲁棒性高、搜索能力强的特点。随着问题规模的增大,SDVRP的搜索难度会呈指数倍增长,如何进一步提高算法的搜索能力是下一步研究的重点。
| [1] | DROR M, TRUDEAU P. Split delivery routing[J]. Naval Research Logistics, 1990, 37 (3) : 383-402. doi: 10.1002/nav.v37.3 |
| [2] | DROR M, TRUDEAU P. Savings by split delivery routing[J]. Transportation Science, 1989, 23 (2) : 141-145. doi: 10.1287/trsc.23.2.141 |
| [3] | ARCHETTIC C, FEILLET D, GENDREAU M, et al. Complexity of the VRP and SDVRP[J]. Transportation Research Part C:Emerging Technologies, 2011, 19 (5) : 741-750. doi: 10.1016/j.trc.2009.12.006 |
| [4] | ARCHETTIC C, MANSINI R, SPERANZA M G. Complexity and reducibility of the skip delivery problem[J]. Transportation Science, 2005, 39 (2) : 182-187. doi: 10.1287/trsc.1030.0084 |
| [5] | ARCHETTIC C, SAVELSBERGH M W, SPERANZA M G. Worst-case analysis for split delivery vehicle routing problems[J]. Transportation Science, 2006, 40 (2) : 226-234. doi: 10.1287/trsc.1050.0117 |
| [6] | ARCHETTIC C, SPERANZA M G, HERTZ A. A tabu search algorithm for the split delivery vehicle routing problem[J]. Transportation Science, 2006, 40 (1) : 64-73. doi: 10.1287/trsc.1040.0103 |
| [7] | GENDREAU M, HERTZA A, LAPORTE G. A tabu search heuristic for the vehicle routing problem[J]. Management Science, 1994, 40 (10) : 1276-1290. doi: 10.1287/mnsc.40.10.1276 |
| [8] | ARCHETTIC C, SAVELSBERGH M W, SPERANZA M G. An optimization-based heuristic for the split delivery vehicle routing problem[J]. Transportation Science, 2008, 42 (1) : 22-31. doi: 10.1287/trsc.1070.0204 |
| [9] | 隋露斯, 唐加福, 潘震东, 等.用蚁群算法求解需求可拆分车辆路径问题[C]//2008年中国控制与决策会议论文集.沈阳:东北大学出版社, 2008:997-1001. ( SUI L S, TANG J F, PAN Z D, et al. Ant colony algorithm to solve split delivery vehicle routing problem[C]//Chinese Control and Decision Conference 2008. Shenyang:Northeastern University Press, 2008:997-1001. ) |
| [10] | 孟凡超, 陆志强, 孙小明. 需求可拆分车辆路径问题的禁忌搜索算法[J]. 计算机辅助工程, 2011, 19 (1) : 78-83. ( MENG F C, LU Z Q, SUN X M. Taboo seach algorithm of split delivery vehicle routing problem[J]. Computer Aided Engineering, 2011, 19 (1) : 78-83. ) |
| [11] | 谢毅.需求可拆分的物流车辆路线问题研究[D].上海:同济大学, 2006. ( XIE Y. Research on split delivery vehicle routing problem[D].Shanghai:Tongji University, 2006. ) |
| [12] | 刘旺盛, 黄娟. 需求可拆分的车辆路径问题的分段求解[J]. 集美大学学报(自然科学版), 2011, 16 (1) : 38-44. ( LIU W S, HUANG J. Two-stage algorithm for split delivery vehicle routing problem[J]. Journal of Jimei University (Natural Science), 2011, 16 (1) : 38-44. doi: 10.1007/s11859-011-0708-0 ) |
| [13] | 刘旺盛, 杨帆, 李茂青, 等. 需求可拆分车辆路径问题的聚类求解算法[J]. 控制与决策, 2012, 27 (4) : 535-541. ( LIU W S, YANG F, LI M Q, et al. Clustering algorithm for split delivery vehicle routing problem[J]. Control and Decision, 2012, 27 (4) : 535-541. ) |
| [14] | 熊浩, 鄢慧丽. 需求可拆分车辆路径问题的三阶段禁忌算法[J]. 系统工程理论与实践, 2015, 35 (5) : 1230-1235. ( XIONG H, YAN H L. A three-phase tabu seach heuristic for the split delivery vehicle routing problem[J]. Systems Engineering-Theory & Practice, 2015, 35 (5) : 1230-1235. ) |




