2. 大数据统计分析与优化控制河南省工程实验室(河南师范大学), 河南 新乡 453007
2. Henan Engineering Laboratory for Big Data Statistical Analysis and Optimal Control(Henan Normal University), Xinxiang Henan 453007, China
QIU Yana, born in 1990, M. S. candidate. Her research interests include combinatorial network optimization.
YANG Yuxing, born in 1981, Ph. D., associate professor. His research interests include graph and combinatorial network optimization.
目前,大数据的处理和复杂问题的解决对并行计算机的计算能力已近乎苛刻。为了大幅提高计算能力,并行计算机系统的处理器数目急剧增加,从而导致处理器之间的通信开销越来越大。在超级并行计算机系统中,处理器之间的连接模式(即底层网络)对整个系统的硬件消耗、通信性能等方面起着重要的、甚至是决定性的作用。
在实际的系统中,元器件和直连线路难免发生故障。在故障发生时,人们自然希望该系统的任意两个节点之间依旧可以通信; 反映在其底层网络中,人们希望网络依旧连通。连通度和边连通度是度量网络连通性和容错能力的主要参数。然而,这两个参数存在一个明显的缺陷,它认为“和同一个节点相关联的所有边”或“和一条边相关联的所有节点”很有可能同时发生故障。然而,在实际的系统中,同时故障几乎是不可能的。为弥补这一不足,Esfahanian等[1]对发生故障的系统的各个分支加以限制,提出了条件连通度和条件边连通度的概念。自此,许多经典网络的条件连通度[2-4]和条件边连通度被相继研究[5-6], 其中,泡型网络(bubble-sort network)是并行计算机系统的主要候选网络之一,它具有正则性、点对称性、二部性、层次性等优秀的拓扑性质[7-10]。
n维泡型网络的边连通度仅为n-1,限制边连通度仅为2n-4,从而导致其容错能力不强。为此,在泡型网络的基础上设计了一种保留了泡型网络的大多数优秀拓扑性质的增广泡型网络, 并证明了n≥3时,n维增广泡型网络的边连通度为n,限制边连通度为2n-2。对比结果表明,增广泡型网络比泡型网络具有更高的连通性和更强的容错能力。
1 泡型网络与增广泡型网络对于正整数n,记Nn={1, 2, …, n}。图G中节点v的度记为dG(v),最小节点度记为Δ(G),边连通度记为λ(G),限制边连通度记为λ′(G)。未加定义而直接使用的图论术语与符号参见文献[10]。
n维泡型网络Bn是一个拥有n!个节点和(n-1)n!/2条边的无向图。在Bn中,每个节点的标号形如δ1δ2…δn,其中,δi∈Nn(i∈Nn)且对于j∈Nn,若j≠i,则δi≠δj。两个节点x=x1x2…xn和y=y1y2…yn相邻,当且仅当存在一个整数i∈Nn-1,使得xi=yi+1,yi=xi+1且对于任意的整数j∈Nn\{i, i+1},有xj=yj。此时,连接x和y的边叫作Bn的一条i维边。
不难看出,Bn是n-1正则的,即Bn中每个节点的度均为n-1。Bn具有层次结构,更为具体地讲,删除Bn的所有1维边(或n-1维边)可以将Bn划分为n个互不相交的、与Bn-1同构的子网。
定义1 n维增广泡型网络Rn是一个无重边和自环的无向图,其中,V(Rn)=V(Bn)。两个节点x=x1x2…xn和y=y1y2…yn相邻,当且仅当:
1)x和y在Bn中相邻;
2)x1=yn,y1=xn且对于任意的整数i∈Nn\{1, n},有xi=yi。
由1)得到的边叫Rn的Ⅰ类边;由2)得到的边叫Rn的Ⅱ类边。
由定义1可知,当n≤2时,Rn同构于Bn,此时它是n-1正则的。当n≥3时,Rn是n正则的。记Rn的Ⅱ类边组成的集合为M。由Rn的定义可知,Rn=Bn∪M且M是一个完美匹配。将Rn中的Bn沿第一维划分为n个互不相交的Bn-1,分别记为1Xn-1、2Xn-1、…、nXn-1。对于iXn-1中任意一个节点,其不在iXn-1中的邻点称作它的外邻点,一个节点和它的外邻点之间的边称作它的外邻边。易知,当n≥3时,Rn的每个节点u的外邻点个数outv(u)和外邻边的条数oute(u)均为2。
1~4维增广泡型网络的拓扑结构如图 1所示。
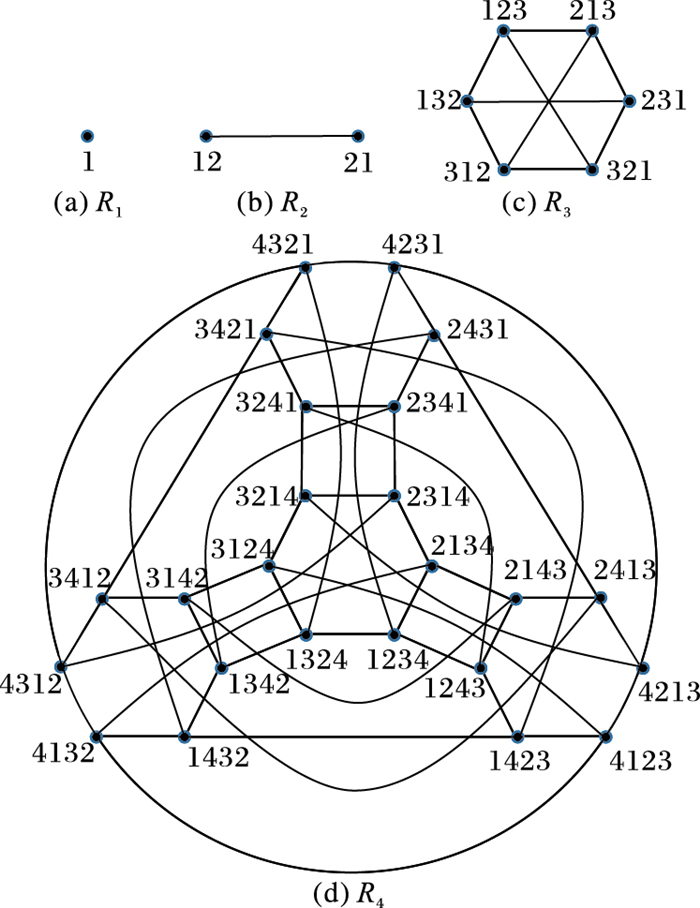
|
图 1 1~4维增广泡型网络 |
本章将研究Rn的边连通度和限制边连通度。首先介绍两个重要的引理。
引理1[11] λ(G)≤Δ(G)。
引理2[12] 当n≥2时,λ(Bn)=n-1;当n≥3时,λ′(Bn)=2n-4。
定理1 当n≥3时,Rn中的任意两个Bn-1之间有(n-2)!条Ⅰ类边和(n-2)!条Ⅱ类边。
证明 不妨设两个Bn-1为iXn-1和jXn-1。在iXn-1和jXn-1之间存在形如(ija1a2…an-2, jia1a2…an-2)的Ⅰ类边,和形如(ia1a2…an-2j, ja1a2…an-2i)的Ⅱ类边,其中,对于任意的k∈Nn-2,有ak∈Nn\{i, j}。所以,iXn-1和jXn-1之间的Ⅰ类边和Ⅱ类边均为(n-2)!条。证毕。
2.1 Rn的边连通度首先,R1是仅有一个节点的空图,它不存在边割。而R2与B2同构,λ(R2)=λ(B2)=1。接下来,研究当n≥3时,n维增广泡型网络Rn的边连通度。
定理2 当n≥3时,λ(Rn)=n。
证明 当n≥3时,Rn是n正则的。由引理1得,λ(Rn)≤Δ(Rn)=n。下面证明λ(Rn)≥n。
设F⊂E(Rn)(|F|≤n-1)为故障边集。接下来,只需证F不是Rn的边割,即Rn-F依然连通。当n=3时,容易验证,对于任意的|F|≤2,R3-F依然连通。现只需考虑n≥4情况。记F在iXn-1下的限制(即F∩E(iXn-1))为Fi,其中i∈Nn。分两种情况讨论。
情况1 对于任意的i∈Nn均有|Fi|≤n-3。因|Fi|≤n-3,由引理2知,每一个iXn-1都是连通的。由定理1可得,任意两个Bn-1之间有(n-2)!×2条边。而|F|≤n-1 < (n-2)!×2,所以任意两个Bn-1之间依然存在非故障边相连。进而可知,Rn-F连通。
情况2 存在i∈Nn使得|Fi|≥n-2。此时,必定只有一个i∈Nn使得|Fi|≥n-2,否则对于n≥4,将有|F|≥2|Fi|≥2(n-2)>n-1,与假设条件|F|≤n-1矛盾。不失一般性,设|F1|≥n-2。此时,由引理2知,对于任意的i∈Nn\{1},iXn-1均连通。类似于情况1的证明,易知,除1Xn-1之外的任意两个Bn-1之间均有非故障边相连。接下来,只需证1Xn-1的任意一个节点均与1Xn-1之外的某个Bn-1连通即可。因为|F|≤n-1且|F1|≥n-2,所以Rn-1Xn-1中至多有一条故障边。对于1Xn-1的任一节点v=1kx1x2…xn-3m,它有两个外邻点,即u=k1x2…xn-3m和w=mkx1x2…xn-21。而Ⅰ类边(u, v)和Ⅱ类边(w, v)中至多只有一条故障边,不妨设(u, v)为非故障边,则v通过边(u, v)和kXn-1连通。进而,Rn-F连通。
综上可得,当n≥3时,λ(Rn)=n。证毕。
定理2表明,对于n≥3时的n维增广泡型网络,当其中的故障边数不超过n-1时,该网络依然是连通的。
2.2 Rn的限制边连通度R1和R2均不存在限制边割。下面,研究当n≥3时,n维增广泡型网络Rn的限制边连通度。
定理3 当n≥3时,λ′(Rn)=2n-2。
证明 设u, v∈V(Rn)且(u, v)∈E(Rn)。令F为与u或v关联(但不同时与u和v都关联)的边组成的集合。则|F|=2n-2。显然,Rn-F不连通,且Rn-F没有孤立点,即F是Rn的一个限制边割,故λ′(Rn)≤|F|=2n-2。
接下来,只需证明λ′(Rn)≥2n-2。设F⊂E(Rn),|F|≤2n-3且Rn-F没有孤立点。证明Rn-F依然连通即可。当n=3时,易知,对于任意的|F|≤3,R3-F依然连通。下面考虑n≥4情况。令Fi=F∩E(iXn-1),其中i∈Nn。分3种情况讨论。
情况1 对于任意的i∈Nn均有|Fi|≤n-3。
因为|Fi| ≤n-3,由引理2知,每一个iXn-1都是连通的。由定理1可知,任意两个Bn-1(iXn-1和jXn-1)之间共有(n-2)!×2边。
当n≥5时,|F|≤2n-3 < (n-2)!×2,所以任意两个Bn-1之间依然存在非故障边相连。进而可知,Rn-F连通。
当n=4时,故障边至多有2n-3=5条。iXn-1和jXn-1之间有(n-2)!×2=4边。若这4条边不全为故障边,则iXn-1和jXn-1连通。若这4条边全是故障边,则除此之外至多还有1条故障边。此时,iXn-1、jXn-1与另一个Bn-1均由至少(n-2)!×2-1=3条非故障边连通;进而,有Rn-F连通。
情况2 恰好存在一个i∈Nn使得|Fi|≥n-2。
不失一般性,设|F1|≥n-2。在此情况下,对于任意的i∈Nn\{1},均有|Fi|≤n-3。由引理2知,iXn-1连通。除了1Xn-1之外的任意两个Bn-1之间有(n-2)!×2边。而|F|≤2n-3 < (n-2)!×2,所以任意两个Bn-1之间依然存在非故障边相连。
接下来只需证明对于1Xn-1的任意一个节点v均与1Xn-1之外的某个Bn-1连通即可。用反证法,设v均与除1Xn-1之外的任何Bn-1均不连通。
首先,v的两条外邻边都是故障的,否则v可以通过非故障的外邻边与1Xn-1之外的某个Bn-1连通。
因为Rn-F没有孤立点,所以,v在1Xn-1中至少存在一个邻点w使得(v, w)∉F。w的两条外邻边也必定都是故障的,否则v可以通过(v, w)及一条非故障的外邻边与1Xn-1之外的某个Bn-1连通。
因为v不与1Xn-1之外的任意一个Bn-1连通,所以对于v的任意邻点x,要么(v, x)为故障边,要么x的两条外邻边均为故障边。类似地,对于w的任意邻点y,要么(w, y)为故障边,要么y的两条外邻边均为故障边。设1Xn-1中与v关联的故障边的条数为ev,与w关联的故障边的条数为ew。则在1Xn-1中,除了边(w, v)之外与v关联的“非故障边”还有d1Xn-1(v)-ev=n-3-ev条。由于v不能与1Xn-1之外的某个Bn-1连通,故而与v关联的每条“非故障边”的另一个端点的两条外邻边都是故障边,这将产生2(n-3-ev)条故障边。类似地,除了边(w, v)之外与w关联的非故障边还有d1Xn-1(w)-ew=n-3-ew条。因为w不能与1Xn-1之外的某个Bn-1连通,所以与w关联的“非故障边”的其他端点的2(n-3-ew)条外邻边也均为故障边,而且这2(n-3-ew)条边与上述2(n-3-ev)条边两两不同(因为v和w没有公共邻点)。注意d1Xn-1(w)=d1Xn-1(v)=n-2,oute(v)=oute(v)=2,ew≤d1Xn-1(w)-1,ev≤d1Xn-1(v)-1。综上可得,故障边的条数至少为:
| $\begin{align} &oute(v)+oute(w)+{{e}_{w}}+{{e}_{v}}+2(n-3-{{e}_{v}})+\\ &2(n-3-{{e}_{w}})=2+2+4(n-3)-({{e}_{w}}+{{e}_{v}})=\\ &4n-8-({{e}_{w}}+{{e}_{v}})\le 4n-8- \\ &({{d}_{1{{X}^{n-1}}}}(w)-1+{{d}_{1{{X}^{n-1}}}}(v)-1)=\\ &4n-8-(n-2-1+n-2-1)=2n-2.\\ \end{align}$ |
这与前提条件“故障边条数|F|≤2n-3”矛盾。所以,v与1Xn-1之外的某个Bn-1连通。
情况3 恰好存在两个不同i, j∈Nn,使得|Fi|≥n-2,|Fj|≥n-2。
由对称性,不妨设|F1|≥n-2,|F2|≥n-2。在此情况下,对于任意的i∈Nn\{1, 2},均有|Fi|≤n-3。由引理2知,iXn-1连通。此时,在1Xn-1和2Xn-1之外至多还有|F|-|F1|-|F2|≤2n-3-2(n-2)=1条故障边。易知,除1Xn-1和2Xn-1之外的所有Bn-1均连通。接下来只需证明对于1Xn-1和2Xn-1的任意一个节点v均与1Xn-1及2Xn-1之外的某个Bn-1连通即可。不妨设v是1Xn-1中的点。显然,v至少有一条外邻边是“非故障”的。
若v的两条外邻边均为非故障边,由外邻边的定义及子网划分方式可知,这两条外邻边必然有一条连接到2Xn-1之外的某个Bn-1。
若v的两条外邻边恰有一条非故障边并且该边连接到2Xn-1之外的某个Bn-1,则结果成立。
若v的两条外邻边恰有一条非故障边并且该边连接到2Xn-1中的某一节点u,则u的除(u, v)的那条外邻边必然是“非故障边”,并且该边连接到1Xn-1之外的某个Bn-1。
综上,无论哪种情况,均有Rn-F连通。 证毕。
定理3表明,对于n≥3时的n维增广泡型网络,当其中的故障边数不超过2n-3且删除这些边后的残网中没有孤立点,则残网依然连通。
3 连通性及容错能力对比本章将从理论分析与实例推导两个方面分别对Bn和Rn的连通性与容错能力加以比较。
3.1 连通性比较分析由Rn和Bn的结构可知,R1和R2分别与B1和同构B2。当n≥3时,Rn和Bn的主要参数对比如表 1所示。
| 表 1 Rn与Bn的主要参数对比 |
在维数相同的情况下,Rn的边连通度比Bn的边连通度大1;Rn的限制边连通度比Bn的限制边连通度大2。由于在维数相同的情况下,Rn的节点度数比Bn大1,这就意味着搭建Rn比搭建Bn需要稍多的物理线路。因此,使用“边连通度与节点度数之比”和“限制边连通度与节点度数之比”能够更好地比较增加这些物理线路所带来的“性价比”。对于n维泡型网络来说,其边连通度与节点度数之比为λ(Bn)/d(Bn)=(n-1)/(n-1)=1,限制边连通度与节点度数之比为λ′(Bn)/d(Bn)=(2n-4)/n=2-4/n;对于n维增广泡型网络来说,其边连通度与节点度数之比为λ(Rn)/d(Rn)=n/n=1,限制边连通度与节点度数之比为λ′(Rn)/d(Rn)=(2n-2)/n=2-2/n。在“边连通度与节点度数之比”保持不变的情况下,增广泡型网络比泡型网络具有更高的“限制边连通度与节点度数之比”。
上述对比结果表明,与泡型网络相比,增广泡型网络具有更好的连通性。
3.2 容错能力比较实例一般来说,网络的边连通度和限制边连通度越大,其可靠性(容错能力)越强。网络的可靠性通常在Moore-Shannnon模型[1]下,依据网络的边连通度或限制边连通度而计算。网络G的边数为|E(G)|,假设节点不发生故障,边以相同的概率p发生故障。
在传统的边故障模型下,网络G的可靠性(容错能力)可用式(1)度量:
| $R(G, p)=1-\sum\limits_{i=\lambda(G)}^{|E(G)|}{{{m}_{G, i}}{{p}^{i}}{{(1-p)}^{|E(G)|-i}}}$ | (1) |
其中:λ(G)为G的边连通度,mG, i为G的阶数为i的“边割”的数目。
在不产生孤立节点的条件边故障模型下,用式(2)度量网络G的可靠性:
| $ R'(G, p)=1-\sum\limits_{i=\lambda '(G)}^{|E(G)|}{m{{'}_{G, i}}{{p}^{i}}{{(1-p)}^{|E(G)|-i}} } $ | (2) |
其中:λ′(G)为G的限制边连通度,m′G, i为G的阶数为i的“限制边割”的数目。
显然,若要计算网络的可靠性,需要计算其边割或限制边割的数目。然而,要确定网络中所有的边割或限制边割的数目已被证明是NP困难的。下面,以3维泡型网络B3和3维增广泡型网络R3为例计算并比较它们的可靠性。由定义可知,3维泡型网络B3是一个包含6个节点的圈,其边数|E(B3)|=6;3维增广泡型网络R3也有6个节点,边数|E(R3)|=9,其结构如图 1(c)所示。
例1 计算p=0.1时,在“传统边故障模型”泡型网络B3和增广泡型网络R3的可靠性。
解 在传统边故障模型下,分别由引理2和定理2可知λ(B3)=2、λ(R3)=3。易得:mB3, i=C6i,其中2≤i≤6;mR3, 3=6、mR3, 4=45、mR3, j=C9j,其中5≤j≤9;由式(1)可得B3的可靠性R(B3, p)和R3的可靠性R(R3, p)分别为:
| $ \begin{align} &R({{B}_{3}}, p)=R({{B}_{3}}, 0.1)=\\ &\ \ \ \ \ \ 1-\sum\limits_{i=\lambda({{B}_{3}})}^{|E({{B}_{3}})|}{{{m}_{{{B}_{3}}, i}}{{p}^{i}}{{(1-p)}^{|E({{B}_{3}})|-i}}=} \\ &1-\sum\limits_{i=2}^{6}{C_{6}^{i}\times {{0.1}^{i}}\times {{(1-0.1)}^{6-i}} } \approx 0.8857 \\ \end{align} $ |
| $ \begin{align} &R({{R}_{3}}, p)=R({{R}_{3}}, 0.1)=\\ &1-\sum\limits_{i=\lambda({{R}_{3}})}^{|E({{R}_{3}})|}{{{m}_{{{R}_{3}}, i}}{{p}^{i}}{{(1-p)}^{|E({{R}_{3}})|-i}}=} \\ &1-6\times {{0.1}^{3}}\times {{0.9}^{6}}-45\times {{0.1}^{4}}\times {{0.9}^{5}}- \\ &\sum\limits_{i=5}^{9}{C_{9}^{i}\times {{0.1}^{i}}\times {{(1-0.1)}^{9-i}} \approx 0.9933} \\ \end{align} $ |
例2 计算p=0.1时,在“条件边故障模型”泡型网络B3和增广泡型网络R3的可靠性。
解 在条件边故障模型下,分别由引理2和定理3可知λ′(B3)=2、λ′(R3)=4。易得:m′B3, 2=9、m′B3, 3=2、m′B3, 4=m′B3, 5=m′B3, 6=0;而m′R3, 4=9、m′R3, 5=42、m′R3, 6=6、m′R3, 7=m′R3, 8=m′R3, 9=0。由式(2)可得B3的可靠性R′(B3, p)和R3的可靠性R′(R3, p)分别为:
| $ \begin{align} &R'({{B}_{3}}, p)=R'({{B}_{3}}, 0.1)=\\ &1-\sum\limits_{i=\lambda '({{B}_{3}})}^{|E({{B}_{3}})|}{m{{'}_{{{B}_{3}}, i}}{{p}^{i}}{{(1-p)}^{|E({{B}_{3}})|-i}}=} \\ &1-9\times {{0.1}^{2}}\times {{0.9}^{4}}-2\times {{0.1}^{3}}\times {{0.9}^{3}}\approx 0.9395 \\ \end{align} $ |
| $ \begin{align} &R'({{R}_{3}}, p)=R'({{R}_{3}}, 0.1)=\\ &1-\sum\limits_{i=\lambda '({{R}_{3}})}^{|E({{R}_{3}})|}{m{{'}_{{{R}_{3}}, i}}{{p}^{i}}{{(1-p)}^{|E({{R}_{3}})|-i}}=} \\ &1-9\times {{0.1}^{4}}\times {{0.9}^{5}}-45\times {{0.1}^{5}}\times {{0.9}^{4}}- \\ &6\times {{0.1}^{6}}\times {{0.9}^{3}}\approx 0.9992 \\ \end{align} $ |
由例1和例2的结果得知,无论在“传统边故障模型”还是“条件边故障模型”下,增广泡型网络R3的可靠性均高于泡型网络B3。即,R3的容错能力高于B3。使用类似方法,分析可知,当n≥3时,n维增广泡型网络的容错能力高于n维泡型网络。
4 结语并行计算机系统底层网络的选择和设计对系统的性能具有决定作用。本文在泡型网络的基础上设计了一款新的网络结构,即增广泡型网络。由于增广泡型网络中包含同维的泡型网络,所以它继承了泡型网络的绝大多数优秀性能,并且可以移植泡型网络的路由算法,模拟泡型网络的行为。同时,由于每个节点按照既定的规律增加1度,使得增广泡型网络具有比泡型网络更好的连通性能和更强的容错能力。当故障发生时,增广泡型网络的容错路由算法,节点之间的信息并发机制,子网保持能力等是值得进一步关注的主要问题。
| [1] | ESFAHANIAN A H, HAKIMI S L. On computing a conditional edge-connectivity of a graph[J]. Information Processing Letters, 1988, 27 (4) : 195-199. doi: 10.1016/0020-0190(88)90025-7 |
| [2] | WANG X, FAN J, ZHOU J, et al. The restricted h-connectivity of the data center network DCell[J]. Discrete Applied Mathematics, 2016, 203 : 144-157. doi: 10.1016/j.dam.2015.09.002 |
| [3] | HSIEH S Y, HUANG H W, LEE C W. {2, 3}-restricted connectivity of locally twisted cubes[J]. Theoretical Computer Science, 2016, 615 : 78-90. doi: 10.1016/j.tcs.2015.11.050 |
| [4] | LIN L, XU L, ZHOU S, et al. The extra, restricted connectivity and conditional diagnosability of split-star networks[J]. IEEE Transactions on Parallel and Disributed Systems, 2016, 27 (2) : 533-545. doi: 10.1109/TPDS.2015.2400459 |
| [5] | LIN R, ZHANG H. The restricted edge-connectivity and restricted connectivity of augmented k-ary n-cubes[J]. International Journal of Computer Mathematics, 2016, 93 (8) : 1281-1298. doi: 10.1080/00207160.2015.1067690 |
| [6] | LI S, TU J, YU C. The generalized 3-connectivity of star graphs and bubble-sort graphs[J]. Applied Mathematics and Computation, 2016, 274 (4) : 41-46. |
| [7] | XU X, XU M, JING J. Edge-fault-tolerant edge-bipancyclicity of bubble-sort graphs[J]. Acta Mathematica Sinica (English Series), 2012, 28 (4) : 675-686. doi: 10.1007/s10114-011-0511-z |
| [8] | WANG J, XU X, GAO L. Decycling bubble sort graphs[J]. Discrete Applied Mathematics, 2015, 194 (C) : 178-182. |
| [9] | WANG S, YANG Y. Fault tolerance in bubble-sort graph networks[J]. Theoretical Computer Science, 2012, 421 (3) : 62-69. |
| [10] | YANG Y, WANG S, LI J. Subnetwork preclusion for bubble-sort networks[J]. Information Processing Letters, 2015, 115 (11) : 817-821. doi: 10.1016/j.ipl.2015.06.011 |
| [11] | CHENG E, LIPTÁK L, SHAWASH N. Orienting Cayley graphs generated by transposition trees[J]. Computers and Mathematics with Applications, 2008, 55 (11) : 2662-2672. doi: 10.1016/j.camwa.2007.10.016 |
| [12] | BONDY J A, MURTY U S R. Graph Theory[M]. New York: Springer, 2008 : 623 -628. |




