2. 四川师范大学 数学与软件科学学院, 成都 610068
2. College of Mathematics and Software Science, Sichuan Normal University, Chengdu Sichuan 610068, China
XIONG Fang, born in 1981, M. S., lecturer. Her research interests include rough set, data mining.
ZHANG Xianyong, born in 1978, Ph. D., associate professor. His research interests include rough set, granular computing, three-way decision.
粗糙集理论是人工智能热点之一, 能够有效处理不精确、不一致、不完整数据。经典定性粗糙集(PawlakRS)[1]具有过拟合局限, 而定量模型更能适应实际噪声环境。概率粗糙集是主流量化模型, 包括变精度粗糙集(Variable Precision Rough Set, VPRS)[2]、决策粗糙集(Decision-Theoretic Rough Set, DTRS)[3]等。其中, VPRS具有错误容忍机制与鲁棒性, 是一种常用定量模型, 文献[4]基于容差关系对其进行了研究。
属性约简是粗糙集理论的核心内容,主要应用于数据分析。模型区域是属性约简构建的基本路线, 其中的分类区域组建于决策区域。对定性PawlakRS,区域具有粒化单调性,因此属性约简主要保持分类正域与保持协调规则[1]。对定量粗糙集, 区域呈现粒化不确定性[5], 定量属性约简成为难点。对定量VPRS, 文献[6]基于近似区域分布构建分布约简, 文献[7]提出约简增量算法处理动态数据, 文献[8]聚焦核并提出最小约简算法。
三支决策是二支决策的理性拓展, 是一种普适性的智能理论[9], 特别适用于粗糙集及其属性约简。文献[10]建立三支决策空间探讨三支决策, 文献[11]基于三支分类区域建立三支决策约简。三支决策紧密联系具有正模式与负模式的二分类, 决策类的正域、负域、边界域对应接受、拒绝、不承诺决策, 成为三支决策区域。三支决策有利于二分类模式识别, 而二分类属性约简则是定量属性约简的有效切入点。对此, 文献[12]研究二分类DTRS的定量约简与层次约简, 并对定量与定性约简进行集成构建。
本文针对二分类VPRS并采用三支决策区域, 构建分类区域保持(Classification-Regions Preservation, CRP)与决策区域保持(Decision-Regions Preservation, DRP)两类定量约简, 分析对PawlakRS定性约简的量化扩张性, 设计区域约简基于核的结构启发算法。进而, 研究DRP约简与CRP约简的强弱关系, 设计由强至弱的结构启发算法, 分析二支决策展向三支决策的约简改进。最后, 依据数据表实例与UCI数据集验证两类区域约简及其关系与算法。
1 三支决策区域本章利用文献[1-2]回顾PawlakRS与VPRS三支决策区域, 以及PawlakRS分类区域。决策表(U, C∪D)中, 设R⊆C, U/R={[x]R}, U/D={[x]D}含决策类X。
PawlakRS中, X的三支决策区域为:
| $\left\{ \begin{align} & PO{{S}_{R}}(X)=\bigcup \{{{[x]}_{R}}:{{[x]}_{R}}\subseteq X\} \\ & NE{{G}_{R}}(X)=\bigcup \{{{[x]}_{R}}:{{[x]}_{R}}\subseteq -X\} \\ & BN{{D}_{R}}(X)=\bigcup \{{{[x]}_{R}}:{{[x]}_{R}}\bigcap X, -X\ne \varnothing \} \\ \end{align} \right.$ | (1) |
VPRS中, 阈值β∈[0, 0.5), 粒[x]R对于X的错误分类率为:c([x]R, X)=1-|[x]R∩X|/|[xR]|;X的三支决策区域为:
| $\left\{ \begin{align} & POS_{R}^{\beta }(X)=\bigcup \{{{[x]}_{R}}:c({{[x]}_{R}}, X)\le \beta \} \\ & NEG_{R}^{\beta }(X)=\bigcup \{{{[x]}_{R}}:c({{[x]}_{R}}, X)\ge 1-\beta \} \\ & BND_{R}^{\beta }(X)=\bigcup \{{{[x]}_{R}}:c({{[x]}_{R}}, X)\in (\beta, 1-\beta )\} \\ \end{align} \right.$ | (2) |
PawlakRS三支决策区域具有粒化单调性。基于β=0, VPRS具有对PawlakRS的扩张性。在量化扩张后, VPRS三支决策区域不再具有粒化单调性[5]。
三支决策区域可以集成构建分类区域。PawlakRS中, 分类正域与分类边界为:
| $\left\{ \begin{align} & PO{{S}_{R}}(D)={{\bigcup }_{X\in U/D}}PO{{S}_{R}}(X) \\ & BN{{D}_{R}}(D)=U-PO{{S}_{R}}(D) \\ \end{align} \right.$ | (3) |
在二分类时(即U/D={X, -X}):
| $PO{{S}_{R}}(D)=PO{{S}_{R}}(X)\bigcup PO{{S}_{R}}(-X)$ | (4) |
针对二分类VPRS, 本章基于三支决策区域来构建分类区域, 进而确立相应保持约简。
定义1 VPRS中, 分类正域与分类边界为:
| $\left\{ \begin{align} & POS_{R}^{\beta }(D)=POS_{R}^{\beta }(X)\bigcup POS_{R}^{\beta }(-X) \\ & BND_{R}^{\beta }(D)=U-POS_{R}^{\beta }(D) \\ \end{align} \right.$ | (5) |
定理1 1)VPRS中, BNDRβ(D)=BNDRβ(X)、POSRβ(D)=POSRβ(X)∪NEGRβ(X);2)PawlakRS中, BNDR(D)=BNDR(X)、POSR(D)=POSR(X)∪NEGR(X)。
定理2 VPRS分类区域扩张了PawlakRS分类区域。
模拟PawlakRS分类区域, 定义1采用决策正域集成构建VPRS分类区域。由于补集正域等于原集负域[1-2], 定理1进而给出VPRS与PawlakRS分类区域的三支决策区域刻画。基于决策区域扩张性及集成构造, 定理2表明分类区域扩张性。相应地, PawlakRS分类区域具有粒化单调性, 而VPRS分类区域不具粒化单调性。
传统属性约简保持分类正域, 即保持分类区域(CRP), 以获取相同分类识别能力。下面研究二分类VPRS的CRP约简。其中, 只需分类正域保持, 并突出PawlakRS定性退化。
定义2 R称为VPRS-CRP约简, 若:
1)POSRβ(D)=POSCβ(D);
2)POSR-{r}β(D)≠POSRβ(D), ∀r∈R。
约简集记为REDCRPβ, 约简核为CORECRPβ=∩REDCRPβ。
定义3 R称为PawlakRS-CRP约简, 若:
1)POSR(D)=POSC(D);
2)POSR-{r}(D)≠POSR(D), ∀r∈R。
约简集记为REDCRP, 约简核为CORECRP=∩REDCRP。
定理3 VPRS-CRP约简扩张了PawlakRS-CRP约简。
VPRS-CRP约简基于错误容忍性, 定量保持确定性决策规则:[x]R→X or -X;PawlakRS-CRP约简基于绝对性, 定性保持确定性决策规则。两种约简分别基于β∈[0, 0.5)与β=0, 具有理论扩张性与实际逼近性。
CRP约简核定义为约简交, 但具有计算公式:
| $\left\{ \begin{align} & CORE_{CRP}^{\beta }=\{c:POS_{C-\{c\}}^{\beta }(D)\ne POS_{C}^{\beta }(D)\} \\ & COR{{E}_{CRP}}=\{c:PO{{S}_{C-\{c\}}}(D)\ne PO{{S}_{C}}(D)\} \\ \end{align} \right.$ | (6) |
这样, 能够用核启发构造CRP约简算法, 下面以计算VPRS-CRP约简为例。
算法1 基于核的VPRS-CRP约简启发算法。
输入 决策表(U, C∪D)与阈值β。
输出 VPRS-CRP约简R∈REDCRPβ。
1)计算核CORECRPβ
2)令R=C
3) FOR r∈R-CORECRPβ DO
4) IF POSR-{r}β(D)=POSRβ(D)
THEN R←R-{r}
5) END IF
6) END FOR
7) Return R
算法1中, CORECRPβ与C界定了VPRS-CRP约简R范围:CORECRPβ⊆R⊆C。步骤1)计算核, 步骤2)从C出发寻找R。步骤3)~6)采用属性删除策略进行搜索, 其中, FOR循环顺序地检查属性r∈R-CORECRPβ, 并通过IF条件进行属性删除判别:若删除r保持分类正域, 则删除r。通过检查所有核外属性, R满足CRP目标且不含冗余属性, 故成为VPRS-CRP约简, 并在步骤7)中输出。算法1是收敛与有效的, 最终获取的约简R依赖于FOR循环顺序。若设置β=0, 算法1则退化为PawlakRS-CRP约简算法。
3 VPRS决策区域保持属性约简第2章的分类区域与CRP约简都关联于三支决策区域。三支决策区域贴近二分类模式, 具有决策根本性, 值得保持以获取规则信息。针对量化区域变迁不确定性[5], 决策区域保持(DRP)变得合理与必要。本章研究VPRS决策区域保持约简(VPRS-DRP)及其定性退化。为此, 引入三维形式的三支决策区域向量:
| $\left\{ \begin{align} & \overrightarrow{3\boldsymbol{REG}}_{R}^{\beta }(X)=\, (POS_{R}^{\beta }(X), BND_{R}^{\beta }(X), NEG_{R}^{\beta }(X)) \\ & {{\overrightarrow{3\boldsymbol{REG}}}_{R}}(X)=\, (PO{{S}_{R}}(X), BN{{D}_{R}}(X), NE{{G}_{R}}(X)) \\ \end{align} \right.$ | (7) |
定义4 R称为VPRS-DRP约简, 若:
1)3REGRβ(X)=3REGCβ(X);
2)3REGR-{r}β(X)≠3REGRβ(X), ∀r∈R。
约简集记为REDDRPβ, 约简核为COREDRPβ=∩REDDRPβ。
定义5 R称为PawlakRS-DRP约简, 若:
1)3REGR(X)=3REGC(X);
2)3REGR-{r}(X)≠3REGR(X), ∀r∈R。
约简集记为REDDRP, 约简核为COREDRP=∩REDDRP。
定理4 VPRS-DRP约简扩张了PawlakRS-DRP约简。
VPRS-DRP约简基于错误容忍性, 定量保持肯定确定性决策规则[x]R→X与否定确定性决策规则[x]R→-X;PawlakRS-DRP约简基于绝对性, 定性保持两者。基于区域扩张性, 两种约简自然具有扩张性。
定理5 VPRS-DRP约简等价于下分布约简。
证明 在二分类情形下, 下分布约简[6]保持目标为:
| $ \begin{align} & ({{\underline{C}}_{\beta }}(X), {{\underline{C}}_{\beta }}(-X))=(POS_{C}^{\beta }(X), POS_{C}^{\beta }(-X))= \\ & (POS_{C}^{\beta }(X), NEG_{C}^{\beta }(X)), \\ \end{align} $ |
其等价于保持3RegCβ(X), 即DRP。进而, 下分布约简等价于DRP约简。 证毕。
除了约简交的定义, DRP约简核还具有计算公式:
| $\left\{ \begin{align} & CORE_{DRP}^{\beta }=\{c:\overrightarrow{3\boldsymbol{REG}}_{C-\{c\}}^{\beta }(X)\ne \overrightarrow{3\boldsymbol{REG}}_{C}^{\beta }(X)\} \\ & COR{{E}_{DRP}}=\{c:{{\overrightarrow{3\boldsymbol{REG}}}_{C-\{c\}}}(X)\ne {{\overrightarrow{3\boldsymbol{REG}}}_{C}}(X)\} \\ \end{align} \right.$ | (8) |
类似算法1, 可以构造DRP约简基于核的结构启发算法。
4 VPRS区域属性约简的强弱关系本章利用属性约简强弱理论[12]分析VPRS-CRP约简(含PawlakRS-CRP约简)与VPRS-DRP约简(含PawlakRS-DRP约简)的强弱关系。
定理6 VPRS-DRP约简强于VPRS-CRP约简, 且:
1)∀R*∈REDDRPβ, ∃R∈REDCRPβ, s.t. R⊆R*;
2)COREDRPβ⊇CORECRPβ。
基于定理6, 每个VPRS-DRP约简R*都能够包含一个VPRS-CRP约简R。从而, 可以设计一个由强至弱的生成算法, 即由一个VPRS-DRP约简内部诱导一个VPRS-CRP约简。相反, VPRS-CRP约简不能启发生成VPRS-DRP约简, 但可以提供一些否定判别。
算法2 基于VPRS-DRP约简的VPRS-CRP约简启发算法。
输入 决策表(U, C∪D)与阈值β, R*∈REDDRPβ。
输出 VPRS-CRP约简R∈REDCRPβ满足R⊆R*。
1)计算核CORECRPβ
2)令R=R*
3) FOR r∈R-CORECRPβ DO
4) IF POSR-{r}β(D)=POSRβ(D)
THEN R←R-{r}
5) END IF
6) END FOR
7) Return R
VPRS-DRP约简R*与核CORECRPβ界定了VPRS-CRP约简R范围:CORECRPβ⊆R⊆R*。算法2类似算法1, 只是从VPRS-DRP约简R*出发(而非从C出发)。算法2采用属性删除策略, 能够基于FOR循环顺序找到一个VPRS-CRP约简, 是有效的结构启发算法。
定理7 PawlakRS-DRP约简等价PawlakRS-CRP约简。
证明 DRP自然诱导CRP; 反之, 设R满足CRP, 即:
POSR(X)∪NEGR(X)=POSC(X)∪NEGC(X)
根据粒化单调性与反证法有:
| $ \left\{ \begin{align} & PO{{S}_{R}}(X)=PO{{S}_{C}}(X) \\ & NE{{G}_{R}}(X)=NE{{G}_{C}}(X) \\ \end{align} \right. $ |
故3REGR(X)=3REGC(X), 即R满足DRP。综上, 约简目标DRP与CRP等价, 故两种约简等价。 证毕。
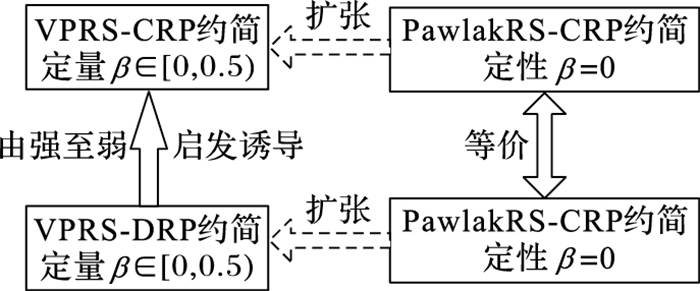
图 1总结了4种约简关系。VPRS-CRP定量约简关联β∈[0, 0.5), 扩张PawlakRS-CRP定性约简; VPRS-DRP定量约简关联β∈[0, 0.5), 扩张PawlakRS-DRP定性约简; VPRS-DRP约简强于并可启发VPRS-CRP约简; PawlakRS-DRP约简等价于PawlakRS-CRP约简。
|
图 1 区域约简及其关系 |
DRP约简具有对CRP约简的改进性, 这得益于三支决策对于二支决策的改进。CRP约简保持二支分类区域, 即保持关联于确定性与不确定性规则的二支决策;DRP约简保持三支决策区域, 即保持关联于肯定确定性、否定确定性与不确定性规则的三支决策,因此, DRP约简针对CRP约简的二支决策进行了三支决策改进, 主要将确定性规则保持细化为肯定与否定确定性规则保持。
5 数据表实例本章用文献[12]中例3数据表进行实例说明。二分类决策表中, U/C={[x]1, [x]2, …, [x]8}, 相关数据信息如表 1所示。
| 表 1 基于C粒的统计数据表 |
这里取β=0.2与β=0来计算VPRS定量约简与PawlakRS定性约简。
1)
| $ \left\{ \begin{align} & POS_{C}^{0.2}(D)=\, \underset{i=1, 2, 3, 6, 7, 8}{\mathop{\bigcup }}\, {{[x]}_{i}} \\ & \overrightarrow{3\boldsymbol{REG}}_{C}^{0.2}(X)=\, (\underset{i=6, 7, 8}{\mathop{\bigcup }}\, {{[x]}_{i}}, \underset{i=4, 5}{\mathop{\bigcup }}\, {{[x]}_{i}}, \underset{i=1, 2, 3}{\mathop{\bigcup }}\, {{[x]}_{i}}) \\ \end{align} \right. $ |
2)
| $ \left\{ \begin{align} & PO{{S}_{C}}(D)=\underset{i=1, 2, 7, 8}{\mathop{\bigcup }}\, \, {{[x]}_{i}} \\ & {{\overrightarrow{3\boldsymbol{REG}}}_{C}}(X)=\, (\underset{i=7, 8}{\mathop{\bigcup }}\, {{[x]}_{i}}, \underset{i=3, 4, 5, 6}{\mathop{\bigcup }}\, {{[x]}_{i}}, \underset{i=1, 2}{\mathop{\bigcup }}\, {{[x]}_{i}}) \\ \end{align} \right. $ |
进而, 表 2提供了4种属性约简及其核的计算结果。
| 表 2 实例的区域属性约简及核 |
对算法1, 从C与空核出发, 需要检查每个属性。按顺序c1→c2→c3→c4, 需依次去除c1、c4, 得到VPRS-CRP约简{c2, c3};如果按c4→c3→c2→c1, 则需依次去除c4、c3、c2, 得到VPRS-CRP约简{c1}。
根据表 2, {c1, c2}, {c1, c3}∈REDDRP0.2、{c1, c2}, {c1, c3}⊇{c1}∈REDCRP0.2、CORESRP0.2={c1}⊇∅=CORECRP0.2, 故验证了定理6所述VPRS-DRP约简与VPRS-CRP约简的强弱关系。
给定VPRS-DRP约简R*={c1, c2}或R*={c1, c3}, 在范围∅⊆R⊆R*中, 算法2能够得到VPRS-CRP约简R={c1}。VPRS-CRP约简{c2, c3}不能由VPRS-DRP约简启发生成。PawlakRS-DRP与PawlakRS-CRP约简是等同的, 这验证了定理7的等价性。
6 UCI数据实验本章选用3个典型的二分类UCI数据集[12]实施数据实验。在表 3中, Monks-3数据集含432个测试对象, 其中的122个训练实例含5%的分类噪声;Voting数据集具有缺损值, 需要错误容忍;Spect-Heart数据集含22个属性元, 具有属性约简的宽泛搜索空间。这3个数据集分别具有噪声不精确、缺损不确定、属性代表性的特征, 适用于本文二分类VPRS属性约简及其定性退化约简的验证。
| 表 3 三个UCI数据集 |
这里, β仍然取0.2与0, X对应数据集第一记录。四类属性约简及核的计算结果如表 4。其中, 1、0表征条件属性选取, 二进制代码及其十进制数值对应条件属性子集。例如, Voting属性子集{c1, c2, c3, c9, c11, c13, c16}对应16位二进制代码1110000010101001及十进制数值57513, 用C57513表示。
| 表 4 属性约简及核的数据实验结果 |
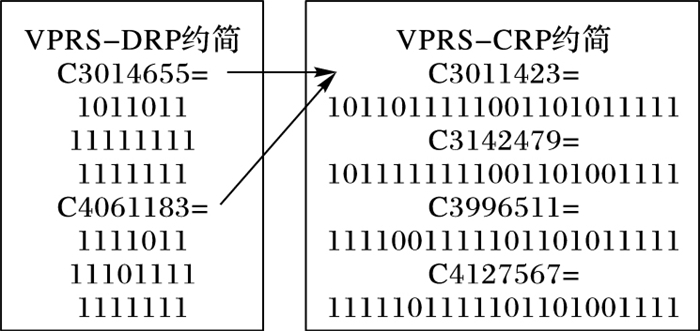
基于表 4, 可以验证VPRS-DRP与VPRS-CRP的强弱约简关系。例如, Spect-Heart数据集具有2个VPRS-DRP约简与4个VPRS-CRP约简, 图 2用箭头标示了约简包含关系。
|
图 2 Spect-Heart中VPRS-DRP约简与VPRS-CRP约简关系 |
基于UCI数据集及其定量/定性约简, 可以提取决策规则建立规则推理库。例如, 针对Voting数据集及β=0.2阈值环境, 利用VPRS-CRP约简C62925=1111010111001101可以建立一个规则库, 其中第一条规则为:
(c1)n(c2)y(c3)n(c4)y(c6)y(c8)n(c9)n(c10)y(c13)y(c14)y(c16)y→drepublican
7 结语本文针对二分类VPRS, 采用三支决策区域, 构建CRP与DRP两类属性约简, 得到强弱性、扩张性、改进性, 并利用双界结构设计区域约简的结构启发算法。CRP约简关联二支决策, DRP约简改进为三支决策, 后者等价于分布约简[6]。区别于文献[12]的集成构建, 本文主要聚焦定量与定性约简的扩张关系与近似逼近。研究结果揭示了二分类VPRS属性约简的强弱关系与优化计算, 保持了确定性与不确定性决策规则, 为多分类数据分析奠定基础。如何泛化拓展研究多分类量化扩张属性约简值得深入探讨, 包括针对VPRS与DTRS等定量模型。
| [1] | PAWLAK Z. Rough sets[J]. International Journal of Information and Computer Science, 1982, 11 (5) : 341-356. doi: 10.1007/BF01001956 |
| [2] | ZIARKO W. Variable precision rough set model[J]. Journal of Computer and System Sciences, 1993, 46 (1) : 39-59. doi: 10.1016/0022-0000(93)90048-2 |
| [3] | YAO Y Y, ZHAO Y. Attribute reduction in decision-theoretic rough set models[J]. Information Sciences, 2008, 178 (17) : 3356-3373. doi: 10.1016/j.ins.2008.05.010 |
| [4] | 徐怡, 李龙澍. 基于(α, λ)联系度容差关系的变精度粗糙集模型[J]. 自动化学报, 2011, 37 (3) : 303-308. ( XU Y, LI L S. Variable precision rough set model based on (α, λ) connection degree tolerance relation[J]. Acta Automatica Sinica, 2011, 37 (3) : 303-308. doi: 10.3724/SP.J.1004.2011.00303 ) |
| [5] | ZHANG X Y, MIAO D Q. Quantitative/qualitative region-change uncertainty/certainty in attribute reduction:comparative region-change analyses based on granular computing[J]. Information Sciences, 2016, 334/335 : 174-204. doi: 10.1016/j.ins.2015.11.037 |
| [6] | MI J S, WU W Z, ZHANG W X. Approaches to knowledge reduction based on variable precision rough set model[J]. Information Sciences, 2004, 159 (3/4) : 255-272. |
| [7] | CHEN D G, YANG Y Y, DONG Z. An incremental algorithm for attribute reduction with variable precision rough sets[J]. Applied Soft Computing, 2016, 45 : 129-149. doi: 10.1016/j.asoc.2016.04.003 |
| [8] | 陈昊, 杨俊安, 庄镇泉. 变精度粗糙集的属性核和最小属性约简算法[J]. 计算机学报, 2012, 35 (5) : 1011-1017. ( CHEN H, YANG J A, ZHUANG Z Q. The core of attributes and minimal attributes reduction in variable precision rough set[J]. Chinese Journal of Computers, 2012, 35 (5) : 1011-1017. doi: 10.3724/SP.J.1016.2012.01011 ) |
| [9] | YAO Y Y. An outline of a theory of three-way decisions[C]//Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing, LNCS 7413. Berlin:Springer, 2012:1-17. http://dx.doi.org/10.1007/978-3-642-32115-3_1 |
| [10] | HU B Q. Three-way decisions space and three-way decisions[J]. Information Sciences, 2014, 281 : 21-52. doi: 10.1016/j.ins.2014.05.015 |
| [11] | CHEN Y M, ZENG Z Q, ZHU Q X, et al. Three-way decision reduction in neighborhood systems[J]. Applied Soft Computing, 2016, 38 : 942-954. doi: 10.1016/j.asoc.2015.10.059 |
| [12] | ZHANG X Y, MIAO D Q. Region-based quantitative and hierarchical attribute reduction in the two-category decision theoretic rough set model[J]. Knowledge-Based Systems, 2014, 71 : 146-161. doi: 10.1016/j.knosys.2014.07.022 |




