0 引言

粗糙集理论^[1]是由波兰学者Pawlak于1982年提出的一种能够有效处理不精确和不确定信息的数学工具, 目前, 由于它在神经网络、数据挖掘、决策分析、机器学习和知识发现等领域^[2-6]有着广泛的运用, 使得研究逐渐趋热。粗糙集理论是建立在分类机制的基础上, 通过等价关系将知识空间进行划分。其主要思想是保持分类能力不变的前提下, 通过上、下近似去刻画知识不确定性程度, 并且通过知识约简、规则提取去挖掘数据中潜在的信息, 粗糙集理论最大的特点就是不需要数据集之外的任何先验信息, 因此对于不确定信息进行分析处理还是比较客观的。近年来, 为了从多粒度、多层次的角度去处理和分析问题, Qian等^[7-9]提出了多粒度粗糙集模型, 其主要思想是将属性集构建成一组属性子集序列, 通过这一系列属性子集来对论域进行划分, 构成了多粒度的论域空间, 然后在多粒度论域空间中对目标概念进行近似逼近。随后, 一些学者在Qian等基础上对多粒度粗糙集做了许多扩展和改进^[10-13]。但是在多粒度粗糙集模型的研究中, 对于如何构建一个较好的属性子集序列, 目前并没有给出一个很好的方法。

本文针对多粒度粗糙集模型中关于属性子集序列的构建问题, 提出一种较好的构建方法, 其主要思想是引入统计学中关于变量间的相似系数来刻画属性间的距离^[14-15], 通过属性间距离的远近来对属性进行区分归类, 进而构建一组属性子集序列。由于目前的多粒度粗糙集模型中分为基于等价关系的多粒度粗糙集模型和邻域多粒度粗糙集模型^[12], 因此本文分别定义了符号型属性间的距离和数值型属性间的距离。最后通过实验分析, 验证了本文构建的属性子集序列具有更好的近似效果。

1 基本理论 1.1 经典粗糙集

假设(U, AT, V, f)为一个信息系统, 其中U为有限对象集合, 也被称为论域, AT为全体属性集, V为全体属性的值域, 其中$V = \mathop \cup \limits_{a \in A} {V_a}$, f为属性到属性值域上的映射, 即f:U×AT→V, f(x, a)∈V_a。若AT=C∪{d}, 其中C为条件属性集, {d}为决策属性集, 则(U, AT=C∪{d}, V, f)被称为决策信息系统。

定义1^[1]  对于信息系统(U, AT, V, f), 设∀B⊆AT, 记：

${R_B} = \{ (x, y)\left| {f(x, {a_k}) = f(y, {a_k}), } \right.\forall {a_k} \in B\} $

(1)

则R_B是U上的等价关系, 所产生对象的等价类为[x]_B={y(x, y)∈R_B}, 因此等价关系R_B在U上产生的划分为:

$U/{R_B} = \{ {[x]_B}\left| {x \in U} \right.\} $

(2)

定义2^[1]  在信息系统(U, AT, V, f)中, 对于∀X⊆U, ∀B⊆AT, 设:

$\underline {{R_B}} X = \cup \{ {[x]_B}\left| {{{[x]}_B} \subseteq X} \right.\} $

(3)

$\overline {{R^B}} X = \cup \{ {[x]_B}\left| {{{[x]}_B} \cap X \ne \emptyset } \right.\} $

(4)

$BN{R_B}X = \overline {{R^B}} X - \underline {{R_B}} X$

(5)

其中：$\underline {{R_B}} X$、$\overline {{R^B}} X$和BNR_BX分别称为X关于B的下近似、上近似和边界。另外称

${{\alpha }_{B}}(X)={\left| \underline{{{R}_{B}}}X \right|}/{\left| \overline{{{R}^{B}}}X \right|}\;$

(6)

为X在属性集B下的近似精度。如果α_B(X)=1, 即上近似与下近似相等, 则称X在信息系统中是可定义的, 否则称X是粗糙的。

1.2 多粒度粗糙集

定义3^[7]  设(U, AT, V, f)是一个信息系统, A₁, A₂, …, a_m为多粒度粗糙集模型下的属性子集序列, 并且满足A₁, A₂, …, a_m⊆AT, 对于∀X⊆U, 则X基于A₁, A₂, …, a_m下的多粒度粗糙集下近似和上近似分别定义为:

$\begin{gathered} \underline {\sum\limits_{i = 1}^m {{A_i}} } X = \{ x \in U\left| {{{[x]}_{{A_1}}} \subseteq X \vee } \right. \hfill \\ {[x]_{{A_2}}} \subseteq X \vee \cdots \vee {[x]_{{A_m}}} \subseteq X\} \hfill \\ \end{gathered} $

(7)

$\overline {\sum\limits_{i = 1}^m {{A_i}} } X = - \underline {\sum\limits_{i = 1}^m {{A_i}} } ( - X)$

(8)

$\left( {\underline {\sum\limits_{i = 1}^m {{A_i}} } X, \overline {\sum\limits_{i = 1}^m {{A_i}} } X} \right)$称为多粒度粗糙集模型。另外称

$\alpha \left( \sum\limits_{i=1}^{m}{{{A}_{i}}},X \right)={\left| \underline{\sum\limits_{i=1}^{m}{{{A}_{i}}}}X \right|}/{\left| \overline{\sum\limits_{i=1}^{m}{{{A}_{i}}}}X \right|}\;$

(9)

为X在$\sum\limits_{i = 1}^m {{A_i}} $下的近似精度。

1.3 邻域多粒度粗糙集

由于经典粗糙集理论只能处理符号型属性, 而无法处理数值型属性。近年来, Hu等^[16-17]和Lin等^[18]运用邻域关系代替等价关系, 提出了邻域粗糙集模型, 使得可以直接处理数值型属性。在此基础上, Lin等^[12]将邻域关系运用在多粒度粗糙集模型中, 提出了邻域多粒度粗糙集模型。

定义4^[16-17]  设(U, AT, f)是一个邻域信息系统, ∀X⊆U, A⊆AT和B⊆AT分别为符号型属性集和数值型属性集, 对象x在属性集A、B和A∪B下的邻域分别定义为:

${\delta _A}(x) = \{ {x_i} \in U\left| {{\Delta _A}(x, {x_i}) = 0} \right.\} $

(10)

${{\delta }_{B}}(x)=\{x{}_{i}\in U\left| {{\Delta }_{B}}(x,{{x}_{i}})\le \delta \right.\}$

(11)

${\delta _{(A \cup B)}}(x) = \{ {x_i} \in U\left| {{\Delta _A}(x, {x_i}) = 0} \right. \wedge {\Delta _B}(x, {x_i}) \leqslant \delta \} $

(12)

其中:Δ_B(x, x_i)表示对象x与对象x_i在属性集B下的距离, δ为对象的邻域半径。

定义5^[12]  设邻域信息系统{U, AT, f}, A⊆AT为符号型属性集, B⊆AT为数值型属性集, A∪B⊆AT为混合型属性集, U/A、U/B和U/(A∪B)分别表示论域上一个划分和两个覆盖, 对于∀X⊆U, 由A和B导出第一类邻域多粒度粗糙集的下近似和上近似分别定义为:

$\underline {(A + B)} X = \{ x \in U\left| {{\delta _A}(x) \subseteq X \vee } \right.{\delta _B}(x) \subseteq X\} $

(13)

$\overline {(A + B)} X = - \underline {(A + B)} ( - X)$

(14)

本文称$(\underline {(A + B)} X, \overline {(A + B)} X)$为第一类邻域多粒度粗糙集模型。另外称

${\alpha _{(A + B)}}(X) = \left| {(\underline {A + B} )X} \right|/\left| {(\overline {A + B} )X} \right|$

(15)

为X在邻域关系A和B下的近似精度。

定义6^[12]  设邻域信息系统{U, AT, f}, A₁, A₂, …, a_m⊆AT为m个符号型属性集, B₁, B₂, …, B_m⊆AT为m个数值型属性集, N₁, N₂, …, N_m是U上m个邻域关系, 其中N_i是由a_i和B_i导出, 对于∀X⊆U, 由N₁, N₂, …, N_m导出的第二类邻域多粒度粗糙集的下近似和上近似分别定义为：

$\underline {\sum\limits_{i = 1}^m {{N_i}} } X = \cup \{ x \in U\left| {{\delta _{({A_i} + {B_i})}}(x) \subseteq X;} \right.1 \leqslant i \leqslant m\} $

(16)

$\overline {\sum\limits_{i = 1}^m {{N_i}} } X = - \underline {\sum\limits_{i = 1}^m {{N_i}} } ( - X)$

(17)

其中${\delta _{({A_i} + {B_i})}}(x) = \{ x \in U\left| {{\delta _{{A_i}}}(x) \leqslant \delta \vee } \right.{\delta _{{B_i}}}(x) \leqslant \delta \} .$。本文称$\left( {\underline {\sum\limits_{i = 1}^m {{N_i}} } X, \overline {\sum\limits_{i = 1}^m {{N_i}} } X} \right)$为基于m个邻域关系的第二类邻域多粒度粗糙集。另外称

$\alpha \left( \sum\limits_{i=1}^{m}{{{N}_{i}},X} \right)={\left| \underline{\sum\limits_{i=1}^{m}{{{N}_{i}}}}X \right|}/{\left| \overline{\sum\limits_{i=1}^{m}{{{N}_{i}}}}X \right|}\;$

(18)

为X在邻域关系$\sum\limits_{i = 1}^m {{N_i}} $下的近似精度。

2 多粒度粗糙集模型下属性子集序列的构造

多粒度粗糙集模型中, 不同的属性子集序列对于对象集的近似和和决策规则的提取都有着很大的影响, 因此构建合适的属性子集序列具有很重要的意义。

定义7  设信息系统(U, AT, V, f), 其中：U为非空有限对象集且U=n; AT为属性集; V为属性的值域, $V = \mathop \cup \limits_{a \in A} {V_a}$; f为属性到属性值域上的映射, 即f(x, a)∈V_a。对于AT中两个属性a_i, a_j, 若这两个属性均为数值型属性, 定义属性间的距离为:

$\begin{gathered} d({a_i}, {a_j}) = 1 - \hfill \\ \left| {\frac{{\sum\limits_{t = 1}^n {(f({x_t}, {a_i}) - \overline {f(x, {a_i})} )(f({x_t}, {a_j}) - \overline {f(x, {a_j})} )} }}{{\sqrt {\sum\limits_{t = 1}^n {{{(f({x_t}, {a_i}) - \overline {f(x, {a_i})} )}^2}} } \sqrt {\sum\limits_{t = 1}^n {{{(f({x_t}, {a_j}) - \overline {f(x, {a_j})} )}^2}} } }}} \right| \hfill \\ \end{gathered} $

(19)

其中:x_t∈U; $\overline {f(x, {a_i})}, \overline {f(x, {a_j})} $分别表示a_i、a_j下所有对象属性值的平均值。这里可以容易证明d(a_i, a_j)∈[0, 1]。

若这两个属性均为符号型属性, 设属性a_i的p种取值记为r₁, r₂, …, r_p；属性a_j的q种取值记为t₁, t₂, …, t_q, n个对象在属性a_i, a_j下的属性值经过整理后列成表 1, 此表又被称为列联表, 其中n_kl表示在n个对象中属性a_i取第k个值r_k, 且属性a_j取第l个值t_l的频数。

根据表 1, 定义属性间的距离为：

$d({a_i}, {a_j}) = 1 - \sqrt {\frac{{\chi _{ij}^2}}{{{n_{ + + }} \times \min [(p-1), (q-1)]}}}, $

(20)

其中$\chi _{ij}^2 = {n_{ + + }}\left( {\sum\limits_{k = 1}^p {\sum\limits_{l = 1}^q {\frac{{n_{kl}^2}}{{{n_{k + }}{n_{ + l}}}} - 1} } } \right)$, 即这两个符号型属性独立性检验中的χ²统计量^[14]。这里满足d(a_i, a_j)∈[0, 1]。

根据定义7, 可以得出信息系统中任意两个同类型属性之间的距离, 因此基于属性间距离的大小, 本文可以构建一个多粒度属性子集序列。

定义8  设信息系统(U, AT, V, f), 其中: U为非空有限对象集; AT为属性集且AT=N; V为属性的值域。这里定义多粒度粗糙集模型下属性子集序列为{B₁, B₂, …, B_N}, 其中B₁, B₂, …, B_N⊆AT, 且满足B_i={a∈A|d(a_i, a)≤λ}(1≤i≤N), B_i称为a_i的邻域属性集, λ为属性邻域半径, 是事先给定的一个常数。

从定义8可以看出, 本文构造的多粒度属性子集序列是将属性之间距离较小的属性归类成一组, 由于数据集之间的差异, 这里无法给出具体的邻域半径取值, 但是通常可以取。由于属性间的距离是根据统计学中变量之间相似系数^[14]得来, 因此通过这种方法构造出的多粒度属性子集序列, 其每个属性子集内的属性之间依赖程度较高, 这样更具一定的合理性。最终构建的属性子集序列形成的是属性全集上的一个覆盖。为了验证本文构造的属性子集序列更为优越, 下面将通过实验来具体分析。

3 实验分析

为了验证本文方法性能, 这里从UCI Machine Learning Repository获取了4个数据集进行实验分析和评估。具体信息描述如表 2所示。

在表 2中, 编号为1、3和4的数据集属性均为数值型属性, 编号为2的数据集属性为符号型属性。根据定义7中属性间距离的定义方式, 这里可以得出4个数据集属性间的距离矩阵, 其分别表示为:

$ A = \left[{\begin{array}{*{20}{c}} {0.0}&{0.89}&{0.13}&{0.18} \\ {0.89}&{0.0}&{0.58}&{0.64} \\ {0.13}&{0.58}&{0.0}&{0.04} \\ {0.18}&{0.64}&{0.04}&{0.0} \end{array}} \right] $

$ B = \left[{\begin{array}{*{20}{c}} {0.0}&{1.0}&{1.0}&{1.0} \\ {1.0}&{0.0}&{1.0}&{1.0} \\ {1.0}&{1.0}&{0.0}&{0.8} \\ {1.0}&{1.0}&{0.8}&{0.0} \end{array}} \right] $

$ C = \left[{\begin{array}{*{20}{c}} {0.0}&{0.55}&{0.85}&{0.93}&{0.78}&{0.60}&{0.83} \\ {0.55}&{0.0}&{0.96}&{0.98}&{0.93}&{0.83}&{0.88} \\ {0.85}&{0.96}&{0.0}&{0.69}&{0.93}&{0.90}&{0.94} \\ {0.93}&{0.98}&{0.69}&{0.0}&{0.96}&{0.99}&{0.94} \\ {0.78}&{0.93}&{0.93}&{0.96}&{0.0}&{0.72}&{0.75} \\ {0.60}&{0.83}&{0.90}&{0.99}&{0.72}&{0.0}&{0.19} \\ {0.83}&{0.88}&{0.94}&{0.94}&{0.75}&{0.19}&{0.0} \end{array}} \right] $

$ D = \left[{\begin{array}{*{20}{c}} {0.0}&{0.90}&{0.79}&{0.69}&{0.73}&{0.71}&{0.76}&{0.84}&{0.86}&{0.45}&{0.93}&{0.93}&{0.36} \\ {0.90}&{0.0}&{{\text{0}}{\text{.83}}}&{{\text{0}}{\text{.71}}}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.66}}}&{{\text{0}}{\text{.58}}}&{{\text{0}}{\text{.70}}}&{{\text{0}}{\text{.77}}}&{{\text{0}}{\text{.75}}}&{{\text{0}}{\text{.43}}}&{{\text{0}}{\text{.63}}}&{{\text{0}}{\text{.80}}} \\ {0.79}&{0.83}&{0.0}&{{\text{0}}{\text{.55}}}&{{\text{0}}{\text{.71}}}&{{\text{0}}{\text{.87}}}&{{\text{0}}{\text{.88}}}&{{\text{0}}{\text{.81}}}&{{\text{0}}{\text{.99}}}&{{\text{0}}{\text{.74}}}&{{\text{0}}{\text{.92}}}&{{\text{0}}{\text{.99}}}&{{\text{0}}{\text{.77}}} \\ {0.69}&{0.71}&{{\text{0}}{\text{.55}}}&{0.0}&{{\text{0}}{\text{.91}}}&{{\text{0}}{\text{.67}}}&{{\text{0}}{\text{.64}}}&{{\text{0}}{\text{.63}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.98}}}&{{\text{0}}{\text{.72}}}&{{\text{0}}{\text{.72}}}&{{\text{0}}{\text{.55}}} \\ {0.73}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.71}}}&{{\text{0}}{\text{.91}}}&{0.0}&{{\text{0}}{\text{.78}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.74}}}&{{\text{0}}{\text{.76}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.93}}}&{{\text{0}}{\text{.60}}} \\ {0.71}&{{\text{0}}{\text{.66}}}&{{\text{0}}{\text{.87}}}&{{\text{0}}{\text{.67}}}&{{\text{0}}{\text{.78}}}&{0.0}&{{\text{0}}{\text{.13}}}&{{\text{0}}{\text{.55}}}&{{\text{0}}{\text{.38}}}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.56}}}&{{\text{0}}{\text{.30}}}&{{\text{0}}{\text{.50}}} \\ {0.76}&{{\text{0}}{\text{.58}}}&{{\text{0}}{\text{.88}}}&{{\text{0}}{\text{.64}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.13}}}&{0.0}&{{\text{0}}{\text{.46}}}&{{\text{0}}{\text{.34}}}&{{\text{0}}{\text{.82}}}&{{\text{0}}{\text{.45}}}&{{\text{0}}{\text{.21}}}&{{\text{0}}{\text{.50}}} \\ {0.84}&{{\text{0}}{\text{.70}}}&{{\text{0}}{\text{.81}}}&{{\text{0}}{\text{.63}}}&{{\text{0}}{\text{.74}}}&{{\text{0}}{\text{.55}}}&{{\text{0}}{\text{.46}}}&{0.0}&{{\text{0}}{\text{.63}}}&{{\text{0}}{\text{.86}}}&{{\text{0}}{\text{.73}}}&{{\text{0}}{\text{.49}}}&{{\text{0}}{\text{.68}}} \\ {0.86}&{{\text{0}}{\text{.77}}}&{{\text{0}}{\text{.99}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.76}}}&{{\text{0}}{\text{.38}}}&{{\text{0}}{\text{.34}}}&{{\text{0}}{\text{.63}}}&{0.0}&{{\text{0}}{\text{.97}}}&{{\text{0}}{\text{.70}}}&{{\text{0}}{\text{.48}}}&{{\text{0}}{\text{.66}}} \\ {0.45}&{{\text{0}}{\text{.75}}}&{{\text{0}}{\text{.74}}}&{{\text{0}}{\text{.98}}}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.82}}}&{{\text{0}}{\text{.86}}}&{{\text{0}}{\text{.97}}}&{0.0}&{{\text{0}}{\text{.47}}}&{{\text{0}}{\text{.57}}}&{{\text{0}}{\text{.68}}} \\ {0.93}&{{\text{0}}{\text{.43}}}&{{\text{0}}{\text{.92}}}&{{\text{0}}{\text{.72}}}&{{\text{0}}{\text{.94}}}&{{\text{0}}{\text{.56}}}&{{\text{0}}{\text{.45}}}&{{\text{0}}{\text{.73}}}&{{\text{0}}{\text{.70}}}&{{\text{0}}{\text{.47}}}&{0.0}&{{\text{0}}{\text{.43}}}&{{\text{0}}{\text{.76}}} \\ {0.93}&{{\text{0}}{\text{.63}}}&{{\text{0}}{\text{.99}}}&{{\text{0}}{\text{.72}}}&{{\text{0}}{\text{.93}}}&{{\text{0}}{\text{.30}}}&{{\text{0}}{\text{.21}}}&{{\text{0}}{\text{.49}}}&{{\text{0}}{\text{.48}}}&{{\text{0}}{\text{.57}}}&{{\text{0}}{\text{.43}}}&{0.0}&{{\text{0}}{\text{.68}}} \\ {0.36}&{{\text{0}}{\text{.80}}}&{{\text{0}}{\text{.77}}}&{{\text{0}}{\text{.55}}}&{{\text{0}}{\text{.60}}}&{{\text{0}}{\text{.50}}}&{{\text{0}}{\text{.50}}}&{{\text{0}}{\text{.68}}}&{{\text{0}}{\text{.66}}}&{{\text{0}}{\text{.68}}}&{{\text{0}}{\text{.76}}}&{{\text{0}}{\text{.68}}}&{0.0} \end{array}} \right] $

矩阵A、B、C、D分别表示1~4号数据集的属性间距离矩阵, 即矩阵中第i行第j列的数值为数据集中第i个属性与第j个属性间的距离，因此, 属性间距离矩阵是一个对称矩阵。

接下来, 根据本文提出的多粒度属性子集序列的构造方法, 可以得到各个数据集构造出的属性子集序列, 其分别为：

1){{a₁}, {a₂}, {a₃, a₄}}；

2){{a₁}, {a₂}, {a₃, a₄}}；

3){{a₁}, {a₂}, {a₃}, {a₄}, {a₅}, {a₆, a₇}}；

4){{a₁, a₁₃}, {a₂}, {a₃}, {a₄}, {a₅}, {a₆, a₇, a₉, a₁₂}, {a₈}, {a₆, a₇, a₉}, {a₁₀}, {a₁₁}, {a₆, a₇, a₁₂}}。

由于各个数据集中属性间距离值存在差异, 这里每个数据集的属性邻域半径λ取值也不同, 其中, 数据集1的λ=0.1, 数据集2为λ=0.8, 数据集3为λ=0.2, 数据集4为λ=0.4。

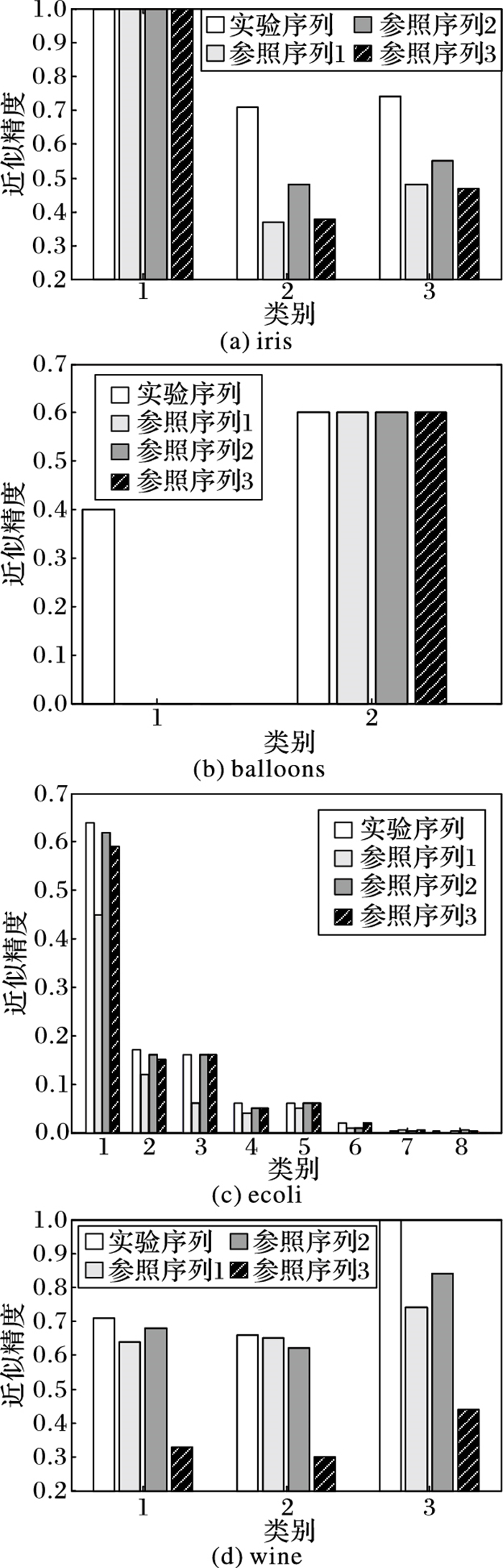
对于数据集中的每个类, 分别计算出它们在构造的属性子集序列下多粒度粗糙集模型中的近似精度。为了作对比, 本实验另外随机构造了3个属性子集序列作为参照, 并且计算出每个类在各个参照序列下的近似精度。最终每个数据集的实验结果如图 1所示。

由于数据集1、3和4属性均为数值型, 因此计算的为每个类在邻域多粒度粗糙集模型下的近似精度。

通过实验结果可以看出, 对于数据集中每个类, 本文方法构造出的属性子集序列(即实验序列)相对于随机生成的参照序列, 其近似精度均更高一点，因此, 本文方法构造出的属性子集序列在其多粒度粗糙集模型的近似方面具有一定的优越性。

4 结语

针对目前多粒度粗糙集模型中属性子集序列的构造问题, 本文通过引入属性间距离函数的方法, 定量地刻画了属性之间距离的远近, 并将距离较近的属性归为一类, 从而构造出一组多粒度属性子集序列。通过实例分析可以看出, 本文中构造出的属性子集序列在其近似对象的近似计算方面具有更高的精度。由于本文未给出属性邻域半径λ的选取方法, 因此在接下来的工作中需要探索如何去选取合适的属性邻域半径。